Содержание
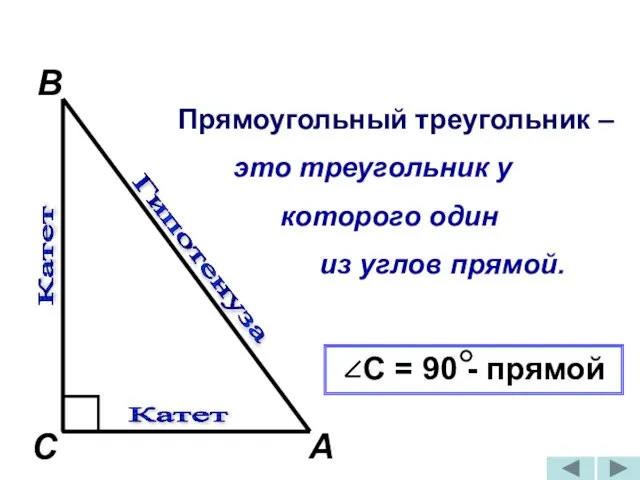
- 2. Катет Гипотенуза Прямоугольный треугольник – это треугольник у которого один из углов прямой. С = 90
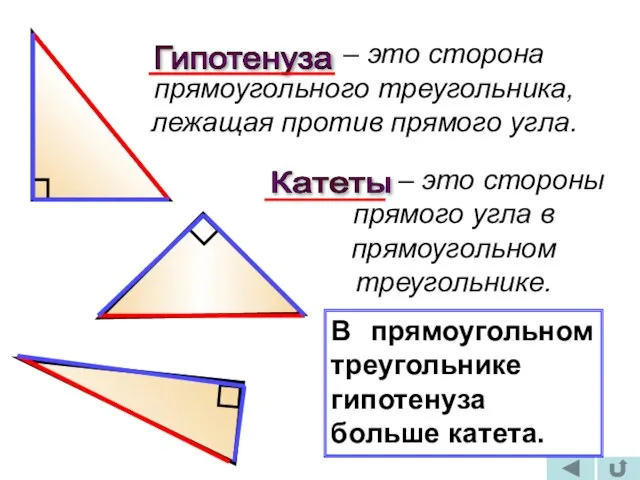
- 3. – это сторона прямоугольного треугольника, лежащая против прямого угла. Гипотенуза – это стороны прямого угла в
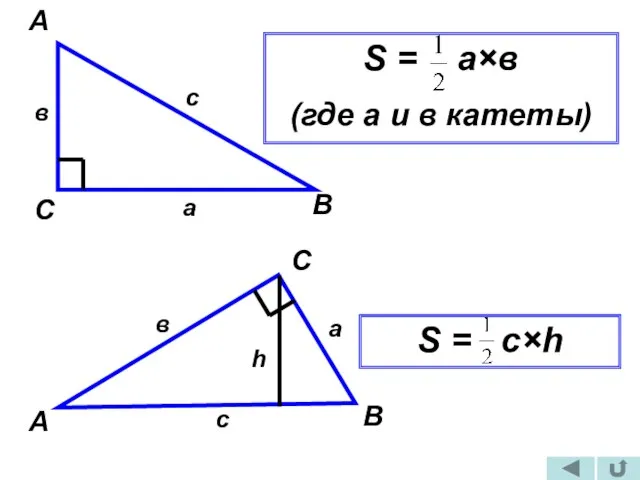
- 4. А В С в а с S = а×в (где а и в катеты) А С
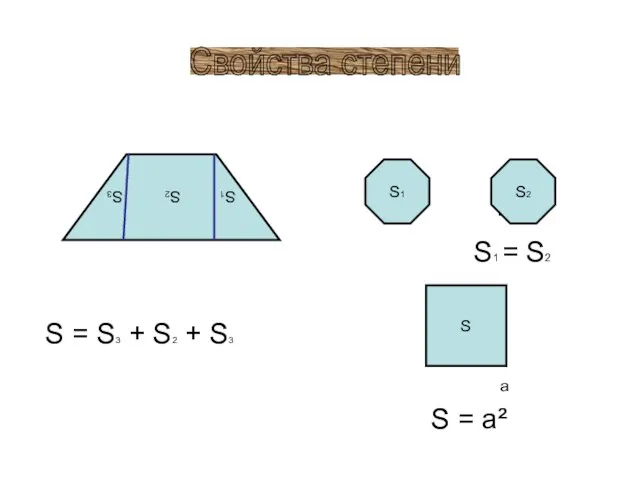
- 5. S = S3 + S2 + S3 = S1 = S2 a a S = a²
- 6. Пифагор Самосский – философ, математик, религиозный и политический деятель, родился в VI веке до н.э. в
- 7. В Южной Италии- г.Кротоне, Пифагор стал таким знаменитым, сделал свои открытия, основал Пифагорейскую школу, в которой
- 8. В научных достижениях Пифагор прославился своей теоремой «в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов»,
- 9. Смерть Пифагора тоже окутана тайной, потому что достоверно сказать, как именно умер Пифагор, невозможно. Одни говорят,
- 10. Есть и еще одна версия, в которой говорится о том, что Пифагор был убит в уличной
- 11. Интересна история теоремы Пифагора. Хотя эта теорема и связывается с именем Пифагора, она была известна задолго
- 12. Сохранилось древнее предание, что в честь своего открытия Пифагор принёс в жертву богам быка, по другим
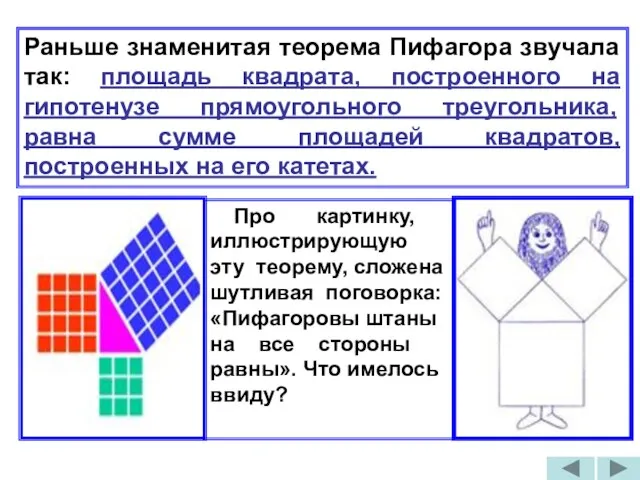
- 13. Раньше знаменитая теорема Пифагора звучала так: площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей
- 14. Теореме Пифагора можно дать эквивалентную формулировку, применив понятие равносоставленных фигур. Попробуем сформулировать теорему Пифагора по другому:
- 15. Тогда площадь квадрата, построенного на гипотенузе – это квадрат гипотенузы, а площади квадратов, построенных на катетах
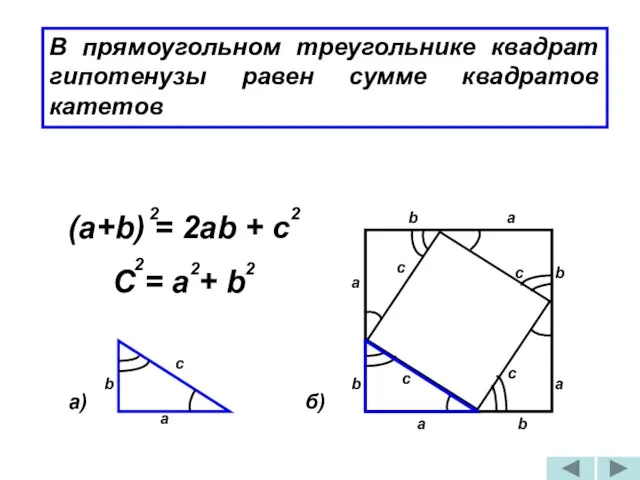
- 16. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов c b a a c b a
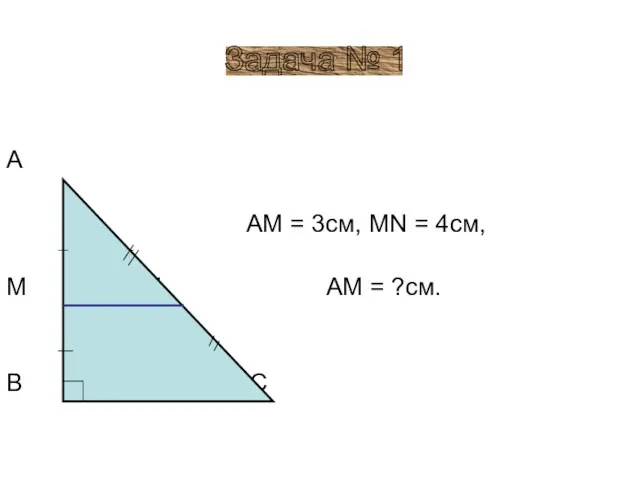
- 17. А AM = 3см, MN = 4см, М N AM = ?см. В C Задача №
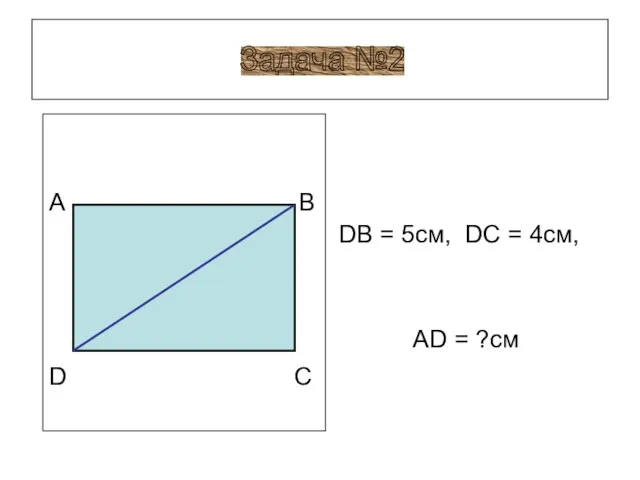
- 18. DB = 5см, DC = 4см, AD = ?см Задача №2 A B D C
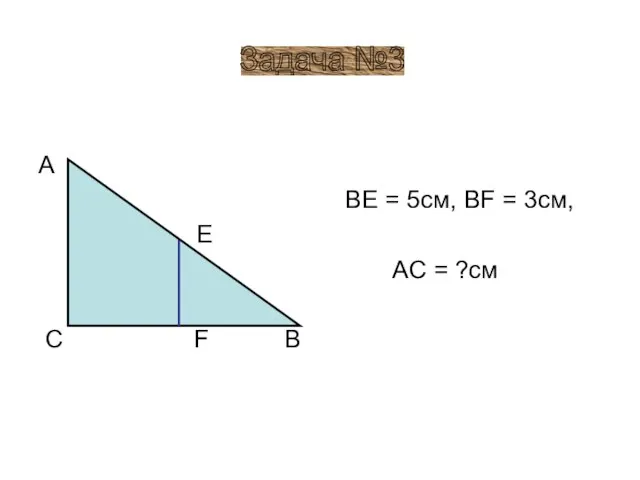
- 19. A E C F B BE = 5см, BF = 3см, AC = ?см Задача №3
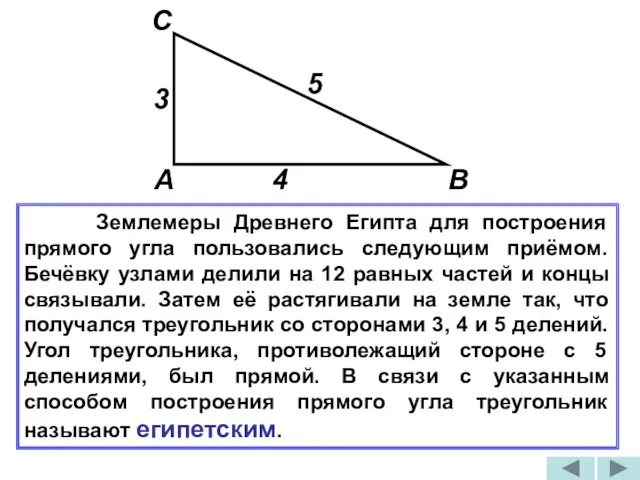
- 20. Землемеры Древнего Египта для построения прямого угла пользовались следующим приёмом. Бечёвку узлами делили на 12 равных
- 21. Пифагоровы треугольники – это прямоугольные треугольники, у которых длины сторон выражаются целыми числами Катеты а, b
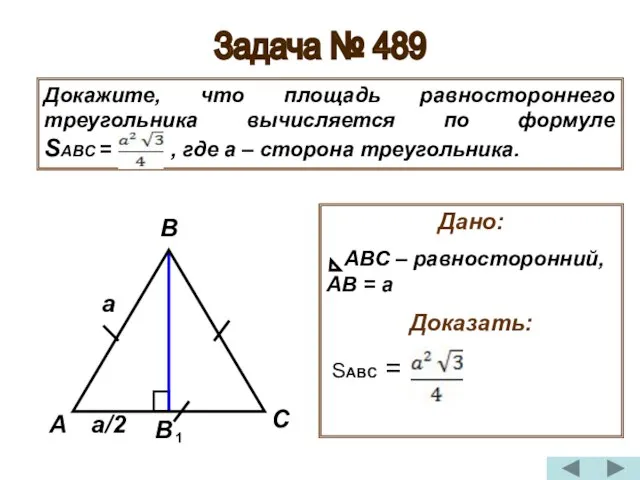
- 22. Задача № 489 Докажите, что площадь равностороннего треугольника вычисляется по формуле SABC = , где а
- 23. Доказательство: 1) Проведём высоту ВВ , тогда АВВ и СВВ - прямоугольные 2) Т.к. АВВ -
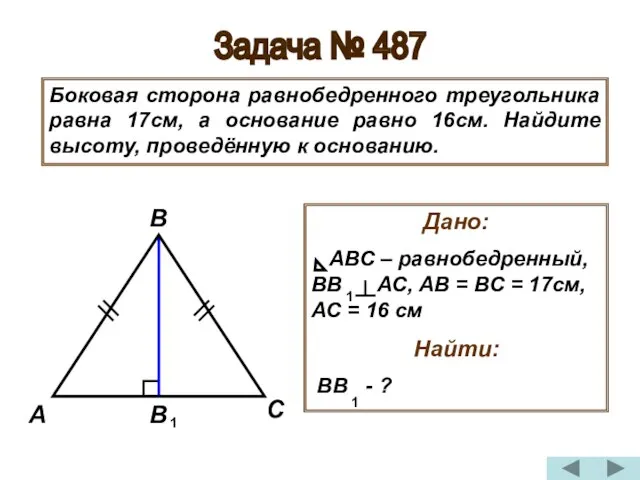
- 24. Задача № 487 Боковая сторона равнобедренного треугольника равна 17см, а основание равно 16см. Найдите высоту, проведённую
- 25. Решение: 1) Известно, что высота, проведённая к основанию равнобедренного треугольника, является медианой, следовательно, АВ =В С=8см
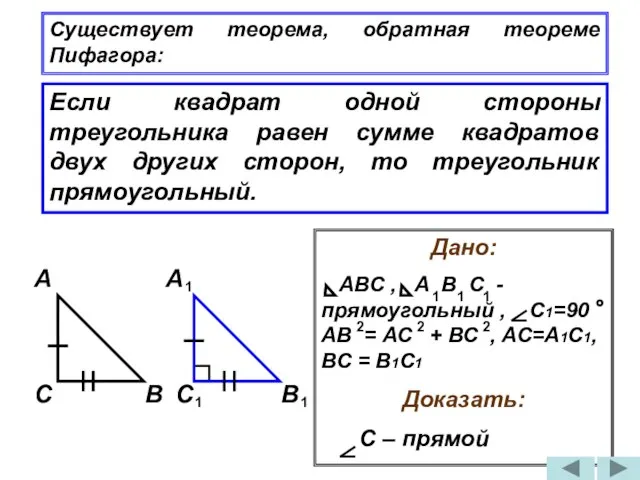
- 26. Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный. Существует теорема,
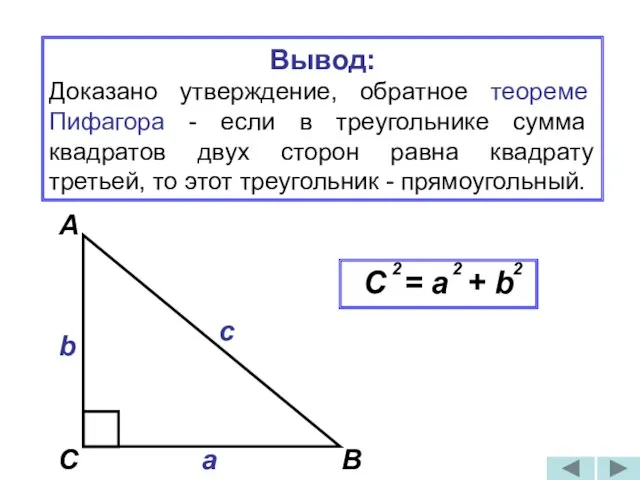
- 27. Вывод: Доказано утверждение, обратное теореме Пифагора - если в треугольнике сумма квадратов двух сторон равна квадрату
- 28. 1. п.п.54, 55 Доказательство теоремы Пифагора и ей обратной. №493. Найти и разобрать другие доказательства теоремы
- 30. Скачать презентацию













 Психология образования
Психология образования Ежегодный отчёт директора школы по итогам 2011-2012 учебного года
Ежегодный отчёт директора школы по итогам 2011-2012 учебного года Типы экологических взаимодействий
Типы экологических взаимодействий Урок « На севере Европы»
Урок « На севере Европы» Риторическая компетенция как ведущее средство образования
Риторическая компетенция как ведущее средство образования Знаки приоритета
Знаки приоритета Примеры речевых форм эмоциональной экспрессии
Примеры речевых форм эмоциональной экспрессии Компьютерный подбор краски для автомобилей. Заправка аэрозольных баллонов краской. Подбор автоэмалей для ремонта царапин
Компьютерный подбор краски для автомобилей. Заправка аэрозольных баллонов краской. Подбор автоэмалей для ремонта царапин Презентация на тему Пути достижения биологического прогресса
Презентация на тему Пути достижения биологического прогресса  Адаптированная примерная основная образовательная программа для дошкольников
Адаптированная примерная основная образовательная программа для дошкольников  Электронные библиотеки и библиотеки: на пути к совершенным интеллектуальным поисковым системам Шрайберг Яков Леонидович, докто
Электронные библиотеки и библиотеки: на пути к совершенным интеллектуальным поисковым системам Шрайберг Яков Леонидович, докто Мексиканский медичи. Евгенио Лопез Алоносо
Мексиканский медичи. Евгенио Лопез Алоносо Важность инновационных продуктов в создании стоимости и качества активов в аптечном секторе
Важность инновационных продуктов в создании стоимости и качества активов в аптечном секторе Слово как культурообразующая сила. Князь Андрей Боголюбский и культурно-историческая среда
Слово как культурообразующая сила. Князь Андрей Боголюбский и культурно-историческая среда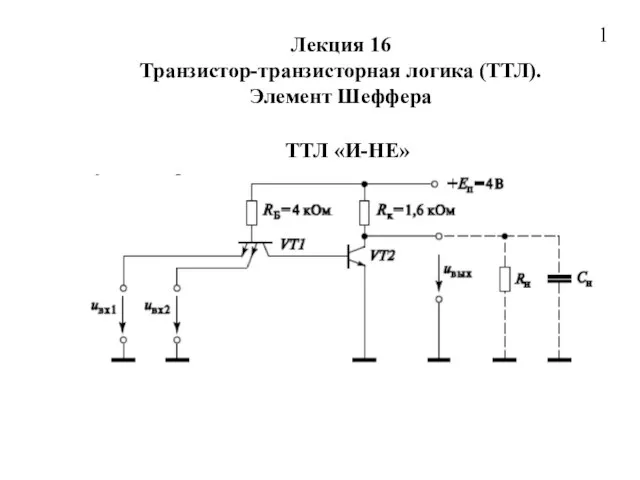 Элемент Шеффера
Элемент Шеффера  Информация об Ассоциации «Рекламная Федерация Регионов»
Информация об Ассоциации «Рекламная Федерация Регионов» Zhivoy_personazh_i_ego_arka
Zhivoy_personazh_i_ego_arka Методы проведения дискуссии
Методы проведения дискуссии  Погоны ВС РФ
Погоны ВС РФ Яндекс_Лавка
Яндекс_Лавка Культурное пространство империи первой половины XIX в
Культурное пространство империи первой половины XIX в Teacher’s Day
Teacher’s Day Знаки +,=,-
Знаки +,=,- Штукатурки цементные ВОЛМА
Штукатурки цементные ВОЛМА Податкові послуги на порталі Дія
Податкові послуги на порталі Дія Метод линейного сплайна
Метод линейного сплайна Механические колебания и волны
Механические колебания и волны Презентация на тему Разделка рыбы
Презентация на тему Разделка рыбы