Содержание
- 2. Смирнова Татьяна Григорьевна Смирнова Татьяна Григорьевна Учитель математики, завуч школы №516
- 3. Теорема Пифагора Теорема Пифагора Формулировка теоремы Проверь себя Задачи с практическим содержанием Задачи Древнего Китая
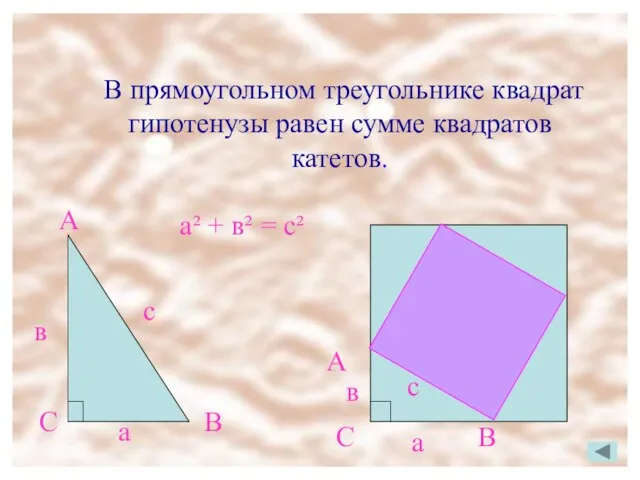
- 4. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. В прямоугольном треугольнике квадрат гипотенузы равен сумме
- 5. Задачи с практическим содержанием Задачи с практическим содержанием 1. Лестница длиной 13 метров приставлена к стене
- 6. 2. Для установки мачты телевизионной антенны изготовлены тросы длиной 17 метров. Тросы крепятся на мачте на
- 7. 3. Вертикальная мачта поддерживается четырьмя канатами, прикрепленными к ней на расстоянии 16 метров от земли и
- 8. 4. Длина маятника АМ=1 м, высота его подъема при отклонении в точку В на некоторый угол
- 9. Задачи Древнего Китая Задачи Древнего Китая Наиболее ранние из дошедших до нас китайских математических текстов относятся
- 10. Имеется водоем со стороной в 1 чжан (=10 чи). В центре его растет камыш, который выступает
- 11. Имеется бамбук высотой в 1 чжан (=10 чи). Вершину его согнули так, что она касается земли
- 13. Скачать презентацию









 Научно Производственное Предприятие «СФЕРА БЕЗОПАСНОСТИ»
Научно Производственное Предприятие «СФЕРА БЕЗОПАСНОСТИ» Мой город Лениногорск
Мой город Лениногорск Интерьер русской избы
Интерьер русской избы 2
2 Искусство страны восходящего солнца
Искусство страны восходящего солнца Гигиена труда
Гигиена труда Транспортное обеспечение внешнеэкономической деятельности
Транспортное обеспечение внешнеэкономической деятельности Необычное применение нефти
Необычное применение нефти PROдвижение
PROдвижение «Тропинка, кочки, копна»
«Тропинка, кочки, копна» Wedding Day Vocabulary
Wedding Day Vocabulary Создание и укрепление Московского государства
Создание и укрепление Московского государства Презентация на тему Техническое регулирование
Презентация на тему Техническое регулирование Правописание -тся и -ться в глаголах
Правописание -тся и -ться в глаголах Презентация на тему Международные валютные рынки и риски
Презентация на тему Международные валютные рынки и риски Геометрические параметры сварного шва
Геометрические параметры сварного шва Объем пирамиды
Объем пирамиды Системы OSS:история и современность
Системы OSS:история и современность Zhestikulyatsia_pri_obschenii
Zhestikulyatsia_pri_obschenii Psikhologia_Avtosokhranenny
Psikhologia_Avtosokhranenny Презентация на тему Культуры Древнего мира
Презентация на тему Культуры Древнего мира  «Amore Mio» Москва. Московская область
«Amore Mio» Москва. Московская область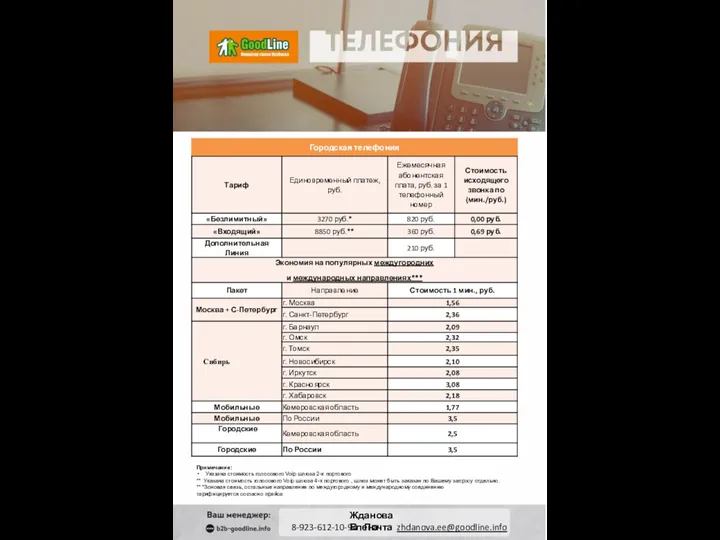 Городская телефония
Городская телефония Боевая гордость Усть-Лабинского района
Боевая гордость Усть-Лабинского района Управление нетворкингом
Управление нетворкингом Интеграция платежных систем с интернет-магазином
Интеграция платежных систем с интернет-магазином Краудфантинг
Краудфантинг АНТАРКТИДА В ЦИФРАХ
АНТАРКТИДА В ЦИФРАХ