Содержание
- 2. Теоретический материал
- 3. Содержание 1) Область определения функции 2) Свойства функции (четность, нечетность, периодичность) 4) Точки пересечения функции с
- 4. Область определения функции Определение. Областью определения функции называется множество значений независимой переменной, при которых функция определена.
- 5. Четные и нечетные функции Функция y=f(x) называется четной, если Функция y=f(x) называется нечетной, если
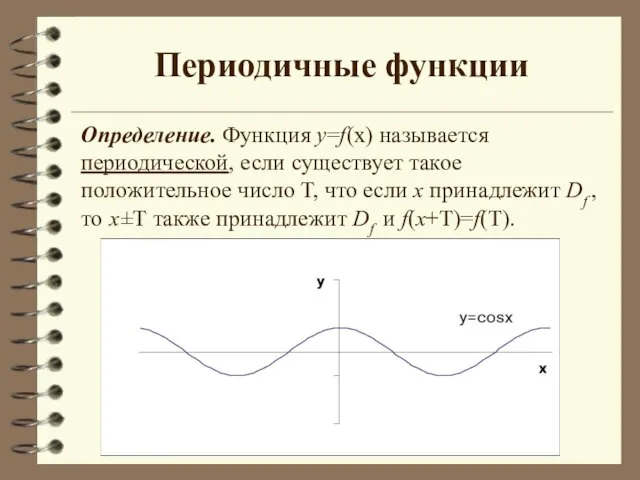
- 6. Периодичные функции Определение. Функция y=f(x) называется периодической, если существует такое положительное число Т, что если х
- 7. Точки пересечения с осями координат При исследовании функции необходимо найти координаты точек пересечения графика функции с
- 8. Непрерывность Характер точек разрыва Функция у=f(x) называется непрерывной в точке х0, если функция определена в точке
- 9. Точки разрыва функции Определение. Точкой разрыва функции называется точка из области определения функции, в которой функция
- 10. Классификация точек разрыва Точки устранимого разрыва Если в точке х0 существуют конечные односторонние пределы функции, равные
- 11. Классификация точек разрыва Точки скачка Если в точке х0 существуют конечные односторонние пределы функции, не равные
- 12. Классификация точек разрыва Точки разрыва II рода Если хотя бы один из односторонних пределов функции в
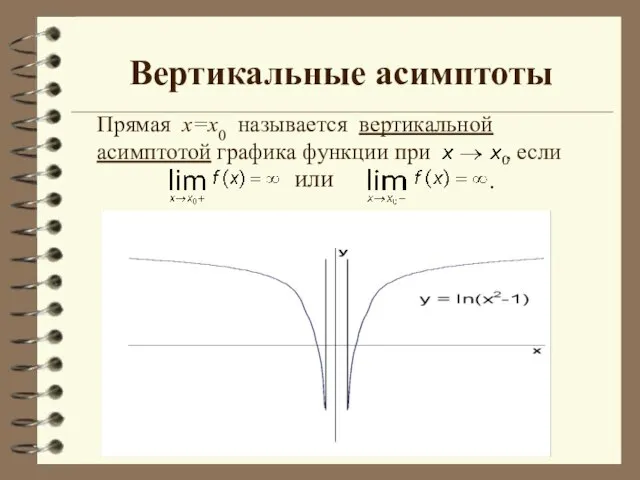
- 13. Вертикальные асимптоты Прямая х=х0 называется вертикальной асимптотой графика функции при , если или .
- 14. Наклонные асимптоты Если существует прямая y=kx+b такая, что , то эта прямая называется асимптотой графика функции
- 15. Экстремумы функции Пусть функция f (x) определена и непрерывна на интервале (а, b). Точка х0 интервала
- 16. Исследование функции на монотонность Критические точки функции х=±1. f '(x)>0 при х 1; f '(x) функция
- 17. Выпуклость функции Функция у=f(х), определенная на интервале (а, b), называется выпуклой вверх (вниз) в интервале (а,
- 18. Выпуклость функции. Точки перегиба Если график функции в точке (х0, f(x0)) переходит с одной стороны касательной
- 19. Достаточные условия выпуклости функции и существования точек перегиба Достаточное условие строгой выпуклости функции Если на интервале
- 20. Практический материал
- 21. Исследуем функцию и построим её график. 1). Поскольку знаменатель положителен при всех , область определения функции
- 22. 4). Найдём наклонные асимптоты при в виде . Имеем: Таким образом, асимптотой как при , так
- 23. 5). Найдём точки пересечения с осями координат. Имеем: f(0) = 0, причём x=0 - единственное решение
- 24. 6) Найдём производную: Очевидно, что f´(x) ≥ 0 при всех ; единственная точка, в которой f´(x)
- 25. 7) Найдём вторую производную: Знаменатель этой дроби положителен при всех x. Числитель имеет корни x=0 и
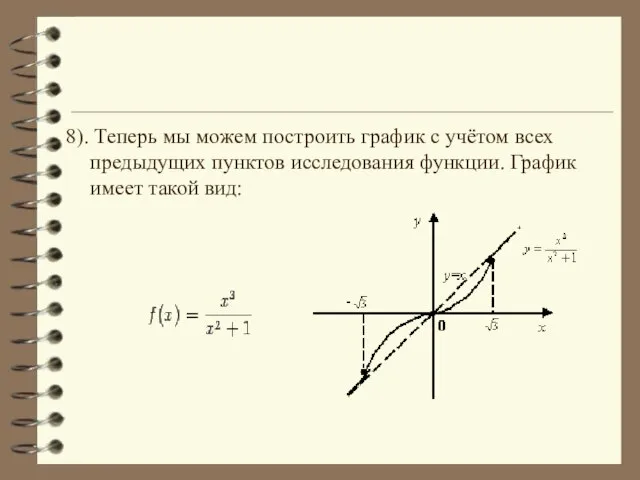
- 26. 8). Теперь мы можем построить график с учётом всех предыдущих пунктов исследования функции. График имеет такой
- 27. Исследуем функцию f(x) = (x2 – 2x)ex и построим её график. 1). Ясно, что D(f) =
- 28. 4) Будем искать наклонные асимптоты в виде y = kx + b. Коэффициент k найдём по
- 29. Теперь найдём значение b по формуле . Имеем: Таким образом, k=0 и b=0, так что при
- 30. Знак функции определяется множителем x2 – 2x, поскольку ex >0 при всех x. Значит, f(x)>0 при
- 31. Значение функции в этой точке равно В точке √2 убывание сменяется возрастанием, значит, точка √2 --
- 32. Становится очевидно, что область значений функции -- это 7) По эскизу графика видно, что где-то в
- 34. Скачать презентацию




























 Society and Social Interaction
Society and Social Interaction Скифы 11 класс
Скифы 11 класс Конфликтогены и техники профилактики конфликтов
Конфликтогены и техники профилактики конфликтов Дети Великой Отечественной войны
Дети Великой Отечественной войны Освоение углеводородных ресурсов полуострова Ямал
Освоение углеводородных ресурсов полуострова Ямал Использование инновационных технологий в обучении химии
Использование инновационных технологий в обучении химии Стихи и песни о Великой Отечественной войне
Стихи и песни о Великой Отечественной войне Критерии оценивания проектной деятельности и презентаций
Критерии оценивания проектной деятельности и презентаций Предмет и метод учебного курса Законодательная техника
Предмет и метод учебного курса Законодательная техника СЕМЕН ЗАХАРЫЧ МАРМЕЛАДОВ
СЕМЕН ЗАХАРЫЧ МАРМЕЛАДОВ Презентация на тему Индустриальная революции
Презентация на тему Индустриальная революции 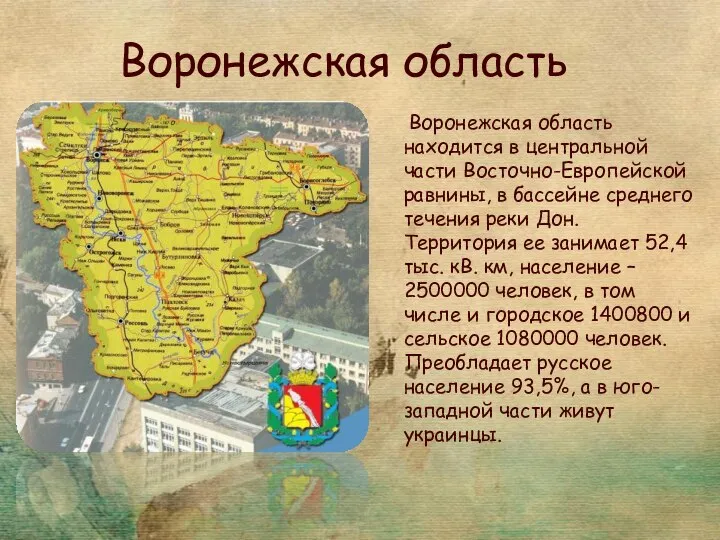 Воронежская область
Воронежская область ВИНО 1 часть
ВИНО 1 часть Отчет о реализации плана мероприятий Правительства Тверской области
Отчет о реализации плана мероприятий Правительства Тверской области Биология - совокупность наук о живом…
Биология - совокупность наук о живом… Бизнес-план проекта творческого развития детей SitPlay
Бизнес-план проекта творческого развития детей SitPlay Координационный совет по организации отдыха, оздоровления и занятости детей
Координационный совет по организации отдыха, оздоровления и занятости детей Презентация на тему Виды жилых помещений
Презентация на тему Виды жилых помещений  Present Simple
Present Simple  Коммерческое предложение по Генеральному спонсорству проекта «X Фактор» в эфире телеканала «Первый Канал «Евразия»
Коммерческое предложение по Генеральному спонсорству проекта «X Фактор» в эфире телеканала «Первый Канал «Евразия» История утюга. Параметры Braun TexStyle 7 TS 785 STP
История утюга. Параметры Braun TexStyle 7 TS 785 STP Стратегии
Стратегии С Прощёным воскресеньем, дорогие читатели!
С Прощёным воскресеньем, дорогие читатели! Time-менеджмент для управления своей жизнью
Time-менеджмент для управления своей жизнью Славный народ - собаки
Славный народ - собаки Использование национально-регионального компонента в обучении химии на элективных курсах
Использование национально-регионального компонента в обучении химии на элективных курсах Социальное государство. Задания для выполнения
Социальное государство. Задания для выполнения Лидия Алексеевна Чарская
Лидия Алексеевна Чарская