Содержание
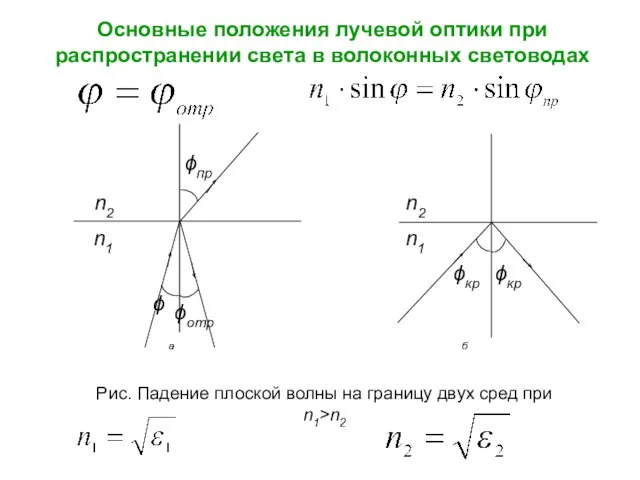
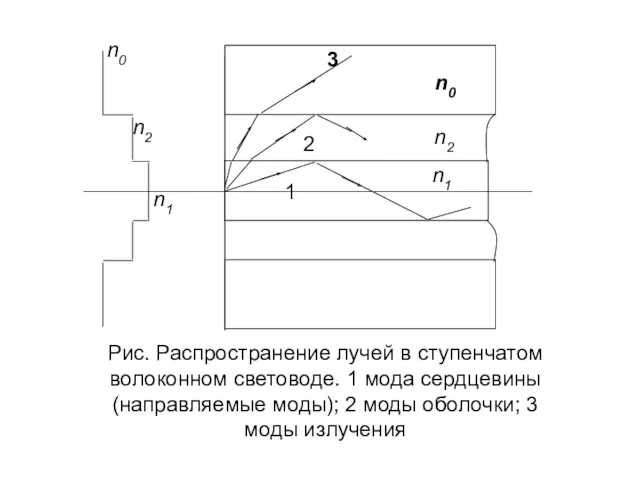
- 2. Основные положения лучевой оптики при распространении света в волоконных световодах
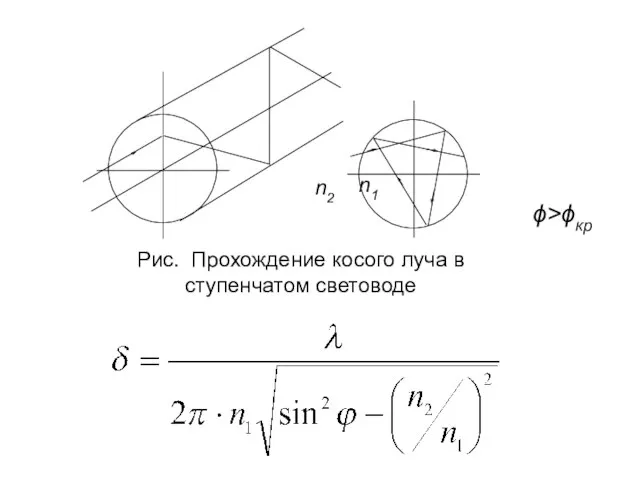
- 4. ϕ>ϕкр
- 7. или
- 11. Δn=10-2 – 10-3
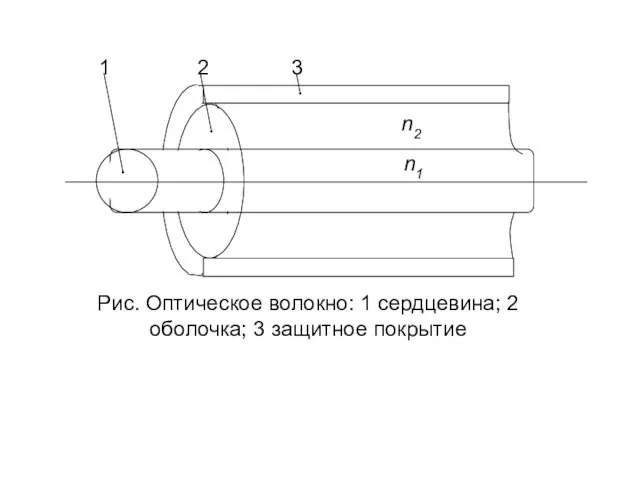
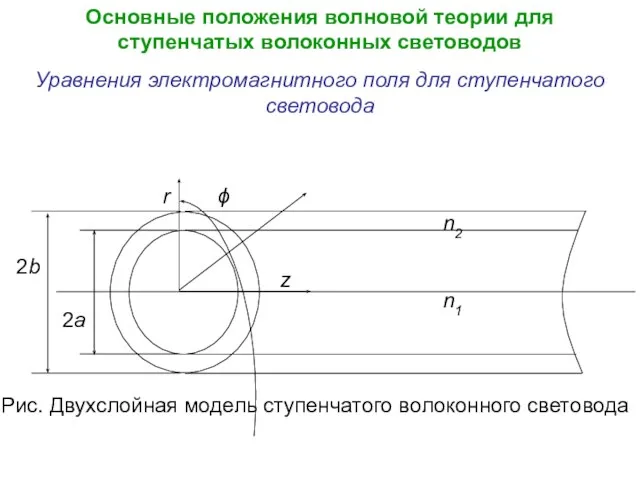
- 13. Основные положения волновой теории для ступенчатых волоконных световодов Уравнения электромагнитного поля для ступенчатого световода
- 15. Для монохроматических гармонических полей, для которых
- 16. Примем следующие условия 1. Считаем, что поле на внешней поверхности оптической оболочки пренебрежимо мало, т.е. можно
- 17. 2. Известно, что на поверхности раздала двух диэлектрических сред с различными значениями ε граничные условия для
- 18. 3. При анализе решений поставленной задачи следует иметь в виду, что функции, описывающие поведение поля в
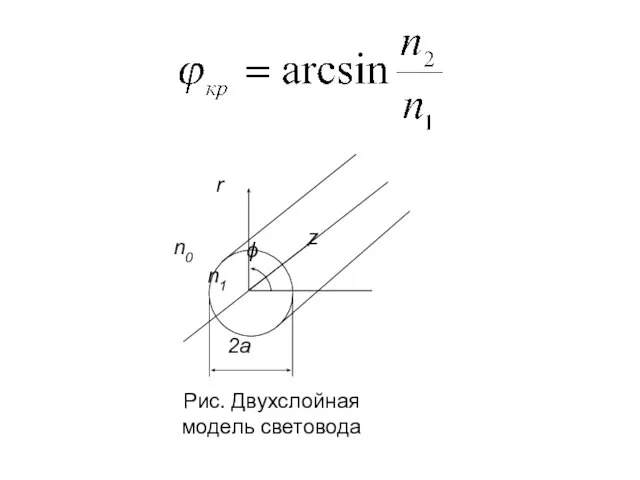
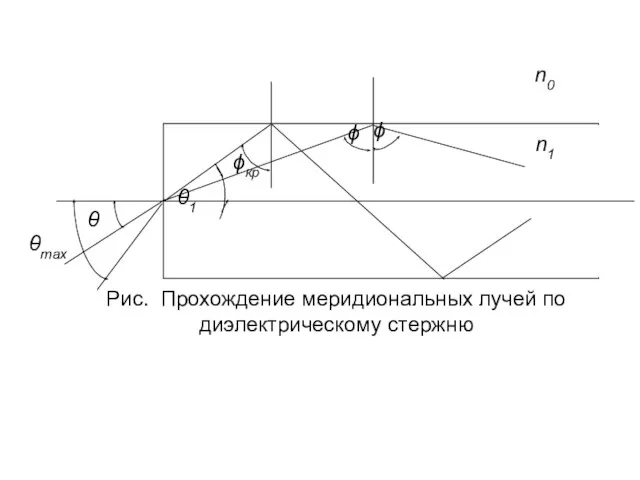
- 19. 4. Принимаем цилиндрическую систему координат r, ϕ, z, причем ось z совмещаем с осью световода. Распространяющиеся
- 20. Определение составляющих электромагнитного поля. Дисперсионное уравнение уравнение Максвелла в цилиндрической системе координат
- 21. g1 – поперечная составляющая волнового числа в сердцевине; β – коэффициент распространения в световоде; k1 –
- 24. для сердцевины Для оболочки
- 25. поперечная составляющая волнового числа в оболочке световода
- 27. для коэффициента распространения β, которое носит название дисперсионного уравнения
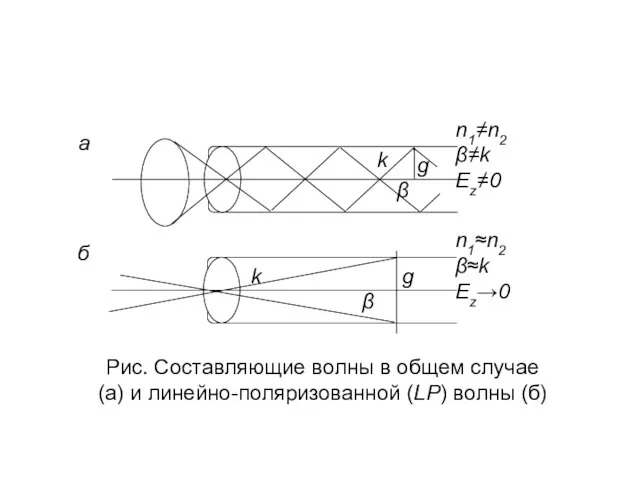
- 28. Характеристики распространения и типы направляемых волн Для симметричных волн
- 29. Для несимметричных дипольных волн
- 31. Характеристическое уравнение для LP мод имеет весьма простую форму Для одномодовой системы, которая работает на гибридной
- 32. Коэффициент распространения может быть рассчитан по формуле В предельных случаях при критической частоте (f0) и больших
- 33. определим критическую частоту световода:
- 34. критическая длина волны
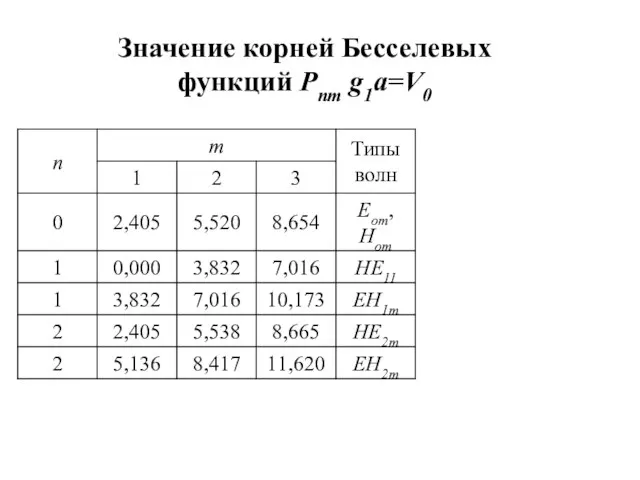
- 35. Значение корней Бесселевых функций Pnm g1a=V0
- 36. нормированная частота Значения нормированной частоты и тип соответствующей моды
- 37. При значении g1а=2,405 критическая частота использования одномодового волокна Число типов волн в световоде зависит от диаметра
- 38. Обычно и лежит в пределах Δ=0,003 – 0,01
- 39. Для градиентного световода, имеющего параболический профиль показателя преломления и=2 получается Для ступенчатого профиля показателя преломления показатель
- 40. число мод для ступенчатого волокна для градиентного
- 41. Фазовая и групповая скорости. Волновое сопротивление
- 43. Групповая скорость распространения по световоду определяется выражением
- 44. Волновое сопротивление световода предельное значения волнового сопротивления сердцевины оболочки
- 46. Скачать презентацию
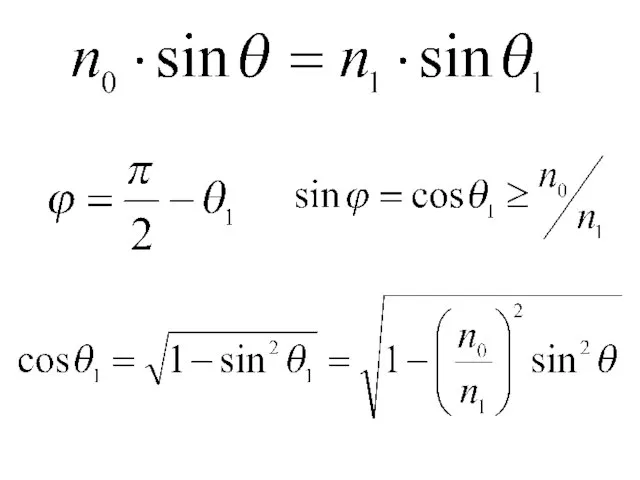
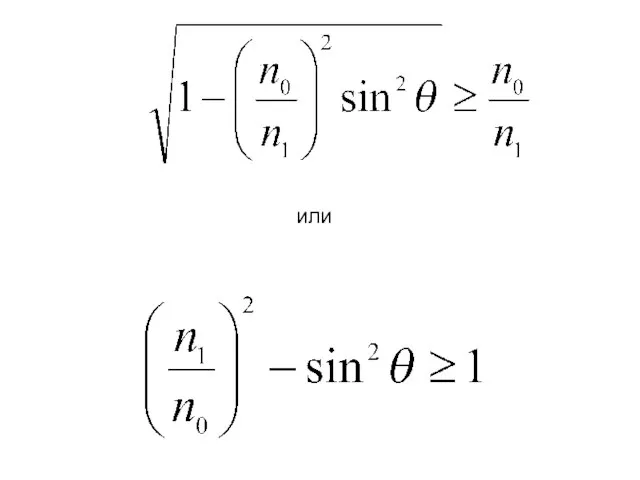
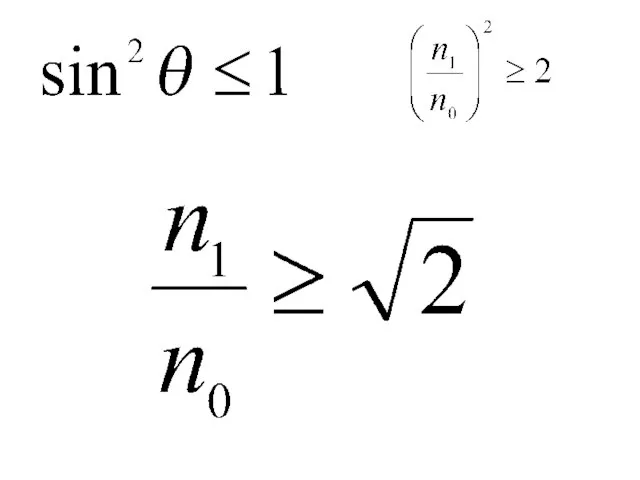
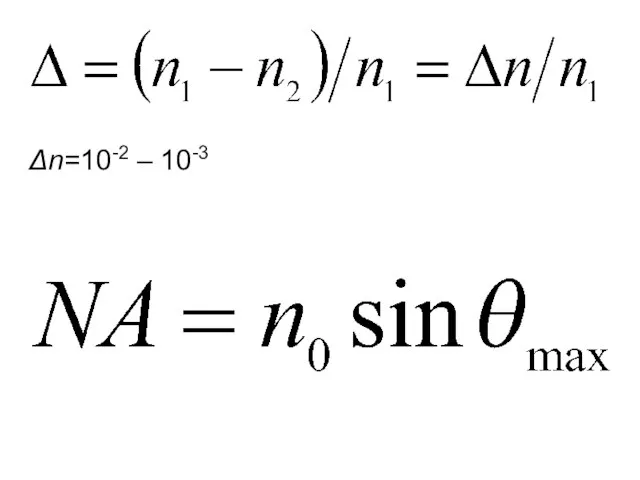
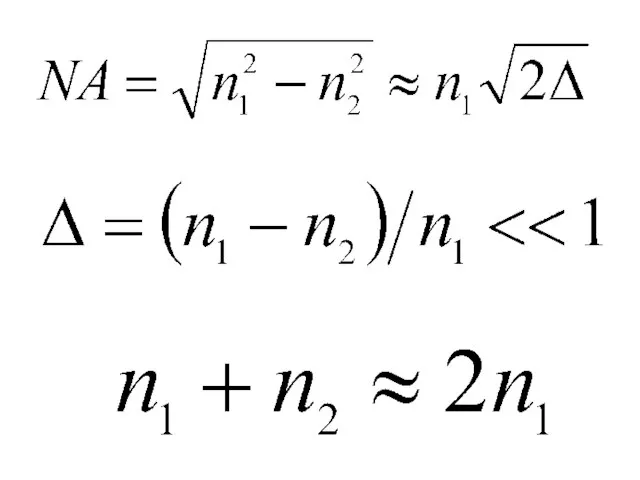
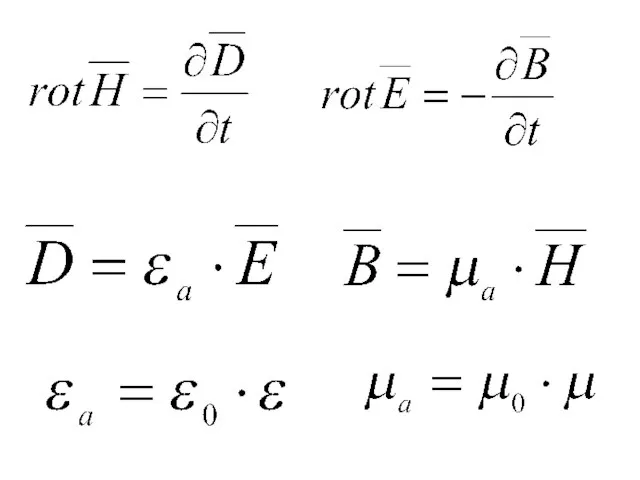
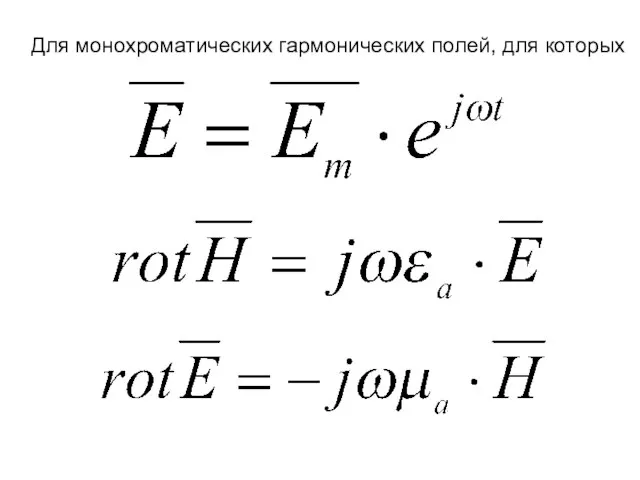






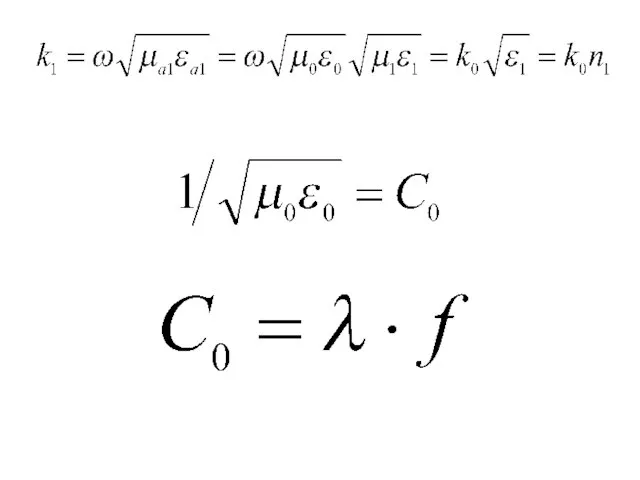
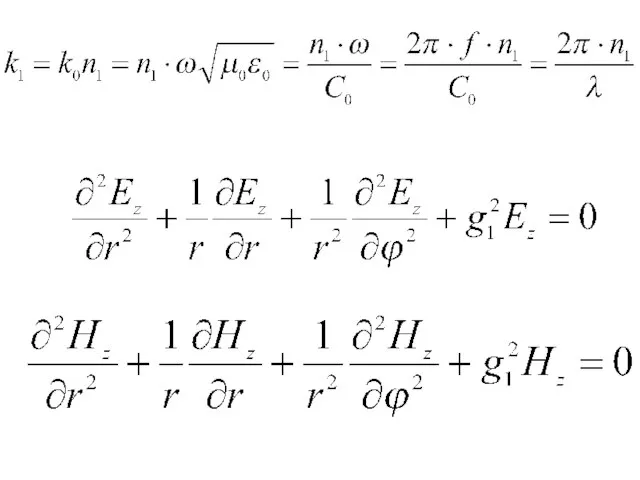
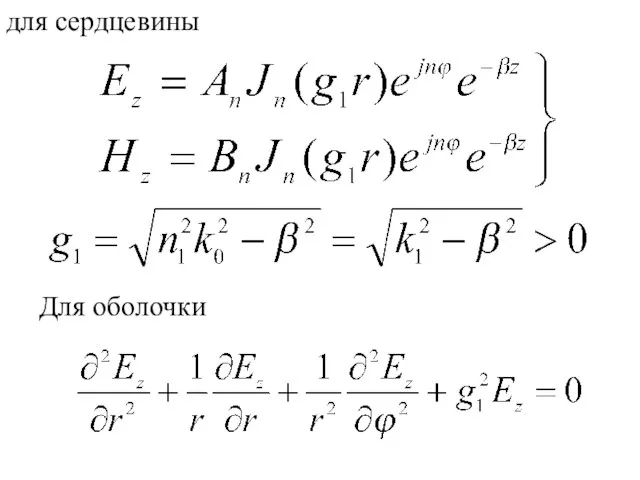

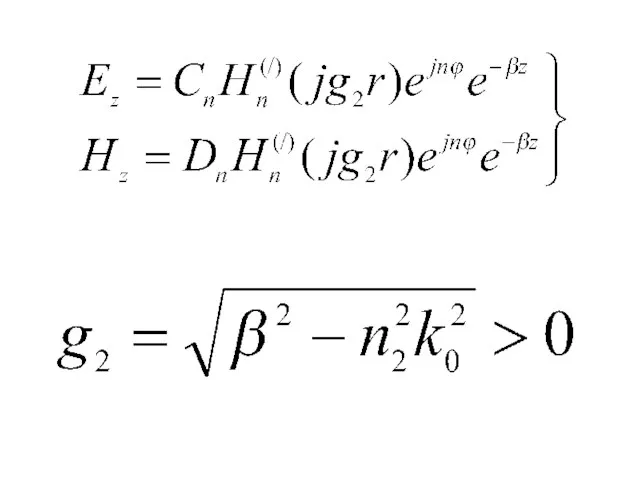





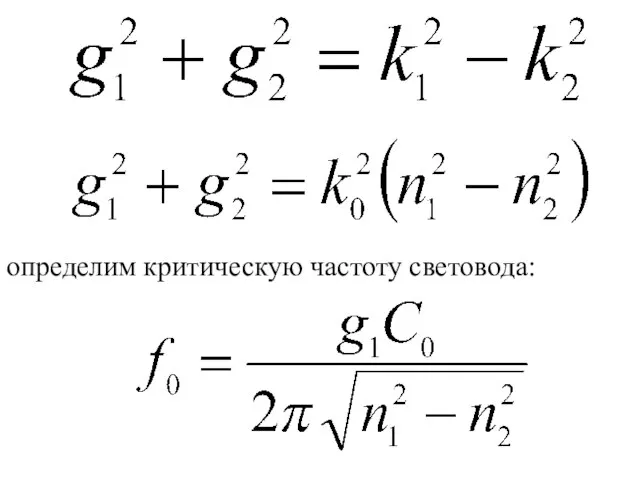
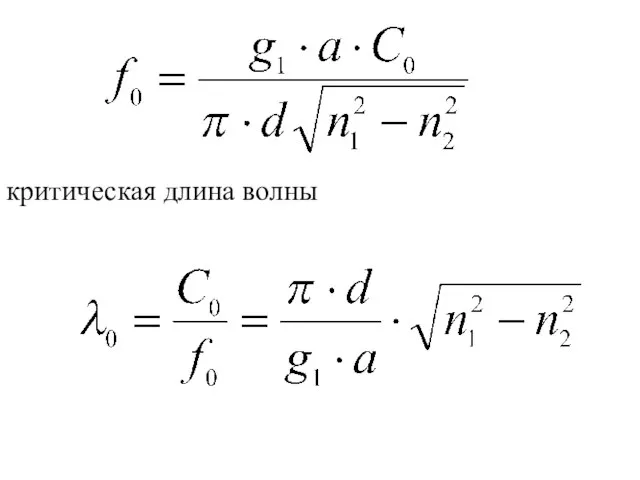






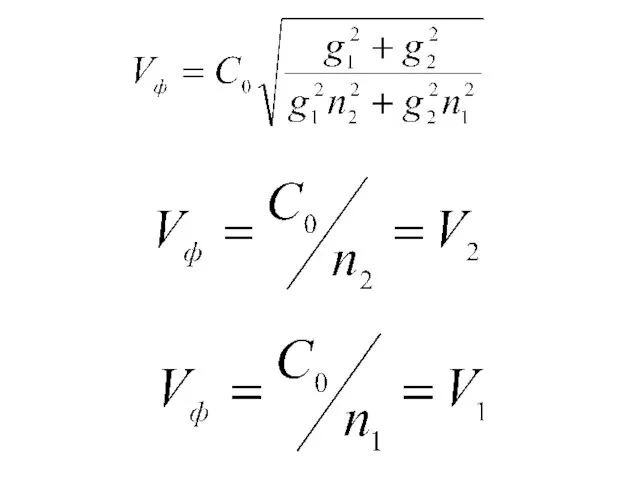
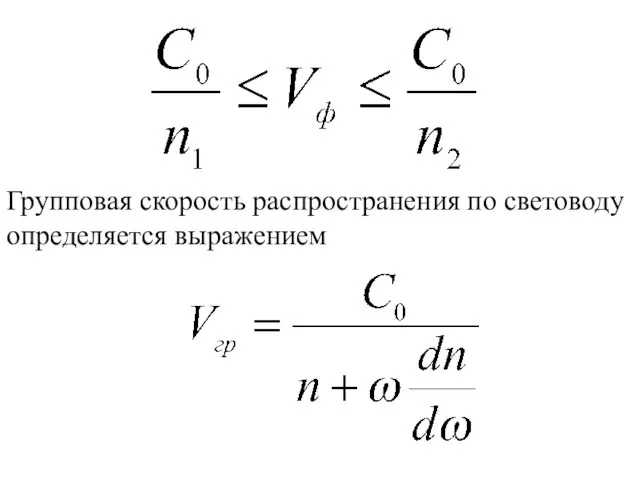

 Африка
Африка Тууль Максим Юрьевич «Клуб Участников Проектного Процесса», Директор АКБ «Надежный банк», Президент тел: (495) 7675=02=23; E-mail: TMY@proje
Тууль Максим Юрьевич «Клуб Участников Проектного Процесса», Директор АКБ «Надежный банк», Президент тел: (495) 7675=02=23; E-mail: TMY@proje Илларион Михайлович Прянишников (1840-1894)
Илларион Михайлович Прянишников (1840-1894) ТЕРРИТОРИЯ ЛЮБВИ
ТЕРРИТОРИЯ ЛЮБВИ Презентация на тему И.С. Тургенева «Муму»
Презентация на тему И.С. Тургенева «Муму»  Презентація 10 клас Урок 31
Презентація 10 клас Урок 31 Ассирийская держава
Ассирийская держава Презентация 2
Презентация 2 Сертификация систем качества
Сертификация систем качества История развития зоологии
История развития зоологии Реализуемое имущество АО РоссельхозБанк: транспортные средства, с/х техника и оборудование
Реализуемое имущество АО РоссельхозБанк: транспортные средства, с/х техника и оборудование Обработка нижних срезов рукавов
Обработка нижних срезов рукавов Давайте знакомиться!
Давайте знакомиться! Мой первый бизнес-план
Мой первый бизнес-план Украшения своими руками
Украшения своими руками Стратегическое планирование и его этапы. Планирование маркетинга. Контроль. Типы маркетингового контроля
Стратегическое планирование и его этапы. Планирование маркетинга. Контроль. Типы маркетингового контроля Требования к информации, формируемой в бухгалтерском учете
Требования к информации, формируемой в бухгалтерском учете Центр«Интеллектуальные электронные энергосберегающие системы»(ЦИЭС)
Центр«Интеллектуальные электронные энергосберегающие системы»(ЦИЭС) Защитные очки
Защитные очки Карельский научный центр Российской академии наук. Молодые учёные
Карельский научный центр Российской академии наук. Молодые учёные История Т-34
История Т-34 По страницам русского языка
По страницам русского языка Ксюша
Ксюша Урок 20.1. Перевод дела в архив (на примере гражданского дела)
Урок 20.1. Перевод дела в архив (на примере гражданского дела) Презентация на тему Имена существительные нарицательные и собственные
Презентация на тему Имена существительные нарицательные и собственные Аудитория украинского интернета: статистика и тенденции
Аудитория украинского интернета: статистика и тенденции Любить но кого же?
Любить но кого же? Право, семья, ребенокКравченко, 9 класс
Право, семья, ребенокКравченко, 9 класс