Содержание
- 2. Задача 1
- 3. 1) 0,07; 0,105; 0,0157 2) 0,0157; 0,105; 0,07 3) 0,105; 0,07; 0,0157 4) 0,0157; 0,07; 0,105
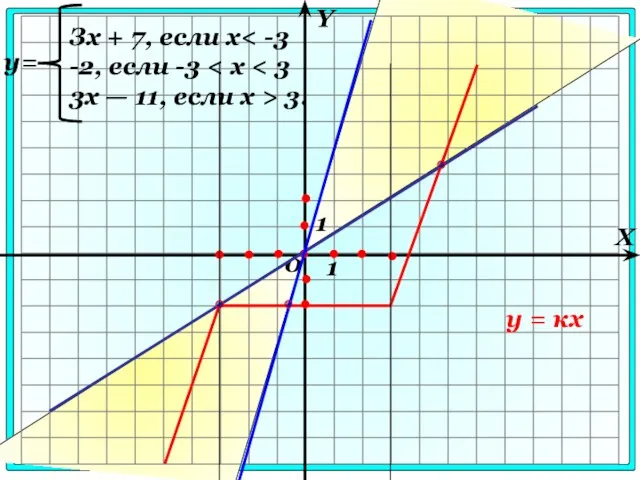
- 4. 1 2 3 4 [0,1; 0,2] [0,2; 0,3] [0,3; 0,4] [0,4; 0,5] 1 2 3 4
- 5. Задача 2
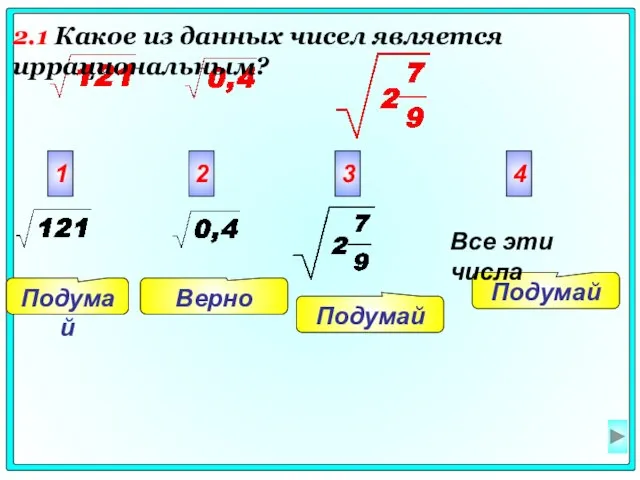
- 6. Подумай Подумай Верно Подумай 1 2 3 4 Все эти числа 2.1 Какое из данных чисел
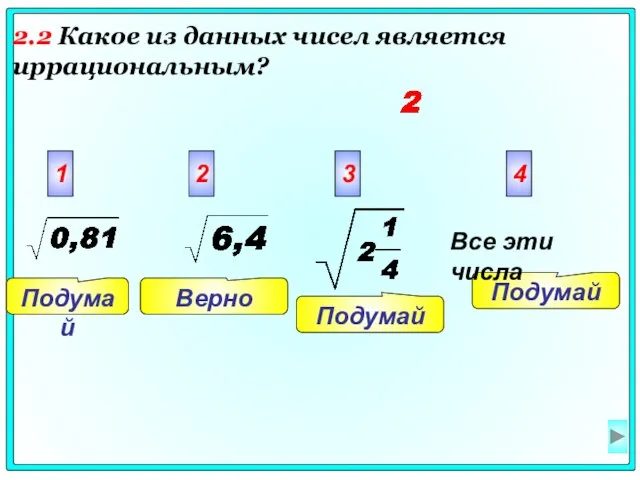
- 7. Подумай Подумай Верно Подумай 1 2 3 4 Все эти числа 2.2 Какое из данных чисел
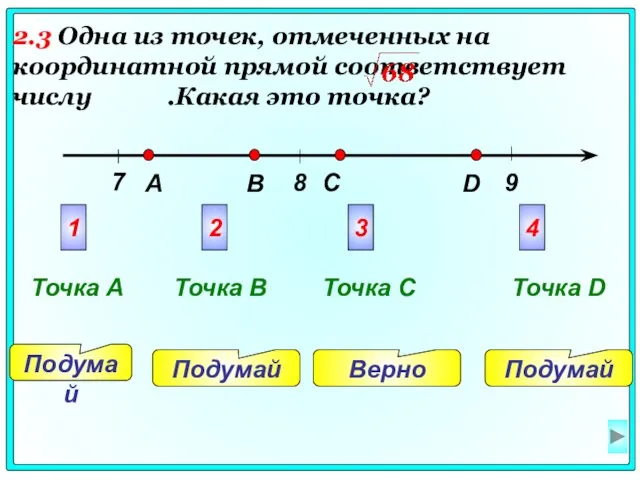
- 8. 8 7 9 A B C D Подумай Верно Подумай Подумай 1 2 3 4 Точка
- 9. 2.4. В деревне Дубровка живет 72 человека, а ее площадь 9 км2. Каково среднее количество жителей
- 10. 2.9. Население Австрии составляет 8,26 • 10 6 человек. Чему равно население Австрии в миллионах человек?
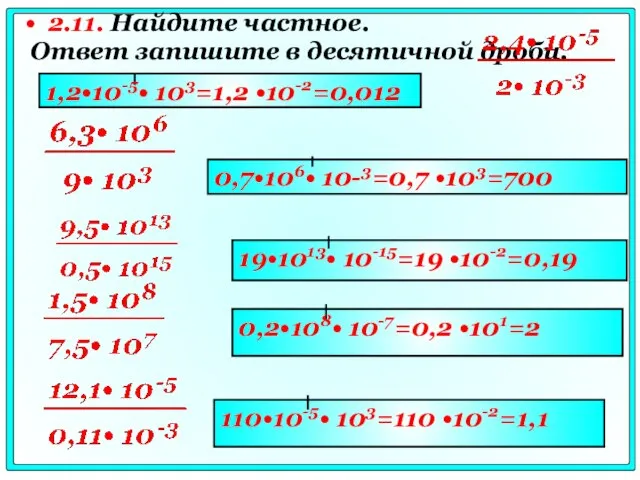
- 11. 2.11. Найдите частное. Ответ запишите в десятичной дроби. 1,2•10-5• 103=1,2 •10-2=0,012 0,7•106• 10-3=0,7 •103=700 19•1013• 10-15=19
- 12. Зачетные задания Задача 2
- 13. 1. Завод за год выпустил4,7 • 10 8 одинаковых бутылок с водой, при этом воды в
- 14. 2.Население Дании составляет 5,4•10 6 человек, а ее территория равна 4,3• 10 4 км2. Какой из
- 15. Задача 3
- 16. 3.1. Укажите число, соответствующее 10%. 1) 0,1 2) 0,01 3) 1 4) 10 3.2. Укажите число
- 17. 3,6. Из объявления фирмы, проводящей обучающие семинары: «Стоимость участия в семинаре — 3000 р. с человека.
- 18. 3,7. Из объявления фирмы, проводящей обучающие семинары:«Стоимость участия в семинаре — 2000 р. с человека. Группам
- 19. 3.8. Цена товара 200 р. В понедельник эту цену уменьшили на 10%. По какой цене продавался
- 20. Зачетные задания Задача 3
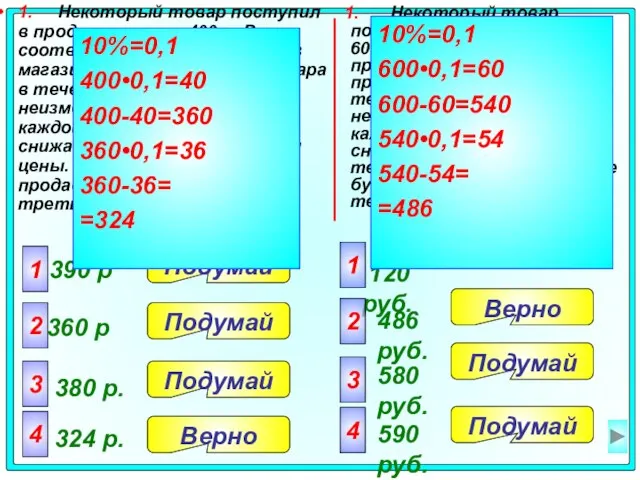
- 21. 1. Некоторый товар поступил в продажу по цене 600 р. В соответствии с принятыми в магазине
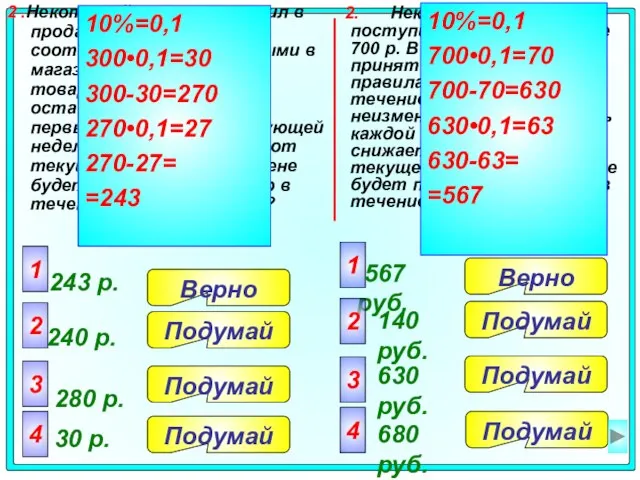
- 22. 2. Некоторый товар поступил в продажу по цене 700 р. В соответствии с принятыми в магазине
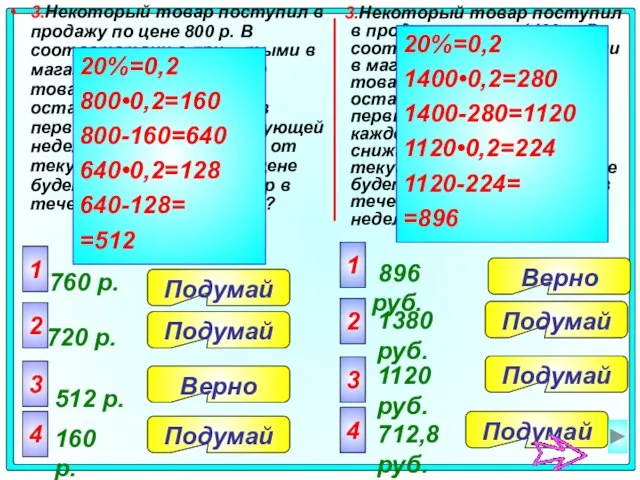
- 23. 3.Некоторый товар поступил в продажу по цене 1400 р. В соответствии с принятыми в магазине правилами,
- 24. Задача 4
- 25. 4. Зная длину своего шага, человек может подсчитать пройденное им расстояние s по формуле: s =
- 26. 4.1. Выразите в километрах а)600000 см = км; г) 3510000 см = км; б)36000 м =
- 27. Зачетные задания Задача 4
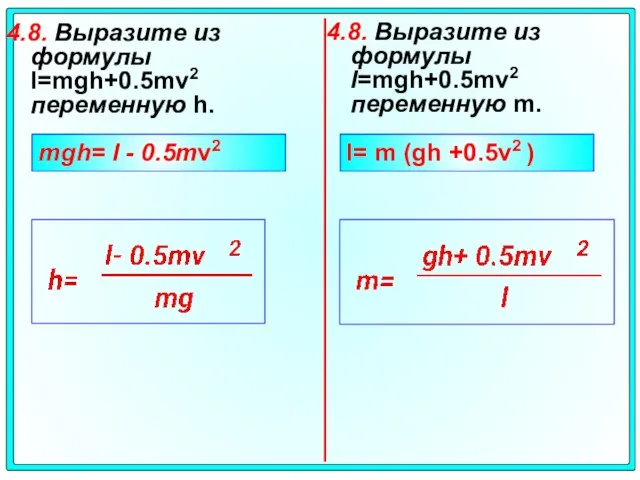
- 28. 4.8. Выразите из формулы l=mgh+0.5mv2 переменную h. 4.8. Выразите из формулы l=mgh+0.5mv2 переменную m. 4.9.Зная скорость
- 29. 4.10.Зная скорость и время движения, человек может подсчитать пройденное им расстояние s по формуле: s =
- 30. 4.8. Выразите из формулы l=mgh+0.5mv2 переменную h. 4.8. Выразите из формулы l=mgh+0.5mv2 переменную m. mgh= l
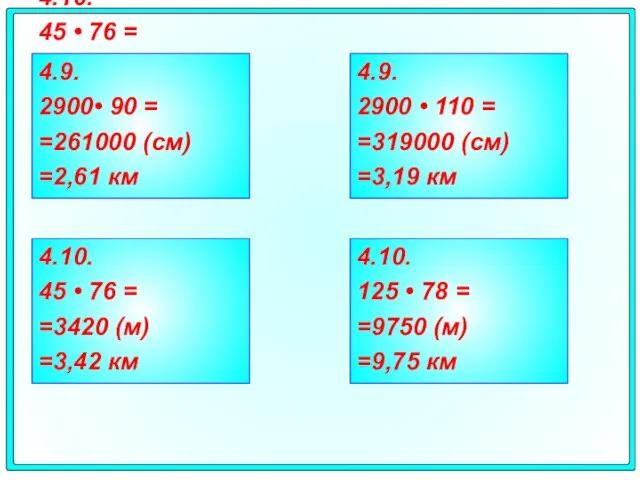
- 31. 4.10. 45 • 76 = =3420 (м) =3,42 км 4.10. 45 • 76 = =3420 (м)
- 32. Задача 5
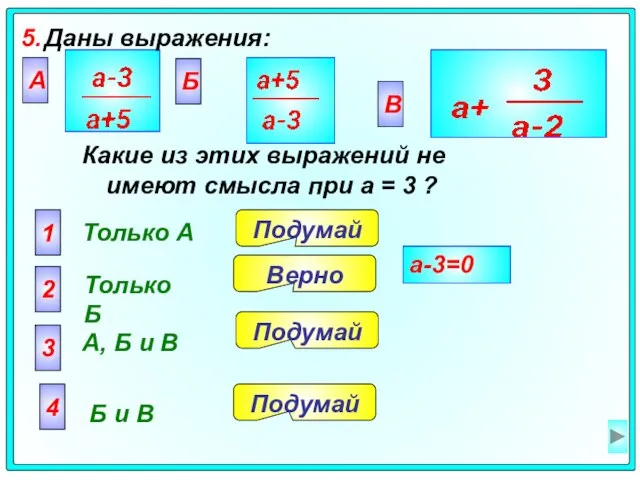
- 33. 5. Даны выражения: А Только A 2 Только Б 3 А, Б и В 4 Б
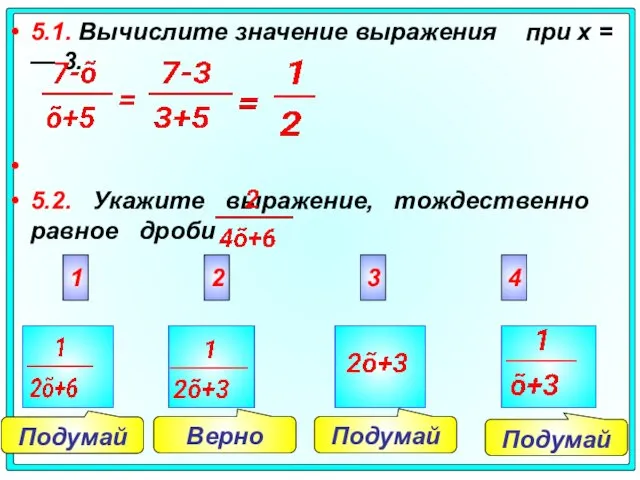
- 34. Подумай Подумай Подумай Верно 5.1. Вычислите значение выражения при х = — 3. 5.2. Укажите выражение,
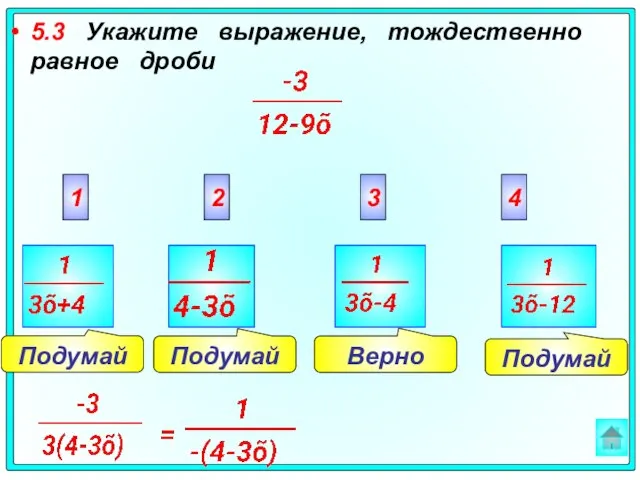
- 35. Подумай Верно Подумай Подумай 5.3 Укажите выражение, тождественно равное дроби 2 3 4 1
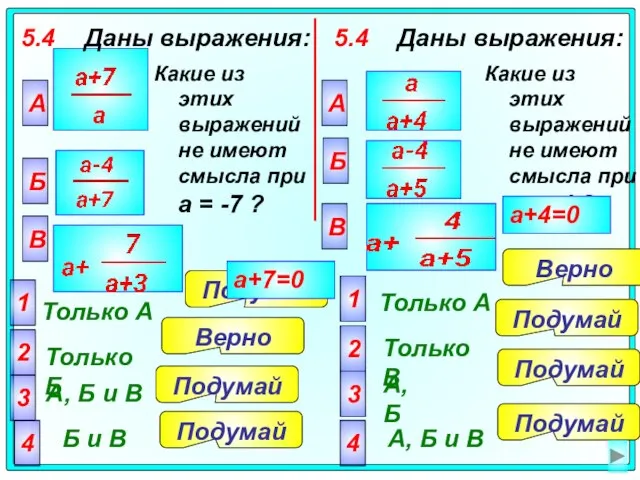
- 36. 5.4 Даны выражения: А Только A 2 Только Б 3 А, Б и В 4 Б
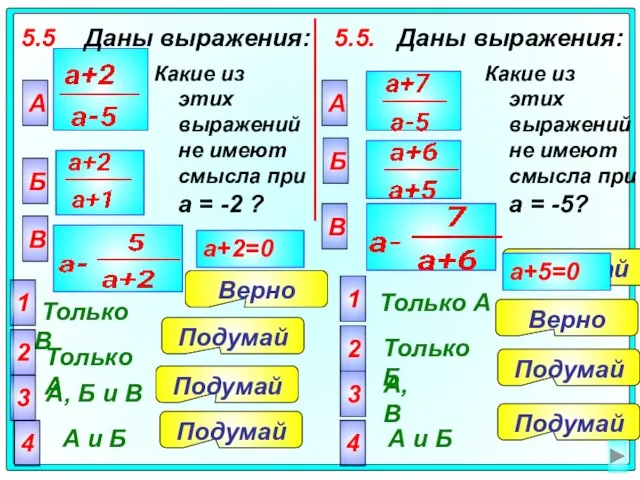
- 37. 5.5 Даны выражения: А Только В 2 Только А 3 А, Б и В 4 А
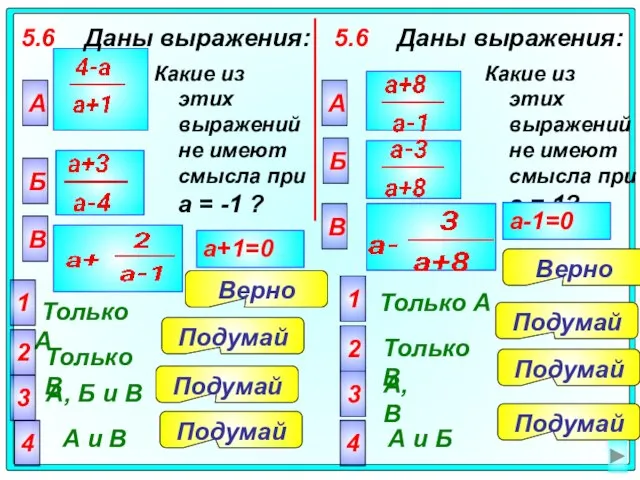
- 38. 5.6 Даны выражения: А Только А 2 Только В 3 А, Б и В 4 А
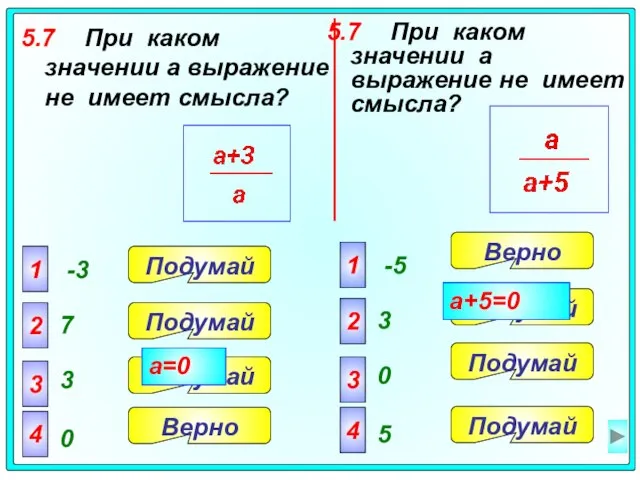
- 39. 5.7 При каком значении a выражение не имеет смысла? 5.7 При каком значении a выражение не
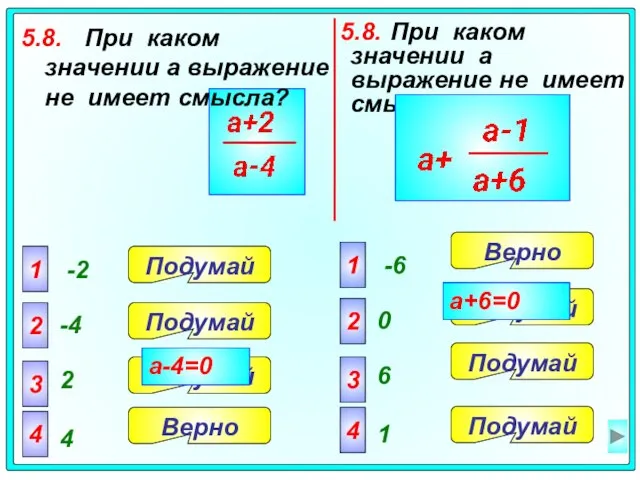
- 40. 5.8. При каком значении a выражение не имеет смысла? 5.8. При каком значении a выражение не
- 41. Задача 6
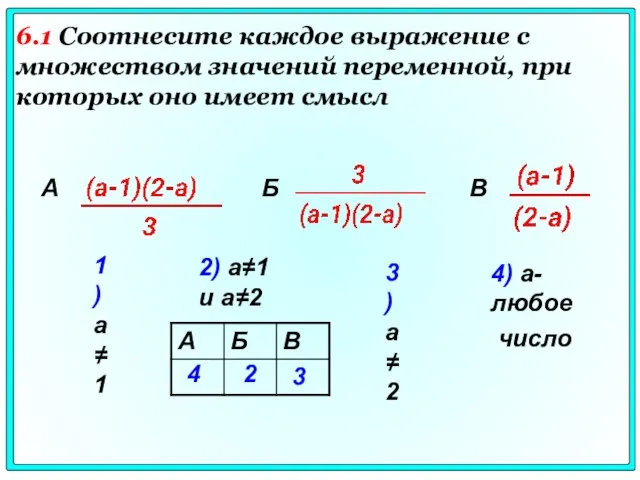
- 42. 1) а≠1 2) а≠1 и а≠2 3) а≠2 4) а- любое число 4 2 3 Б
- 43. 1) (a + b)2 = a2 + b2 2) (a + b)(b - a) = b2-
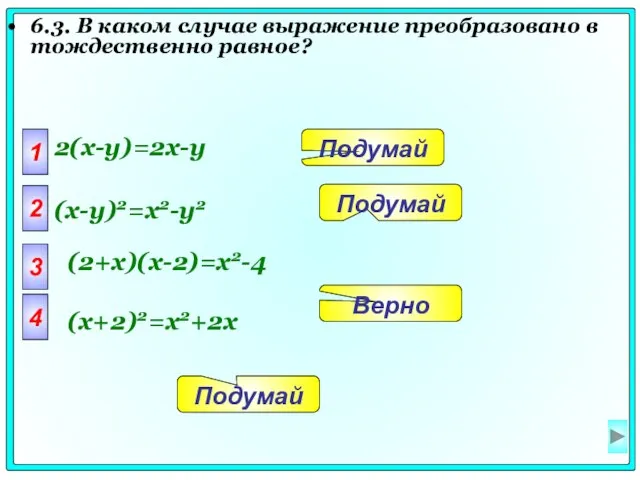
- 44. 6.3. В каком случае выражение преобразовано в тождественно равное? 1 2(x-y)=2x-y 2 3 4 Подумай Подумай
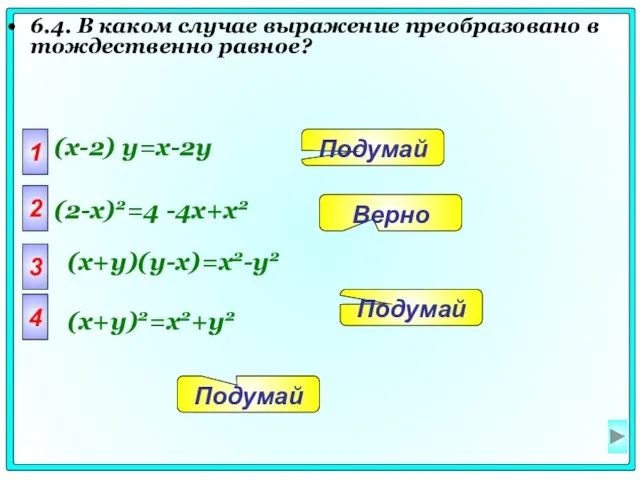
- 45. 6.4. В каком случае выражение преобразовано в тождественно равное? 1 (x-2) y=x-2y 2 3 4 Подумай
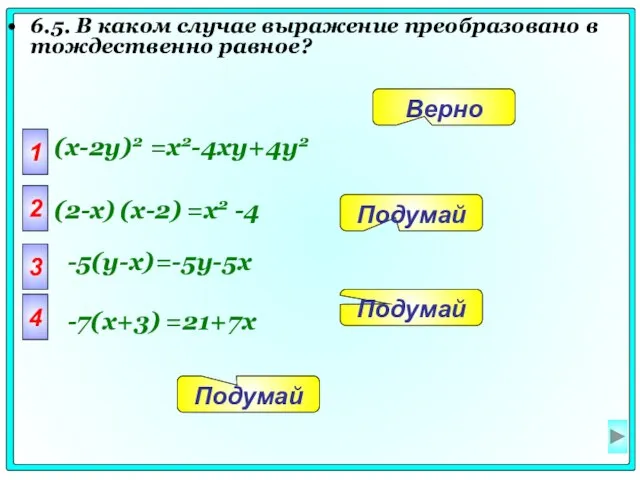
- 46. 6.5. В каком случае выражение преобразовано в тождественно равное? 1 (x-2y)2 =x2-4xy+4y2 2 3 4 Подумай
- 47. Задача 7
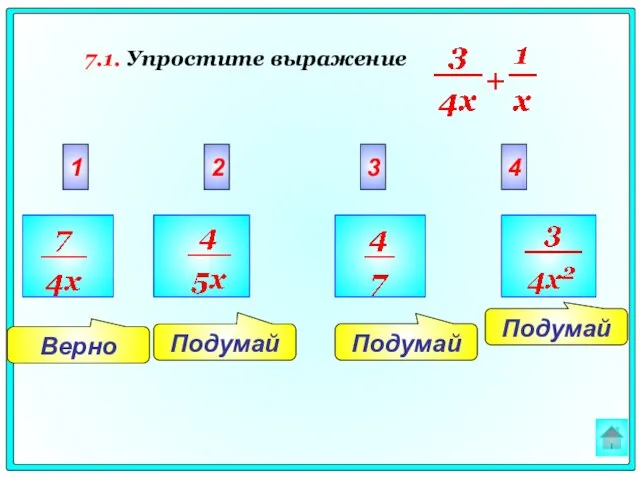
- 48. Подумай Верно Подумай Подумай 2 3 4 1 7.1. Упростите выражение
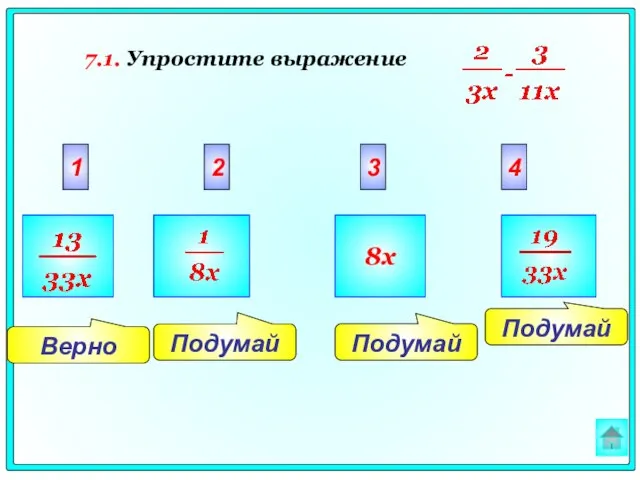
- 49. Подумай Верно Подумай Подумай 2 3 4 1 8x 7.1. Упростите выражение
- 50. Задача 8
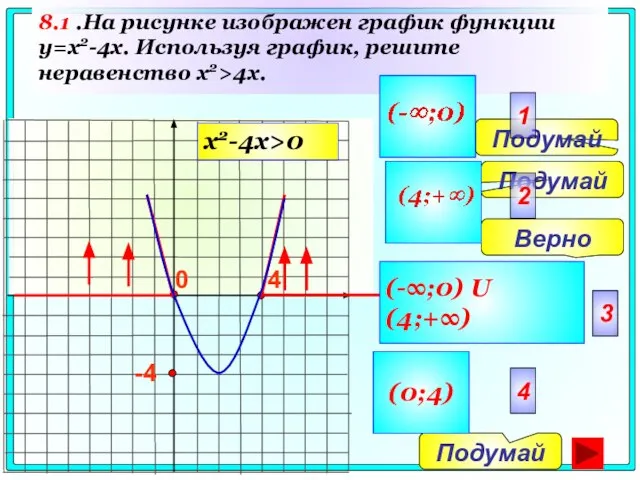
- 51. 8.1 .На рисунке изображен график функции y=x2-4x. Используя график, решите неравенство x2>4x. 4 0 -4 Подумай
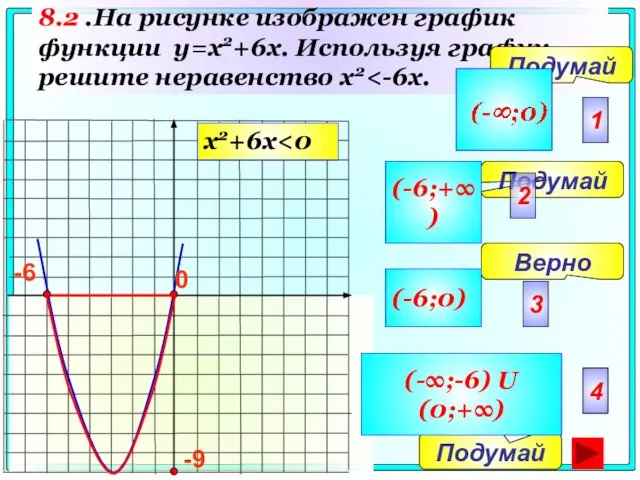
- 52. 8.2 .На рисунке изображен график функции y=x2+6x. Используя график, решите неравенство x2 0 Подумай Подумай Верно
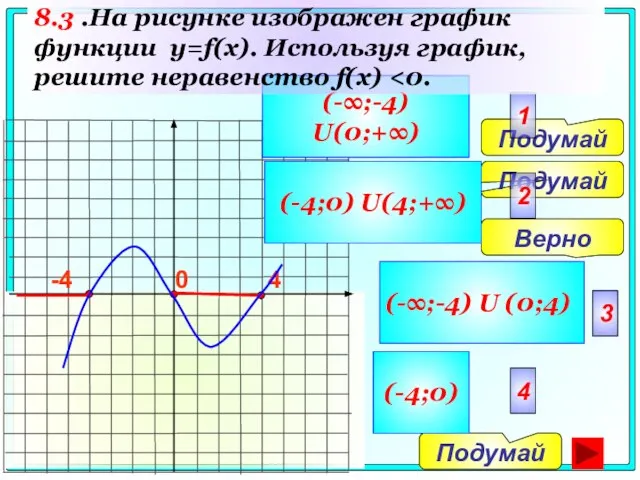
- 53. 4 0 Подумай Подумай Верно Подумай 2 3 4 1 (-∞;-4) U(0;+∞) (-4;0) U(4;+∞) (-∞;-4) U
- 54. Задача 9
- 55. Решите уравнение 9.1. 2x2-x-6=0 9.2 4x - 2 = 7 — 6(3 - x). 9.3. -3(2-x)=
- 56. 9.5 Решите уравнение - = 2 1 2 3 4 Верно Подумай Подумай Подумай -9 -6
- 57. 9.6 Решите уравнение = 0 1 2 3 4 Подумай Подумай Верно Подумай 2;-3 2 3
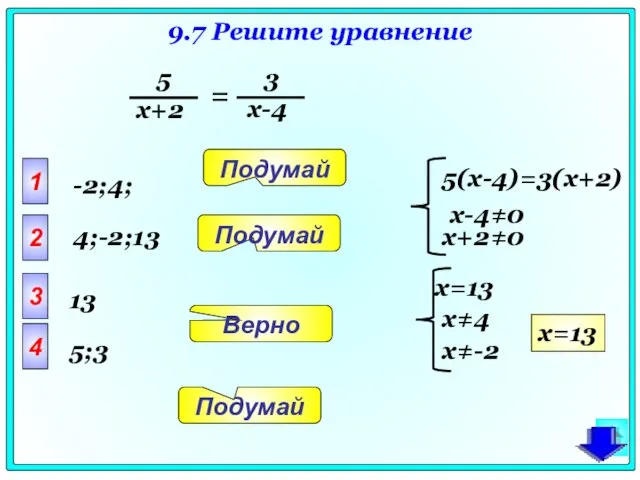
- 58. 9.7 Решите уравнение = 1 2 3 4 Подумай Подумай Верно Подумай 13 -2;4; 4;-2;13 5;3
- 59. Задача 10
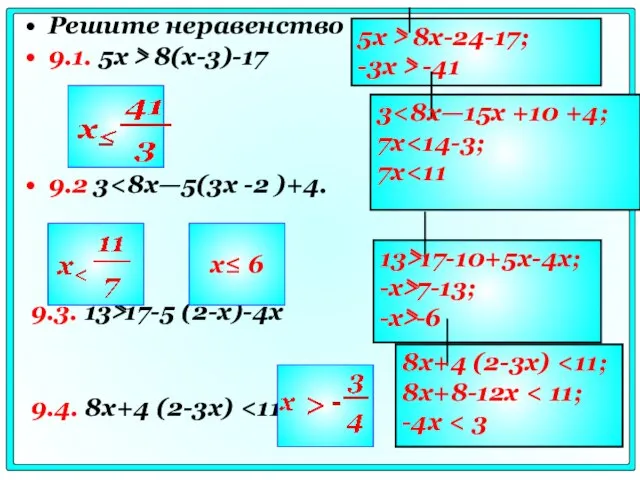
- 60. Решите неравенство 9.1. 5x ⋝ 8(x-3)-17 9.2 3 9.3. 13⋝17-5 (2-x)-4x 9.4. 8x+4 (2-3x) 5x ⋝
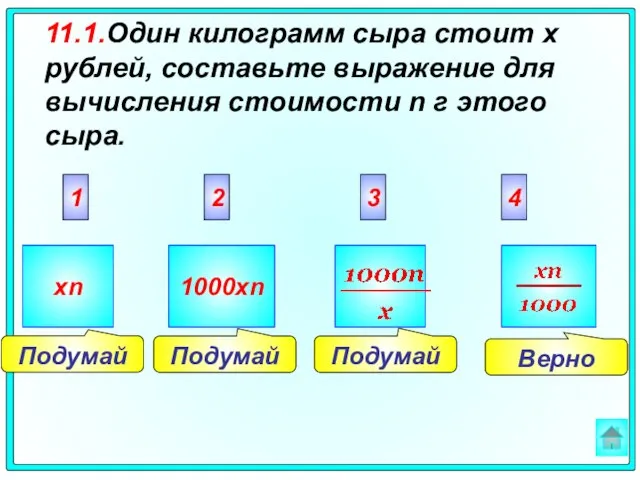
- 61. Решите неравенство 1 2 3 4 Подумай Подумай Подумай Верно x>-10 x 6-3x 3(1-x)-(2-x) x>-3 x
- 62. Задача 11
- 63. Верно Подумай Подумай Подумай 2 3 4 1 xn 1000xn 11.1.Один килограмм сыра стоит х рублей,
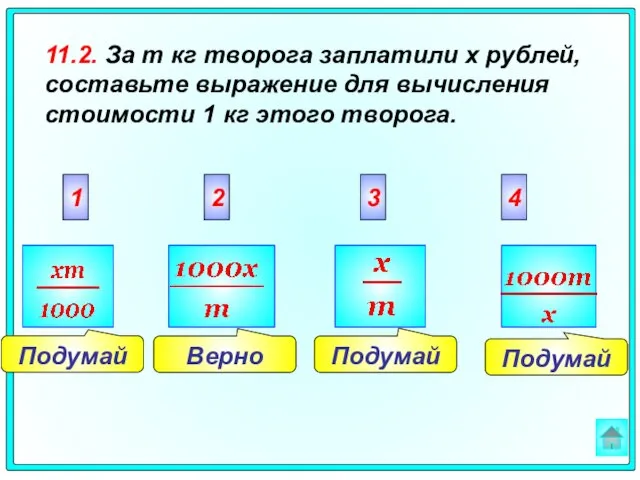
- 64. Подумай Подумай Подумай Верно 2 3 4 1 11.2. За m кг творога заплатили х рублей,
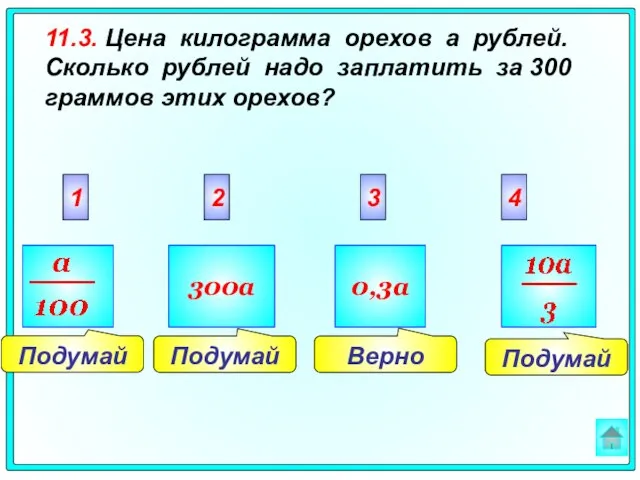
- 65. Подумай Верно Подумай Подумай 2 3 4 1 300a 0,3a 11.3. Цена килограмма орехов a рублей.
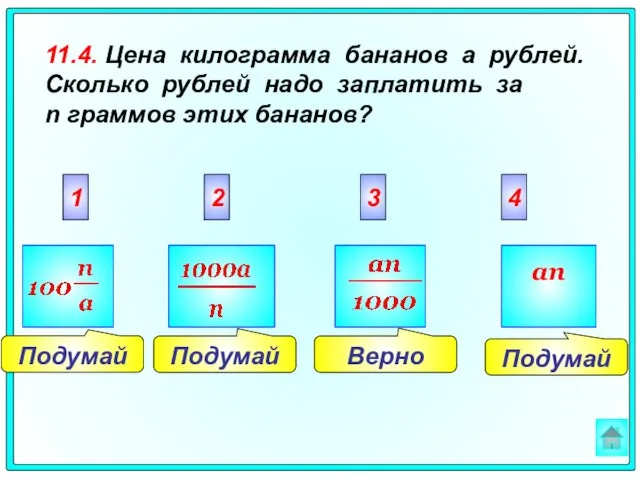
- 66. Подумай Верно Подумай Подумай 2 3 4 1 an 11.4. Цена килограмма бананов a рублей. Сколько
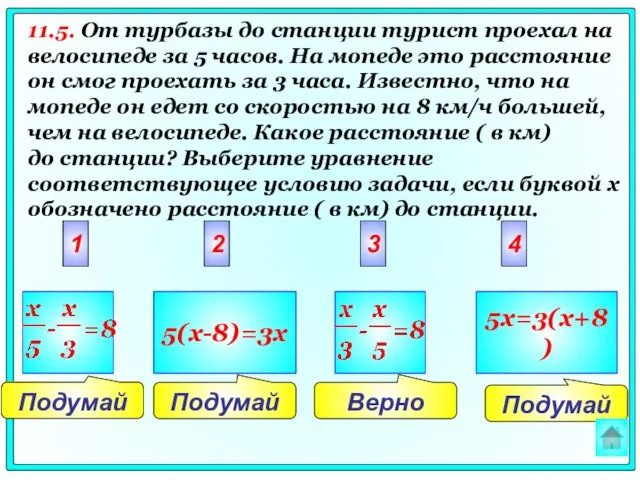
- 67. Подумай Верно Подумай Подумай 2 3 4 1 5(x-8)=3x 5x=3(x+8) 11.5. От турбазы до станции турист
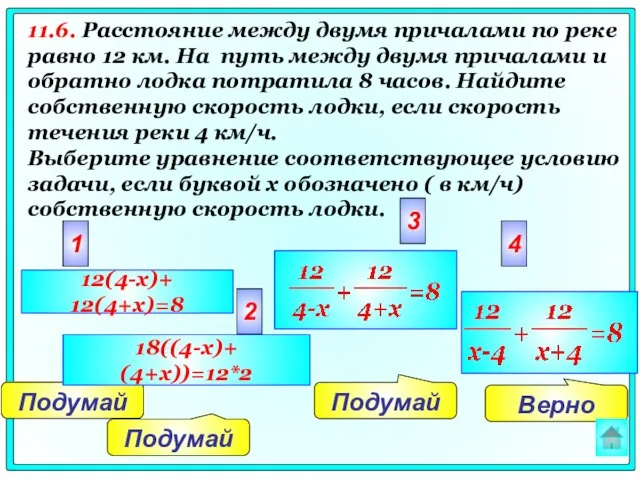
- 68. Верно Подумай Подумай Подумай 2 3 4 1 12(4-x)+ 12(4+x)=8 18((4-x)+ (4+x))=12*2 11.6. Расстояние между двумя
- 69. Задача 12
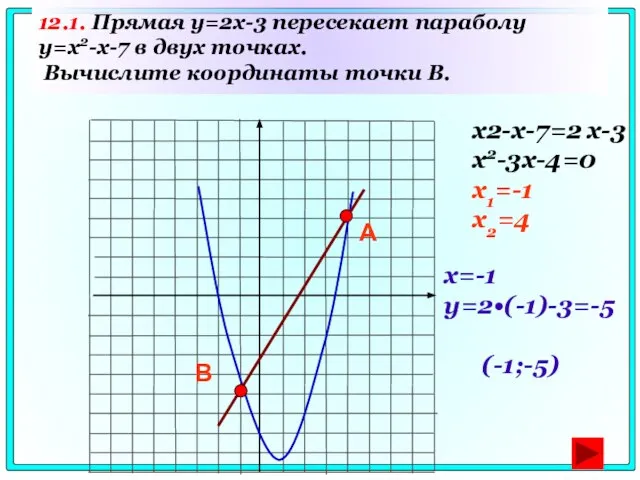
- 70. 12.1. Прямая y=2x-3 пересекает параболу y=x2-x-7 в двух точках. Вычислите координаты точки B. А В x2-x-7=2
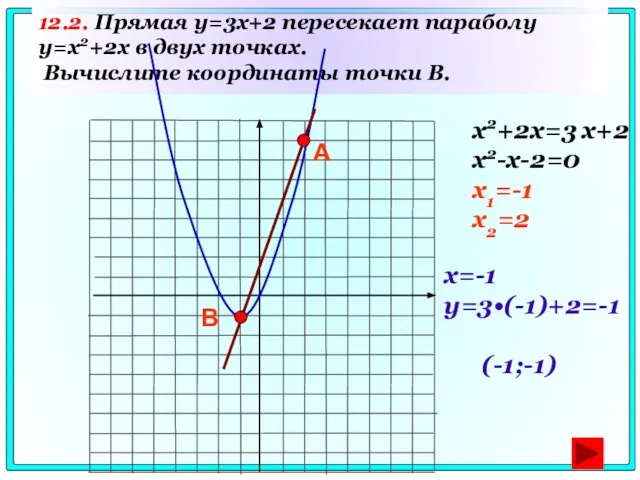
- 71. 12.2. Прямая y=3x+2 пересекает параболу y=x2+2x в двух точках. Вычислите координаты точки B. А В x2+2x=3
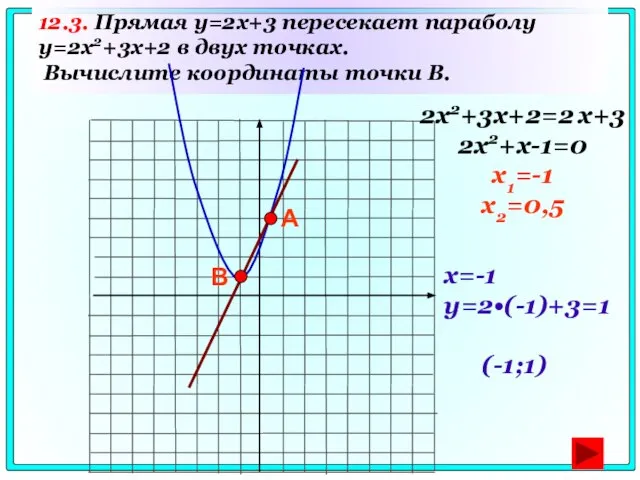
- 72. 12.3. Прямая y=2x+3 пересекает параболу y=2x2+3x+2 в двух точках. Вычислите координаты точки B. А В 2x2+3x+2=2
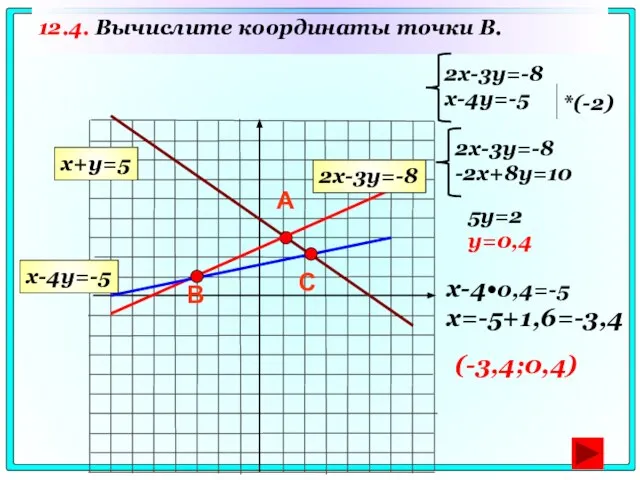
- 73. 12.4. Вычислите координаты точки B. А В 2x-3y=-8 x-4y=-5 x-4•0,4=-5 x=-5+1,6=-3,4 (-3,4;0,4) С 2x-3y=-8 x+y=5 x-4y=-5
- 74. Задача 13
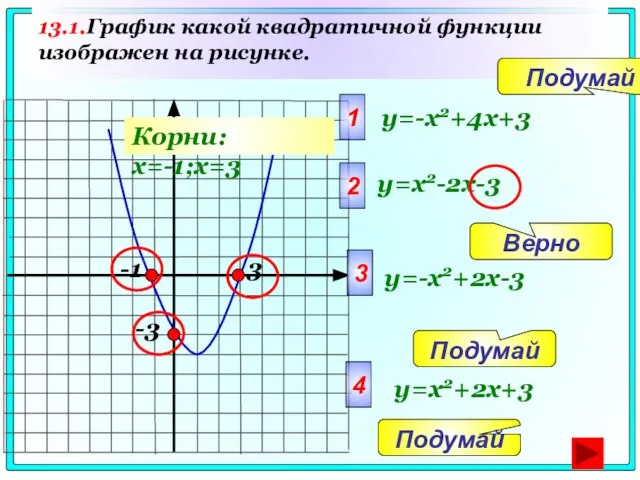
- 75. 13.1.График какой квадратичной функции изображен на рисунке. -3 1 y=-x2+4x+3 2 3 4 Подумай Подумай Верно
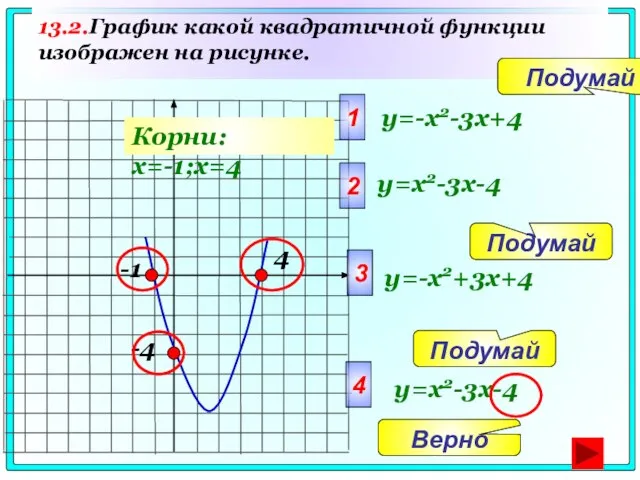
- 76. 13.2.График какой квадратичной функции изображен на рисунке. -4 1 y=-x2-3x+4 2 3 4 Верно Подумай Подумай
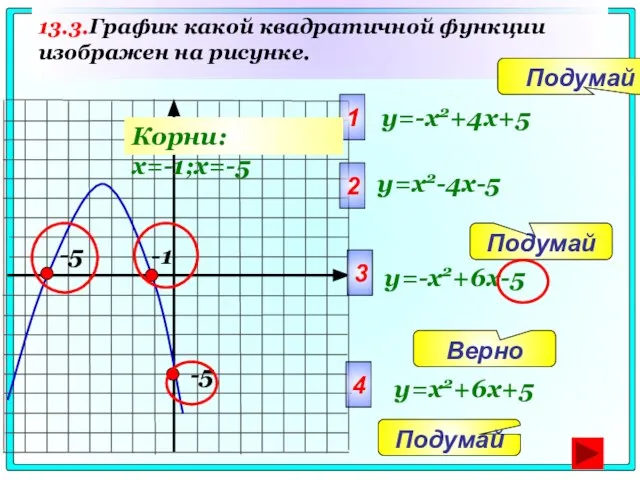
- 77. 13.3.График какой квадратичной функции изображен на рисунке. -5 1 y=-x2+4x+5 2 3 4 Подумай Подумай Подумай
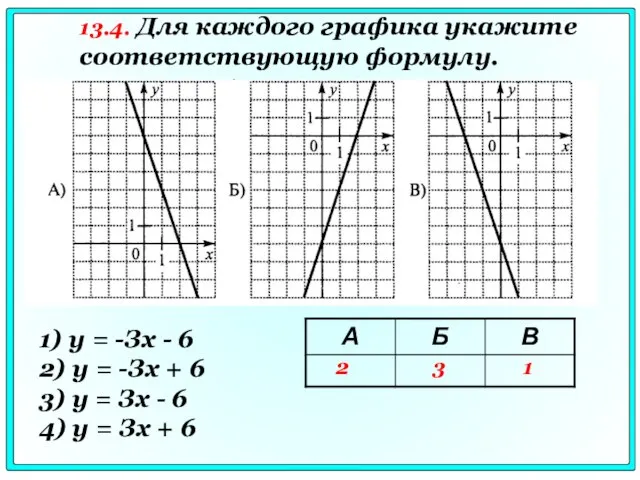
- 78. 1) у = -Зх - 6 2) у = -Зх + 6 3) у = Зх
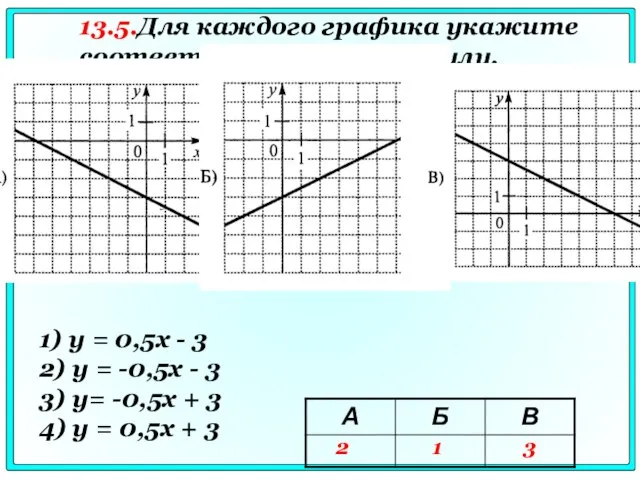
- 79. 1) у = 0,5х - 3 2) у = -0,5x - 3 3) y= -0,5x +
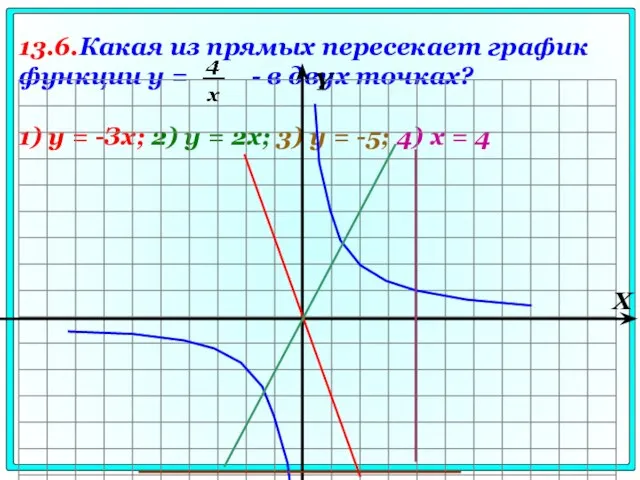
- 80. 13.6.Какая из прямых пересекает график функции у = - в двух точках? 1) у = -Зх;
- 81. Задача 14
- 82. 1 2a+12 2 3 4 Подумай Подумай Подумай Верно -3a-7 -2b+1 2a-1 14.1 Какое из приведенных
- 83. 1 3a+112 2 3 4 Подумай Подумай Верно Подумай 5a-1 12b-1 13a-102 14.2 Какое из приведенных
- 84. 1 5b-a>4b 2 3 4 Верно Подумай Подумай Подумай 5b-2a a-b 2a-2b>-1 14.3 Какое из приведенных
- 85. 1 b-3a 2 3 4 Подумай Подумай Верно Подумай 3b-3a>0 a-b+2>1 2a-5b>0 14.4 Какое из приведенных
- 86. 1 b-a 2 3 4 Подумай Подумай Верно Подумай 3a-b+1 -2b+2a>-1 5a-3b>0 14.4 Какое из приведенных
- 87. Задача 15
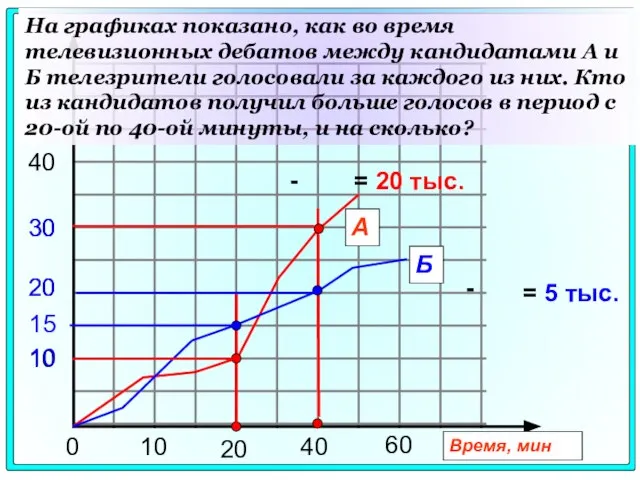
- 88. 0 10 20 40 10 20 30 А Б 40 Время, мин На графиках показано, как
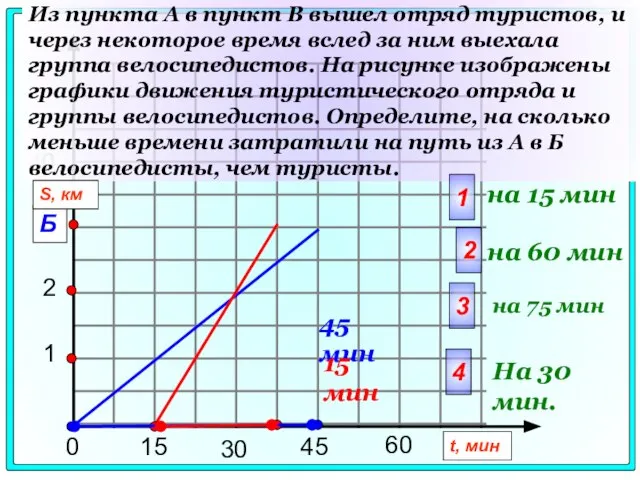
- 89. 0 15 30 45 1 Б 40 t, мин Из пункта А в пункт В вышел
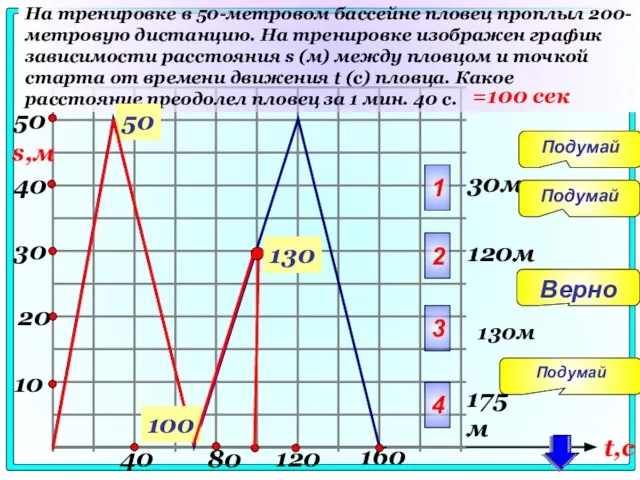
- 90. 40 10 30 20 40 80 120 160 На тренировке в 50-метровом бассейне пловец проплыл 200-метровую
- 91. Задача 16
- 92. Найдите a8. a2=a1+1=-1/a1=-3 a3=a2+1=-1/a2=-1/3 a4=a3+1=-1/a3=-3 ……………………….. a8=-3 16.1.Последовательность задана условиями:
- 93. 16.2 Геометрическая прогрессия задана условиями: b1=2; bn+1=-2bn. Какое из данных чисел является членом этой прогрессии? 1
- 94. 16.3 Про арифметическую прогрессию известно: a3=15; a7=23. Какое из данных чисел является членом этой прогрессии? 1
- 95. A xn = n2 Б В zn = 2n yn = 2n 16.4.Каждой последовательности, заданной формулой
- 96. Задания второй части
- 97. Задача 17
- 98. 17.1.a Сократите дробь. = = Разложим числитель способом группировки, а в знаменателе квадратный трехчлен на множители.
- 99. = = 17.1.b Сократите дробь. = = = - =
- 100. 17.2.a Упростите выражение. *Разложим в знаменателе второй дроби квадратный трехчлен на множители. + + ( )
- 101. + + 1) = (с+3) (с-2) = Разложим в числителе квадратный трехчлен на множители. 2с2+с-15=0 D=1+120=121
- 102. 2) • = = 17.2.б Упростите выражение. - • 1) = 2) - = =
- 103. Задача 18
- 104. 18.1.a Выясните, имеет ли корни уравнение: Уравнение имеет корни, если дискриминант неотрицателен: D≥0. a=1 b=2√2 +10
- 105. 18.1.b Выясните, имеет ли корни уравнение: D D= 4√6 -10 Уравнение не имеет корней.
- 106. 18.2.a Найдите область определения выражения: Область определения выражения задается условиями: Решим неравенство: 4+7x-2x2≥0 2x2-7x-4≤0 2x2-7x-4=0 D=a2-4ac=49-48=1
- 107. 18.2.b Найдите область определения выражения: [-1,5;1,5) U (1,5;2]
- 108. Задача 19
- 109. 19.1.a Найдите сумму всех натуральных чисел, не превосходящих 120, которые не делятся на 4. Пусть S
- 110. 19.2.b Найдите сумму всех натуральных чисел, не превосходящих 150, которые не делятся на 5. Найдем S1:
- 111. Задача 20
- 112. 20.1 Решите систему уравнений На основании условия равенства произведения нулю получим: или Решим первую систему. Из
- 113. 20.2 Решите систему уравнений На основании условия равенства произведения нулю получим: или Решим первую систему. Из
- 114. 20.3. Найдите все значения а, при которых неравенство х2 + (2а + 6)х + 12а +
- 115. 20.4. Найдите все значения а, при которых неравенство х2 -аx + a + 7 ≤ 0имеет
- 116. Задача 21
- 117. 21.1.a. Прямая у = -Зх + b касается окружности х2 + у2 = 10 в точке
- 118. 1) Найдем значения b, при которых система имеет единственное решение. Решение. Выполнив подстановку, получим уравнение х2
- 119. 3) Таким образом, получили уравнения двух прямых, касающихся окружности: у = —3х + 10 и у
- 120. 1) Найдем значения b, при которых система имеет единственное решение. Выполнив подстановку, получим уравнение х2 +
- 121. 3) Таким образом, получили уравнения двух прямых, касающихся окружности: у= 1/2x+ 5 и y= 1/2x- 5.
- 122. 21. Найдите все значения к, при которых прямая у = кх пересекает в трех различных точках
- 123. 1 1 0 Зх + 7, если х -2, если -3 3x — 11, если х
- 124. Прямая у = кх пересекает в трех различных точках этот график, если ее угловой коэффициент больше
- 125. 21. Найдите все значения к, при которых прямая у = кх пересекает в трех различных точках
- 127. Скачать презентацию


![1 2 3 4 [0,1; 0,2] [0,2; 0,3] [0,3; 0,4] [0,4; 0,5]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/442276/slide-3.jpg)






















































![18.2.b Найдите область определения выражения: [-1,5;1,5) U (1,5;2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/442276/slide-106.jpg)

















 Презентация на тему Правописание проверяемых букв согласных в корне слова
Презентация на тему Правописание проверяемых букв согласных в корне слова  Социальное служение Русской Православной Церкви
Социальное служение Русской Православной Церкви Отчёт по учебно-производственной практике. Специальность Ресторанное дело и гостиничный бизнес
Отчёт по учебно-производственной практике. Специальность Ресторанное дело и гостиничный бизнес Биологическое действие радиоактивных излучений. Защита организмов от них.
Биологическое действие радиоактивных излучений. Защита организмов от них. Дидактические игры как одна из активных форм обучения
Дидактические игры как одна из активных форм обучения На закате человеческой цивилизации появилась надежда…И была эта надежда в Московском институте открытого образования
На закате человеческой цивилизации появилась надежда…И была эта надежда в Московском институте открытого образования Окская тропа - 2018
Окская тропа - 2018 Математическое описание случайных явлений
Математическое описание случайных явлений Блины на масленницу
Блины на масленницу CMMI® for Acquisition: новая модель - для кого и зачем?
CMMI® for Acquisition: новая модель - для кого и зачем? Спорт, ребята, очень нужен
Спорт, ребята, очень нужен Положительные стороны занятий в секции спортивного ориентирования
Положительные стороны занятий в секции спортивного ориентирования Отраслевая структура мирового хозяйства. Воздействие НТР
Отраслевая структура мирового хозяйства. Воздействие НТР Презентация на тему угольная кислота и её соли 9 класс
Презентация на тему угольная кислота и её соли 9 класс  Вязание крючком
Вязание крючком 14 сентября 2011 да
14 сентября 2011 да Музей живой воды
Музей живой воды ЕВГЕНИЙ ИВАНОВИЧ ЧАРУШИН (1901-1965)
ЕВГЕНИЙ ИВАНОВИЧ ЧАРУШИН (1901-1965)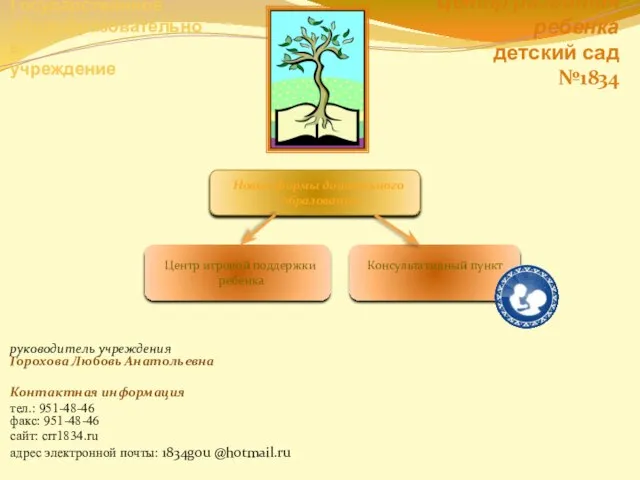 Центр развития ребенка детский сад №1834
Центр развития ребенка детский сад №1834 ОАО МЕТРОВАГОНМАШ
ОАО МЕТРОВАГОНМАШ Виктор Робертович Цой
Виктор Робертович Цой The Origins of English
The Origins of English  The observations of star formation regions by RT-22 PRAO ASC LPI - water maser sources survey. Lekht E.E. (1), Samodurov V.A. (2), Tolmachev A.M. (2) (1) Sternberg Astron.Inst. of MSU(2) PRAO ASC LPI
The observations of star formation regions by RT-22 PRAO ASC LPI - water maser sources survey. Lekht E.E. (1), Samodurov V.A. (2), Tolmachev A.M. (2) (1) Sternberg Astron.Inst. of MSU(2) PRAO ASC LPI Петербург – город мастеров кисти и резца
Петербург – город мастеров кисти и резца Домашняя Масленица
Домашняя Масленица Презентация
Презентация Сначала изучаем буквы в ряд )))))
Сначала изучаем буквы в ряд ))))) Современное стрелковое оружие
Современное стрелковое оружие