Содержание
- 2. Презентацию выполнила ученица 8 класса «Э» МОУ СОШ №34 Овсепян Карина Учитель : Гановичева А.Н. Список
- 3. Содержание Введение Задача о квадратуре круга Задача о трисекции угла Задача об удвоении куба Заключение
- 4. Введение Древним геометрам никак не удавалось выполнить некоторые построения, используя лишь циркуль и линейку, а построения,
- 5. Задача о квадратуре круга Одной из древнейших и самых популярных математических задач, занимавшей умы людей на
- 6. Задача о трисекции угла Рис.2 Знаменитой была в древности и задача о трисекции угла, т.е.о разделении
- 7. Попытки решения задачи с помощью инструментов и средств были предприняты еще в V в. до н.э.
- 8. Задача об удвоении куба Удвоение куба – так называется третья классическая задача древнегреческой математики. Эта задача
- 10. Скачать презентацию
Слайд 2 Презентацию выполнила
ученица 8 класса «Э»
МОУ СОШ №34
Овсепян Карина
Учитель
Презентацию выполнила
ученица 8 класса «Э»
МОУ СОШ №34
Овсепян Карина
Учитель

: Гановичева А.Н.
Список использованной литературы
Энц. «Большая серия знаний» 2002 год.
Философия: Учебник для высших учебных заведений. – Ростов н/Д.: «Феникс», 1998 – 576 с.
А также материалы сайтов
http://pirog13.narod.ru/i.htm
http://www.nips.riss-telecom.ru/poly/people
Список использованной литературы
Энц. «Большая серия знаний» 2002 год.
Философия: Учебник для высших учебных заведений. – Ростов н/Д.: «Феникс», 1998 – 576 с.
А также материалы сайтов
http://pirog13.narod.ru/i.htm
http://www.nips.riss-telecom.ru/poly/people
Слайд 3Содержание
Введение
Задача о квадратуре круга
Задача о трисекции угла
Задача об удвоении куба
Заключение
Содержание
Введение
Задача о квадратуре круга
Задача о трисекции угла
Задача об удвоении куба
Заключение

Слайд 4Введение
Древним геометрам никак не удавалось выполнить некоторые построения, используя лишь циркуль
Введение
Древним геометрам никак не удавалось выполнить некоторые построения, используя лишь циркуль
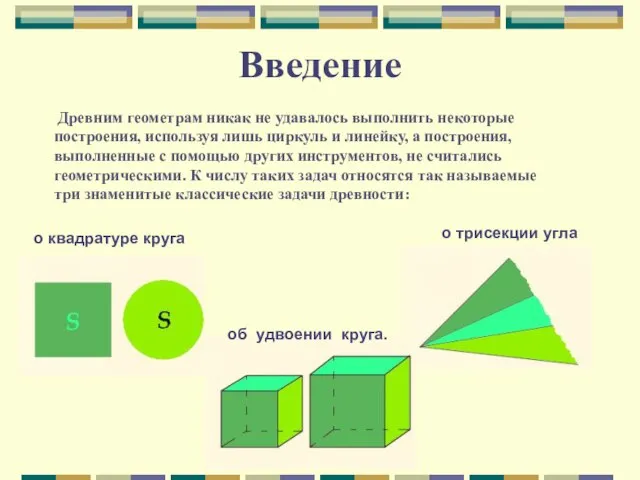
и линейку, а построения, выполненные с помощью других инструментов, не считались геометрическими. К числу таких задач относятся так называемые три знаменитые классические задачи древности:
об удвоении круга.
о трисекции угла
о квадратуре круга
Слайд 5Задача о квадратуре круга
Одной из древнейших и самых популярных математических задач,
Задача о квадратуре круга
Одной из древнейших и самых популярных математических задач,

занимавшей умы людей на протяжении 3 – 4 тысячелетий, является задача о квадратуре круга, т.е. о построении с помощью циркуля и линейки квадрата, равновеликому данному кругу. Один из современников Сократа – софист Антифон считал, что квадратуру круга можно осуществить следующим образом: впишем в круг квадрат и, разделяя пополам дуги, соответствующие его сторонам, построим правильный вписанный восьмиугольник, затем шестнадцати угольник и т.д., пока не получим многоугольник, который в силу малости сторон сольётся с окружностью. Но так как можно построить квадрат равновеликий любому многоугольнику, то и круг можно квадрировать. Однако уже Аристотель доказал, что это будет только приближённое, но не точное решение задачи, так как многоугольник никогда не может совпасть с кругом.
Слайд 6Задача о трисекции угла
Рис.2
Знаменитой была в древности и задача о трисекции
Задача о трисекции угла
Рис.2
Знаменитой была в древности и задача о трисекции

угла, т.е.о разделении угла на три равные части с помощью циркуля и линейки. Так, деление прямого угла на три равные части умели производить ещё пифагорейцы, основываясь на том, что в равностороннем треугольнике каждый угол равен 60о. Пусть требуется разделить на три равные части прямой угол MAN (Рис. 2). Откладываем на полупрямой произвольный отрезок , на котором строим равносторонний треугольник ACB. Так как угол Рис. 2 CAB равен 60о, то = 30о. Построим биссектрису угла САВ, получаем искомое деление прямого угла MAN на три равных угла: , , .
Задача о трисекции угла оказывается разрешимой и при некоторых других частных значениях угла , однако не в общем случае, т.е. любой угол невозможно разделить на три равных части с помощью только циркуля и линейки.
Задача о трисекции угла оказывается разрешимой и при некоторых других частных значениях угла , однако не в общем случае, т.е. любой угол невозможно разделить на три равных части с помощью только циркуля и линейки.
Слайд 7Попытки решения задачи с помощью инструментов и средств были предприняты еще в
Попытки решения задачи с помощью инструментов и средств были предприняты еще в
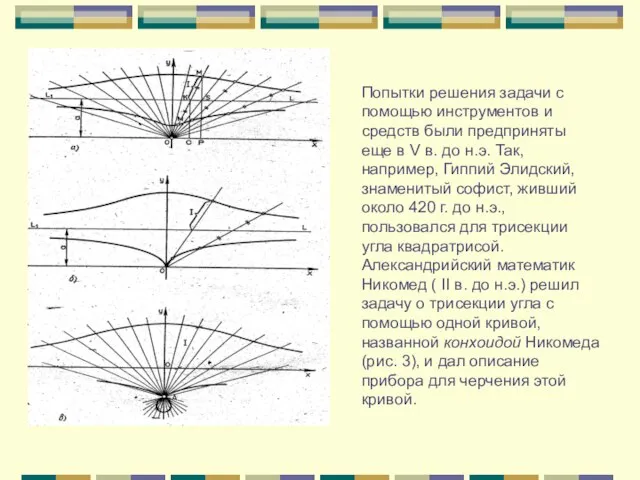
V в. до н.э. Так, например, Гиппий Элидский, знаменитый софист, живший около 420 г. до н.э., пользовался для трисекции угла квадратрисой. Александрийский математик Никомед ( II в. до н.э.) решил задачу о трисекции угла с помощью одной кривой, названной конхоидой Никомеда (рис. 3), и дал описание прибора для черчения этой кривой.
Слайд 8 Задача об удвоении куба
Удвоение куба – так называется третья классическая задача
Задача об удвоении куба
Удвоение куба – так называется третья классическая задача

древнегреческой математики. Эта задача на ряду с двумя первыми сыграла большую роль в развитии математических методов.
Задача состоит в построении куба, имеющий объём, вдвое больше объёма данного куба. Если обозначить через а ребро данного куба, то длина ребра х искомого куба должно удовлетворять уравнению
x³ = 2a³, или x =
Задача является естественным обобщением аналогичной задачей об удвоении квадрата, которая решается просто: стороной квадрата, площадь которого равна 2а², служит отрезок длиной а , т.е. диагональ данного квадрата со стороной а. Наоборот удвоение куба, объём которого равен 2а³, т.е. отрезок х, равный , не может быть построен при помощи циркуля и линейки. Однако это было доказано лишь в первой половине XIX в.
Задача состоит в построении куба, имеющий объём, вдвое больше объёма данного куба. Если обозначить через а ребро данного куба, то длина ребра х искомого куба должно удовлетворять уравнению
x³ = 2a³, или x =
Задача является естественным обобщением аналогичной задачей об удвоении квадрата, которая решается просто: стороной квадрата, площадь которого равна 2а², служит отрезок длиной а , т.е. диагональ данного квадрата со стороной а. Наоборот удвоение куба, объём которого равен 2а³, т.е. отрезок х, равный , не может быть построен при помощи циркуля и линейки. Однако это было доказано лишь в первой половине XIX в.
- Предыдущая
Автоматизация продаж Microsoft CRM МОУ «Журавская СОШ»
МОУ «Журавская СОШ» Мастер-класс по теме кофейная акварель
Мастер-класс по теме кофейная акварель Аннуитеты. Классификация аннуитетов
Аннуитеты. Классификация аннуитетов Презентация на тему Размножение и развитие животных (3 класс)
Презентация на тему Размножение и развитие животных (3 класс)  Семь смертных грехов в христианстве
Семь смертных грехов в христианстве Интерактивная игра типа Лабиринт Падежи
Интерактивная игра типа Лабиринт Падежи Когнитивно поведенческая терапия
Когнитивно поведенческая терапия Повышение информационно-коммуникационной компетентности педагогов
Повышение информационно-коммуникационной компетентности педагогов Роль инновационной образовательной программы в развитии социального партнерства
Роль инновационной образовательной программы в развитии социального партнерства  prezentatsiya-po-literature-emrachyov-illyustrator-basen-iakrylova-5-klass (2)
prezentatsiya-po-literature-emrachyov-illyustrator-basen-iakrylova-5-klass (2) Ащық сабақ. 27,11,2020
Ащық сабақ. 27,11,2020 Новое в содержании образовательных программ по предмету «Физическая культура» в соответствии с ФГОС второго поколения
Новое в содержании образовательных программ по предмету «Физическая культура» в соответствии с ФГОС второго поколения Подгузники Kidy
Подгузники Kidy День 3. Финансы. Накопление. Управление деньгами
День 3. Финансы. Накопление. Управление деньгами Бытовые нагревательные приборы и светильники: принцип действия и назначение. 8 класс
Бытовые нагревательные приборы и светильники: принцип действия и назначение. 8 класс Каталог. Фитиль ватный ТУ 8195-023-44881728-2016. Предназначен для парения, для подачи испаряемой жидкости к испарителю
Каталог. Фитиль ватный ТУ 8195-023-44881728-2016. Предназначен для парения, для подачи испаряемой жидкости к испарителю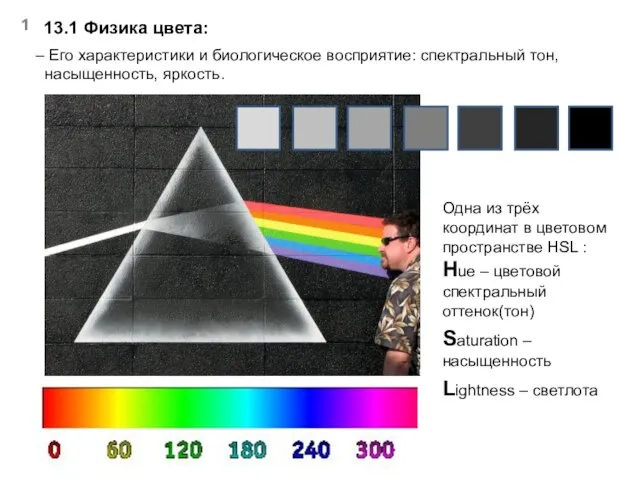 Физика цвета
Физика цвета Действительный член Ассоциации Международных Автомобильных Перевозчиков (АСМАП)
Действительный член Ассоциации Международных Автомобильных Перевозчиков (АСМАП) Презентация на тему Документы, предоставляемые при таможенном декларировании, их виды, примеры, оформление, применение
Презентация на тему Документы, предоставляемые при таможенном декларировании, их виды, примеры, оформление, применение  Публичный отчет МАОУ СОШ № 70
Публичный отчет МАОУ СОШ № 70 Музей боевой славы (Иркутск)
Музей боевой славы (Иркутск) Генераторные установки
Генераторные установки На фоне размещайте изображение
На фоне размещайте изображение Летняя практика. Зарисовки растений
Летняя практика. Зарисовки растений ТЕСТИРОВАНИЕ
ТЕСТИРОВАНИЕ Презентация на тему Периферическая нервная система
Презентация на тему Периферическая нервная система Презентация на тему о зимних Сочинских играх
Презентация на тему о зимних Сочинских играх Liguisan® A
Liguisan® A