Содержание
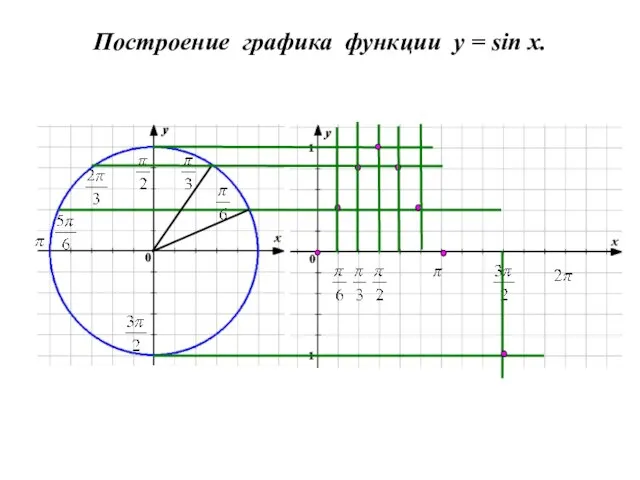
- 2. Построение графика функции y = sin x.
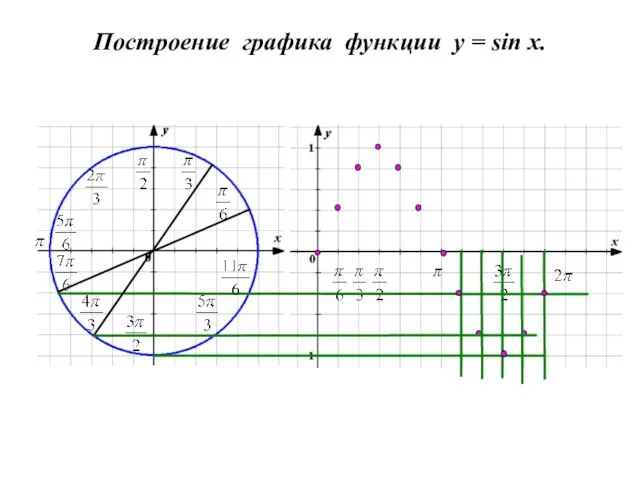
- 3. Построение графика функции y = sin x.
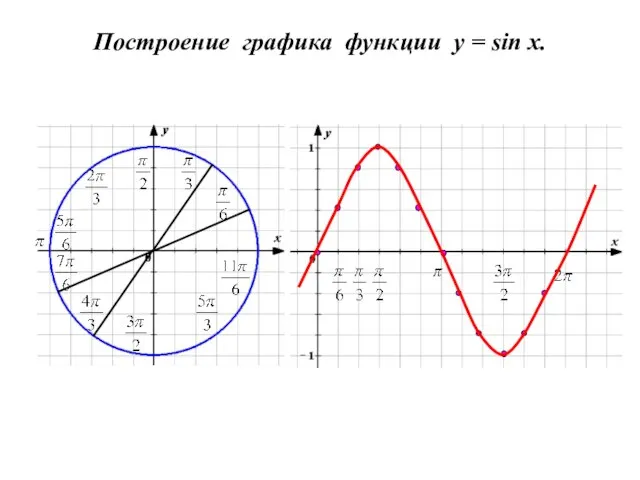
- 4. Построение графика функции y = sin x.
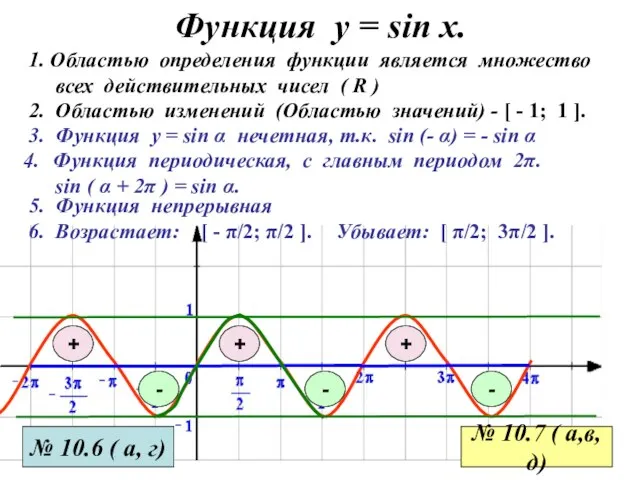
- 5. Функция у = sin x. 3. Функция у = sin α нечетная, т.к. sin (- α)
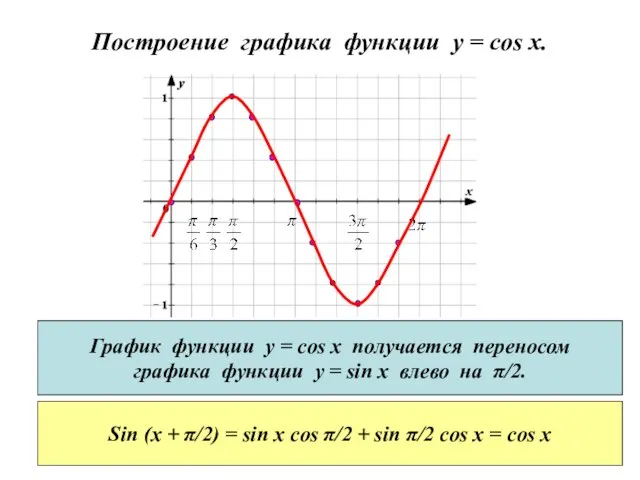
- 6. Построение графика функции y = cos x. График функции у = cos x получается переносом графика
- 8. Скачать презентацию
 Основные психологические феномены малой группы
Основные психологические феномены малой группы Презентация на тему Псориаз
Презентация на тему Псориаз начало ералаш
начало ералаш Античные образы в музыкальной культуре
Античные образы в музыкальной культуре Моя любимая игра волейбол
Моя любимая игра волейбол Балки составного сечения. Конструкция и расчёт
Балки составного сечения. Конструкция и расчёт Тема работы: "ИДЕНТИФИКАЦИЯ ИНДУКЦИОННОЙ ТИГЕЛЬНОЙ ПЕЧИ КАК ОБЪЕКТА УПРАВЛЕНИЯ С УЧЕТОМ ПЕРЕМЕННОГО УРОВНЯ РАСПЛАВА В ТИГЛЕ" Ра
Тема работы: "ИДЕНТИФИКАЦИЯ ИНДУКЦИОННОЙ ТИГЕЛЬНОЙ ПЕЧИ КАК ОБЪЕКТА УПРАВЛЕНИЯ С УЧЕТОМ ПЕРЕМЕННОГО УРОВНЯ РАСПЛАВА В ТИГЛЕ" Ра Апокалипсис – 2012 и новая энергетическая цивилизация
Апокалипсис – 2012 и новая энергетическая цивилизация Прежде чем приступать к разработке приложений средствами APEX, необходимо подготовить и настроить пространство для работы.
Прежде чем приступать к разработке приложений средствами APEX, необходимо подготовить и настроить пространство для работы. РУССКИЙ ЯЗЫК
РУССКИЙ ЯЗЫК Презентация на тему НАЛОГИ (шпаргалка)
Презентация на тему НАЛОГИ (шпаргалка) Основные сценарии использования мобильных платформ для работы с системами электронного документооборота: проблемы и поиск пут
Основные сценарии использования мобильных платформ для работы с системами электронного документооборота: проблемы и поиск пут Урок-игра в 8-Б классе Разработка Олейник И.Г.
Урок-игра в 8-Б классе Разработка Олейник И.Г. Проект “ПИРС”Педагогические Инновации – Реальная Стратегия
Проект “ПИРС”Педагогические Инновации – Реальная Стратегия Отряд Подёнки
Отряд Подёнки КВН
КВН Буквы З и С в приставках
Буквы З и С в приставках Метод проектов на уроке математики
Метод проектов на уроке математики Лидировать,развивая отношения
Лидировать,развивая отношения Сказка С. Маршака «Двенадцать месяцев»
Сказка С. Маршака «Двенадцать месяцев» Материал к педсовету ЕДИНЫЕ ТРЕБОВАНИЯ К ОБУЧАЮЩИМСЯ
Материал к педсовету ЕДИНЫЕ ТРЕБОВАНИЯ К ОБУЧАЮЩИМСЯ ДЕЯТЕЛЬНОСТЬ МЕТОДИЧЕСКОЙ СЛУЖБЫ
ДЕЯТЕЛЬНОСТЬ МЕТОДИЧЕСКОЙ СЛУЖБЫ День защиты детей
День защиты детей ТестМатематика 4 кл
ТестМатематика 4 кл 56 ДА! энергоэффективности
56 ДА! энергоэффективности Проект: Создание корпоративного информационно-образовательного Центра БФ ГОУ ВПО СибГУТИ Научный руководитель: Самсонов В.С., д
Проект: Создание корпоративного информационно-образовательного Центра БФ ГОУ ВПО СибГУТИ Научный руководитель: Самсонов В.С., д How bills become laws
How bills become laws Полупрямая
Полупрямая