Содержание
- 2. 1. Множество натуральных чисел сумма и произведение нат.чисел являются числами натуральными разность и частное – могут
- 3. 2. Множество целых чисел сумма, разность и произведение целых чисел всегда являются целыми числами частное –
- 4. 3. Множество рациональных чисел сумма, разность, произведение и частное (кроме деления на нуль) над рациональными числами
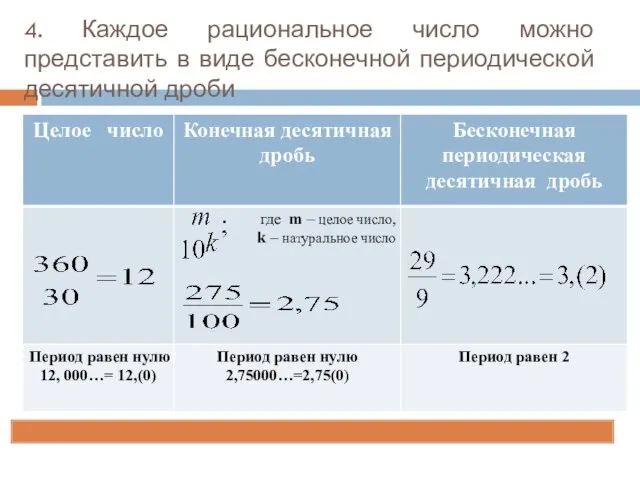
- 5. 4. Каждое рациональное число можно представить в виде бесконечной периодической десятичной дроби
- 6. №1. Запишите в виде десятичной дроби: Сверим ответы:
- 7. №2. Выполните действия и запишите результат в виде десятичной дроби: Сверим ответы:
- 8. 5. Справедливо и обратное утверждение: каждая бесконечная периодическая десятичная дробь является рациональным числом Рассмотрим задачу 2
- 9. №3(1,3,5,6). Записать в виде обыкновенной дроби бесконечную десятичную дробь: Сверим ответы: Далее №4; №5(1)
- 10. №3. Записать в виде обыкновенной дроби бесконечную десятичную дробь: Сверим ответы: Далее №4; №5(1) х= ко
- 11. №3. Записать в виде обыкновенной дроби бесконечную десятичную дробь: Сверим ответы: Далее №4; №5(1)
- 12. №3. Записать в виде обыкновенной дроби бесконечную десятичную дробь: Сверим ответы: Далее №4; №5(1)
- 13. = 4,75 Ответы:
- 14. Ответы:
- 15. ДОМАШНЯЯ РАБОТА. Глава1 , §1; 1(2,4,6) 10 класс 11 0,7272
- 16. Глава1 , §1; 2(2,4,6)
- 17. Глава1 , §1; 3(2,4) х = - 8/9
- 19. Скачать презентацию















 Евразия 4 класс
Евразия 4 класс Город будущего
Город будущего Рождество, да святки – ряженье, колядки.
Рождество, да святки – ряженье, колядки. Единая информационная база домашних животных и животных без владельцев
Единая информационная база домашних животных и животных без владельцев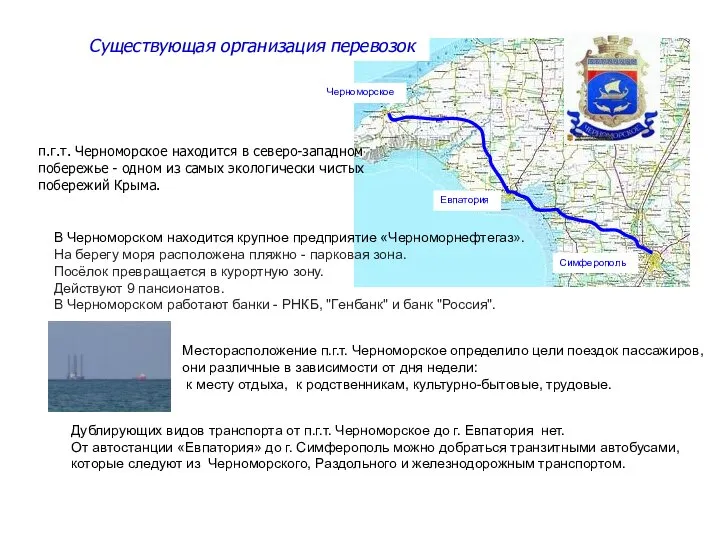 Существующая организация перевозок п.г.т. Черноморское
Существующая организация перевозок п.г.т. Черноморское Презентация на тему Разгром империи Наполеона. Венский конгресс (8 класс)
Презентация на тему Разгром империи Наполеона. Венский конгресс (8 класс) Классный час на тему:
Классный час на тему: Презентация на тему наклонения глагола
Презентация на тему наклонения глагола  404_A_N_D
404_A_N_D Сертификация СЭД на соответствие Закону «О персональных данных» Алексей Сидак, Центр безопасности информации Андрей Гриб, компан
Сертификация СЭД на соответствие Закону «О персональных данных» Алексей Сидак, Центр безопасности информации Андрей Гриб, компан Пейзаж
Пейзаж Анонимная сеть TOR
Анонимная сеть TOR Комплексный подход к работе с конверсией с помощью эконометрического моделирования
Комплексный подход к работе с конверсией с помощью эконометрического моделирования Хозяйство Руси и положение различных групп общества в XIV-XV вв
Хозяйство Руси и положение различных групп общества в XIV-XV вв Историческая школа в русской фольклористике
Историческая школа в русской фольклористике Осінні настрої
Осінні настрої Институт наук о Земле 2022
Институт наук о Земле 2022 Анализ финансового состояния в филиале ООО Авангард Цивильский бекон
Анализ финансового состояния в филиале ООО Авангард Цивильский бекон 9 класс МОУ «Сутчевская СОШ»
9 класс МОУ «Сутчевская СОШ» «СЕВЕРСТАЛЬ-УКРАИНА» — НАМ 5 ЛЕТ!
«СЕВЕРСТАЛЬ-УКРАИНА» — НАМ 5 ЛЕТ! Самоуправление
Самоуправление Презентация на классный час на тему_ Россия-страна возможностей_
Презентация на классный час на тему_ Россия-страна возможностей_ Электронный учебник Биография и педагогическое наследие Петра Францевича Лесгафта
Электронный учебник Биография и педагогическое наследие Петра Францевича Лесгафта Богатырский напиток, что силу и бодрость дает
Богатырский напиток, что силу и бодрость дает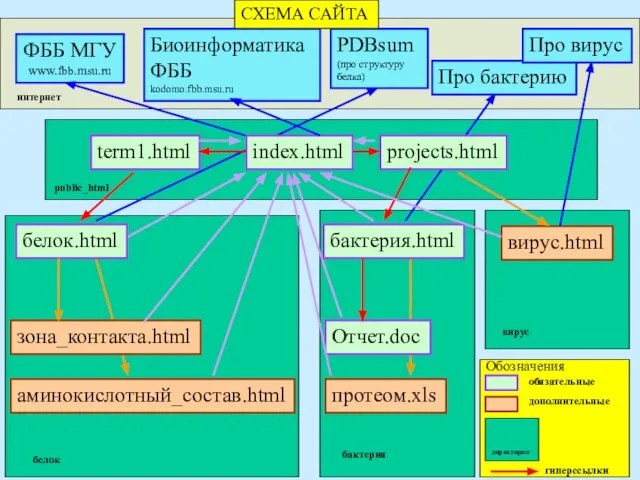 СХЕМА САЙТА
СХЕМА САЙТА Токарь
Токарь Герои, борцы, защитники. Изобразительное искусство
Герои, борцы, защитники. Изобразительное искусство Волшебный сундучок
Волшебный сундучок