УЧЕНЫЕ ИГРОМАНАМ

ТЕОРИЯ ВЕРОЯТНОСТЕЙ
«Неразрывно связана с нашей повседневной деятельностью»
У.Уивер
«Здравый смысл, сведенный к исчислению»
Лаплас
«Наука, изучающая закономерности массовых случайных явлений»
В.Афанасьев
«Вероятностные закономерности впервые были обнаружены в азартных играх»
М.Суворова

ГИПОТЕЗА
Если теория вероятностей появилась
благодаря появлению и развитию
азартных игр, то должен быть вклад
ученых в развитие теории азартных игр
ПРОБЛЕМНЫЙ ВОПРОС
За что игроманы должны благодарить науку?

ЦЕЛЬ: узнать имена ученых и их роль в развитии теории азартных
ЗАДАЧИ:
Узнать, что такое азартные игры, когда они появились
Кто из известных ученых имел отношение к азартным играм

Никколо Тарталья
(итальянский математик, 1499-1557)
Провел подсчет различных
комбинаций при игре в кости и
установил, что целесообразно
делать ставку на выпадение 7 очков
при бросании 2 костей;

Джироламо Кардано
(итальянский философ и врач, 1501-1576)
«Книга об игре в кости» (1526,
опубликована в 1663г.). Рассмтривал
многие задачи, связанные с бросанием 2 и
3 игральных костей. Предположил, что
азартные игры были изобретены
Галамедом во время десятилетней осады
Трои;

Галилео Галилей
(1564-1642)
«О выходе очков при игре в кости».
Привел исчерпывающее решение
задачи о числе возможных исходов
при одновременном бросании 3
игральных костей.

в частной переписке решали задачу, с
которой обратился к Блезу Паскалю
придворный французского короля
шевалье де Мере (1607 – 1648), сам
азартный игрок.
Блез Паскаль (Французский физик, математик, философ. 1623 – 1662)
Пьер Ферма
(французский математик, 1601-1665)

ЗАДАЧА ДЕ МОРЕ:
как справедливо разделить поставленные на кон деньги, если игроки прекратили игру преждевременно?
Лука Пачоли (итальянский математик) в 1494 предложил делить ставку пропорционально набранным очкам или партиям;
Джироламо Кардано предлагал делить ставку с учетом количества партий
Никколо Тарталья предлагал, что отклонение от половины ставки должно быть пропорциональноразности выигранных партий
Блез Паскаль рассматривал разные ситуации частных задач, и на основе изучения свойств таблицы биноминальных коэффициентов
Пьер Ферма составил таблицу возможных исходов

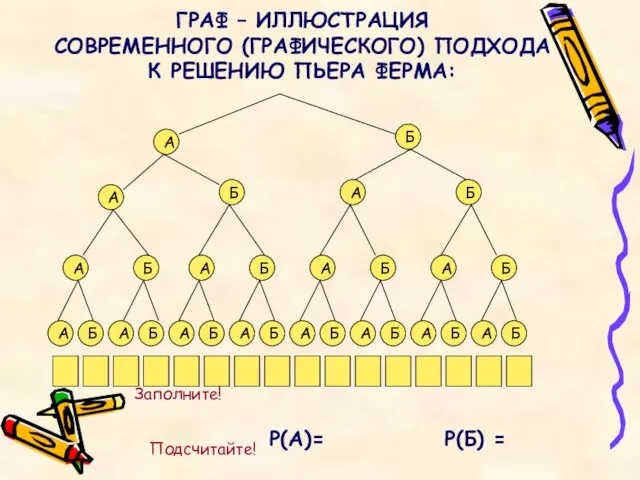
РЕШЕНИЕ ПЬЕРА ФЕРМА:
Пусть до выигрыша всей встречи игроку А недостает 2 партий, а игроку 3 партий. Как справедливо разделить ставку, если игра прервана?
Игра может быть продолжена максимум еще 4 партии
Число способов, которыми игра могла бы закончиться, не может быть одинаково вероятно
Возможные способы окончания серии игр с победой игрока А:
Победил, проиграл, победил, без разницы
Проиграл, победил, проиграл, победил
Победил, победил, без разницы, без разницы
Проиграл, проиграл и т.д.
Р(А)=11/16 Р(Б) = 5/16

ГРАФ – ИЛЛЮСТРАЦИЯ
СОВРЕМЕННОГО (ГРАФИЧЕСКОГО) ПОДХОДА
К РЕШЕНИЮ ПЬЕРА ФЕРМА:
А
А
Б
А
Б
А
Б
А
Б
А
Б
А
Б
А
Б
А
Б
А
Б
А
Б
А
Б
А
Б
А
Б
А
Б
Б
Р(А)= Р(Б) =
Заполните!
Подсчитайте!

ЗАДАЧА ГЮЙГЕНСА: трое игроков (А,В,С) по очереди извлекают по одному шару из урны, содержащей 5 белых и 3 черных шара. Побеждает тот, кто первым извлечет белый шар. Каким по счету выгоднее тянуть шар?
Р(А) = 5/8 + 3/8*2/7*1/6*5/5 = 36/56
Р (В) = 3/8*5/7 = 15/56
Р (C) = 3/8*2/7*5/6 = 5/56
Таким образом, если у игроков есть выбор, то выгоднее стоять первым, т.к. шансов на победу больше! НО 100% ГАРАНТИИ НЕТ!
5/8
5/7
5/6
5/5
3/8
2/7
1/6
А
В
С
А

ИТОГИ
Действительно, сначала появились азартные игры, а затем – вероятностные закономерности – теория вероятностей
Большое число ученых (математиков, физиков) занимались решением проблем, связанных с исходом азартных игр
Игроманы 15-17 вв обязаны науке своим успехом при выборе стратегии игры, при определении пропорции деления ставки при незаконченной игре