Угол между прямой и плоскостью

Повторяем теорию:
Как находят координаты вектора, если известны координаты его начала и конца?
Как находят координаты середины отрезка?
Как находят длину вектора?
Как находят расстояние между точками?
Как вы понимаете выражение «угол между векторами»?

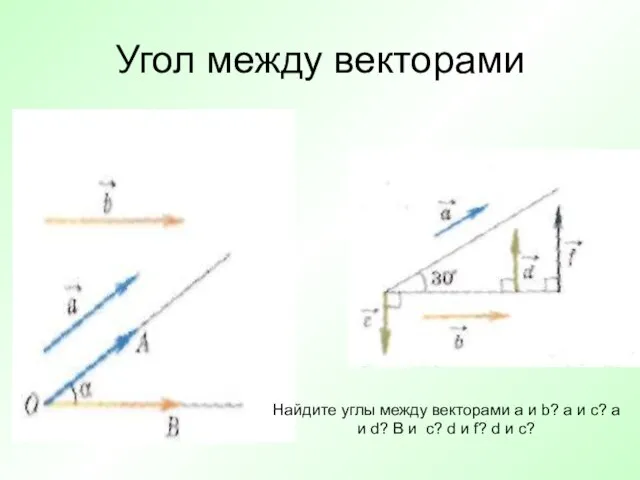
Угол между векторами
Найдите углы между векторами а и b? a и c? a и d? B и c? d и f? d и c?

Условие коллинеарности векторов:
Условие перпендикулярности векторов:
Какие векторы называются перпендикулярными?

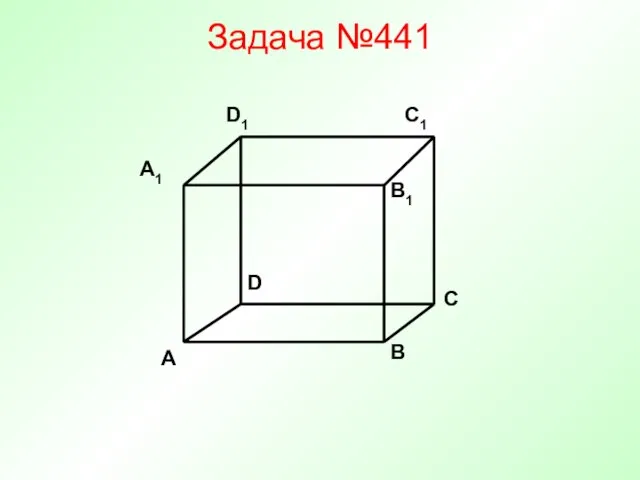
Задача №441

Повторяем теорию:
Что называется скалярным произведением векторов?
Чему равно скалярное произведение перпендикулярных векторов?
Чему равен скалярный квадрат вектора?
Свойства скалярного произведения?
0

Задача №444

Косинус угла между векторами

Задача №451(а)
Задача №453

Вычисление углов между прямыми и плоскостями
Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярную к ней, называют угол между прямой и её проекцией на плоскость.

1. Если a⊥α, то проекцией a на α является т. А
A=a∩α (a,α)=90°
2. Если a||α, a1 - проекция a на α, то a||a1, a1⊂α. (a,α)=0°

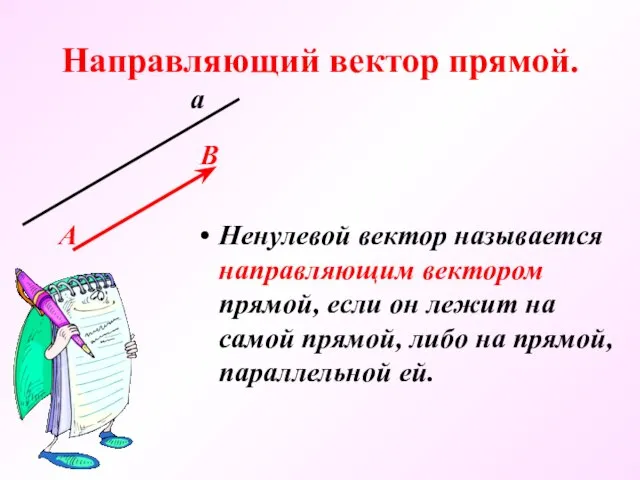
Направляющий вектор прямой.
Ненулевой вектор называется направляющим вектором прямой, если он лежит на самой прямой, либо на прямой, параллельной ей.
а
В
А

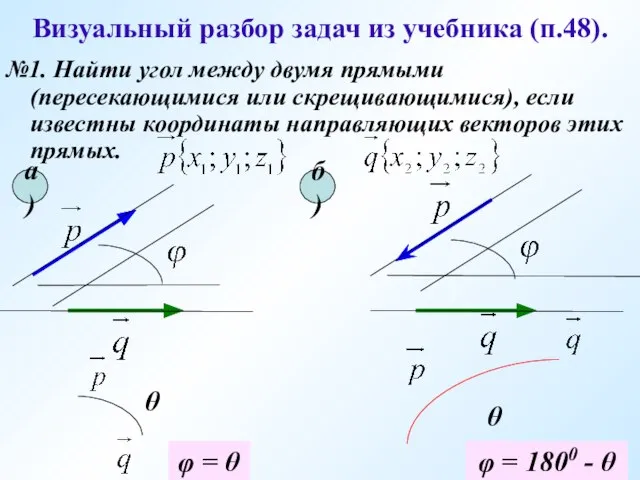
Визуальный разбор задач из учебника (п.48).
№1. Найти угол между двумя прямыми (пересекающимися или скрещивающимися), если известны координаты направляющих векторов этих прямых.
а)
б)
θ
θ
φ = θ
φ = 1800 - θ

Ответ:

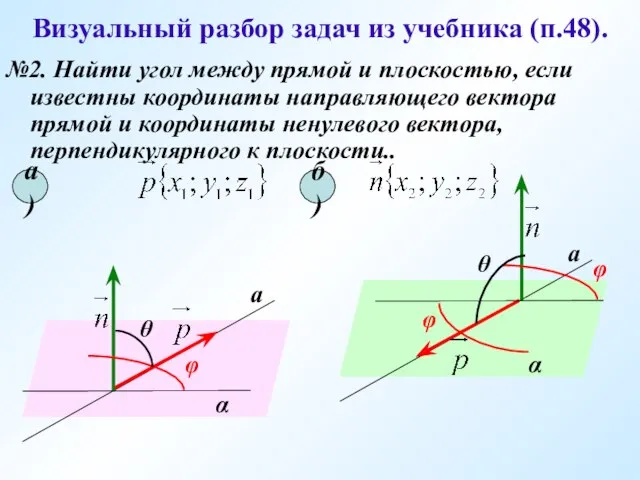
Визуальный разбор задач из учебника (п.48).
№2. Найти угол между прямой и плоскостью, если известны координаты направляющего вектора прямой и координаты ненулевого вектора, перпендикулярного к плоскости..
а)
б)
α
а
φ
θ
α
а
φ
φ
θ

№ 464 (а)
Дано:
Найти: угол между прямыми АВ и CD.
Ваши предложения…
Найдем координаты векторов
и
2. Воспользуемся формулой:
φ = 300

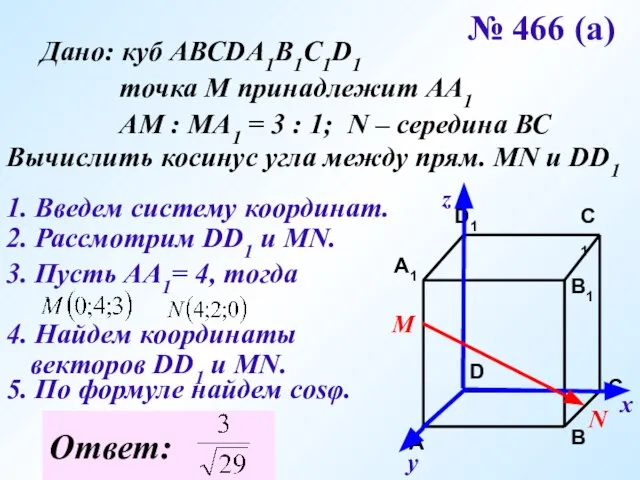
№ 466 (а)
Дано: куб АВСDA1B1C1D1
точка М принадлежит АА1
АМ : МА1 = 3 : 1; N – середина ВС
Вычислить косинус угла между прям. MN и DD1
1. Введем систему координат.
х
у
z
2. Рассмотрим DD1 и МN.
М
N
3. Пусть АА1= 4, тогда
4. Найдем координаты векторов DD1 и MN.
5. По формуле найдем cosφ.
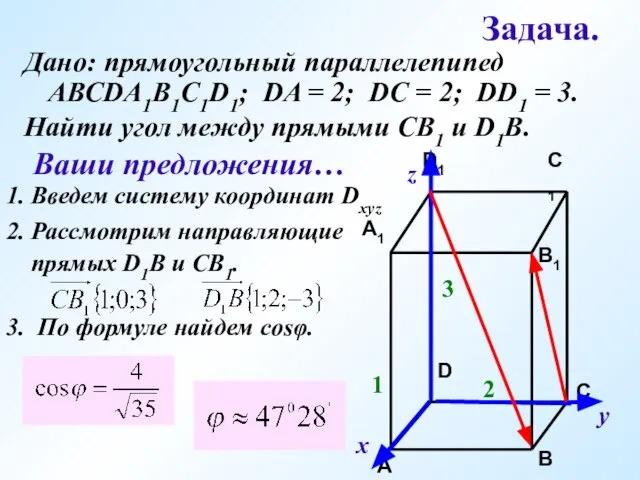
Ответ:

Задача.
Дано: прямоугольный параллелепипед АВСDA1B1C1D1; DA = 2; DC = 2; DD1 = 3.
1
2
3
Найти угол между прямыми СВ1 и D1B.
х
у
z
Ваши предложения…
1. Введем систему координат Dxyz
2. Рассмотрим направляющие
прямых D1B и CB1.
3. По формуле найдем cosφ.

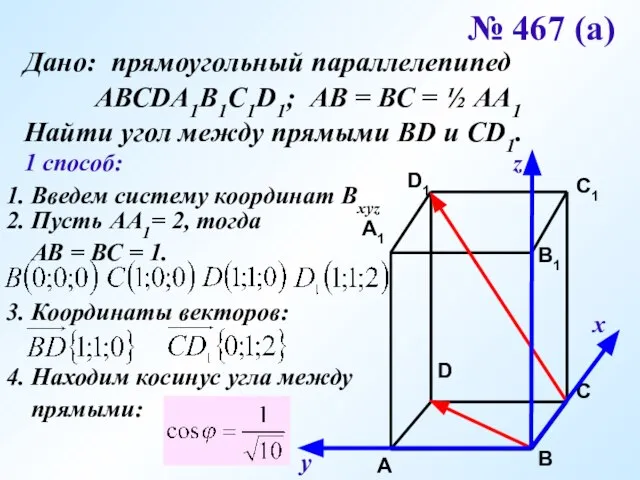
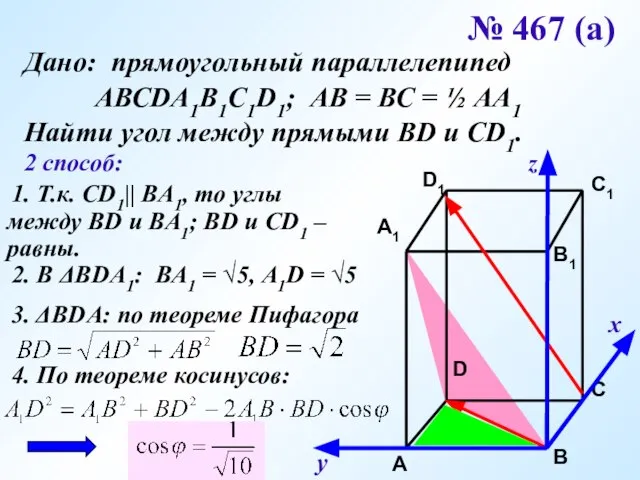
№ 467 (а)
Дано: прямоугольный параллелепипед
АВСDA1B1C1D1; АВ = ВС = ½ АА1
Найти угол между прямыми ВD и CD1.
1 способ:
1. Введем систему координат Bxyz
х
у
z
2. Пусть АА1= 2, тогда
АВ = ВС = 1.
3. Координаты векторов:
4. Находим косинус угла между
прямыми:

х
у
z
№ 467 (а)
Дано: прямоугольный параллелепипед
АВСDA1B1C1D1; АВ = ВС = ½ АА1
Найти угол между прямыми ВD и CD1.
2 способ:
1. Т.к. СD1|| ВА1, то углы между ВD и ВА1; ВD и СD1 – равны.
2. В ΔВDА1: ВА1 = √5, А1D = √5
3. ΔВDА: по теореме Пифагора
4. По теореме косинусов: