Уникурсальный граф

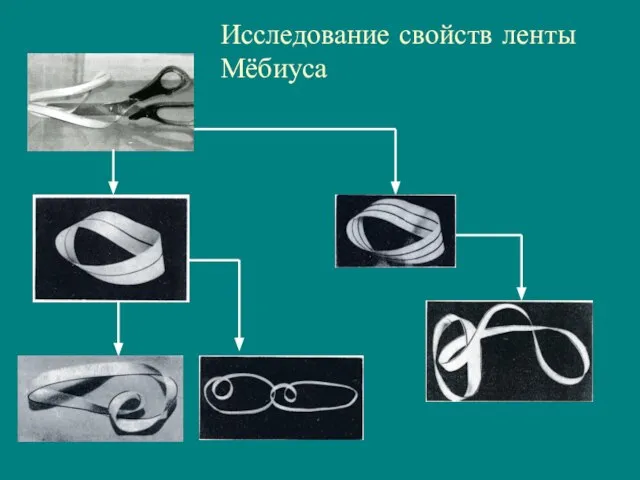
Исследование свойств ленты Мёбиуса

Задача не решается, и это тем досаднее, что она не решается только «чуть-чуть»...

Выпуклый пятиугольник со всеми его диагоналями легко вычерчивается одним непрерывным движением без повторения.

исследование, возможна или нет данная задача- головоломка, прежде чем приниматься за её решение.
Проблема:

Гипотеза :
свойство графа быть уникурсальным – есть способ определения возможности решения задач

Объект
исследования:
уникурсальный граф как фигура, вычерчиваемая одним росчерком.
Предмет
исследования:
топологическое свойство графа быть уникурсальным и его использование для решения задач – головоломок

Цель работы :
определить и опытно-экспериментальным путём проверить свойство уникурсального графа и его использование для решения задач-головоломок

Задачи :
- раскрыть понятие топологии;
-изучить вклад Л.Эйлера в развитие науки топологии
- дать представление об уникурсальном графе и привести доказательство его топологического свойства
- проверить опытно-экспериментальным путем возможность использования свойства для решения задач-головоломок

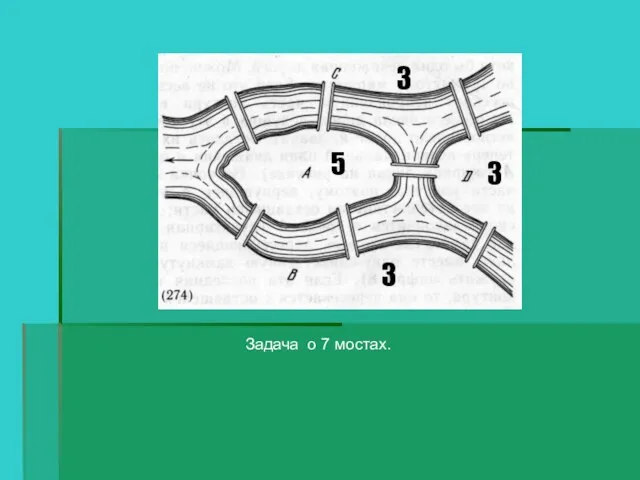
Задача о 7 мостах.
5
3
3
3

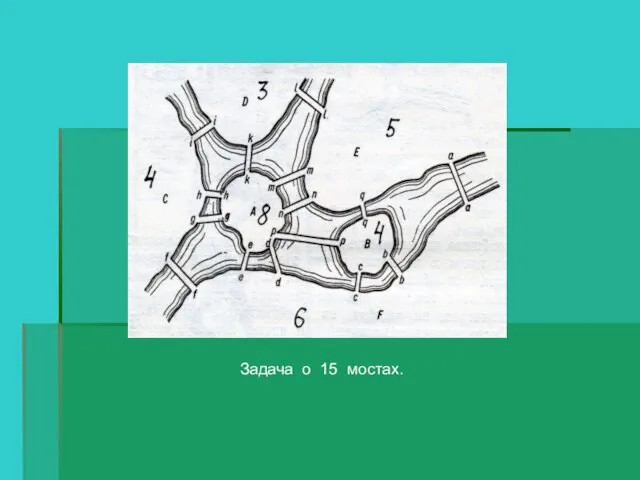
Задача о 15 мостах.

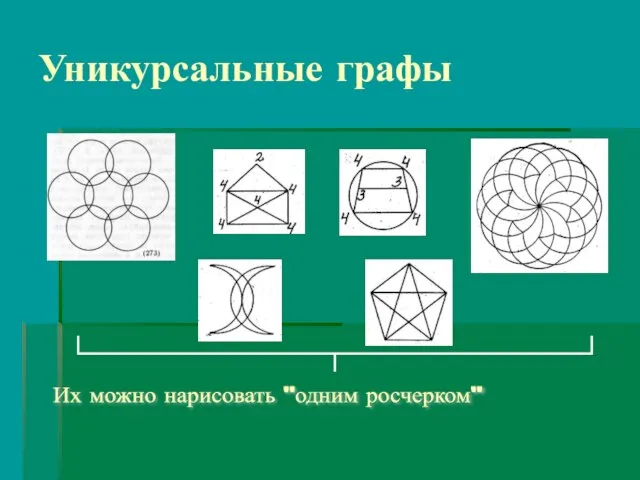
Уникурсальные графы
Их можно нарисовать "одним росчерком"

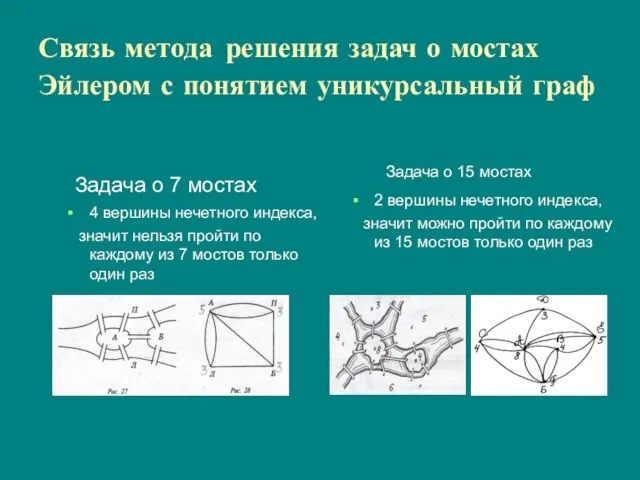
Связь метода решения задач о мостах Эйлером с понятием уникурсальный граф
Задача о 7 мостах
4 вершины нечетного индекса,
значит нельзя пройти по каждому из 7 мостов только один раз
Задача о 15 мостах
2 вершины нечетного индекса,
значит можно пройти по каждому из 15 мостов только один раз

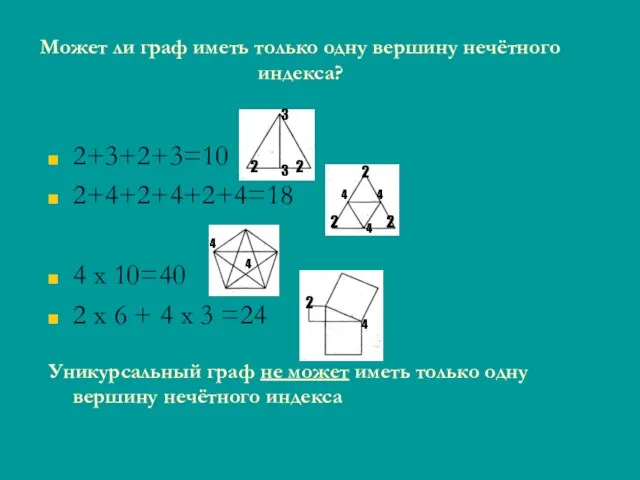
Может ли граф иметь только одну вершину нечётного индекса?
2+3+2+3=10
2+4+2+4+2+4=18
4 x 10=40
2 x 6 + 4 x 3 =24
Уникурсальный граф не может иметь только одну вершину нечётного индекса
3
3
2
2
2
2
2
4
4
4
4
4
4
2

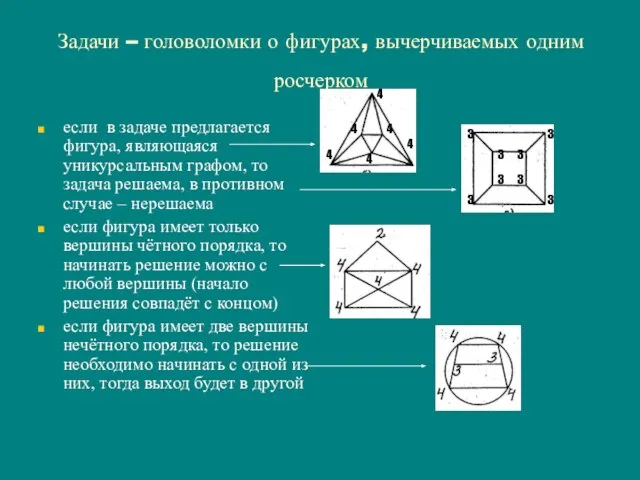
Задачи – головоломки о фигурах, вычерчиваемых одним росчерком
если в задаче предлагается фигура, являющаяся уникурсальным графом, то задача решаема, в противном случае – нерешаема
если фигура имеет только вершины чётного порядка, то начинать решение можно с любой вершины (начало решения совпадёт с концом)
если фигура имеет две вершины нечётного порядка, то решение необходимо начинать с одной из них, тогда выход будет в другой
4
4
4
4
4
4
3
3
3
3
3
3
3
3

Заключение
Результаты исследования показали, что гипотеза верна:
свойство графа быть уникурсальным является способом определения возможности решения задачи-головоломки

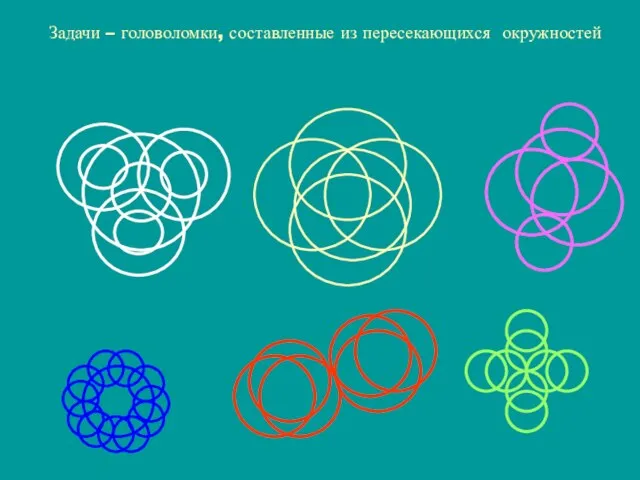
Задачи – головоломки, составленные из пересекающихся окружностей

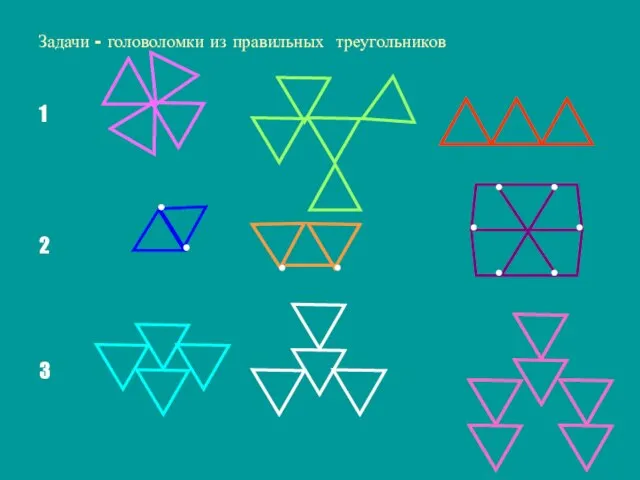
Задачи - головоломки из правильных треугольников
1
2
3

Задачи - головоломки из правильных треугольников