Упругие напряжения и псевдоморфизм в гетероэпитаксиальных структурах

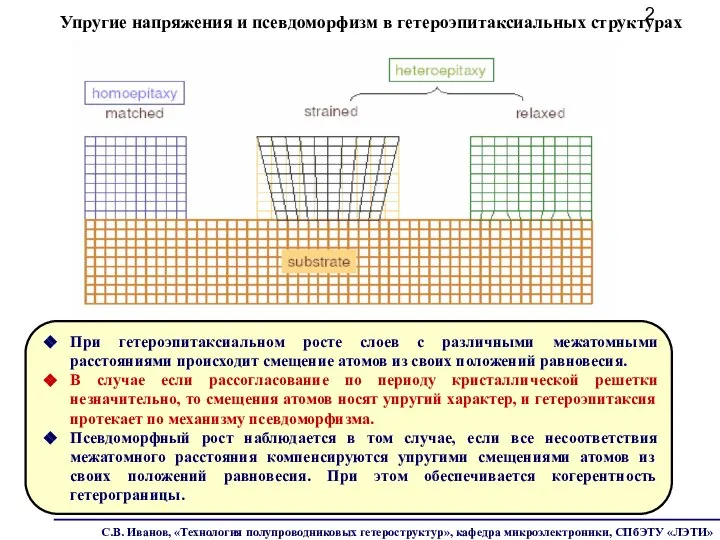
Упругие напряжения и псевдоморфизм в гетероэпитаксиальных структурах
При гетероэпитаксиальном росте слоев с различными межатомными расстояниями происходит смещение атомов из своих положений равновесия.
В случае если рассогласование по периоду кристаллической решетки незначительно, то смещения атомов носят упругий характер, и гетероэпитаксия протекает по механизму псевдоморфизма.
Псевдоморфный рост наблюдается в том случае, если все несоответствия межатомного расстояния компенсируются упругими смещениями атомов из своих положений равновесия. При этом обеспечивается когерентность гетерограницы.

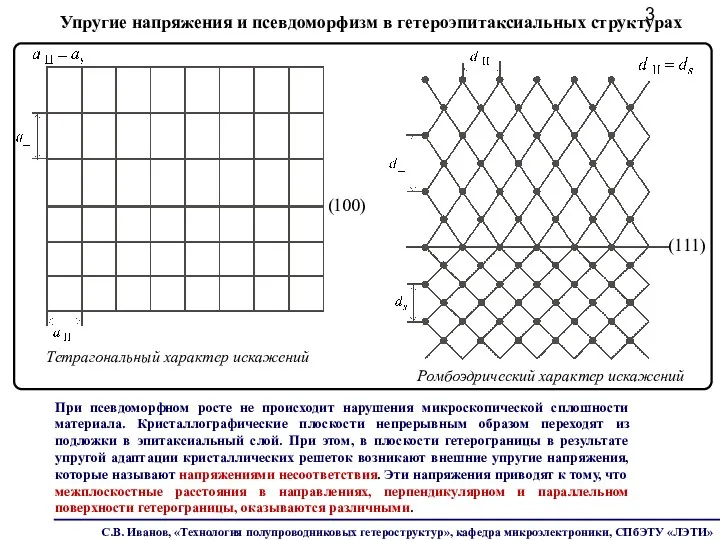
(111)
Ромбоэдрический характер искажений
Тетрагональный характер искажений
Упругие напряжения и псевдоморфизм в гетероэпитаксиальных структурах
При псевдоморфном росте не происходит нарушения микроскопической сплошности материала. Кристаллографические плоскости непрерывным образом переходят из подложки в эпитаксиальный слой. При этом, в плоскости гетерограницы в результате упругой адаптации кристаллических решеток возникают внешние упругие напряжения, которые называют напряжениями несоответствия. Эти напряжения приводят к тому, что межплоскостные расстояния в направлениях, перпендикулярном и параллельном поверхности гетерограницы, оказываются различными.

Характер упругих искажений кристаллической решетки при псевдоморфном росте
(100)
При псевдоморфном росте подложка навязывает свой период формируемому эпитаксиальному слою
Кристаллические решетки псевдоморфных фаз когерентно рассеивают акустические, оптические и рентгеновские лучи
Основной признак когерентности гетерограницы
Упругие напряжения и псевдоморфизм в гетероэпитаксиальных структурах

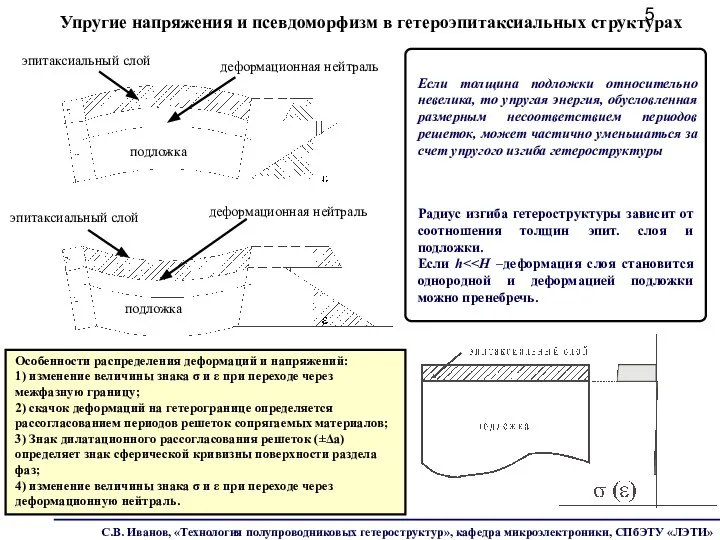
Особенности распределения деформаций и напряжений:
1) изменение величины знака σ и ε при переходе через межфазную границу;
2) скачок деформаций на гетерогранице определяется рассогласованием периодов решеток сопрягаемых материалов;
3) Знак дилатационного рассогласования решеток (±Δa) определяет знак сферической кривизны поверхности раздела фаз;
4) изменение величины знака σ и ε при переходе через деформационную нейтраль.
Радиус изгиба гетероструктуры зависит от соотношения толщин эпит. слоя и подложки.
Если h<
Если толщина подложки относительно невелика, то упругая энергия, обусловленная размерным несоответствием периодов решеток, может частично уменьшаться за счет упругого изгиба гетероструктуры
Упругие напряжения и псевдоморфизм в гетероэпитаксиальных структурах

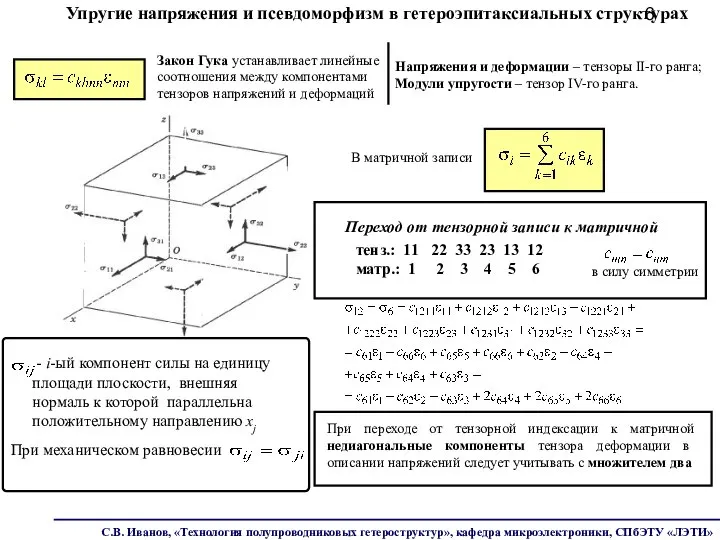
Упругие напряжения и псевдоморфизм в гетероэпитаксиальных структурах
При механическом равновесии
- i-ый компонент силы на единицу площади плоскости, внешняя нормаль к которой параллельна положительному направлению xj
Закон Гука устанавливает линейные соотношения между компонентами тензоров напряжений и деформаций
Напряжения и деформации – тензоры II-го ранга;
Модули упругости – тензор IV-го ранга.
В матричной записи
Переход от тензорной записи к матричной
тенз.: 11 22 33 23 13 12
матр.: 1 2 3 4 5 6
в силу симметрии
При переходе от тензорной индексации к матричной недиагональные компоненты тензора деформации в описании напряжений следует учитывать с множителем два

Закон Гука в применении к деформированным гетероструктурам
Закон Гука
Переход от тензорной записи к матричной
тенз.: 11 22 33 23 13 12
матр.: 1 2 3 4 5 6
в силу симметрии
При переходе от тензорной индексации к матричной недиагональные компоненты тензора деформации в описании напряжений следует учитывать с множителем два
Вид тензора модуля упругости зависит от симметрии кристалла и кристаллографической ориентации гетероструктуры

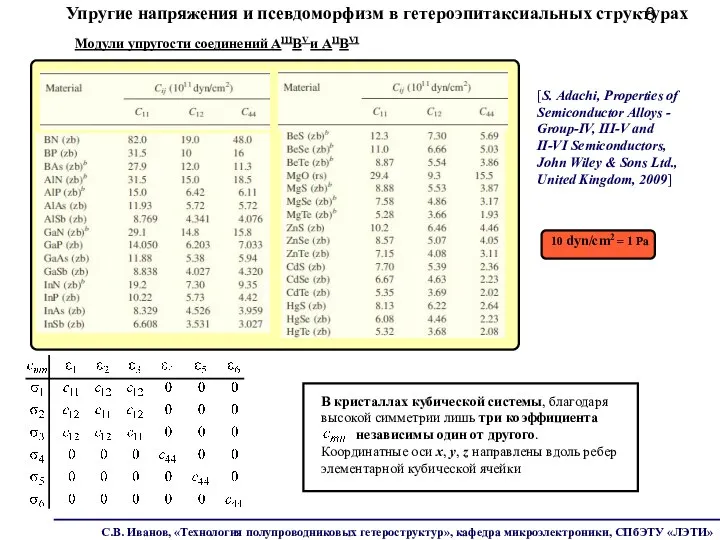
Упругие напряжения и псевдоморфизм в гетероэпитаксиальных структурах
Модули упругости соединений AIIIBV и AIIBVI
[S. Adachi, Properties of Semiconductor Alloys - Group-IV, III-V and II-VI Semiconductors, John Wiley & Sons Ltd., United Kingdom, 2009]
10 dyn/cm2 = 1 Pa

Для полупроводников AIIIBV и AIIBVI
Закон Гука в применении к деформированным гетероструктурам
При ориентации слоя в плоскости (100)
Экспериментально измеряемое различие периодов решеток подложки и слоя в направлении нормали к границе раздела приблизительно в два раза превосходит несоответствие периодов решеток этих материалов в недеформированном состоянии
В плоскости слоя нормальные напряжения одинаковы ,
а касательные напряжения отсутствуют
Индексы 1, 2 и 3 соответствуют осям x, y, z.
По направлению нормали к плоскости гетероструктуры, т.е. вдоль оси z ,
эпитаксиальная структура ненагружена, поэтому ,
однако деформация отлична от нуля.
(направление роста совпадает с осью z )

Закон Гука в применении к деформированным гетероструктурам
Плотность упругой энергии для кубических кристаллов:
При ориентации слоя в плоскости (111)
(направление роста совпадает с z/ )
Для расчета деформаций и напряжений в этом случае целесообразно перейти к основной координатной системе, в которой нормальные и сдвиговые напряжения совпадают с направлениями {100}
По отношению к направлениям {111} оси x, y, z кристалло-графически эквивалентны. Благодаря симметрии имеем:

Закон Гука в применении к деформированным гетероструктурам
Правило преобразования компонент тензоров при переходе из одной системы координат в другую:
Для преобразования координатной системы сначала осуществляем поворот осей x и y вокруг оси z на 45º (в плоскости xy), а затем оси z/ и x/ поворачиваем вокруг оси y/ на 45º
тенз.: 11 22 33 23 13 12
матр.: 1 2 3 4 5 6

Закон Гука в применении к деформированным гетероструктурам

Закон Гука в применении к деформированным гетероструктурам

Пример расчета деформированного состояния гетероструктуры
Система ZnSySe1-y/GaAs (001)
TS=300°C, x=0.06
Характеристики эпит. слоя:
TS=300K
Химически обусловленное несоответствие решеток:
Рассогласование периодов решеток вдоль
нормали к гетерогранице:
Упругая деформация в плоскости гетерограницы:
Упругая деформация в направлении роста:
Упругие напряжения в плоскости слоя:
(напряжения сжатия)

Пример расчета деформированного состояния гетероструктуры
Система ZnSySe1-y/GaAs (001)
TS=300°C, x=0.06
Характеристики эпит. слоя:
TS=300°C (температура эпитаксии)

Пример расчета деформированного состояния гетероструктуры
Система GaxIn1-xP/GaAs(111)
TS=800°C, x=0.5
Характеристики эпит. слоя:
TS=300K
Химически обусловленное несоответствие решеток:
Рассогласование периодов решеток вдоль нормали к гетерогранице:
Упругая деформация в плоскости гетерограницы:
Упругая деформация в направлении роста:
Упругие напряжения в плоскости слоя:
TS=800°C (температура эпитаксии)
(напряжения сжатия)

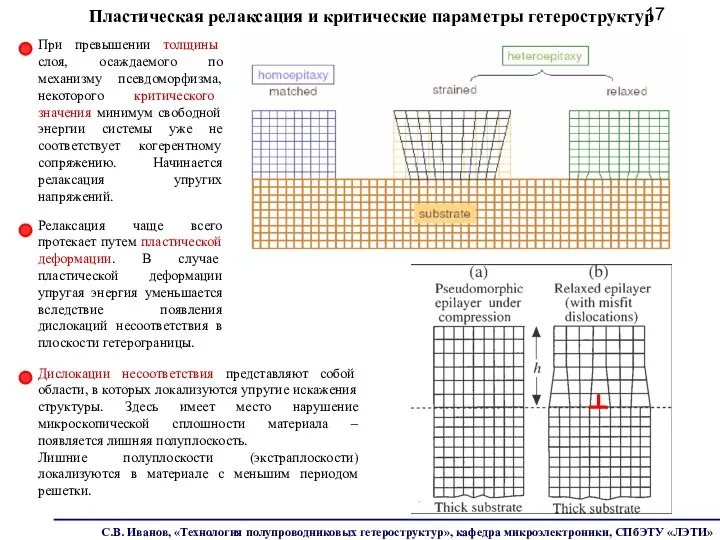
Пластическая релаксация и критические параметры гетероструктур
При превышении толщины слоя, осаждаемого по механизму псевдоморфизма, некоторого критического значения минимум свободной энергии системы уже не соответствует когерентному сопряжению. Начинается релаксация упругих напряжений.
Релаксация чаще всего протекает путем пластической деформации. В случае пластической деформации упругая энергия уменьшается вследствие появления дислокаций несоответствия в плоскости гетерограницы.
Дислокации несоответствия представляют собой области, в которых локализуются упругие искажения структуры. Здесь имеет место нарушение микроскопической сплошности материала – появляется лишняя полуплоскость.
Лишние полуплоскости (экстраплоскости) локализуются в материале с меньшим периодом решетки.

(100)
Контур Бюргерса всегда замкнут
Контур Бюргерса
Совершенный кристалл:
Пластическая релаксация и критические параметры гетероструктур
Контур Бюргерса – замкнутый контур произвольной формы, построенный в реальном кристалле путем последовательного обхода дефекта от атома к атому в совершенной области кристалла.
Вектор Бюргерса, замыкающий контур в несовершенном кристалле, является мерой искажения решетки, которое вызвано дислокацией. Величина вектора Бюргерса не зависит от того, насколько контур Бюргерса удален от дислокации.
Чем дальше от дислокации мы располагаем этот контур, тем меньше упругие смещения атомов в совершенной области, но тем длиннее контур, и сумма всех упругих смещений, накопившаяся при его обходе, остается постоянной.
Вектор Бюргерса для контура, замыкающегося вокруг нескольких дислокаций, равен сумме векторов Бюргерса отдельных дислокаций.

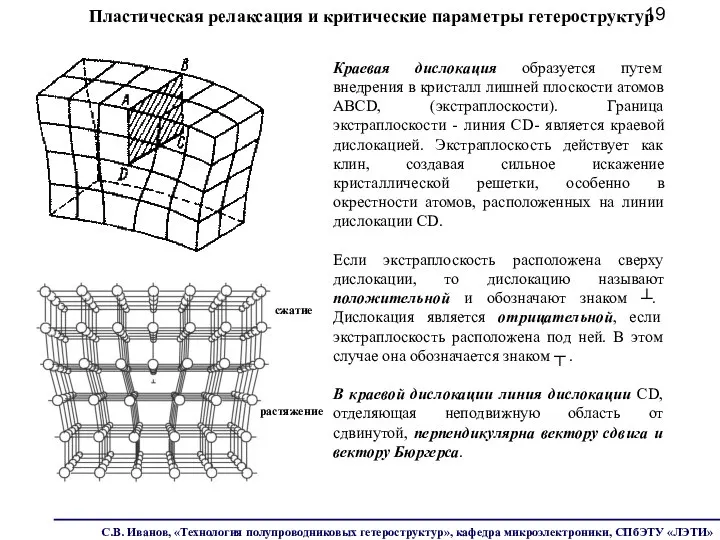
Краевая дислокация образуется путем внедрения в кристалл лишней плоскости атомов ABCD, (экстраплоскости). Граница экстраплоскости - линия CD- является краевой дислокацией. Экстраплоскость действует как клин, создавая сильное искажение кристаллической решетки, особенно в окрестности атомов, расположенных на линии дислокации CD.
Если экстраплоскость расположена сверху дислокации, то дислокацию называют положительной и обозначают знаком ┴. Дислокация является отрицательной, если экстраплоскость расположена под ней. В этом случае она обозначается знаком ┬ .
В краевой дислокации линия дислокации CD, отделяющая неподвижную область от сдвинутой, перпендикулярна вектору сдвига и вектору Бюргерса.
Пластическая релаксация и критические параметры гетероструктур
сжатие
растяжение

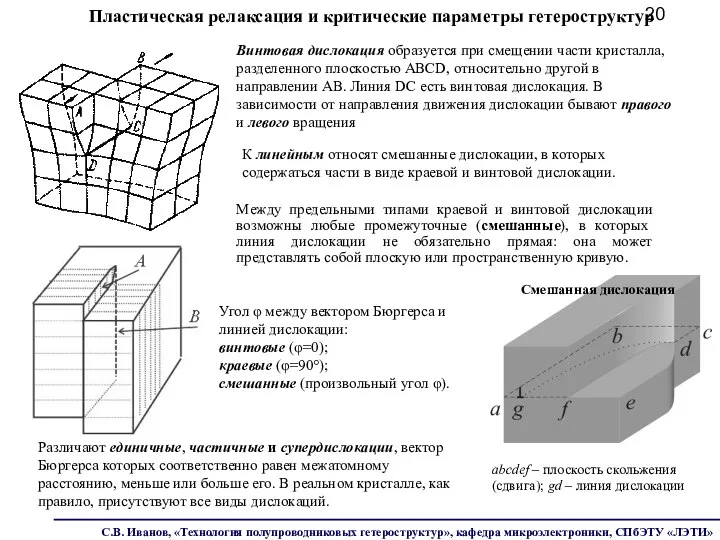
Винтовая дислокация образуется при смещении части кристалла, разделенного плоскостью ABCD, относительно другой в направлении АВ. Линия DC есть винтовая дислокация. В зависимости от направления движения дислокации бывают правого и левого вращения
К линейным относят смешанные дислокации, в которых содержаться части в виде краевой и винтовой дислокации.
Пластическая релаксация и критические параметры гетероструктур
abcdef – плоскость скольжения (сдвига); gd – линия дислокации
Между предельными типами краевой и винтовой дислокации возможны любые промежуточные (смешанные), в которых линия дислокации не обязательно прямая: она может представлять собой плоскую или пространственную кривую.
Угол φ между вектором Бюргерса и линией дислокации:
винтовые (φ=0);
краевые (φ=90°);
смешанные (произвольный угол φ).
Смешанная дислокация
Различают единичные, частичные и супердислокации, вектор Бюргерса которых соответственно равен межатомному расстоянию, меньше или больше его. В реальном кристалле, как правило, присутствуют все виды дислокаций.

Принято считать, что устранение дилатационного несоответствия вдоль каждого направления в гетерогранице происходит независимым образом. Экспериментальным подтверждением этого тезиса является образование плоской дислокационной сетки в реальных гетероструктурах.
В п/п AIIIBV (ГЦК решетка) плоскостями скольжения являются плоскости семейства {111}. Дилатационное несоответствие на границах раздела фаз типа (100) в гранецентрированных кристаллах компенсируется двумя взаимно перпендикулярными системами краевых дислокаций, а при гетероэпитаксии на подложках (111) образуется гексагональная сетка ДН.
При наличии ДН в плоскости гетерограницы имеет место неоднородное распределение напряжений
Пластическая релаксация и критические параметры гетероструктур
Геометрический тип сетки дислокаций определяется расположением плоскостей скольжения кристалла относительно плоскости границы раздела.
При деформационном равновесии ДН вдоль выбранного направления в границе раздела расположены эквидистантно, на расстояниях, обратно пропорциональных величине рассогласования решеток.
Плоскостями скольжения обычно являются наиболее плотно-упакованные плоскости, расстояние между которыми максимально
Образование ДН является термически активированным процессом
ПЭМ изображение гетероинтерфейса ZnSe/GaAs,
демонстрирующее эволюцию сетки ДН с увеличением толщины слоя

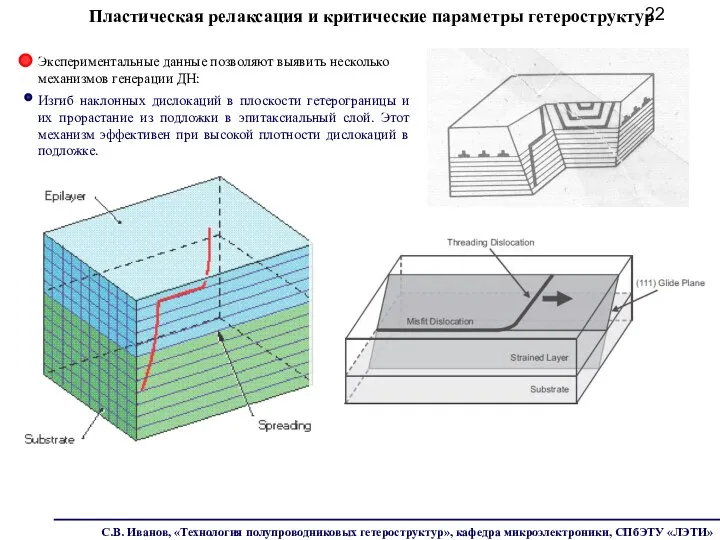
Экспериментальные данные позволяют выявить несколько механизмов генерации ДН:
Пластическая релаксация и критические параметры гетероструктур
Изгиб наклонных дислокаций в плоскости гетерограницы и их прорастание из подложки в эпитаксиальный слой. Этот механизм эффективен при высокой плотности дислокаций в подложке.

Зарождение полупетель наиболее вероятно в процессе осаждения слоя на участках с высокими локальными напряжениями. Такими концентраторами напряжений могут служить края пленки, царапины, микровключения, дефекты упаковки и т.д.
Генерация полупетель может происходить при гетероэпитаксии даже на бездислокационных подложках.
Гетерогенное зарождение полупетель на поверхности роста и их последующее прорастание в плоскость гетерограницы путем скольжения. Скольжение осуществляется последовательным переключением связей.
Пластическая релаксация и критические параметры гетероструктур
ПЭМ изображение с поверхности гетероинтерфейса ZnSe/GaAs, демонстрирующее зарождение ДН на выступе поверхности
ПЭМ изображение с поверхности и в геометрии поперечного сечения, демонстрирующее генерацию ДН в слое ZnSe толщиной 100 нм, выращенного на подложке GaAs (МПЭ)

Пластическая релаксация и критические параметры гетероструктур
Пластическая деформация приводит к уменьшению напряжений. Часть упругой энергии превращается в энергию дислокаций, другая ее доля идет на работу, совершаемую кристаллической решеткой при расширении или сжатии объема твердой фазы после частичной релаксации упругих напряжений. Третья часть упругой энергии остается в кристалле и реализуется через остаточную деформацию.
Энергия деформации решетки на единицу длины дислокации:
G – модуль сдвига, ν - коэффициент Пуассона (отношение относительной поперечной деформации элемента тела к его относительной продольной деформации), ϕ - угол между вектором Бюргерса и осью дислокации, b – вектор Бюргерса, R – кратчайшее расстояние от оси дислокации до свободной поверхности (параметр обрезания) - ограничивает радиус, за которым можно пренебречь влиянием упругого потенциала, rс – размер ядра дислокации
Модель Matthews-Blakeslee
[см., напр., Hirth J., Lothe J., Theory of dislocations, 1982]
Энергия на единицу длины краевой дислокации:
Энергия на единицу длины винтовой дислокации:

Если плоскость гетерограницы ориентирована по грани (100), то =54,74°
Пластическая релаксация и критические параметры гетероструктур
В приближении изотропного кристалла
В первом приближении
угол между плоскостью скольжения и межфазной границей
В AIIIBV устранение дилатационного несоответствия осуществляется за счет образования 60° (ϕ=60°) дислокаций, ориентированных в направлении [110] с вектором Бюргерса
Остаточная упругая деформация уменьшается пропорционально числу дислокаций и проекции краевой компоненты вектора Бюргерса на плоскость границы раздела
Если принять, что дислокации вводятся в границу раздела путем скольжения полупетель с поверхности роста, то для линейной плотности ДН получим:
Для случая, когда релаксация напряжений сопровождается образованием ортогональной сетки, энергия дислокаций на единицу площади:
В частично релаксированном состоянии гетероструктуры часть несоответствия fD
аккомодируется дислокациями и одновременно в эпитаксиальном слое присутствует однородная упругая деформация εr
Стадии нуклеации и роста дислокационных полупетель: кривая (a) представляет докритическую дислокационную полупетлю, (b) представляет полупетлю, которая стабильна под действием напряжений несоответствия, (c) изображает проросшую петлю, с генерацией сегмента LL/ дислокации несоответствия, h - толщина слоя.
множитель «2» учитывает две скрещенные системы из параллельных ДН

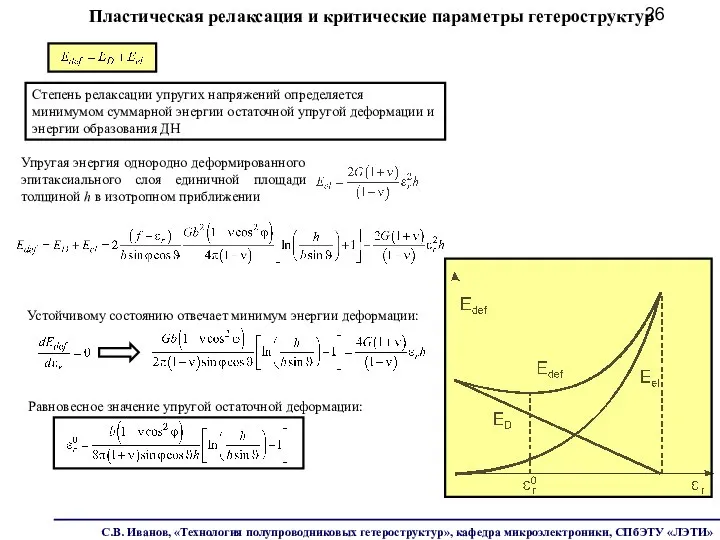
Пластическая релаксация и критические параметры гетероструктур
Устойчивому состоянию отвечает минимум энергии деформации:
Упругая энергия однородно деформированного эпитаксиального слоя единичной площади толщиной h в изотропном приближении
Равновесное значение упругой остаточной деформации:
Степень релаксации упругих напряжений определяется минимумом суммарной энергии остаточной упругой деформации и энергии образования ДН

Пластическая релаксация и критические параметры гетероструктур
Уравнение Мэттьюза-Блэксли. Получено на основе деформационного равновесия гетероструктур. Не содержит модулей сдвига и в этом смысле является универсальным, т. к. применимо для описания любых гетеросистем
(*)
В структуре сфалерита при малых рассогласованиях решеток на гетерогранице энергетически выгодно образование полных 60-градусных (ϕ=60°) дислокаций несоответствия, ориентированных в направлении [110] с вектором Бюргерса
Пример:
Даже в структурах с закритическими толщинами существенная часть несоответствия аккомодируется за счет упругих искажений

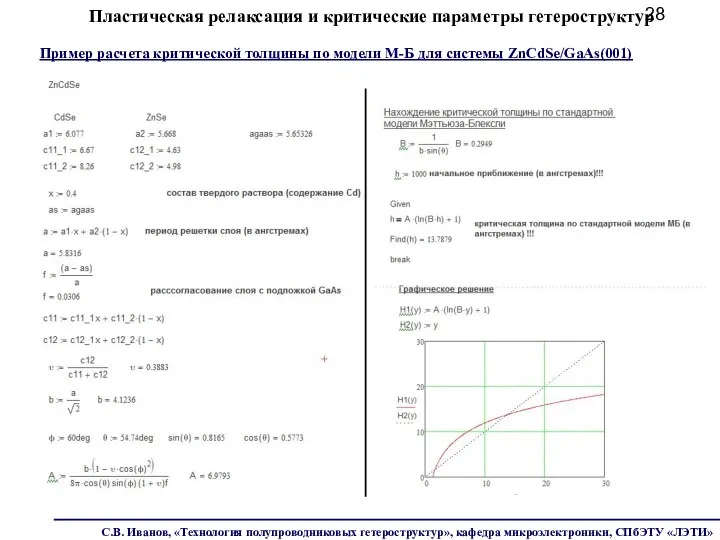
Пластическая релаксация и критические параметры гетероструктур
Пример расчета критической толщины по модели М-Б для системы ZnCdSe/GaAs(001)

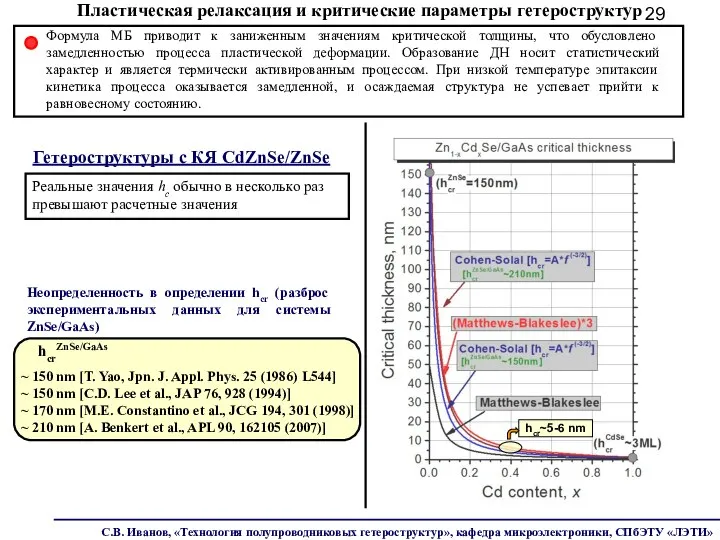
Гетероструктуры с КЯ CdZnSe/ZnSe
Неопределенность в определении hcr (разброс экспериментальных данных для системы ZnSe/GaAs)
hcrZnSe/GaAs
~ 150 nm [T. Yao, Jpn. J. Appl. Phys. 25 (1986) L544]
~ 150 nm [C.D. Lee et al., JAP 76, 928 (1994)]
~ 170 nm [M.E. Constantino et al., JCG 194, 301 (1998)]
~ 210 nm [A. Benkert et al., APL 90, 162105 (2007)]
Реальные значения hc обычно в несколько раз превышают расчетные значения
Формула МБ приводит к заниженным значениям критической толщины, что обусловлено замедленностью процесса пластической деформации. Образование ДН носит статистический характер и является термически активированным процессом. При низкой температуре эпитаксии кинетика процесса оказывается замедленной, и осаждаемая структура не успевает прийти к равновесному состоянию.
Пластическая релаксация и критические параметры гетероструктур

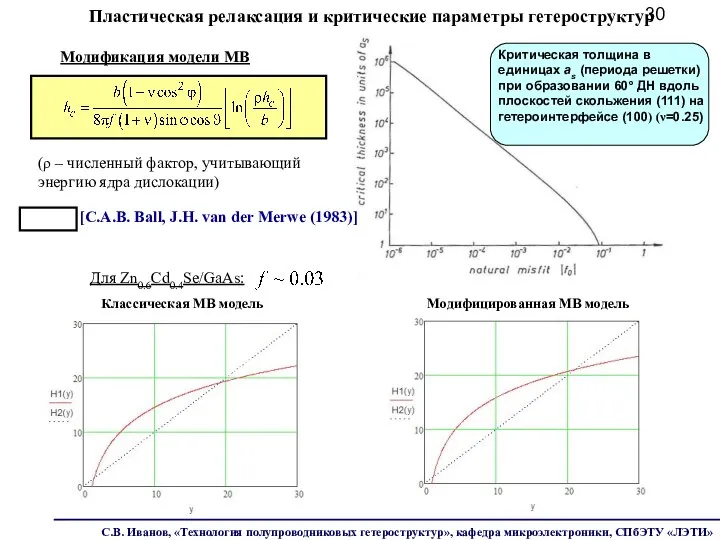
Модификация модели MB
(ρ – численный фактор, учитывающий энергию ядра дислокации)
[C.A.B. Ball, J.H. van der Merwe (1983)]
Пластическая релаксация и критические параметры гетероструктур
Критическая толщина в единицах as (периода решетки) при образовании 60° ДН вдоль плоскостей скольжения (111) на гетероинтерфейсе (100) (ν=0.25)
Модифицированная MB модель
Классическая MB модель
Для Zn0.6Cd0.4Se/GaAs:

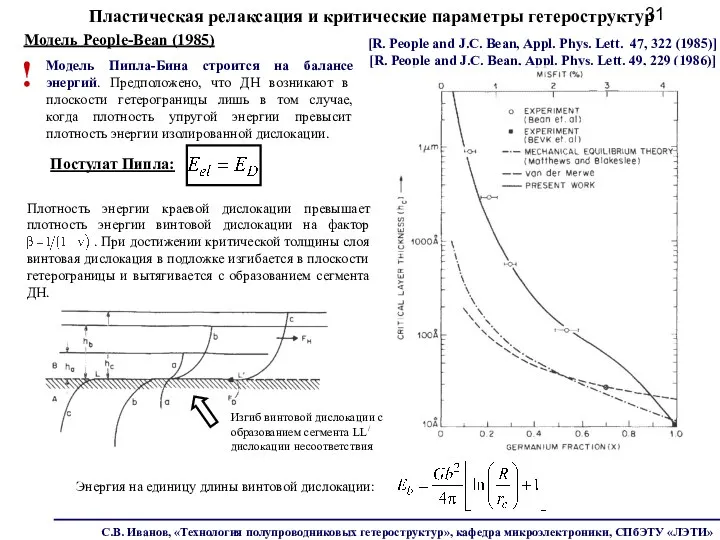
Пластическая релаксация и критические параметры гетероструктур
Модель Пипла-Бина строится на балансе энергий. Предположено, что ДН возникают в плоскости гетерограницы лишь в том случае, когда плотность упругой энергии превысит плотность энергии изолированной дислокации.
Модель People-Bean (1985)
Постулат Пипла:
Энергия на единицу длины винтовой дислокации:
!
Изгиб винтовой дислокации с образованием сегмента LL/ дислокации несоответствия
[R. People and J.C. Bean, Appl. Phys. Lett. 47, 322 (1985)]
[R. People and J.C. Bean, Appl. Phys. Lett. 49, 229 (1986)]

Пластическая релаксация и критические параметры гетероструктур
Поверхностная плотность энергии, связанная с изолированной винтовой дислокацией для слоя толщиной h:
Трудно оценить плотность энергии, связанной с изолированной винтовой дислокацией
Поверхностная плотность упругой энергии:
Формула Пипла
Пример:
Значения hc сильно возрастают по сравнению с МБ. Модель МБ более обоснована, но на практике деформационное равновесие не реализуется, т.к. образование дислокаций – термически активированный процесс и может характеризоваться замедленной кинетикой. Замедленность процессов зарождения и перемещения ДН в условиях достаточно высокой скорости осаждения слоев приводит к «замораживанию» упруго-напряженного состояния гетероструктуры. Реально распределение дислокаций почти всегда оказывается неравновесным.
Важно обеспечить согласование периодов решеток при температуре эпитаксии (пластическая деформация маловероятна при охлаждении гетероструктуры, так как экспоненциально возрастает предел текучести). При охлаждении изопериодной гетероструктуры – термоупругие напряжения (как правило, не релаксируют).
w – протяженность области деформации вдоль плоскости скольжения для изолированной дислокации.
В модели Пипла-Бина для соответствия эксперименту в систему Si1-xGex/Si - w=5b.
для системы Si1-xGex/Si

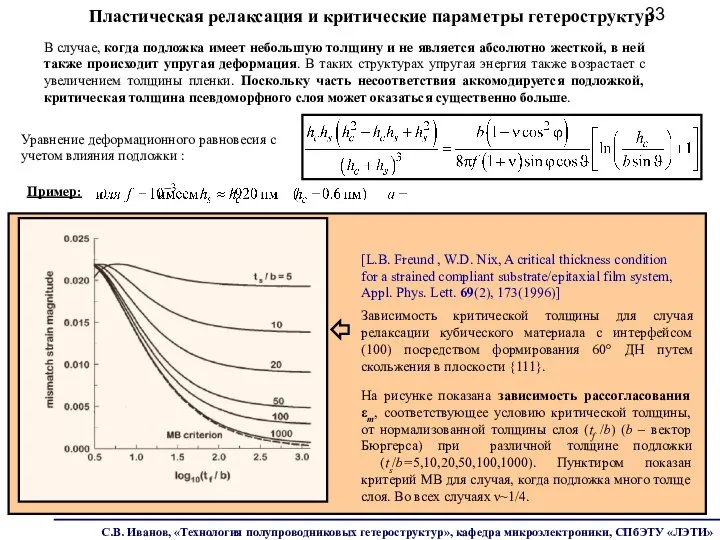
Пластическая релаксация и критические параметры гетероструктур
[L.B. Freund , W.D. Nix, A critical thickness condition for a strained compliant substrate/epitaxial film system, Appl. Phys. Lett. 69(2), 173(1996)]
На рисунке показана зависимость рассогласования εm, соответствующее условию критической толщины, от нормализованной толщины слоя (tf /b) (b – вектор Бюргерса) при различной толщине подложки
(ts/b=5,10,20,50,100,1000). Пунктиром показан критерий MB для случая, когда подложка много толще слоя. Во всех случаях ν~1/4.
Уравнение деформационного равновесия с учетом влияния подложки :
В случае, когда подложка имеет небольшую толщину и не является абсолютно жесткой, в ней также происходит упругая деформация. В таких структурах упругая энергия также возрастает с увеличением толщины пленки. Поскольку часть несоответствия аккомодируется подложкой, критическая толщина псевдоморфного слоя может оказаться существенно больше.
Пример:
Зависимость критической толщины для случая релаксации кубического материала с интерфейсом (100) посредством формирования 60° ДН путем скольжения в плоскости {111}.

Пластическая релаксация и критические параметры гетероструктур
[Jan H. van dar Merwe and W. A. Jesser, Appl. Phys. Lett. 63 (5), 1509 (1988)]
Рассмотрен случай эпитаксиальных сверхрешеток со слоями равной толщины и одинаковыми упругими свойствами. Проведено сравнение энергии ДН в СР по сравнению с толстым одиночным слоем при малых толщинах слоёв СР и малых f .
Основной вывод:
Показано, что энергия образования ДН уменьшается на ~20% в случае монослойной СР с малым f по сравнению со случаем роста одиночного монослоя на толстой подложке.
Критическая толщина в случае СР в 4-5 раз превышает hc для одиночного слоя
В многослойных гетероструктурах критическую толщину можно оценить по
эквивалентной деформации структуры

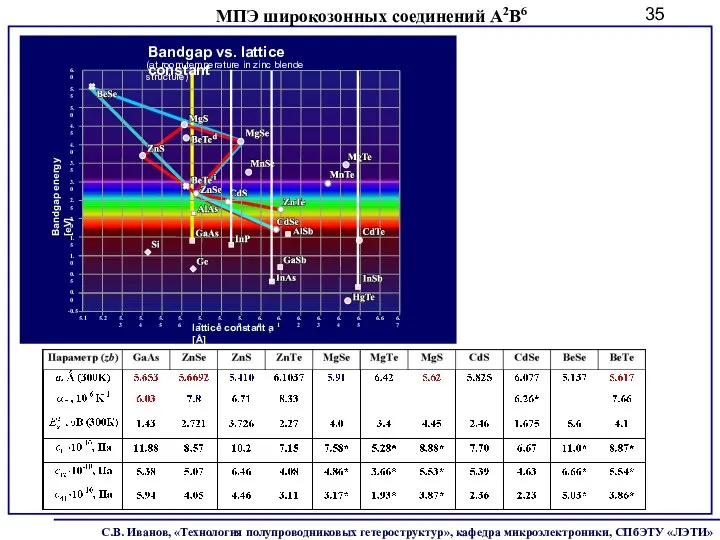
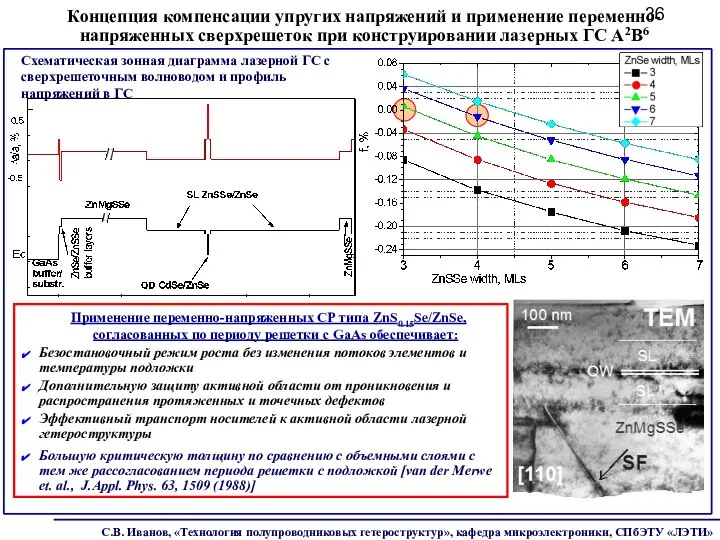
МПЭ широкозонных соединений А2В6

Схематическая зонная диаграмма лазерной ГС с сверхрешеточным волноводом и профиль напряжений в ГС
Концепция компенсации упругих напряжений и применение переменно-напряженных сверхрешеток при конструировании лазерных ГС A2B6
Применение переменно-напряженных СР типа ZnS0.15Se/ZnSe, согласованных по периоду решетки с GaAs обеспечивает:
Безостановочный режим роста без изменения потоков элементов и температуры подложки
Дополнительную защиту активной области от проникновения и распространения протяженных и точечных дефектов
Эффективный транспорт носителей к активной области лазерной гетероструктуры
Большую критическую толщину по сравнению с объемными слоями с тем же рассогласованием периода решетки с подложкой [van der Merwe et. al., J.Appl. Phys. 63, 1509 (1988)]

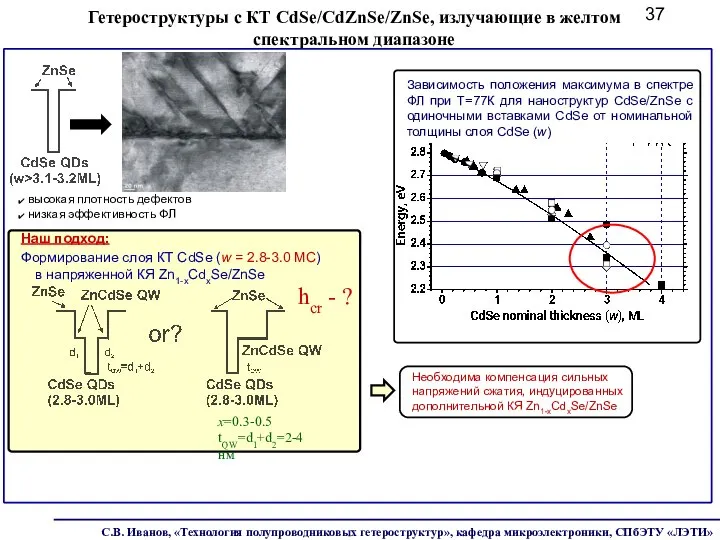
Гетероструктуры с КТ CdSe/CdZnSe/ZnSe, излучающие в желтом спектральном диапазоне
высокая плотность дефектов
низкая эффективность ФЛ
hcr - ?
x=0.3-0.5
tQW=d1+d2=2-4 нм
Необходима компенсация сильных напряжений сжатия, индуцированных дополнительной КЯ Zn1-xCdxSe/ZnSe
Зависимость положения максимума в спектре ФЛ при T=77К для наноструктур CdSe/ZnSe с одиночными вставками CdSe от номинальной толщины слоя CdSe (w)
Наш подход:
Формирование слоя КТ CdSe (w = 2.8-3.0 МС)
в напряженной КЯ Zn1-xCdxSe/ZnSe

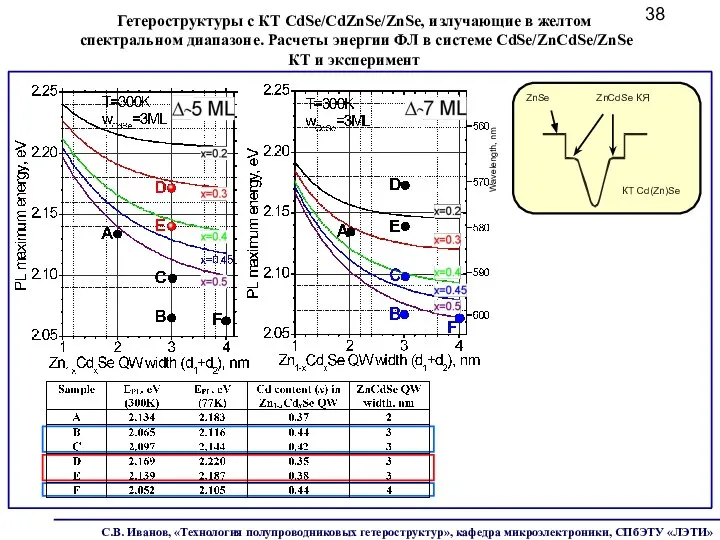
Wavelength, nm
КТ Cd(Zn)Se
ZnSe
ZnCdSe КЯ
Гетероструктуры с КТ CdSe/CdZnSe/ZnSe, излучающие в желтом спектральном диапазоне. Расчеты энергии ФЛ в системе CdSe/ZnCdSe/ZnSe КТ и эксперимент

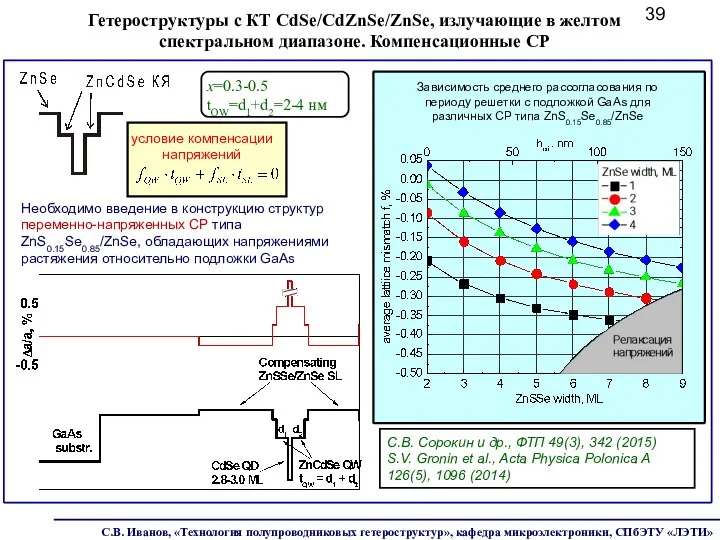
Зависимость среднего рассогласования по периоду решетки с подложкой GaAs для различных СР типа ZnS0.15Se0.85/ZnSe
С.В. Сорокин и др., ФТП 49(3), 342 (2015)
S.V. Gronin et al., Acta Physica Polonica A 126(5), 1096 (2014)
x=0.3-0.5
tQW=d1+d2=2-4 нм
Гетероструктуры с КТ CdSe/CdZnSe/ZnSe, излучающие в желтом спектральном диапазоне. Компенсационные СР
Необходимо введение в конструкцию структур переменно-напряженных СР типа ZnS0.15Se0.85/ZnSe, обладающих напряжениями растяжения относительно подложки GaAs
условие компенсации
напряжений

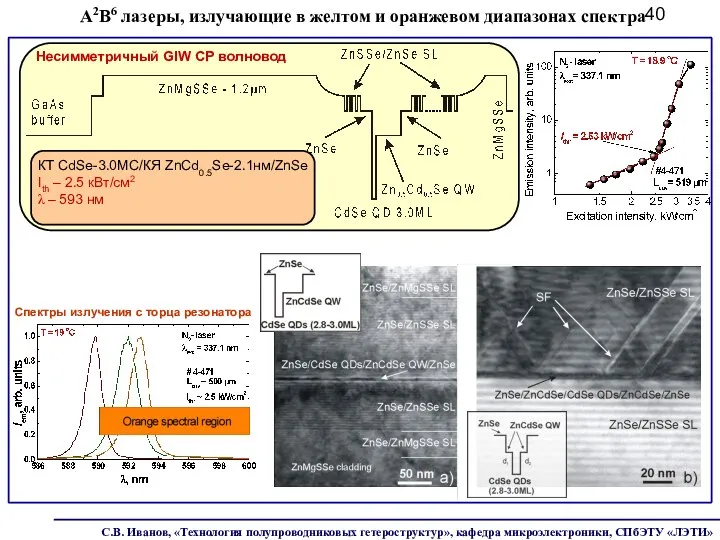
КТ CdSe-3.0МС/КЯ ZnCd0.5Se-2.1нм/ZnSe
Ith – 2.5 кВт/см2
λ – 593 нм
Несимметричный GIW СР волновод
Спектры излучения с торца резонатора
А2В6 лазеры, излучающие в желтом и оранжевом диапазонах спектра

Пластическая релаксация в градиентных слоях
(на примере системы InxGa1-xAs)
Изображение, полученное методом просвечивающей электронной микроскопии в геометрии поперечного сечения, структуры с 1μm-InxGa1-xAs метаморфным буферным слоем с линейным профилем изменения состава
В слоях с линейным градиентом состава не происходит полной релаксации упругих напряжений. Остаточная деформация в этих структурах приводит к образованию вблизи поверхности МБС напряженной области, свободной от дислокаций (или, корректнее, области с низкой плотностью ПД), в то время как в остальной части метаморфного буфера наблюдается практически полная релаксация напряжений посредством образования ДН
Применение концепции метаморфного роста позволяет значительно улучшить характеристики гетероструктур, выращиваемых на рассогласованных подложках, а также расширить функциональные возможности полупроводниковых приборов, выращиваемых на подложках GaAs методом молекулярно-пучковой эпитаксии.
Дислокационная структура может формироваться и в градиентных слоях. Градиент состава и обусловленный им градиент рассогласования решеток не снижает общего числа ДН, однако способствует их более равномерному распределению в структуре. Сетка ДН имеет многоэтажный характер.
Стандартный подход заключается в выращивании буферного слоя материала с требуемой постоянной решетки и при этом достаточной толщины, для того чтобы снять напряжения несоответствия посредством образования дислокаций и их «захоронения» в глубине структуры ниже слоя совершенного материала.

Пластическая релаксация в градиентных слоях
(на примере системы InxGa1-xAs)
In situ измерения аккомодированных напряжений при МПЭ InxGa1−xAs (x=0.2) толщиной 450 нм, скорость роста 0.5 МС/с. Прямая линия показывает зону псевдоморфного роста.
[M. U. González et al., Appl. Phys. Lett. 81, 4162 (2002).
ПЭМ изображение в геометрии поперечного сечения структуры
с 1μm-In0.3Ga0.7As слоем, выращенном на поверхности МБС
Остаточная деформация в МБС слоях должна быть учтена при последующем росте структуры. Эта задача решается посредством согласования периода решетки последующей структуры с латеральным периодом решетки буферного слоя. Другими словами, необходимо уменьшить состав верхнего слоя на такую величину (так называемая обратная ступень (Δx) – step-back), чтобы латеральный период решетки у поверхности напряженного градиентного слоя был равен равновесному (ненапряженному) периоду решетки верхнего слоя

Согласно модели Данстана [Appl. Phys. Lett. 72, 1875 (1998) ]
для слоев с линейным градиентом состава деформация вблизи поверхности ГБС
не зависит от толщины градиентного слоя или от достигнутого максимального состава, а толщина напряженной свободной от дислокаций области равна
Для того, чтобы в верхнем слое структуры с метаморфным буфером с линейным градиентом состава отсутствовали напряжения
Пластическая релаксация в градиентных слоях
(на примере системы InxGa1-xAs)
- скорость изменения состава градиентного слоя, выраженная в виде эквивалентного напряжения/единицу длины
- константа релаксации, которая для системы InxGa1-xAs/GaAs составляет
[J. Tersoff, Dislocations and strain relief in compositionally graded layers, Applied Physics Letters 62, 693-5 (1993)]
[D. J. Dunstan, Strain and strain relaxation in semiconductors, J. Mater. Sci.: Mater. Electron. 8, 337–75 (1997)]
[F. Romanato, E. Napolitani, A. Carnera, A.V. Drigo, L. Lazzarini, G. Salviati, C. Ferrari, A. Bosacchi, and S. Franchi, Strain relaxation in graded composition InxGa1−xAs/GaAs buffer layers, J. Appl. Phys. 86, 4748-55 (1999)]
При скорости изменения состава 30% In/μm в МБС
InxGa1-xAs/GaAs
[Sorokin et al., JCG (2016)]

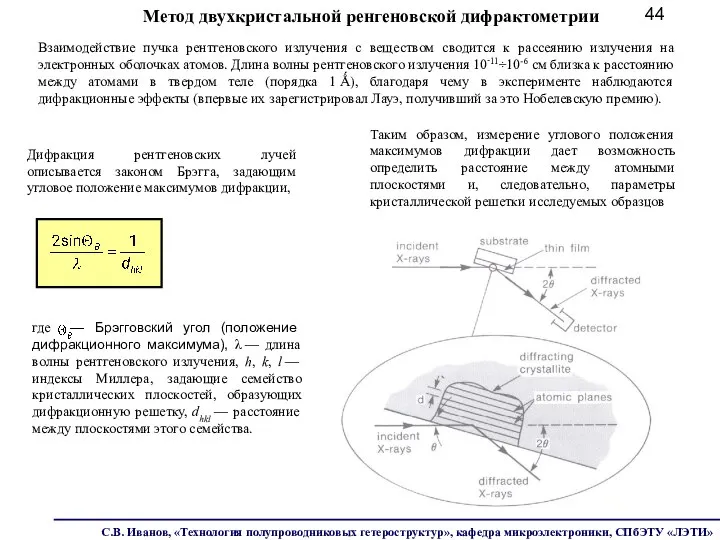
Взаимодействие пучка рентгеновского излучения с веществом сводится к рассеянию излучения на электронных оболочках атомов. Длина волны рентгеновского излучения 10‑11÷10-6 см близка к расстоянию между атомами в твердом теле (порядка 1 Ǻ), благодаря чему в эксперименте наблюдаются дифракционные эффекты (впервые их зарегистрировал Лауэ, получивший за это Нобелевскую премию).
Дифракция рентгеновских лучей описывается законом Брэгга, задающим угловое положение максимумов дифракции,
Метод двухкристальной ренгеновской дифрактометрии
Таким образом, измерение углового положения максимумов дифракции дает возможность определить расстояние между атомными плоскостями и, следовательно, параметры кристаллической решетки исследуемых образцов

Метод двухкристальной ренгеновской дифрактометрии
1
2,3
4
5
6
Схема дифракционного эксперимента:
1 — трубка, 2 — окно, 3 — монохроматор, 4 — образец, 5 — поворотный столик, 6 — детектор

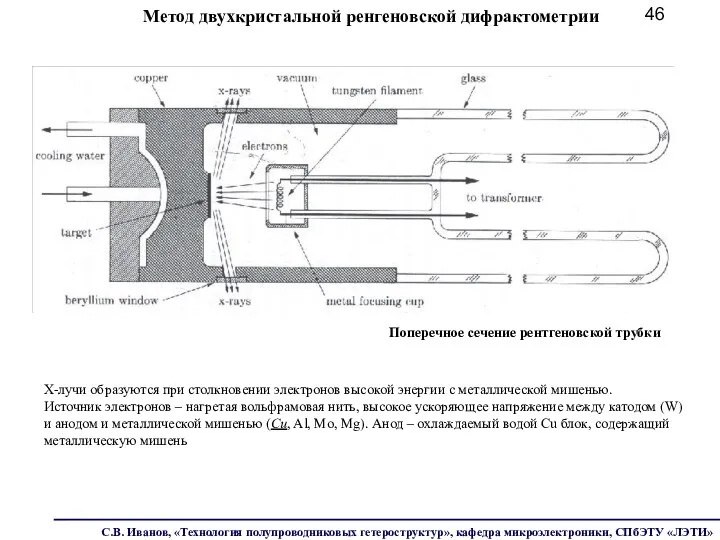
Метод двухкристальной ренгеновской дифрактометрии
Поперечное сечение рентгеновской трубки
X-лучи образуются при столкновении электронов высокой энергии с металлической мишенью.
Источник электронов – нагретая вольфрамовая нить, высокое ускоряющее напряжение между катодом (W) и анодом и металлической мишенью (Cu, Al, Mo, Mg). Анод – охлаждаемый водой Cu блок, содержащий металлическую мишень

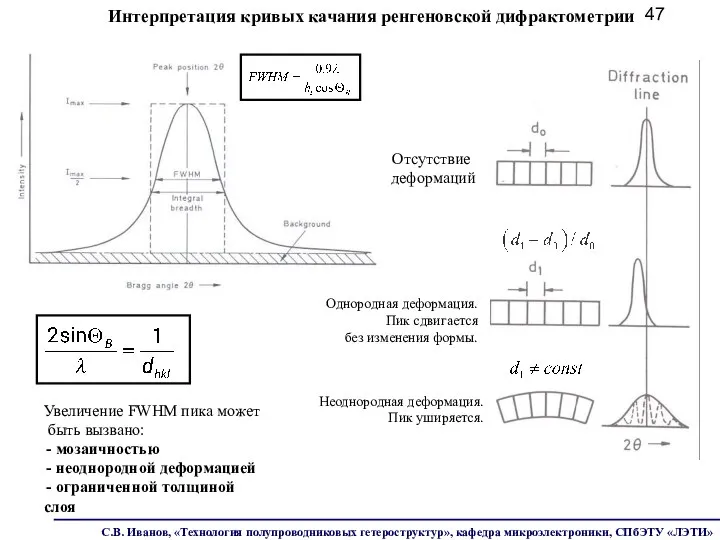
Однородная деформация.
Пик сдвигается
без изменения формы.
Неоднородная деформация.
Пик уширяется.
Интерпретация кривых качания ренгеновской дифрактометрии
Отсутствие деформаций
Увеличение FWHM пика может
быть вызвано:
мозаичностью
неоднородной деформацией
ограниченной толщиной слоя

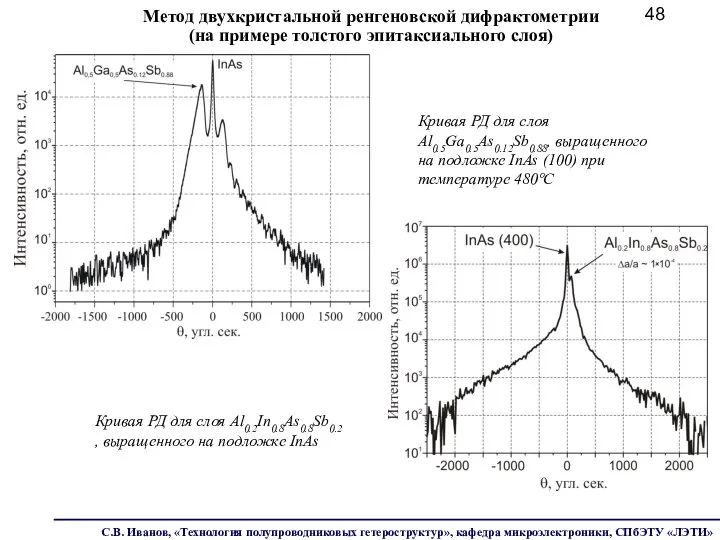
Кривая РД для слоя Al0.5Ga0.5As0.12Sb0.88, выращенного на подложке InAs (100) при температуре 480ºС
Кривая РД для слоя Al0.2In0.8As0.8Sb0.2 , выращенного на подложке InAs
Метод двухкристальной ренгеновской дифрактометрии
(на примере толстого эпитаксиального слоя)

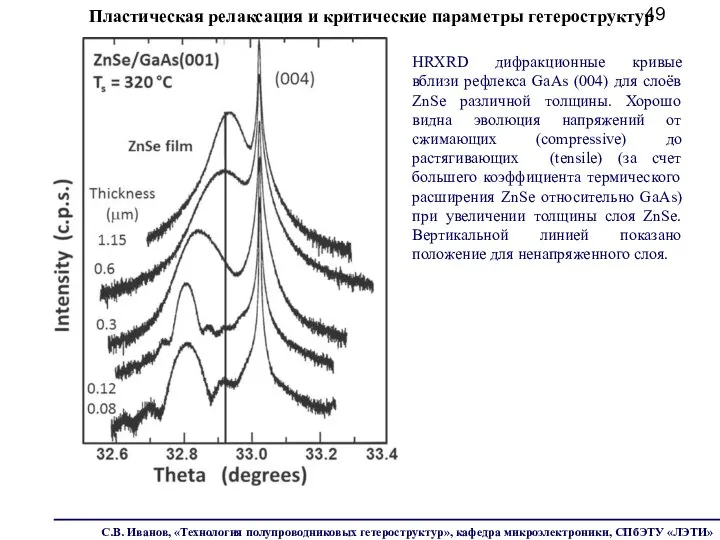
HRXRD дифракционные кривые вблизи рефлекса GaAs (004) для слоёв ZnSe различной толщины. Хорошо видна эволюция напряжений от сжимающих (compressive) до растягивающих (tensile) (за счет большего коэффициента термического расширения ZnSe относительно GaAs) при увеличении толщины слоя ZnSe. Вертикальной линией показано положение для ненапряженного слоя.
Пластическая релаксация и критические параметры гетероструктур

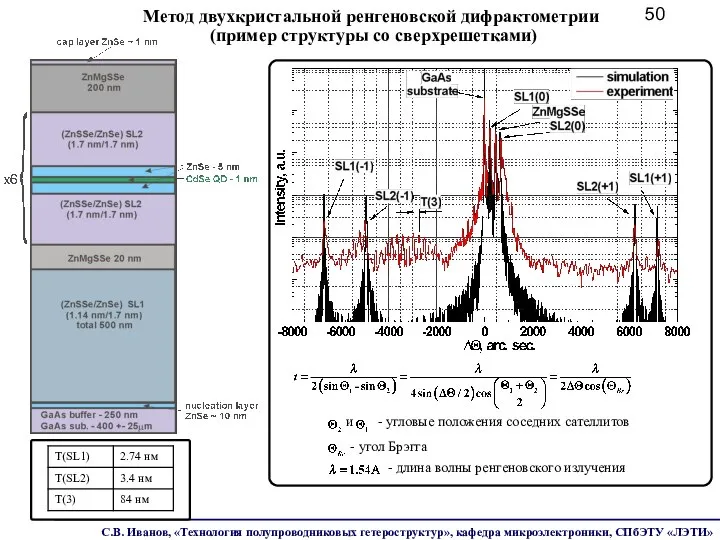
и - угловые положения соседних сателлитов
- угол Брэгга
- длина волны ренгеновского излучения
Метод двухкристальной ренгеновской дифрактометрии
(пример структуры со сверхрешетками)

Метод поляризации фотолюминесценции
Плосконапряженное состояние эпитаксиального слоя эквивалентно одноосной деформации, которая вызывает снятие вырождения валентной зоны в точке k=0. Это проявляется в разделении подзон легких и тяжелых дырок. При сжатии эпитаксиального слоя вдоль направления роста ближе ко дну зоны проводимости находится подзона легких дырок, а при растяжении подзона тяжелых дырок. При люминесценции реализуются переходы в обе подзоны. Различная поляризация позволяет экспериментально определить энергетический сдвиг между подзонами легких и тяжелых дырок Δ.
Несоответствие периодов решеток связано с
расщеплением подзон простыми соотношениями:
b и d –экспериментально определяемые сдвиговые константы деформационного потенциала
Δ – порядка единиц мэВ

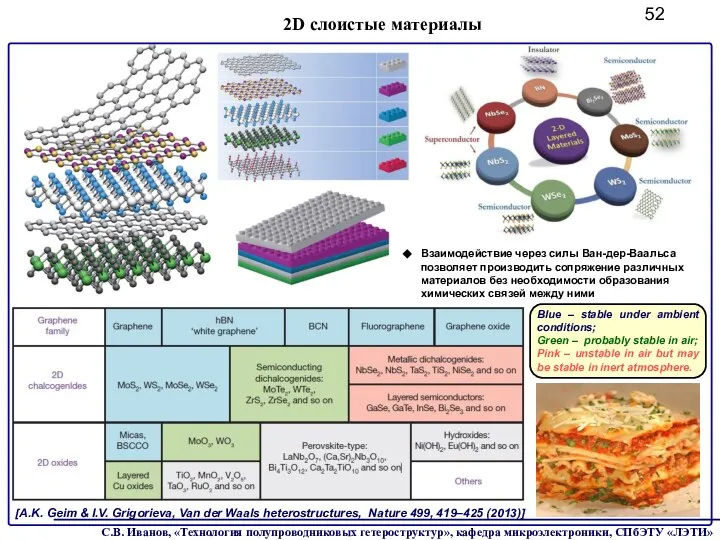
2D слоистые материалы
[A.K. Geim & I.V. Grigorieva, Van der Waals heterostructures, Nature 499, 419–425 (2013)]
Взаимодействие через силы Ван-дер-Ваальса позволяет производить сопряжение различных материалов без необходимости образования химических связей между ними
Blue ‒ stable under ambient conditions;
Green ‒ probably stable in air;
Pink ‒ unstable in air but may be stable in inert atmosphere.

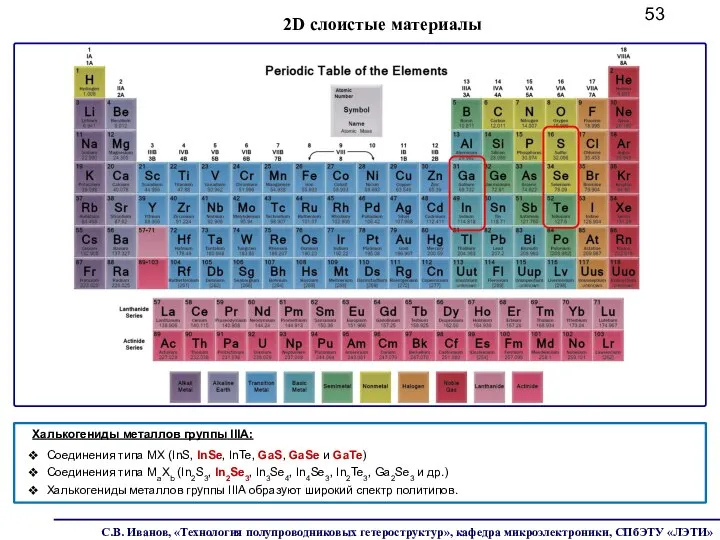
Халькогениды металлов группы IIIA:
Соединения типа MX (InS, InSe, InTe, GaS, GaSe и GaTe)
Соединения типа MaXb (In2S3, In2Se3, In3Se4, In4Se3, In2Te3, Ga2Se3 и др.)
Халькогениды металлов группы IIIA образуют широкий спектр политипов.
2D слоистые материалы

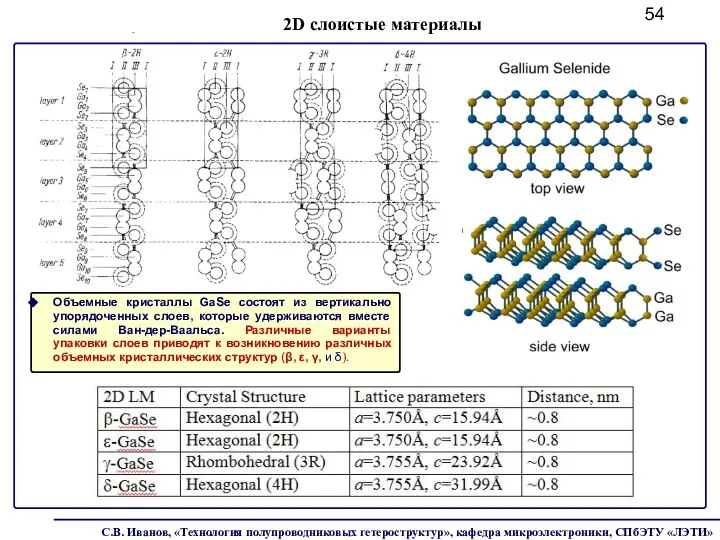
Объемные кристаллы GaSe состоят из вертикально упорядоченных слоев, которые удерживаются вместе силами Ван-дер-Ваальса. Различные варианты упаковки слоев приводят к возникновению различных объемных кристаллических структур (β, ε, γ, и δ).
2D слоистые материалы

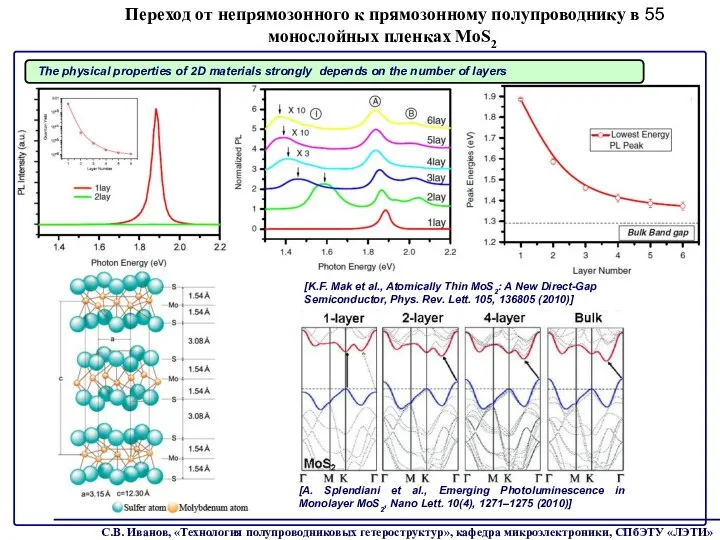
Переход от непрямозонного к прямозонному полупроводнику в монослойных пленках MoS2
[K.F. Mak et al., Atomically Thin MoS2: A New Direct-Gap Semiconductor, Phys. Rev. Lett. 105, 136805 (2010)]
[A. Splendiani et al., Emerging Photoluminescence in Monolayer MoS2, Nano Lett. 10(4), 1271–1275 (2010)]
The physical properties of 2D materials strongly depends on the number of layers

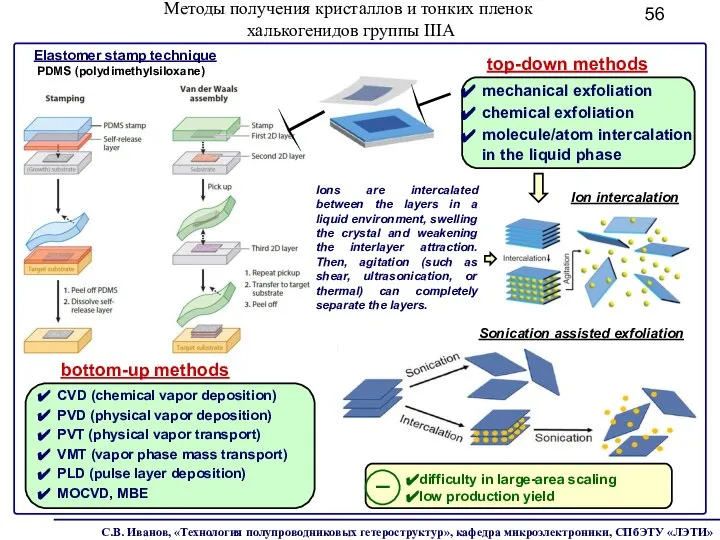
Методы получения кристаллов и тонких пленок
халькогенидов группы IIIA
Ion intercalation
top-down methods
Sonication assisted exfoliation
Elastomer stamp technique
bottom-up methods
mechanical exfoliation
chemical exfoliation
molecule/atom intercalation
in the liquid phase
CVD (chemical vapor deposition)
PVD (physical vapor deposition)
PVT (physical vapor transport)
VMT (vapor phase mass transport)
PLD (pulse layer deposition)
MOCVD, MBE
PDMS (polydimethylsiloxane)
Ions are intercalated between the layers in a liquid environment, swelling the crystal and weakening the interlayer attraction. Then, agitation (such as shear, ultrasonication, or thermal) can completely separate the layers.

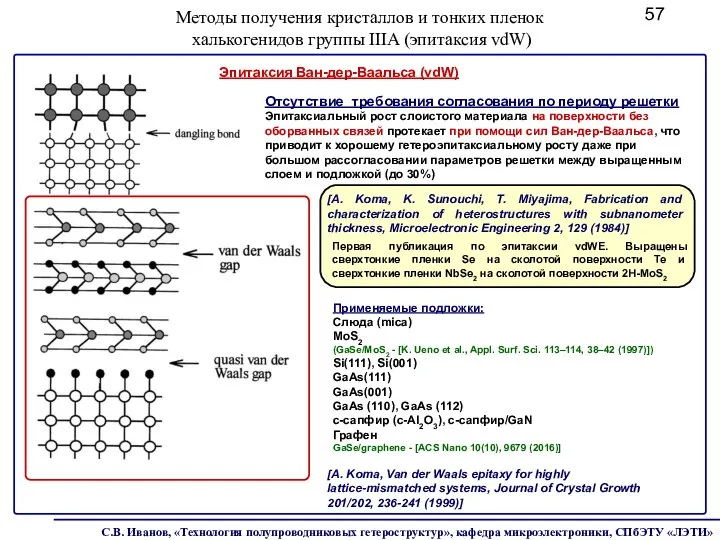
Методы получения кристаллов и тонких пленок
халькогенидов группы IIIA (эпитаксия vdW)
Эпитаксия Ван-дер-Ваальса (vdW)
Отсутствие требования согласования по периоду решетки
Эпитаксиальный рост слоистого материала на поверхности без оборванных связей протекает при помощи сил Ван-дер-Ваальса, что приводит к хорошему гетероэпитаксиальному росту даже при большом рассогласовании параметров решетки между выращенным слоем и подложкой (до 30%)
[A. Koma, K. Sunouchi, T. Miyajima, Fabrication and characterization of heterostructures with subnanometer thickness, Microelectronic Engineering 2, 129 (1984)]
Первая публикация по эпитаксии vdWE. Выращены сверхтонкие пленки Se на сколотой поверхности Te и сверхтонкие пленки NbSe2 на сколотой поверхности 2H-MoS2
Применяемые подложки:
Слюда (mica)
MoS2
(GaSe/MoS2 - [K. Ueno et al., Appl. Surf. Sci. 113–114, 38–42 (1997)])
Si(111), Si(001)
GaAs(111)
GaAs(001)
GaAs (110), GaAs (112)
c-сапфир (с-Al2O3), c-сапфир/GaN
Графен
GaSe/graphene - [ACS Nano 10(10), 9679 (2016)]
[A. Koma, Van der Waals epitaxy for highly lattice-mismatched systems, Journal of Crystal Growth 201/202, 236-241 (1999)]

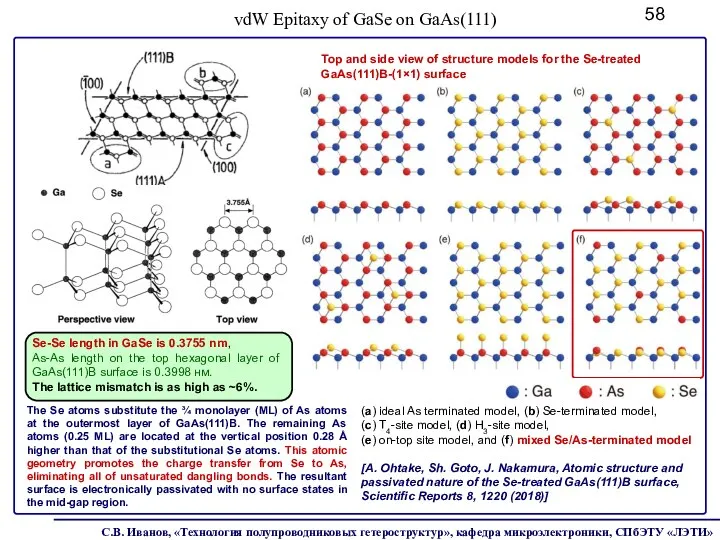
(a) ideal As terminated model, (b) Se-terminated model,
(c) T4-site model, (d) H3-site model,
(e) on-top site model, and (f) mixed Se/As-terminated model
[A. Ohtake, Sh. Goto, J. Nakamura, Atomic structure and passivated nature of the Se-treated GaAs(111)B surface, Scientific Reports 8, 1220 (2018)]
The Se atoms substitute the ¾ monolayer (ML) of As atoms at the outermost layer of GaAs(111)B. The remaining As atoms (0.25 ML) are located at the vertical position 0.28 Å higher than that of the substitutional Se atoms. This atomic geometry promotes the charge transfer from Se to As, eliminating all of unsaturated dangling bonds. The resultant surface is electronically passivated with no surface states in the mid-gap region.
Se-Se length in GaSe is 0.3755 nm,
As-As length on the top hexagonal layer of GaAs(111)B surface is 0.3998 нм.
The lattice mismatch is as high as ~6%.
vdW Epitaxy of GaSe on GaAs(111)
Top and side view of structure models for the Se-treated GaAs(111)B-(1×1) surface

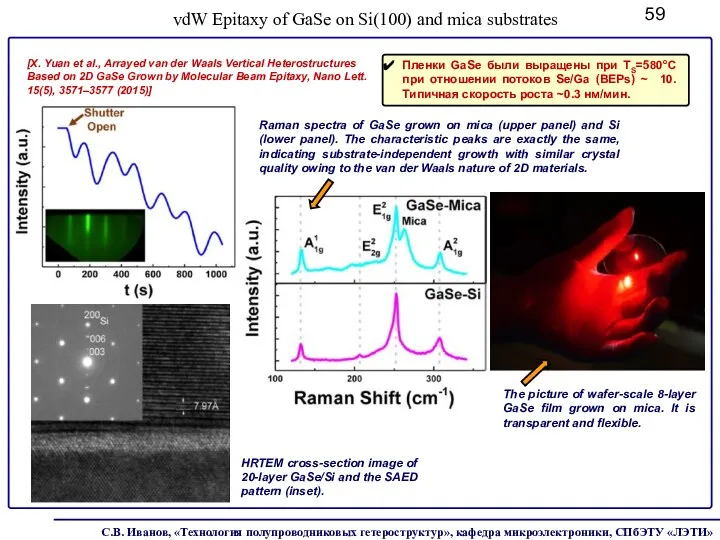
vdW Epitaxy of GaSe on Si(100) and mica substrates
[X. Yuan et al., Arrayed van der Waals Vertical Heterostructures Based on 2D GaSe Grown by Molecular Beam Epitaxy, Nano Lett. 15(5), 3571–3577 (2015)]
Пленки GaSe были выращены при TS=580°C при отношении потоков Se/Ga (BEPs) ~ 10. Типичная скорость роста ~0.3 нм/мин.
HRTEM cross-section image of 20-layer GaSe/Si and the SAED pattern (inset).
Raman spectra of GaSe grown on mica (upper panel) and Si (lower panel). The characteristic peaks are exactly the same, indicating substrate-independent growth with similar crystal quality owing to the van der Waals nature of 2D materials.
The picture of wafer-scale 8-layer GaSe film grown on mica. It is transparent and flexible.