Уравнения

Содержание
1 Понятие уравнения и его свойства
2 Методы решения уравнений
Метод разложения на множители
Метод введения новой переменной
Функционально-графический метод

Теоретическая часть
1 Понятие уравнения (определение, равносильность)
2 Теоремы о равносильности уравнений
3 Понятие алгебраического, рационального, дробно- рационального, иррационального уравнений
4 Суть методов а) разложение на множители
б) замена переменной
в) функционально-графический

Метод разложения на множители
Пример 1. Решить алгебраическое уравнение :
(х-α)³+(х-b)³=(2х-α-b)³ .
Соберём все члены в левой части уравнения и сумму кубов (х-α)³+(х-b)³ разложим на множители. После этого в левой части можно выделить общий множитель 2х-α-b:
(2х-α-b)((х-α)²-(х-α)(х-b)+(х-b)²-(2х-α-b)²)=0,
(2х-α-b)(-3х²+3(α+b)х-3αb)=0.
Отсюда х₁ =(α+b):2, х₂=α, х₃=b.
Ответ:(α+b ):2; α; b.

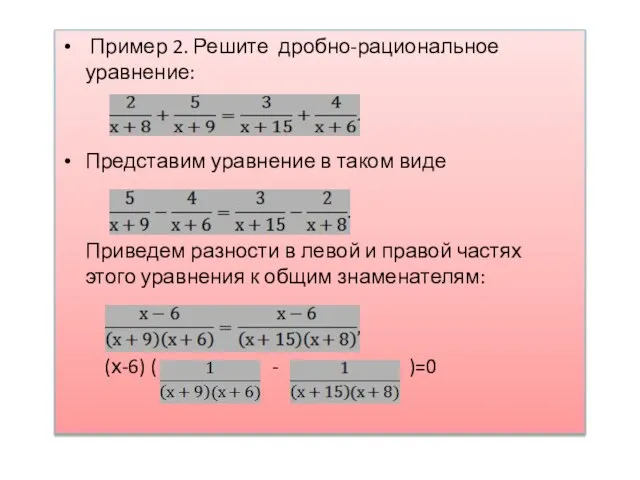
Пример 2. Решите дробно-рациональное уравнение:
Представим уравнение в таком виде
Приведем разности в левой и правой частях этого уравнения к общим знаменателям:
(х-6) ( - )=0

Приравняем нулю каждый из множителей в левой части последнего уравнения. Получим х – 6 =0 или 8х= 66, учитывая при этом, что х=-9, х=-6,
х=-15, х= -8.
Тогда
Ответ: 6,-33/4.

Пример 3.Решите уравнение:
Возведем обе части уравнения в куб, пользуясь формулой (a+b)³=a³+b³+3ab(a+b).
Будем иметь:

А теперь воспользуемся исходным уравнением, на основании которого сумма в скобках равна 1:
Последнее уравнение также возведем в куб:
(х-1)(2х-1)=(1-х)³, (х-1)(2х-1+(х-1)²)=0, (х-1)х²=0.
Отсюда х₁=1, х₂=х₃=0.
Проверка по первоначальному уравнению показывает, что значение х=1 ему удовлетворяет, а значение х=0 – не удовлетворяет.
Ответ: 1.

Введение новой переменной
Пример 4. Решите уравнение:
(х-1)(х-2)(х-4)(х-8)= 4х2.
В левой части уравнения умножим первый множитель на четвёртый, второй на третий, получим: (х²-9х+8)(х²-6х+8)=4х².
А дальше разделим обе части уравнения на х2, пользуясь тем, что значение х=0 не является корнем уравнения:
(x-9+ )(x-6+ )=4

Введем подстановку: х-9+ =у. Будем иметь:
y(у+3)=4, у2+3у-4=0; у1=1, у2=-4.
В обоих случаях найдем х, решая совокупность уравнений
х₁,₂=5
Ответ: 5 .

Пример 5.Решите уравнение: (х+3)⁴+(х+5)⁴=16.
Положим х+4=y ,т. к. =х+4.
Имеем: (y-1)⁴+(y+1)⁴=16. Теперь нужно в левой части уравнения (y-1) и ( y+1) возвести в квадрат, а затем то, что получилось, ещё раз возвести в квадрат. После упрощений образуется биквадратное уравнение: y⁴+6y²-7=0.
Его корни y₁,₂ = . Отсюда х₁=-3, х₂=-5.
Ответ: -3; -5.

Пример 6. Решите уравнение:
Отнимем от обеих частей уравнения
для того, чтобы получить в левой
части квадрат разности:
А теперь очевидная подстановка = у.
Ответ: .

Пример 7. Решите уравнение: х2+8х+8=4(х+2)
Положим =t.
При
это равенство равносильно равенству х+1=t2. Получаем систему рациональных уравнений:
Для ее решения выразим х через t из второго уравнения: х = t2-1.

Подставим это выражение в первое уравнение и новое уравнение упростим
(t2-1)2+8(t2-1)+8=4(t2-1)t,
t4-2t2+1+8t2-8+8=4t3+4t,
t4-4t3+6t2-4t+1=0.
Последнее уравнение имеет корень t=1. Мало того, проверка показывает, что значение t=1 является четырехкратным корнем этого уравнения. Тогда уравнение принимает вид (t-1)4=0. Если t=1, то х=0.
Ответ: 0.

Функционально-графический метод
Пример 8.Решите уравнение:
Найдём область определения D уравнения. Она совпадает с множеством всех решений системы неравенств
Решением первого неравенства является множество
, второго отрезок . Следовательно, область D состоит всего из двух точек -0 и 1. Значение х=0 не удовлетворяет уравнению, значение х=1- удовлетворяет.
Ответ: 1.