В

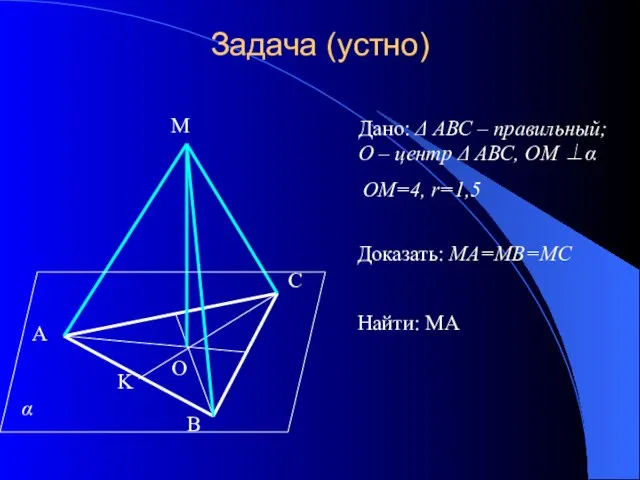
Задача (устно)
А
В
С
О
М
Дано: Δ АВС – правильный;
О – центр Δ АВС, ОМ ⊥α
Доказать: МА=МВ=МС
OM=4, r=1,5
K
Найти: МА
α

Тема урока:
Признак перпендикулярности
прямой и плоскости
(Д/З: П.17, № 128, 131, 133)
Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

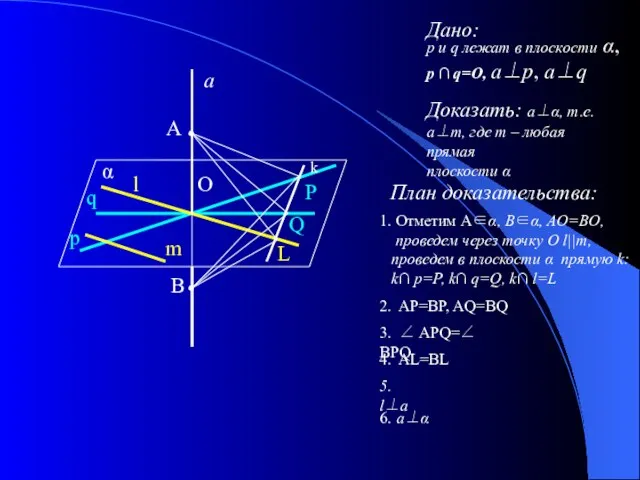
О
А
В
q
p
m
l
α
P
Q
L
Дано:
p и q лежат в плоскости α,
p ∩ q=О, a⊥p, a⊥q
Доказать: a⊥α, т.е.
а⊥m, где m – любая прямая
плоскости α
a
План доказательства:
1. Отметим A∈α, B∈α, AO=BO,
проведем через точку О l||m,
проведем в плоскости α прямую k:
k∩ p=P, k∩ q=Q, k∩ l=L
•
•
2. AP=BP, AQ=BQ
3. ∠ APQ=∠ BPQ
4. AL=BL
5. l⊥a
6. a⊥α
k

Дополнительное задание
Докажите признак перпендикулярности прямой
и плоскости с помощью векторов.
Подсказка используйте следующие факты.
Скалярное произведение взаимно перпендикулярных
векторов равно нулю.
Любой ненулевой вектор можно разложить по двум неколлинеарным векторам.

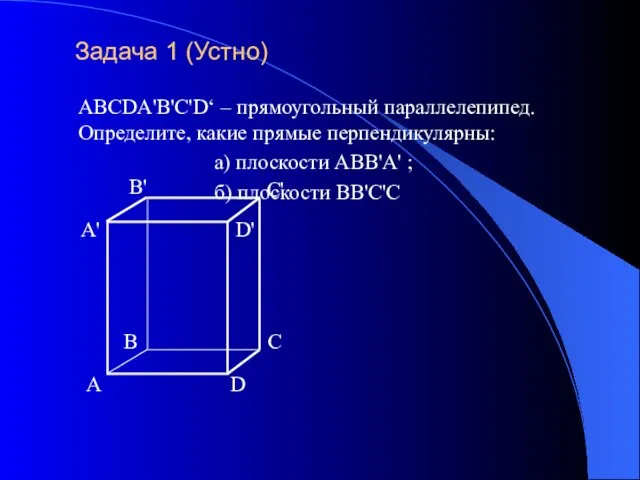
Задача 1 (Устно)
ABCDA'B'C'D‘ – прямоугольный параллелепипед. Определите, какие прямые перпендикулярны:
а) плоскости АВВ'А' ;
б) плоскости ВВ'С'С
А
D
B
C
A'
B'
C'
D'

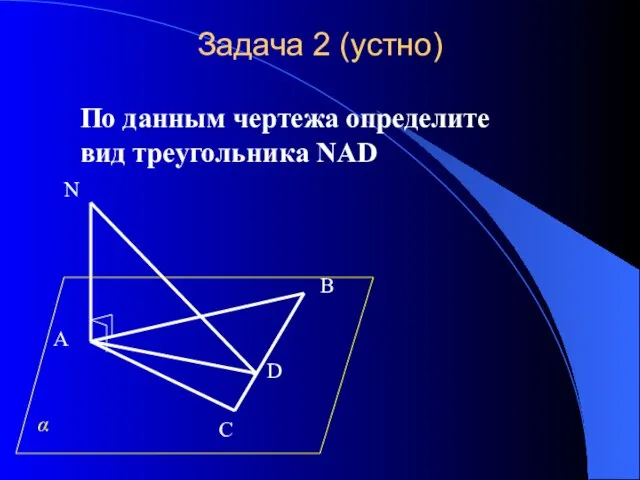
Задача 2 (устно)
По данным чертежа определите
вид треугольника NAD
A
B
C
N
•
D
α

Задача 3 (устно)
Докажите, что если все точки прямой, проведенной через
точку пересечения диагоналей прямоугольника ABCD,
равноудалены от вершин прямоугольника, то прямая
перпендикулярна плоскости прямоугольника.
α
A
B
C
D
O
•
F
f

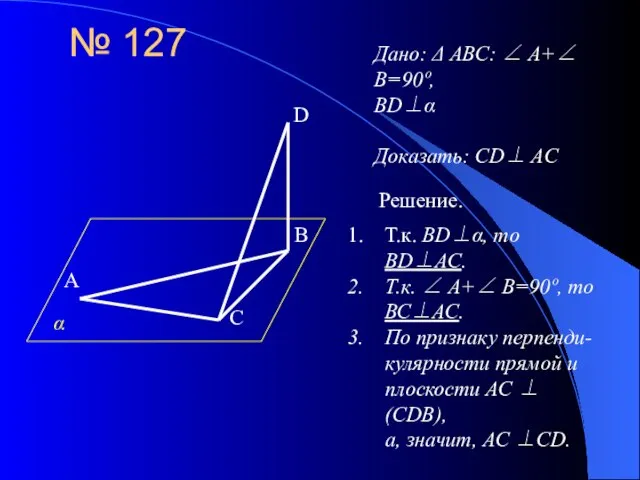
№ 127
Дано: Δ АВС: ∠ А+∠ В=90º,
BD⊥α
Доказать: СD⊥ AC
α
A
B
C
D
Решение.
Т.к. BD⊥α, то BD⊥АС.
Т.к. ∠ А+∠ В=90º, то
ВС⊥АС.
По признаку перпенди-
кулярности прямой и
плоскости АС ⊥(СDB),
а, значит, АС ⊥СD.

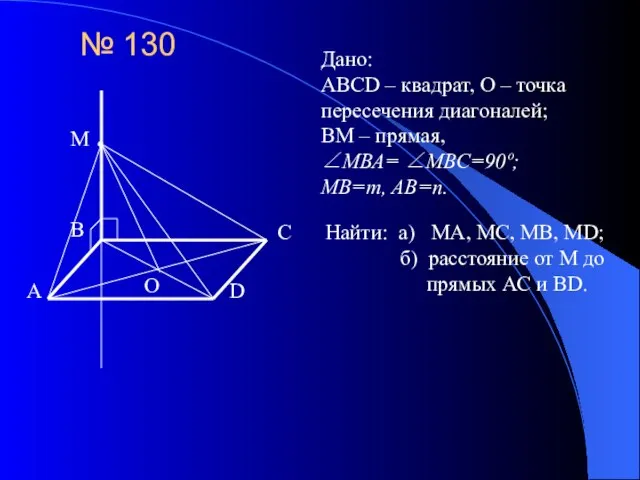
№ 130
Дано:
ABCD – квадрат, О – точка
пересечения диагоналей;
BM – прямая,
∠МВА= ∠МВС=90º;
МВ=m, AB=n.
A
B
C
D
O
•
М
Найти: а) МА, МС, МВ, МD;
б) расстояние от М до
прямых АС и BD.