Вероятностные явления в возмущенных динамических системах

Вероятностные явления связаны с неперестановочностью пределов:
d- неточность знания начальных условий
T- время движения
Возмущенная
система
=
Интегрируемая
система
Возмущение

Темы:
Вероятностное рассеяние при переходах через сепаратрису
Скачки адиабатического инварианта при переходах через сепаратрису
Рассеяние на резонансах, захват в резонанс

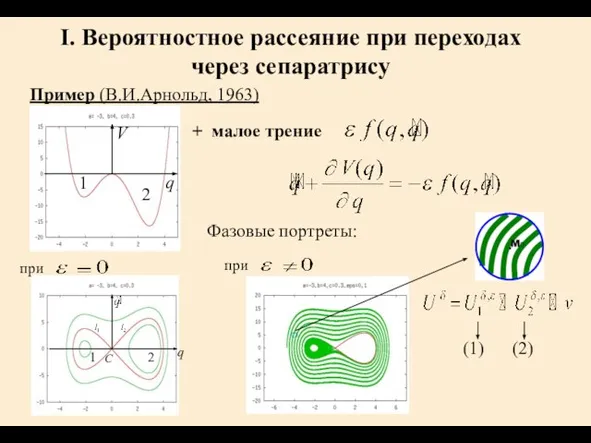
I. Вероятностное рассеяние при переходах через сепаратрису
Пример (В.И.Арнольд, 1963)
V
1
2
q
+ малое трение
Фазовые портреты:
при
при
q
1
2
C
(1)
(2)

Вероятностный подход:
И.М.Лифшиц, А.А.Слуцкин, В.М.Набутовский (1961) - движение заряженных квазичастиц
В.И.Арнольд (1963) - математическое определение вероятности
P.Goldreich, S.Peale (1966) - приливная эволюция вращения планет
А.В.Гуревич, Е.Е.Цидилина (1979) - распространение радиоволн в ионосферных волноводных каналах
G.Wolansky(1990), М.Брин, М.Фрейдлин (1999) - другое определение вероятности (+малая случайная сила) - «ответ» тот же

q
q
Пример: маятник
Фазовый портрет при
Вероятность захвата в колебательный режим (из режима прямого вращения):
, если
, если

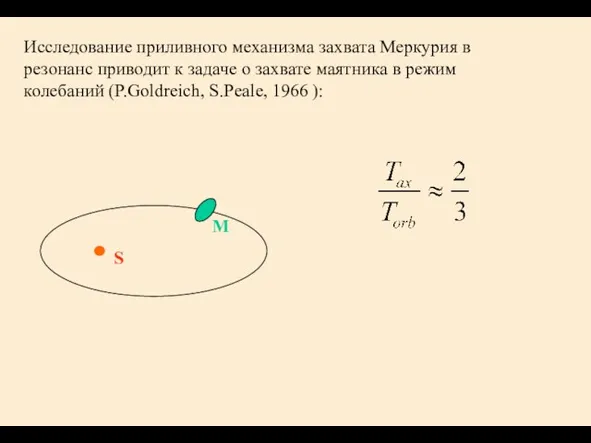
Исследование приливного механизма захвата Меркурия в резонанс приводит к задаче о захвате маятника в режим колебаний (P.Goldreich, S.Peale, 1966 ):
S
M

Общая теория:
Возмущенная
система
=
Система в Rl,
имеющая (l-1) интегралов
Возмущение

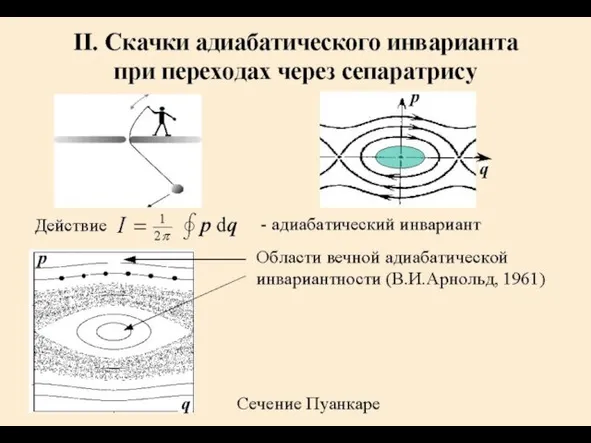
Скачок адиабатического инварианта при переходе маятника через сепаратрису (А.В.Тимофеев, 1978) :
x - квазислучайная величина, распределенная равномерно на (0,1)
Общая формула: А.Н. (1986); J.Cary, D.Escande, J.Tennyson (1986).
Примеры:
Происхождение люка Кирквуда на резонансе 3:1 (J.Wisdom, 1985)
Движение заряженных частиц в хвосте магнитосферы Земли (Й.Бюхнер, Л.М.Зеленый, 1989)

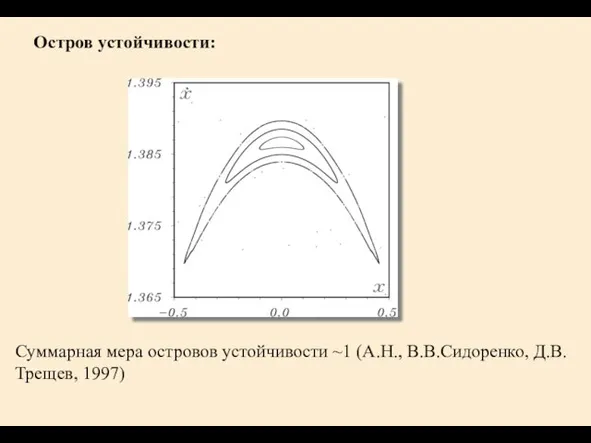
Остров устойчивости:
Суммарная мера островов устойчивости ~1 (А.Н., В.В.Сидоренко, Д.В.Трещев, 1997)

Влияние резонансов
Вблизи резонанса (k, w(I)) = 0 гармоника ei(k,j) не осциллирует.
захват
(k, w(I)) = 0
- резонансная
поверхность
выброс
рассеяние
J(t)
Вероятность захвата ~
Смещение ~
Амплитуда рассеяния ~

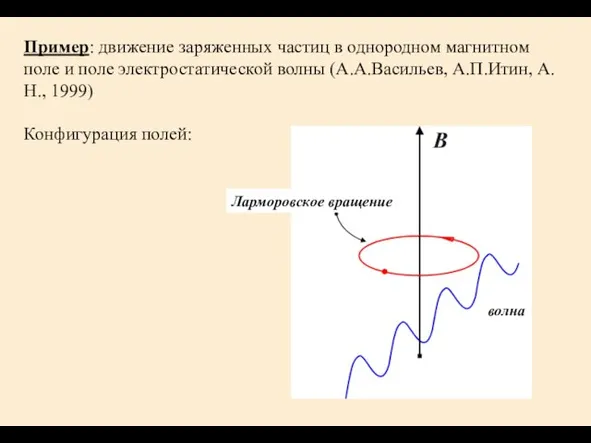
Пример: движение заряженных частиц в однородном магнитном поле и поле электростатической волны (А.А.Васильев, А.П.Итин, А.Н., 1999)
Конфигурация полей:
Ларморовское вращение
волна

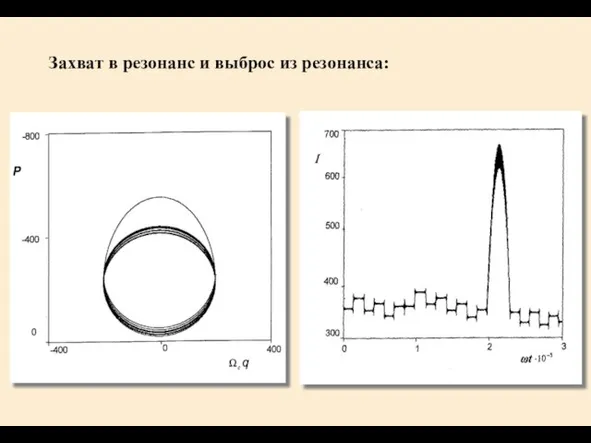
Захват в резонанс и выброс из резонанса:

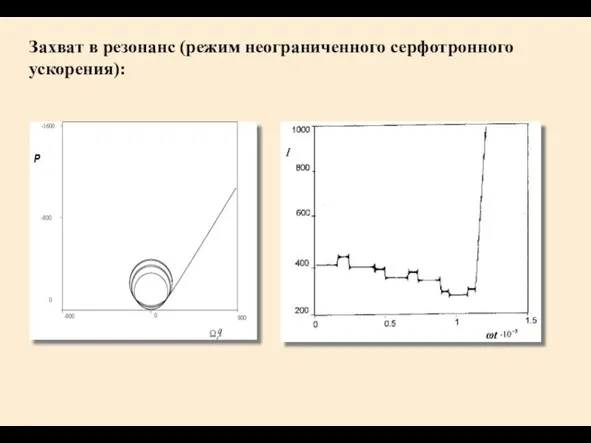
Захват в резонанс (режим неограниченного серфотронного ускорения):

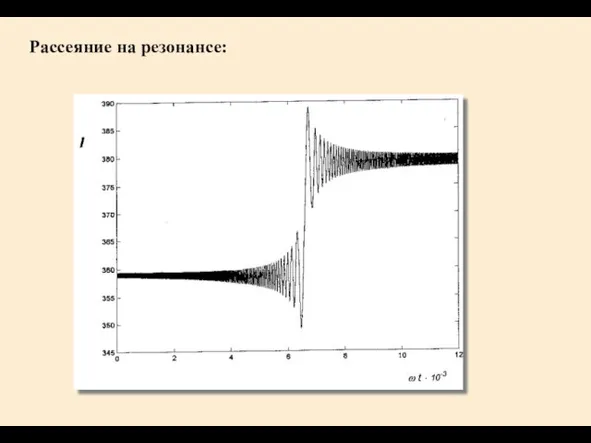
Рассеяние на резонансе:

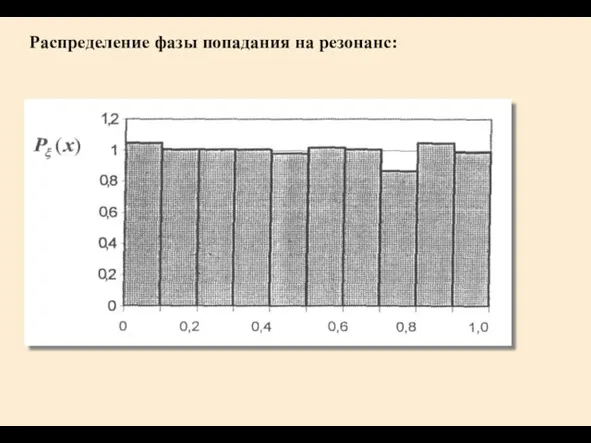
Распределение фазы попадания на резонанс:

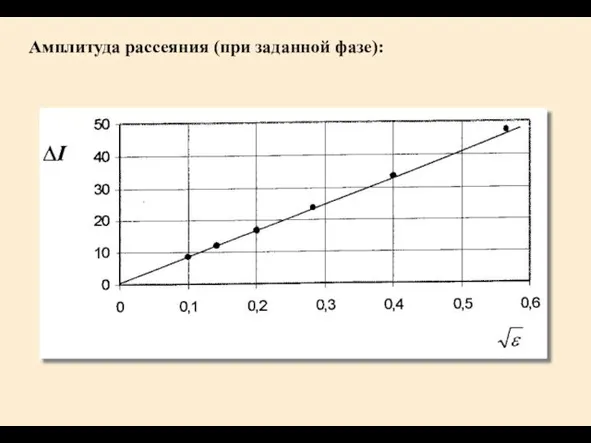
Амплитуда рассеяния (при заданной фазе):