Презентация на тему Резонанс в параллельном колебательном контуре

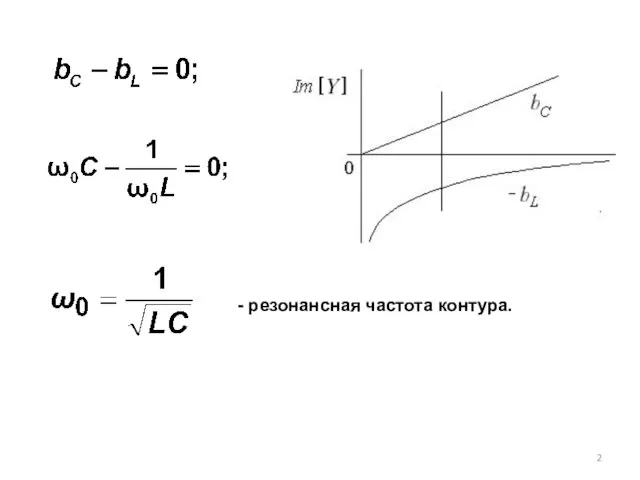
- резонансная частота контура.

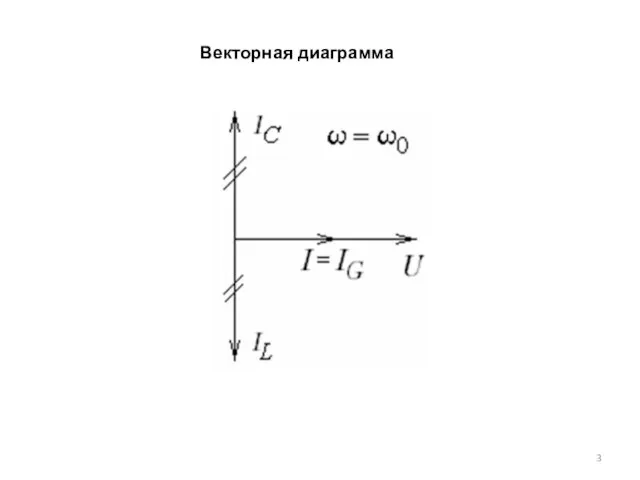
Векторная диаграмма

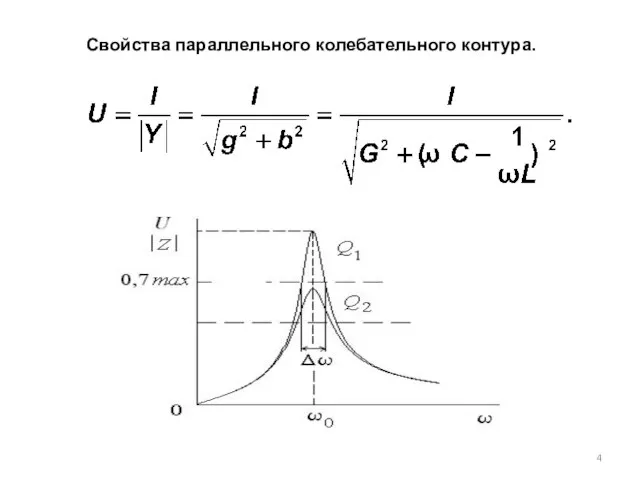
Свойства параллельного колебательного контура.

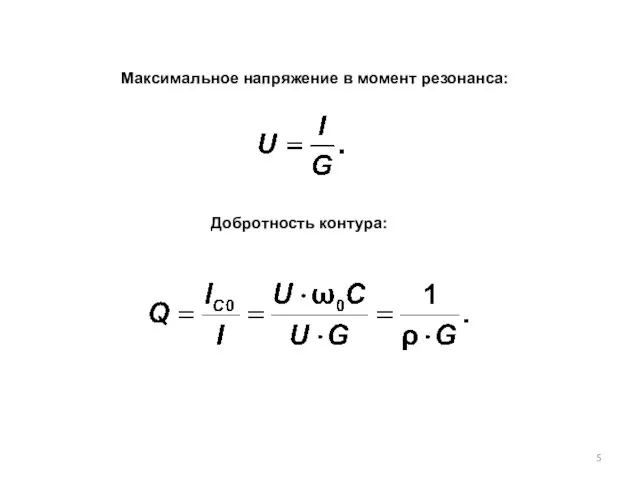
Максимальное напряжение в момент резонанса:
Добротность контура:

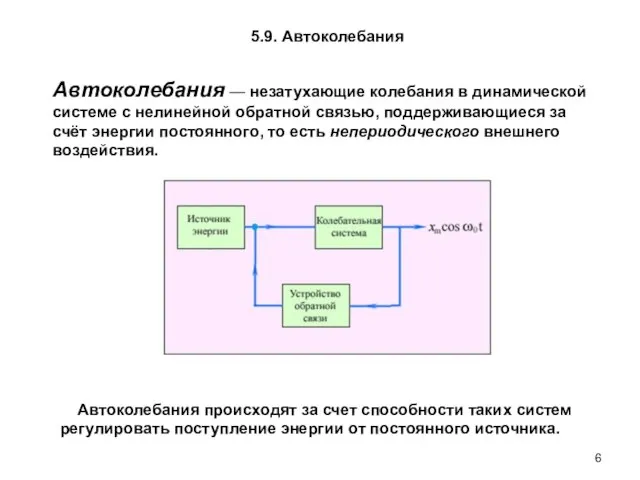
5.9. Автоколебания
Автоколебания происходят за счет способности таких систем регулировать поступление энергии от постоянного источника.
Автоколебания — незатухающие колебания в динамической системе с нелинейной обратной связью, поддерживающиеся за счёт энергии постоянного, то есть непериодического внешнего воздействия.

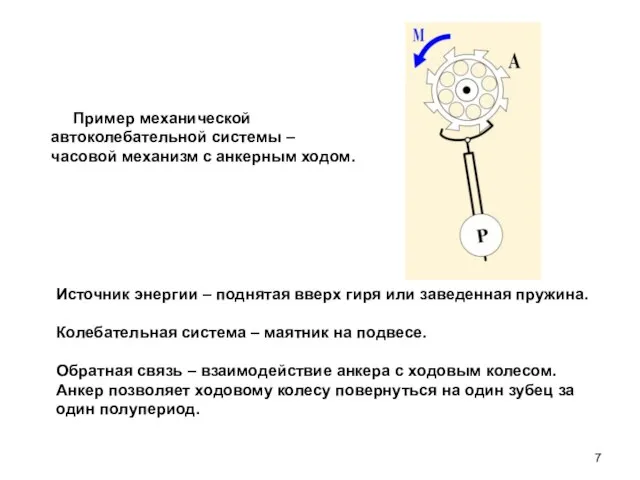
Пример механической автоколебательной системы – часовой механизм с анкерным ходом.
Источник энергии – поднятая вверх гиря или заведенная пружина.
Колебательная система – маятник на подвесе.
Обратная связь – взаимодействие анкера с ходовым колесом.
Анкер позволяет ходовому колесу повернуться на один зубец за один полупериод.

5.10. Волновые процессы. Продольные и поперечные волны
Волновым процессом или волной называется процесс распространения колебаний в сплошной среде.
Основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.
Типы волн:
волны на поверхности жидкости,
упругие волны,
электромагнитные волны.

Упругими волнами (или механическими) называются механические возмущения, распространяющиеся в упругой среде.
Упругие волны бывают продольные и поперечные.
В продольных волнах частицы среды колеблются в направлении распространения волны,
В поперечных — в плоскостях, перпендикулярных направлению распространения волны.

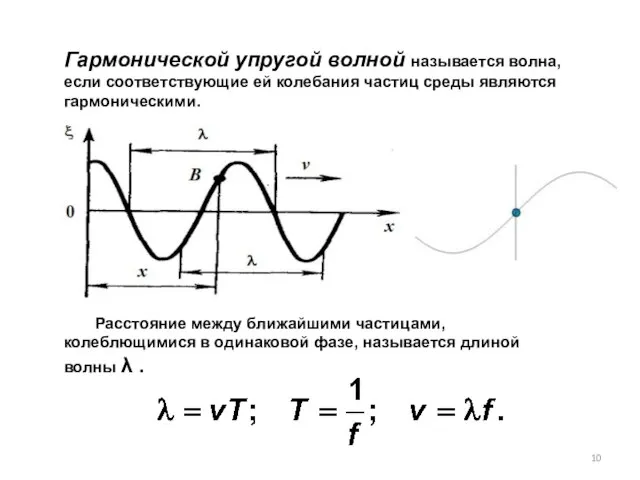
Гармонической упругой волной называется волна, если соответствующие ей колебания частиц среды являются гармоническими.
Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны λ .

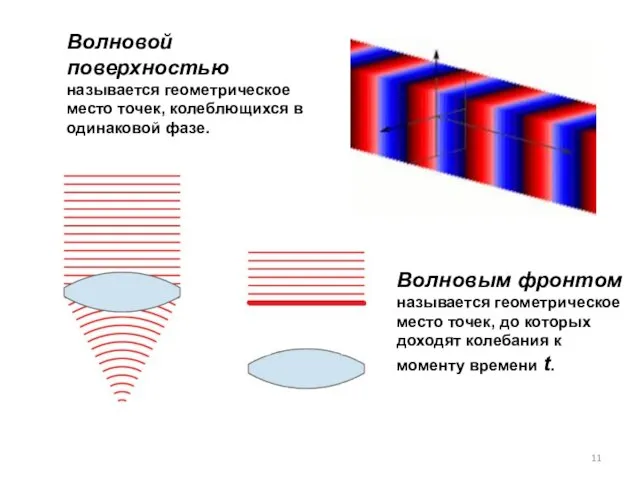
Волновым фронтом называется геометрическое место точек, до которых доходят колебания к моменту времени t.
Волновой поверхностью называется геометрическое место точек, колеблющихся в одинаковой фазе.

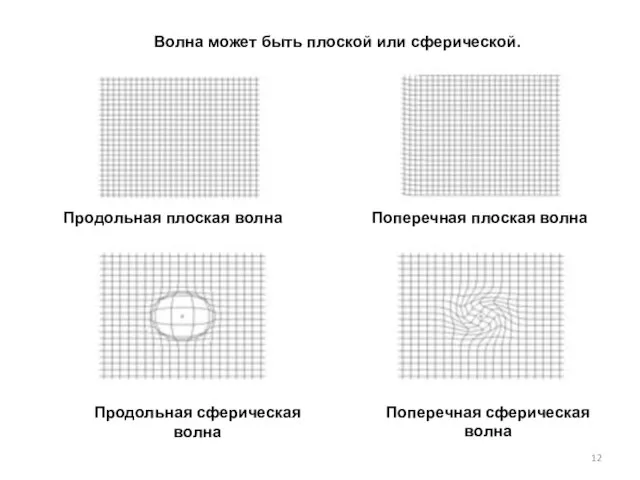
Волна может быть плоской или сферической.
Продольная плоская волна
Поперечная плоская волна
Продольная сферическая волна
Поперечная сферическая волна

Бегущими волнами называются волны, которые переносят в пространстве энергию.
Перенос энергии волнами характеризуется вектором плотности потока энергии (вектор Умова).
5.11. Уравнение бегущей волны. Фазовая скорость. Волновое уравнение.
Русский физик, философ, Николай Алексеевич Умов (1846—1915)
Направление вектора Умова совпадает с направлением переноса энергии.
Модуль вектора равен энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны.

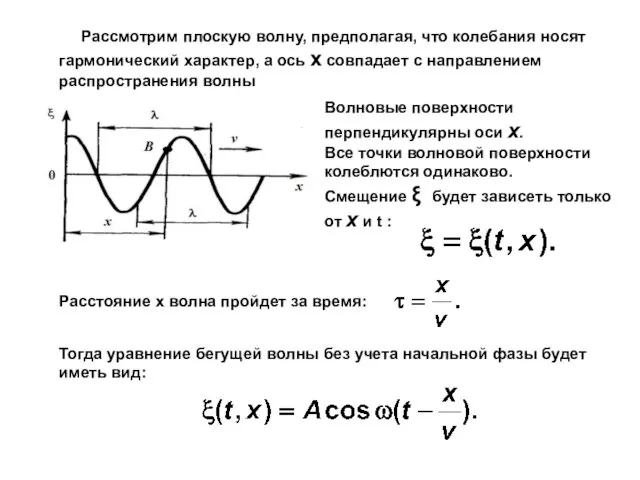
Рассмотрим плоскую волну, предполагая, что колебания носят гармонический характер, а ось х совпадает с направлением распрост­ранения волны
Волновые поверхности перпендикулярны оси х.
Все точки волновой поверхности колеблются одинаково.
Сме­щение ξ будет зависеть только от x и t :
Расстояние x волна пройдет за время:
Тогда уравнение бегущей волны без учета начальной фазы будет иметь вид:

Для характеристики волн используется волновое число:
Фазовой скоростью называется скорость перемещения волны:
Полное уравнение бегущей волны с учетом начальной фазы:
С учетом k уравнение бегущей волны будет иметь вид:

Уравнение сферической бегущей волны:
r — расстояние от центра волны до рассматриваемой точки среды
Фазовая скорость волны зависит от частоты волны:
Это явление называют дисперсией волн, а среда, в которой наблюдается дисперсия волн, называется диспергирующей средой.

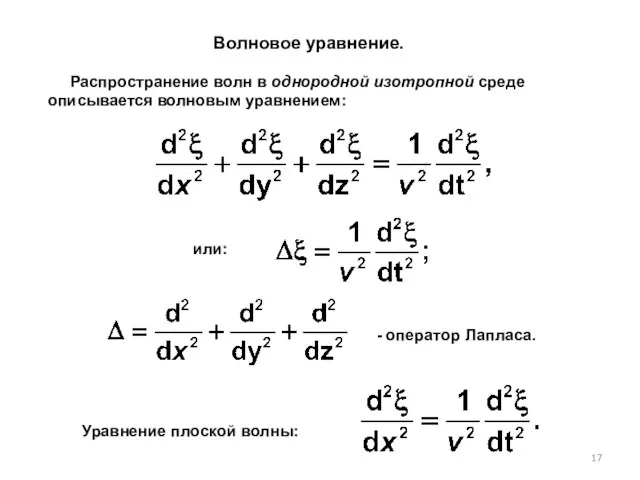
Распространение волн в однородной изотропной среде описывается волновым уравнением:
- оператор Лапласа.
Уравнение плоской волны:
Волновое уравнение.
или:

5.12. Интерференция волн.
Когерент­ными называются волны, если разность их фаз остается постоянной во времени.
Когерент­ными могут быть лишь волны, имеющие одинаковую частоту.
Наложение когерентных волн вызывает усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих воли.
Это явление называется интерференцией волн.

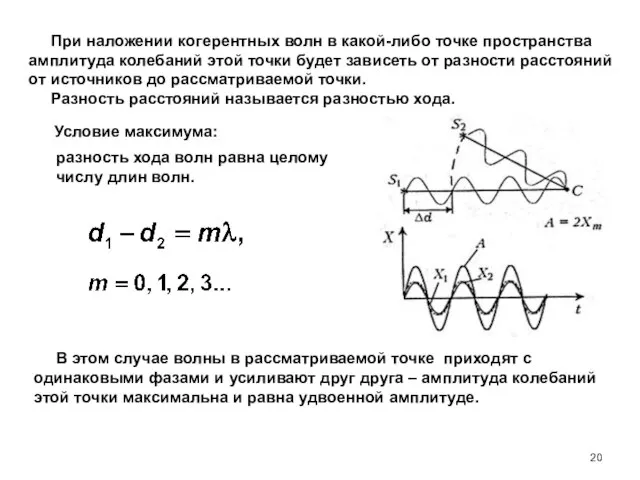
d1 и d2 — расстояния от источников волн до рассматриваемой точки C, k — волновое число, ϕ1 и ϕ2 — начальные фазы обеих накладывающихся сферических волн.
Рассмотрим наложение двух когерентных сферических волн, возбуждаемых точечными источниками S1 и S2 .

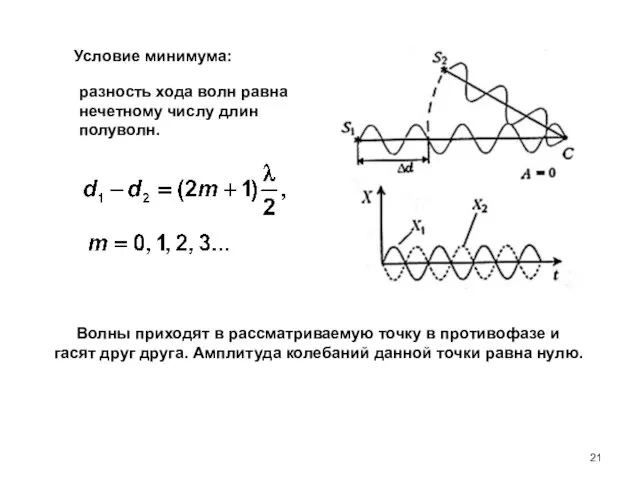
Условие максимума:
разность хода волн равна целому числу длин волн.
При наложении когерентных волн в какой-либо точке пространства амплитуда колебаний этой точки будет зависеть от разности расстояний от источников до рассматриваемой точки.
Разность расстояний называется разностью хода.
В этом случае волны в рассматриваемой точке приходят с одинаковыми фазами и усиливают друг друга – амплитуда колебаний этой точки максимальна и равна удвоенной амплитуде.

разность хода волн равна нечетному числу длин полуволн.
Волны приходят в рассматриваемую точку в противофазе и гасят друг друга. Амплитуда колебаний данной точки равна нулю.
Условие минимума:

Стоячие волны
Другой частный случай интерференции - стоячие волны.
Стоячие волны образуются при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами.
Две плоские волны распространяются навстречу друг другу вдоль оси х в среде без затухания (одинаковые амплитуды и частоты).
Уравнение стоячей волны.

Сложим уравнения прямой и обратной волн и получим уравнение стоячей волны:
Точки, в которых амплитуда колебаний максимальна, называются пучностями стоячей волны, а точки, в которых амплитуда колебаний равна нулю, называются узлами стоячей волны.

Амплитуда стоячей волны изменяется и определяется выражением:
В точке, где:
амплитуда колебаний достигает максимального значения, равного 2А.
В точке, где:
амплитуда колебаний обращается в нуль.

Координаты пучностей и узлов можно получить из записанных уравнений:
Из этих выражений следует, что расстояния между двумя соседними пучностями и двумя соседними узлами одинаковы и равны:
Расстояние между соседними пучностью и узлом стоячей волны равно:

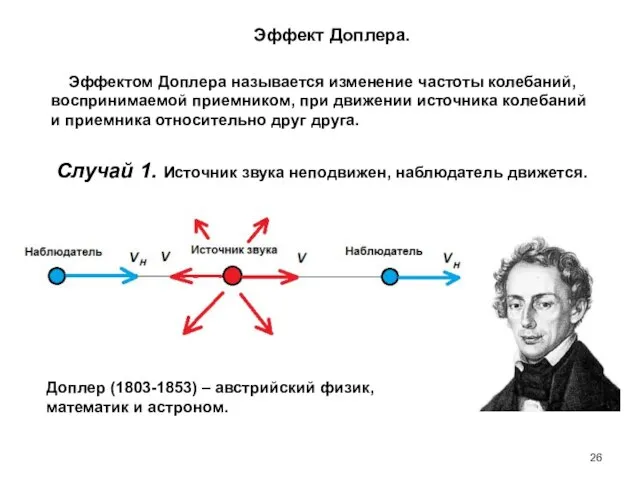
Эффект Доплера.
Доплер (1803-1853) – австрийский физик, математик и астроном.
Эффектом Доплера называется изменение частоты колебаний, воспринимаемой приемником, при движении источника колебаний и приемника относительно друг друга.
Случай 1. Источник звука неподвижен, наблюдатель движется.

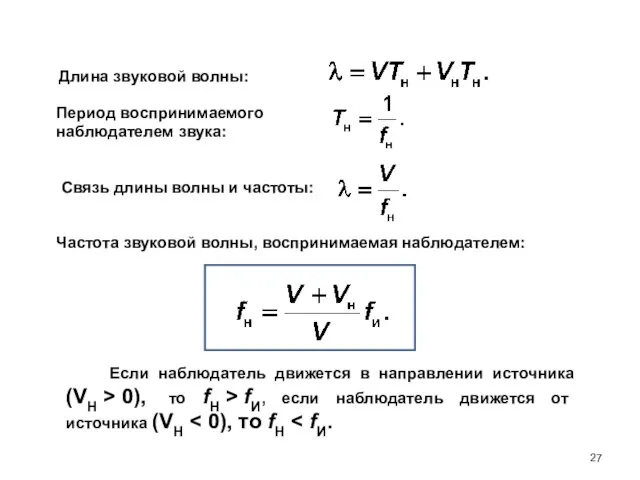
Длина звуковой волны:
Период воспринимаемого наблюдателем звука:
Связь длины волны и частоты:
Частота звуковой волны, воспринимаемая наблюдателем:
Если наблюдатель движется в направлении источника (VН > 0), то fН > fИ, если наблюдатель движется от источника (VН < 0), то fН < fИ.

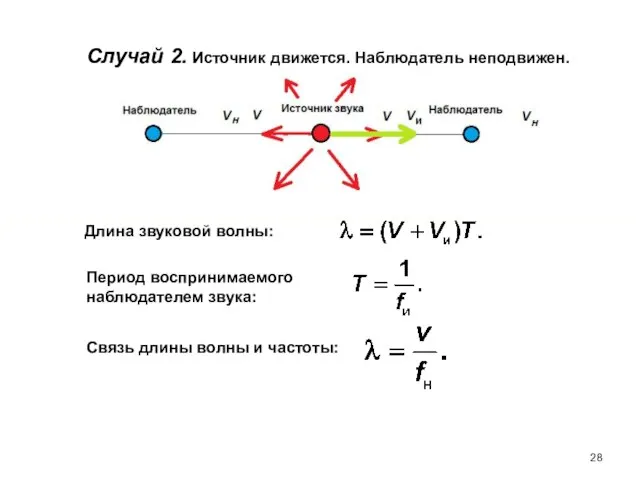
Случай 2. Источник движется. Наблюдатель неподвижен.
Длина звуковой волны:
Период воспринимаемого наблюдателем звука:
Связь длины волны и частоты:

Частота звуковой волны, воспринимаемая наблюдателем:
Если источник удаляется от наблюдателя, то Vи > 0 и, следовательно, fН < fИ. Если источник приближается к наблюдателю, то Vи < 0 и fН > fИ.