Содержание
- 2. Введение
- 3. 0. Введение. Общие сведения. Объем курса – 34 часа лекции 24 часа лабораторные занятия 14 часов
- 4. 0. Введение. Цели и задачи дисциплины. Ознакомить с фундаментальными основами дисциплины «Исследование операций», методами и конструктивными
- 5. 0. Введение. Литература. Основная Таха Х. Введение в исследование операций.: Пер. с англ. – М.: Издательский
- 6. 0. Введение. 0.1. Предмет дисциплины. Исследование операций – дисциплина, изучающая методы построения последовательности действий (операций), приводящих
- 7. 0. Введение. 0.1 Основные понятия. Изменяемые переменные (переменные решения – decision variables) – переменные, оптимальные значения
- 8. 0. Введение. 0.1. Основные понятия. Ограничения (constraints) – неравенства или равенства, определяющие область допустимых значений (ОДЗ)
- 9. 0. Введение. 0.1. Основные понятия. Математическая модель (model) – результат формализации задачи исследования операций. Включает в
- 10. 0. Введение. 0.2. Задача выбора операторов мобильной связи и тарифных планов. Предположим, что нам необходимо выбрать
- 11. 0. Введение. 0.2. Задача выбора операторов мобильной связи и тарифных планов. Варьируемые параметры и целевая функция
- 12. 0. Введение. 0.2. Задача выбора операторов мобильной связи и тарифных планов. Структура месячных затрат (Velcom и
- 13. 0. Введение. 0.2. Задача выбора операторов мобильной связи и тарифных планов. Структура месячных затрат (Belcel) Затраты
- 14. 0. Введение. 0.2. Задача выбора операторов мобильной связи и тарифных планов. Ограничения Ограничения в нашем случае
- 15. 0. Введение. 0.2. Задача выбора операторов мобильной связи и тарифных планов. Математическая модель задачи Окончательно математическая
- 16. 0. Введение. 0.2. Задача выбора операторов мобильной связи и тарифных планов. Алгоритм и программная реализация Учитывая
- 17. 0. Введение. 0.2. Задача выбора операторов мобильной связи и тарифных планов. Некоторые замечания Как это обычно
- 18. 0. Введение. 0.3. Многовариантность математических моделей. Задача нахождения коробки максимального объема заданной площади поверхности Рассмотрим почти
- 19. 0. Введение. 0.3. Многовариантность математических моделей. Задача нахождения коробки требуемого объема заданной площади поверхности Модифицируем задачу:
- 20. 0. Введение. 0.3. Многовариантность математических моделей. Задача нахождения коробки требуемого объема заданной площади поверхности Переформулируем математическую
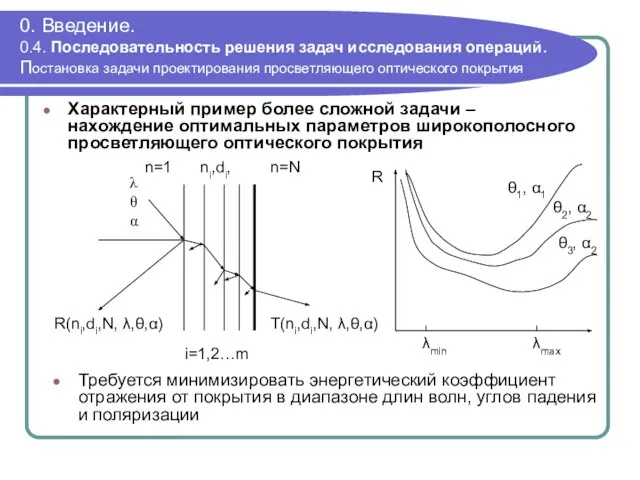
- 21. 0. Введение. 0.4. Последовательность решения задач исследования операций. Постановка задачи проектирования просветляющего оптического покрытия Характерный пример
- 22. 0. Введение. 0.4. Последовательность решения задач исследования операций. Формализация задачи Пусть покрытие состоит из непоглощающих диэлектрических
- 23. 0. Введение. 0.4. Последовательность решения задач исследования операций. Математическая модель
- 24. 0. Введение. 0.5. Структурная и параметрическая оптимизация Процедура поиска оптимального решения может быть реализована двумя способами:
- 25. 0. Введение. 0.6. Методы исследования операций Все модели исследования операций можно разделить на группы по следующим
- 26. 0. Введение. 0.6. Методы исследования операций Наука и искусство Этапы реализации методов исследования операций: Формализация исходной
- 27. 0. Введение. 0.7. Этапы реализации методов исследования операций Формализация исходной проблемы предполагает исследование предметной области, где
- 28. 0. Введение. 0.7. Этапы реализации методов исследования операций Поиск оптимального решения (решение модели) Применение известных методов
- 29. Линейное программирование
- 30. 1. Линейное программирование 1.1. Постановка задачи Линейное программирование (ЛП) – это метод математического моделирования, разработанный для
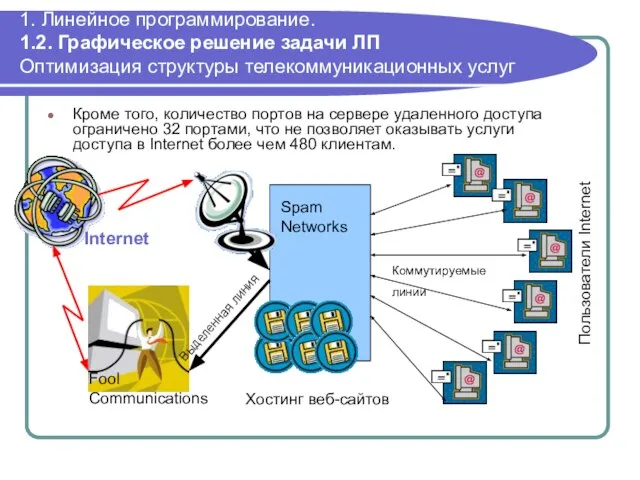
- 31. 1. Линейное программирование. 1.2. Графическое решение задачи ЛП Оптимизация структуры телекоммуникационных услуг Телекоммуникационная компания Spam Networks
- 32. 1. Линейное программирование. 1.2. Графическое решение задачи ЛП Оптимизация структуры телекоммуникационных услуг Кроме того, количество портов
- 33. 1. Линейное программирование. 1.2. Графическое решение задачи ЛП Оптимизация структуры телекоммуникационных услуг: формализация исходной проблемы Множество
- 34. 1. Линейное программирование. 1.2. Графическое решение задачи ЛП Оптимизация структуры телекоммуникационных услуг: математическая модель max F(x1,
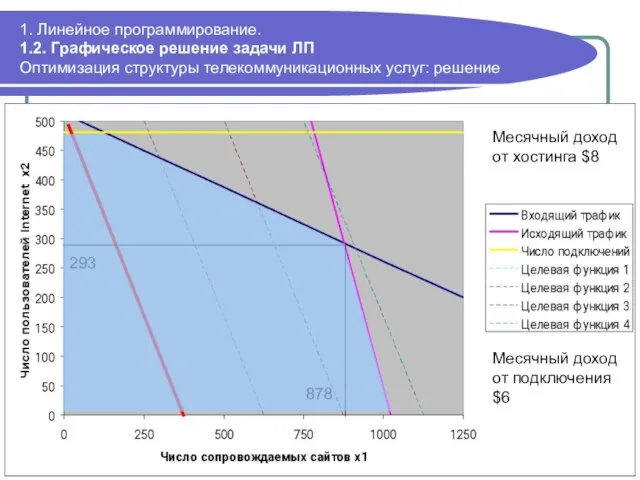
- 35. 1. Линейное программирование. 1.2. Графическое решение задачи ЛП Оптимизация структуры телекоммуникационных услуг: решение 293 878 Месячный
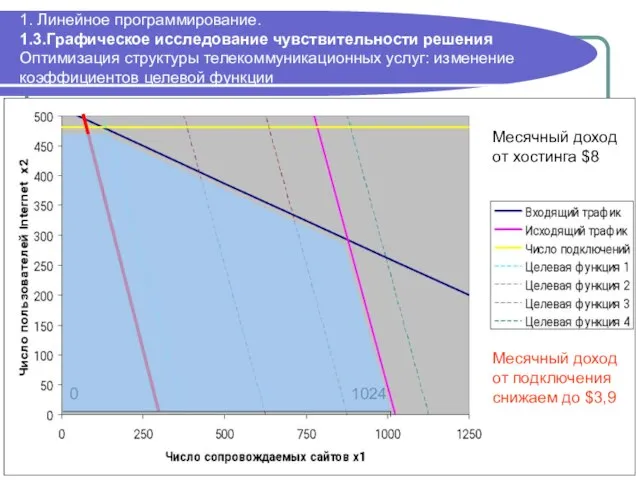
- 36. 1. Линейное программирование. 1.3.Графическое исследование чувствительности решения Оптимизация структуры телекоммуникационных услуг: изменение коэффициентов целевой функции 0
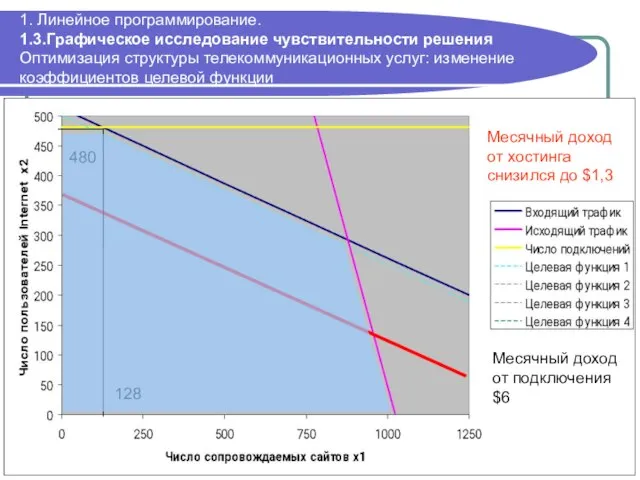
- 37. 1. Линейное программирование. 1.3.Графическое исследование чувствительности решения Оптимизация структуры телекоммуникационных услуг: изменение коэффициентов целевой функции 480
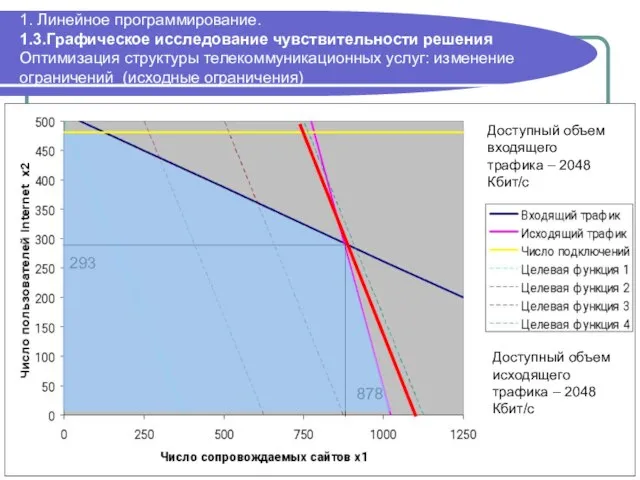
- 38. 1. Линейное программирование. 1.3.Графическое исследование чувствительности решения Оптимизация структуры телекоммуникационных услуг: изменение ограничений (исходные ограничения) 293
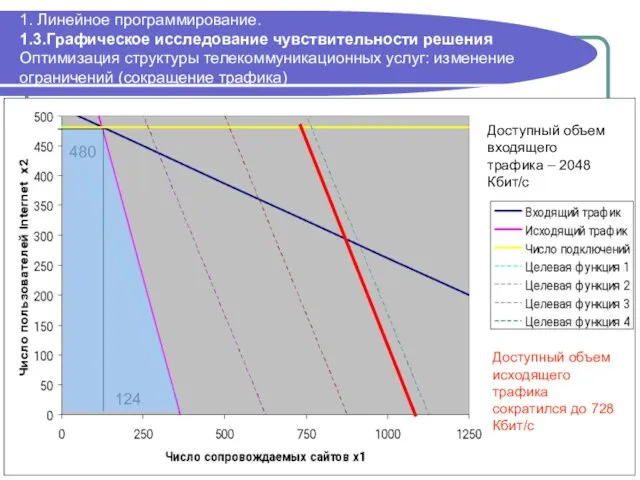
- 39. 1. Линейное программирование. 1.3.Графическое исследование чувствительности решения Оптимизация структуры телекоммуникационных услуг: изменение ограничений (сокращение трафика) 480
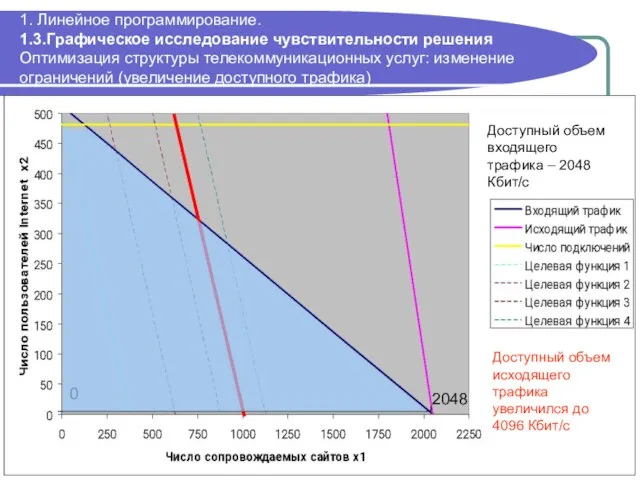
- 40. 1. Линейное программирование. 1.3.Графическое исследование чувствительности решения Оптимизация структуры телекоммуникационных услуг: изменение ограничений (увеличение доступного трафика)
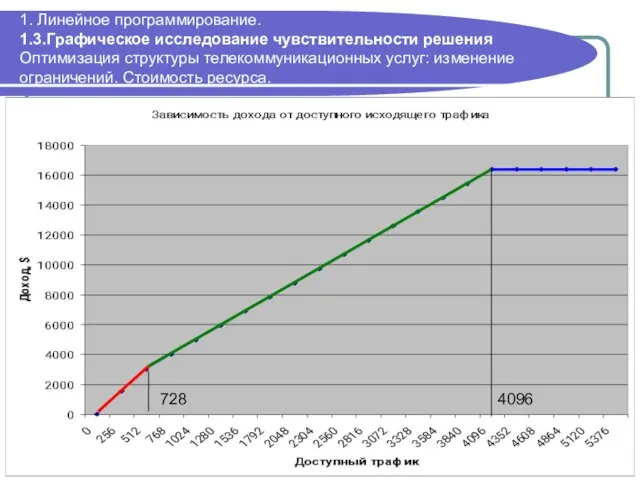
- 41. 1. Линейное программирование. 1.3.Графическое исследование чувствительности решения Оптимизация структуры телекоммуникационных услуг: изменение ограничений. Стоимость ресурса. 728
- 42. 1. Линейное программирование. 1.4.Принципы построения аналитических методов решения задачи ЛП Оптимизация структуры телекоммуникационных услуг: Анализ результатов
- 43. 1. Линейное программирование. 1.4.Принципы построения аналитических методов решения задачи ЛП Методика поиска оптимального решения Оптимальное решение
- 44. 1. Линейное программирование. 1.5.Стандартная форма задачи ЛП шаг 1 Все ограничения (включая ограничения неотрицательности переменных) преобразуются
- 45. 1. Линейное программирование. 1.5.Стандартная форма задачи ЛП шаг 2 Все варьируемые переменные должны быть неотрицательными. Преобразование
- 46. 1. Линейное программирование. 1.5.Стандартная форма задачи ЛП шаг 3 Целевую функцию следует минимизировать или максимизировать Задача
- 47. 1. Линейное программирование. 1.5.Стандартная форма задачи ЛП Математическая модель в стандартной форме max F(x1, x2); F(x1,
- 48. 1. Линейное программирование. 1.5.Стандартная форма задачи ЛП Математическая модель в стандартной форме (после переобозначения переменных)
- 49. 1. Линейное программирование. 1.6.Понятие базисного решения задачи ЛП Допустимые базисные решения Задача ЛП в стандартной форме
- 50. 1. Линейное программирование. 1.6.Понятие базисного решения задачи ЛП Свободные переменные и базисные решения Свободные переменные мы
- 51. 1. Линейное программирование. 1.7. Основы симплекс-метода Идея алгоритма Можно доказать, что решение задачи ЛП может достигаться
- 52. 1. Линейное программирование. 1.7. Основы симплекс-метода Оптимизация структуры телекоммуникационных услуг. Математическая модель. Вспомним математическую формулировку задачи
- 53. 1. Линейное программирование. 1.7. Основы симплекс-метода Оптимизация структуры телекоммуникационных услуг. Система уравнений Перепишем уравнения в виде:
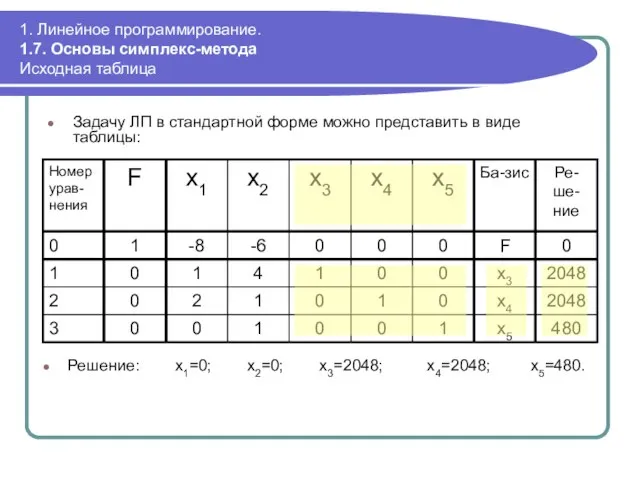
- 54. 1. Линейное программирование. 1.7. Основы симплекс-метода Исходная таблица Задачу ЛП в стандартной форме можно представить в
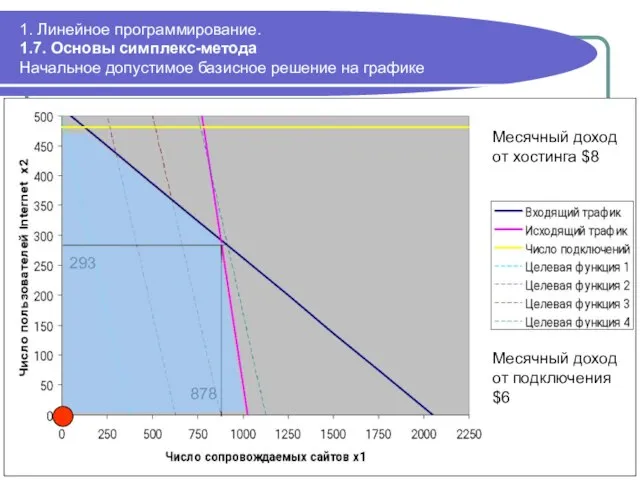
- 55. 1. Линейное программирование. 1.7. Основы симплекс-метода Начальное допустимое базисное решение на графике 293 878 Месячный доход
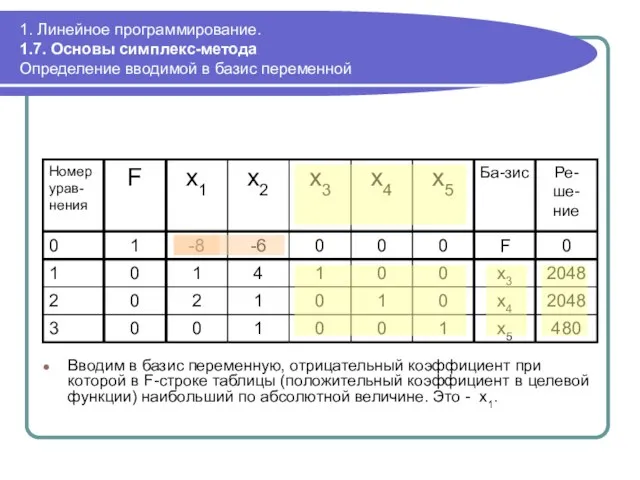
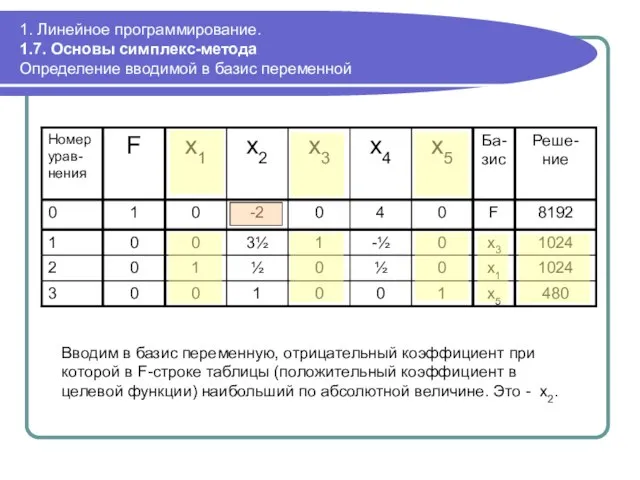
- 56. 1. Линейное программирование. 1.7. Основы симплекс-метода Определение вводимой в базис переменной Вводим в базис переменную, отрицательный
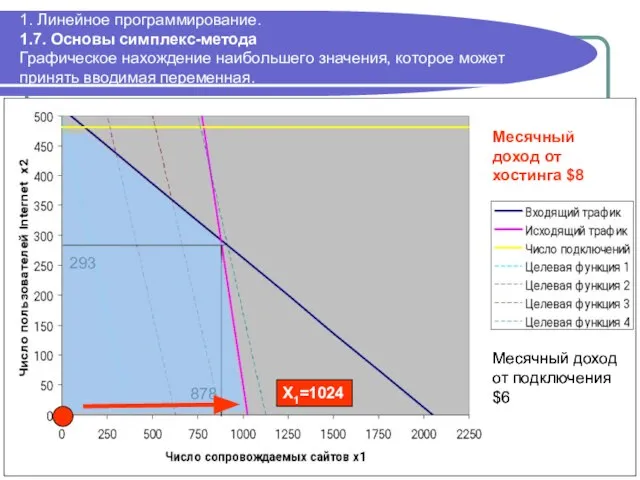
- 57. 293 878 Месячный доход от подключения $6 1. Линейное программирование. 1.7. Основы симплекс-метода Графическое нахождение наибольшего
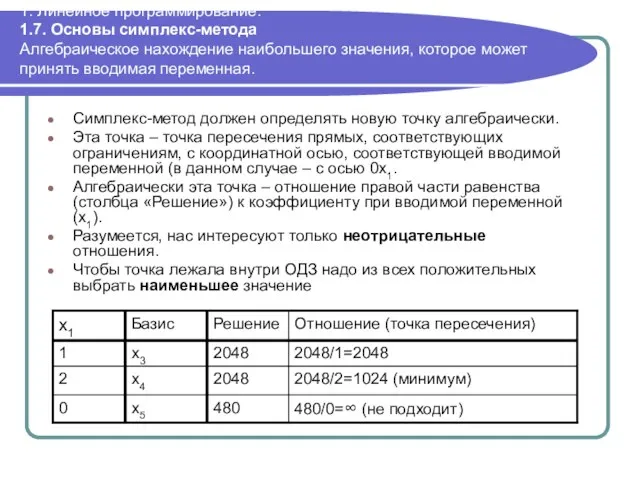
- 58. 1. Линейное программирование. 1.7. Основы симплекс-метода Алгебраическое нахождение наибольшего значения, которое может принять вводимая переменная. Симплекс-метод
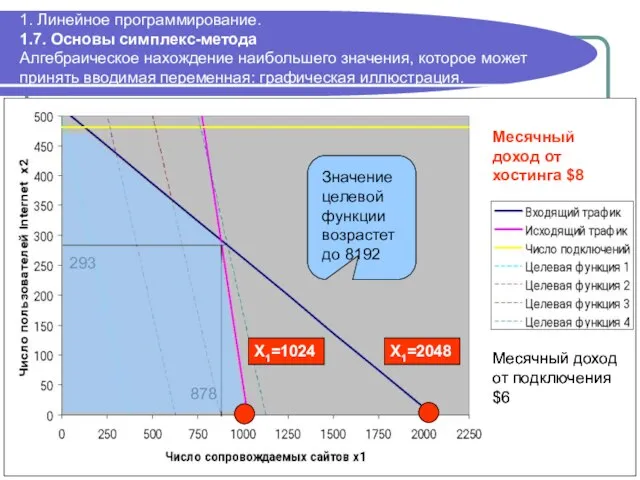
- 59. 293 878 Месячный доход от подключения $6 1. Линейное программирование. 1.7. Основы симплекс-метода Алгебраическое нахождение наибольшего
- 60. 1. Линейное программирование. 1.7. Основы симплекс-метода Выбор исключаемой из базиса переменной Исключается та переменная, которой в
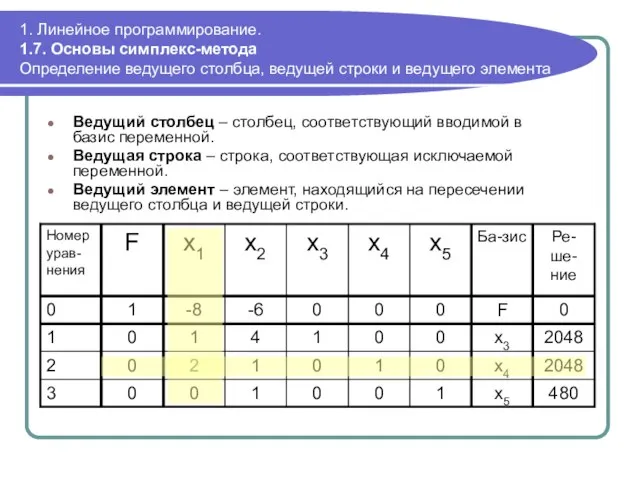
- 61. 1. Линейное программирование. 1.7. Основы симплекс-метода Определение ведущего столбца, ведущей строки и ведущего элемента Ведущий столбец
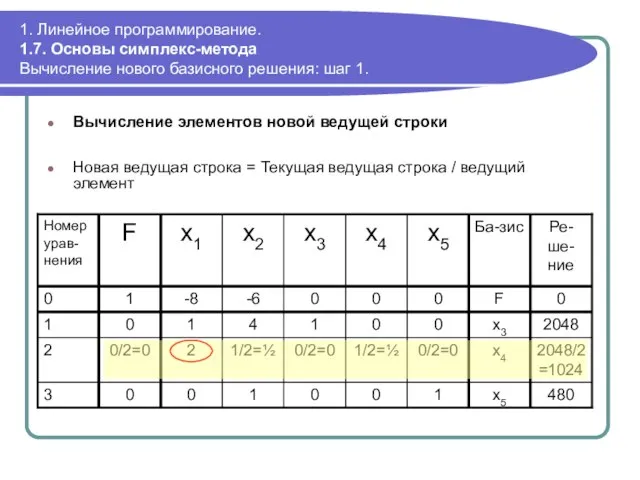
- 62. 1. Линейное программирование. 1.7. Основы симплекс-метода Вычисление нового базисного решения: шаг 1. Вычисление элементов новой ведущей
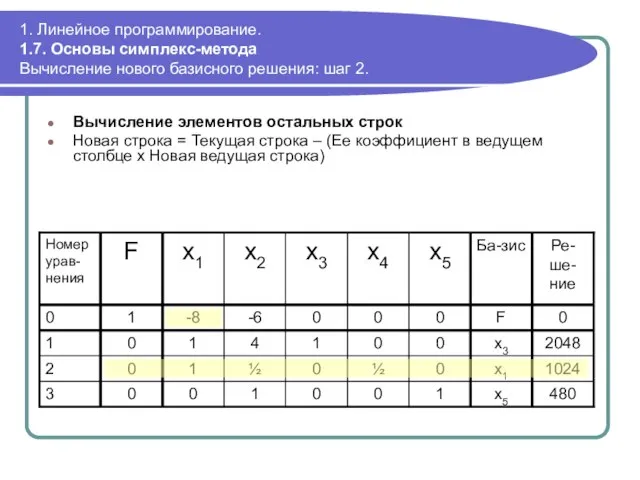
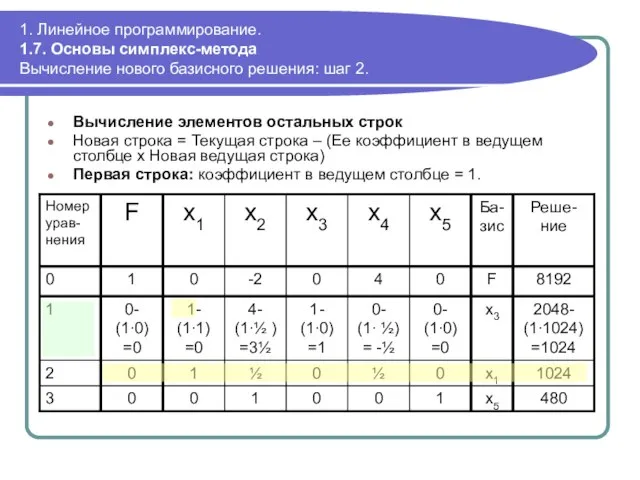
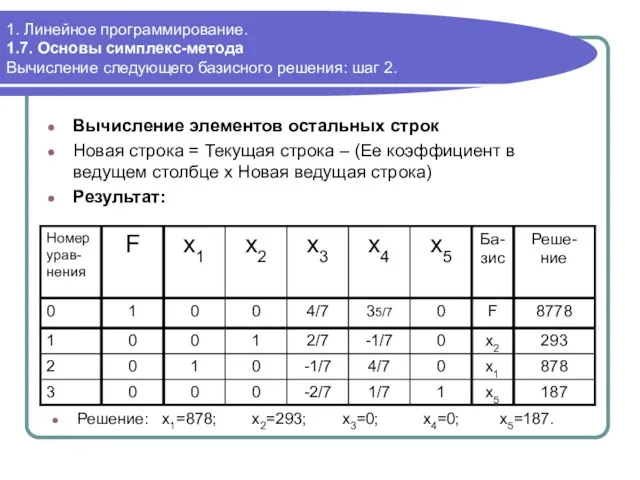
- 63. 1. Линейное программирование. 1.7. Основы симплекс-метода Вычисление нового базисного решения: шаг 2. Вычисление элементов остальных строк
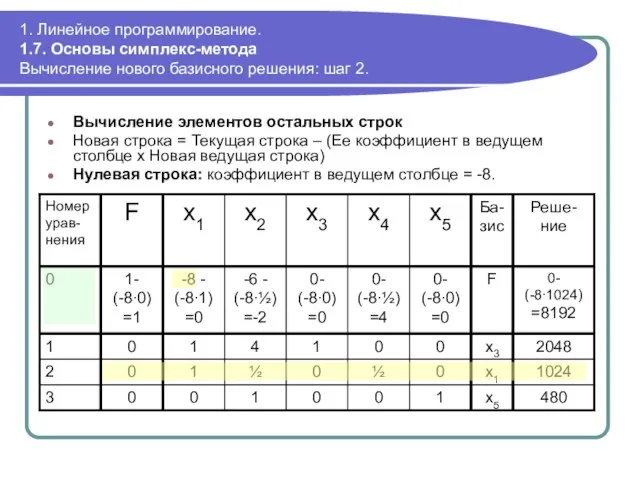
- 64. 1. Линейное программирование. 1.7. Основы симплекс-метода Вычисление нового базисного решения: шаг 2. Вычисление элементов остальных строк
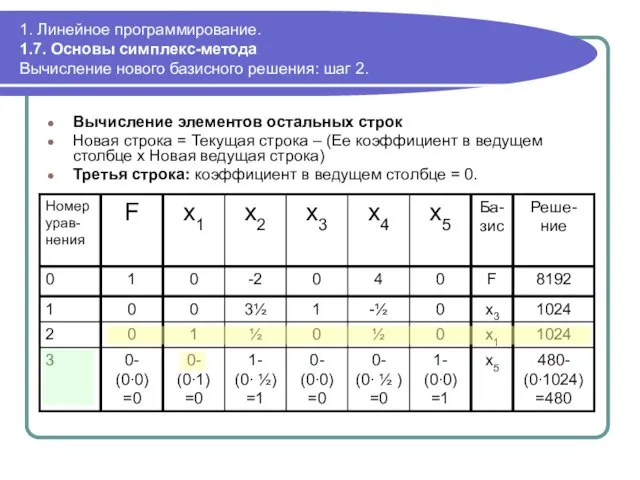
- 65. 1. Линейное программирование. 1.7. Основы симплекс-метода Вычисление нового базисного решения: шаг 2. Вычисление элементов остальных строк
- 66. 1. Линейное программирование. 1.7. Основы симплекс-метода Вычисление нового базисного решения: шаг 2. Вычисление элементов остальных строк
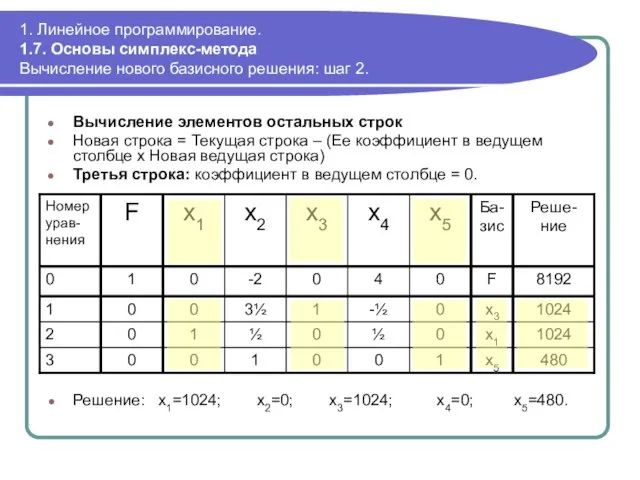
- 67. 1. Линейное программирование. 1.7. Основы симплекс-метода Вычисление нового базисного решения: шаг 2. Вычисление элементов остальных строк
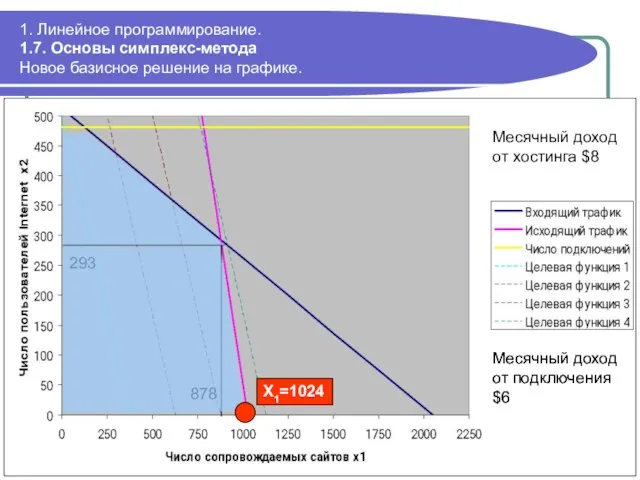
- 68. 293 878 Месячный доход от подключения $6 1. Линейное программирование. 1.7. Основы симплекс-метода Новое базисное решение
- 69. 1. Линейное программирование. 1.7. Основы симплекс-метода Определение вводимой в базис переменной Вводим в базис переменную, отрицательный
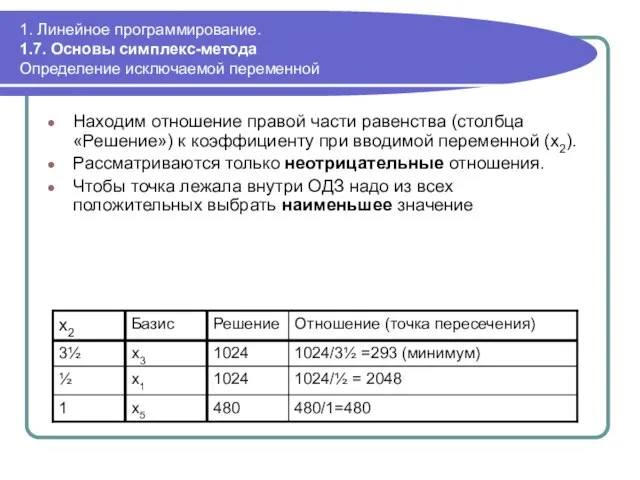
- 70. 1. Линейное программирование. 1.7. Основы симплекс-метода Определение исключаемой переменной Находим отношение правой части равенства (столбца «Решение»)
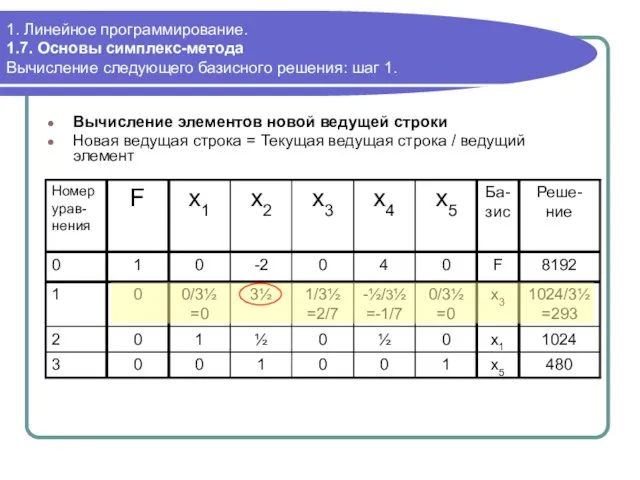
- 71. 1. Линейное программирование. 1.7. Основы симплекс-метода Вычисление следующего базисного решения: шаг 1. Вычисление элементов новой ведущей
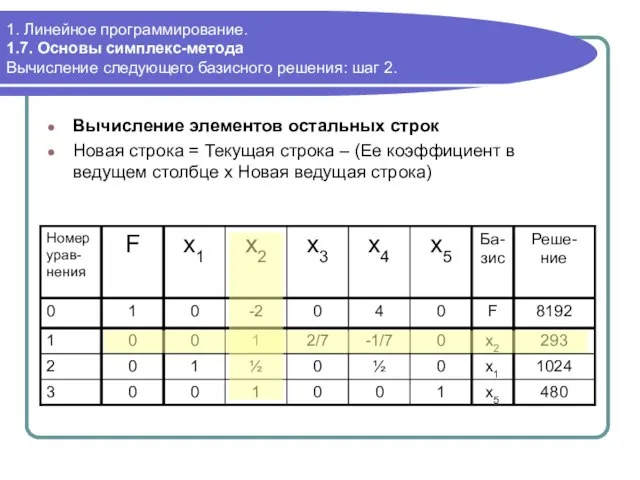
- 72. 1. Линейное программирование. 1.7. Основы симплекс-метода Вычисление следующего базисного решения: шаг 2. Вычисление элементов остальных строк
- 73. 1. Линейное программирование. 1.7. Основы симплекс-метода Вычисление следующего базисного решения: шаг 2. Вычисление элементов остальных строк
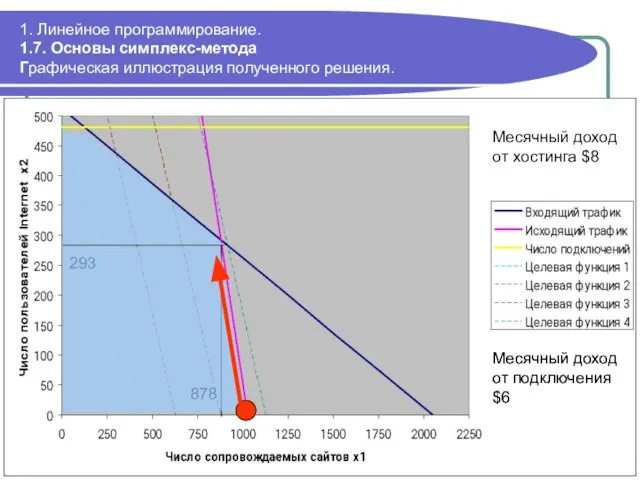
- 74. 293 878 Месячный доход от подключения $6 1. Линейное программирование. 1.7. Основы симплекс-метода Графическая иллюстрация полученного
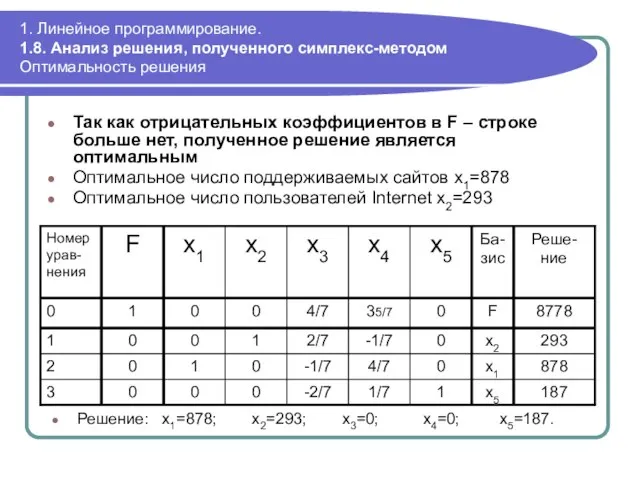
- 75. 1. Линейное программирование. 1.8. Анализ решения, полученного симплекс-методом Оптимальность решения Так как отрицательных коэффициентов в F
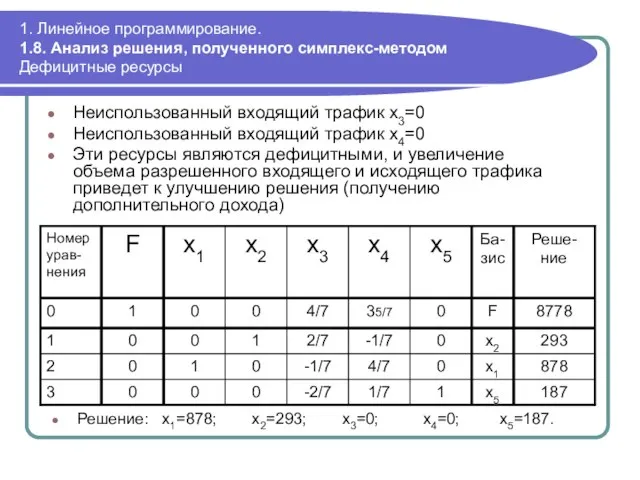
- 76. 1. Линейное программирование. 1.8. Анализ решения, полученного симплекс-методом Дефицитные ресурсы Неиспользованный входящий трафик x3=0 Неиспользованный входящий
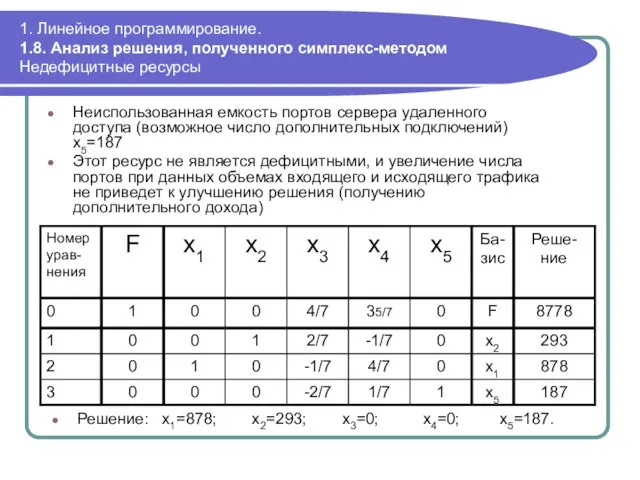
- 77. 1. Линейное программирование. 1.8. Анализ решения, полученного симплекс-методом Недефицитные ресурсы Неиспользованная емкость портов сервера удаленного доступа
- 78. 1. Линейное программирование. 1.9. Алгоритм симплекс-метода Базовый алгоритм Найти начальное допустимое базисное решение (полный алгоритм будет
- 79. 1. Линейное программирование. 1.9. Алгоритм симплекс-метода Правила выбора вводимых и исключаемых переменных Условие оптимальности. Вводимой переменной
- 80. 1. Линейное программирование. 1.10. Искусственное начальное решение Размещение данных для обработки в распределенной вычислительной среде В
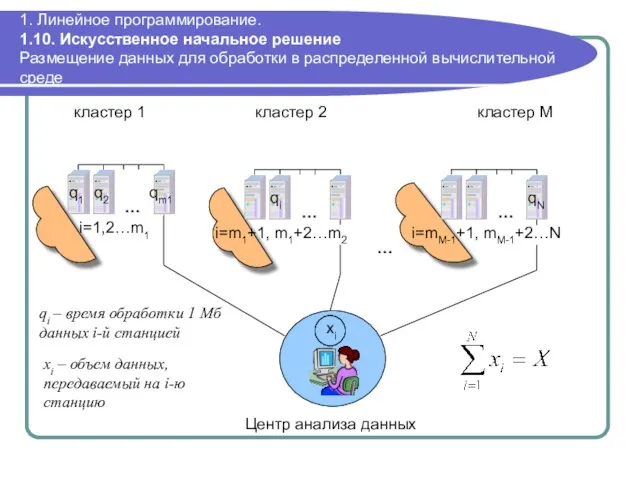
- 81. 1. Линейное программирование. 1.10. Искусственное начальное решение Размещение данных для обработки в распределенной вычислительной среде кластер
- 82. 1. Линейное программирование. 1.10. Искусственное начальное решение Размещение данных для обработки в распределенной вычислительной среде. Формализация
- 83. 1. Линейное программирование. 1.10. Искусственное начальное решение Размещение данных для обработки в распределенной вычислительной среде. Математическая
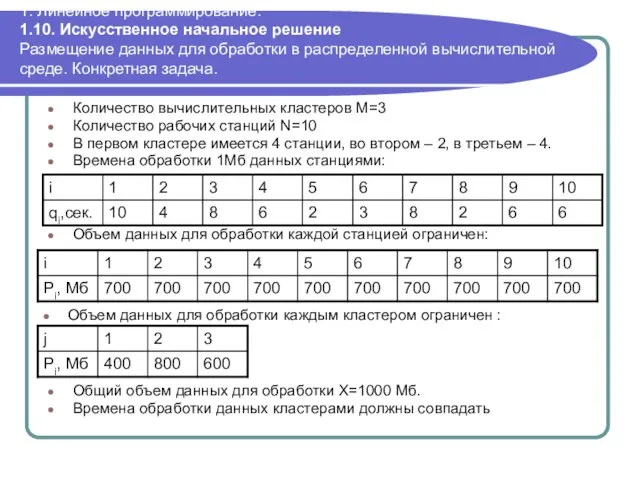
- 84. 1. Линейное программирование. 1.10. Искусственное начальное решение Размещение данных для обработки в распределенной вычислительной среде. Конкретная
- 85. 1. Линейное программирование. 1.10. Искусственное начальное решение Размещение данных для обработки в распределенной вычислительной среде. Математическая
- 86. 1. Линейное программирование. 1.10. Искусственное начальное решение Размещение данных для обработки в распределенной вычислительной среде. Приведение
- 87. 1. Линейное программирование. 1.10. Искусственное начальное решение Размещение данных для обработки в распределенной вычислительной среде. Искусственное
- 88. 1. Линейное программирование. 1.11. М-метод нахождения искусственного начального решения. Запишем задачу ЛП в стандартной форме. Для
- 89. 1. Линейное программирование. 1.11. М-метод нахождения искусственного начального решения. Пример использования М-метода: исходная задача и стандартная
- 90. 1. Линейное программирование. 1.11. М-метод нахождения искусственного начального решения. Пример использования М-метода: введение искусственных переменных min
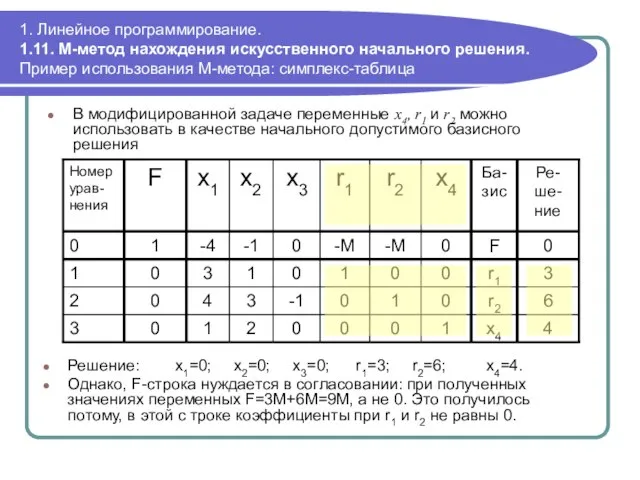
- 91. 1. Линейное программирование. 1.11. М-метод нахождения искусственного начального решения. Пример использования М-метода: симплекс-таблица В модифицированной задаче
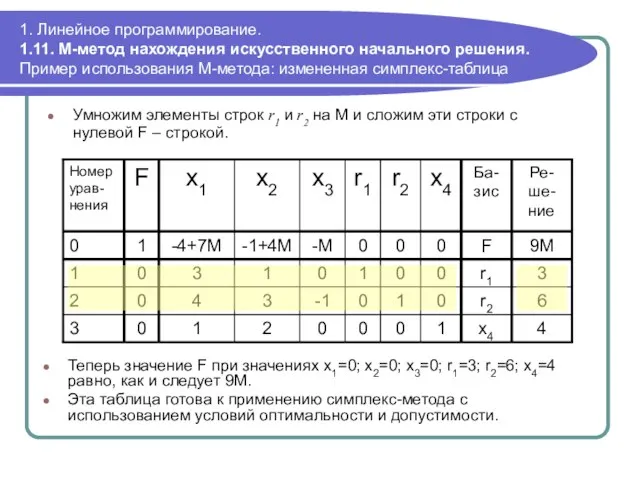
- 92. 1. Линейное программирование. 1.11. М-метод нахождения искусственного начального решения. Пример использования М-метода: измененная симплекс-таблица Умножим элементы
- 93. 1. Линейное программирование. 1.11. М-метод нахождения искусственного начального решения. Пример использования М-метода: решение Самостоятельно проделайте процедуру
- 94. 1. Линейное программирование. 1.11. М-метод нахождения искусственного начального решения. Некоторые замечания Использование штрафа M может не
- 95. 1. Линейное программирование. 1.12. Двухэтапный метод. Базовый алгоритм Найти допустимое базисное решение Записать задачу ЛП в
- 96. 1. Линейное программирование. 1.12. Двухэтапный метод. Пример использования двухэтапного метода. min F(x1, x2); F(x1, x2) =
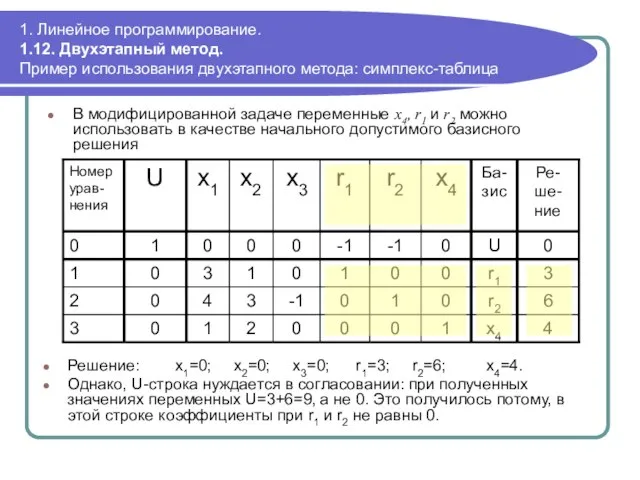
- 97. 1. Линейное программирование. 1.12. Двухэтапный метод. Пример использования двухэтапного метода: симплекс-таблица В модифицированной задаче переменные x4,
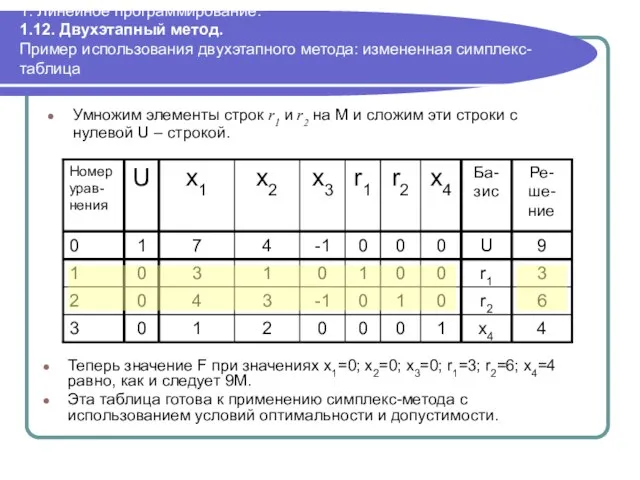
- 98. 1. Линейное программирование. 1.12. Двухэтапный метод. Пример использования двухэтапного метода: измененная симплекс-таблица Умножим элементы строк r1
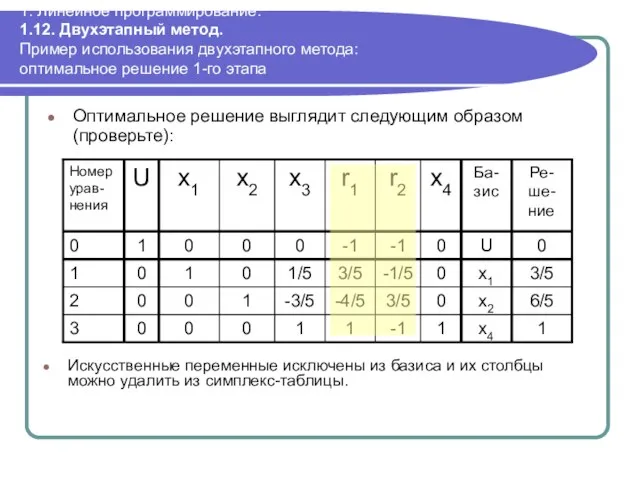
- 99. 1. Линейное программирование. 1.12. Двухэтапный метод. Пример использования двухэтапного метода: оптимальное решение 1-го этапа Оптимальное решение
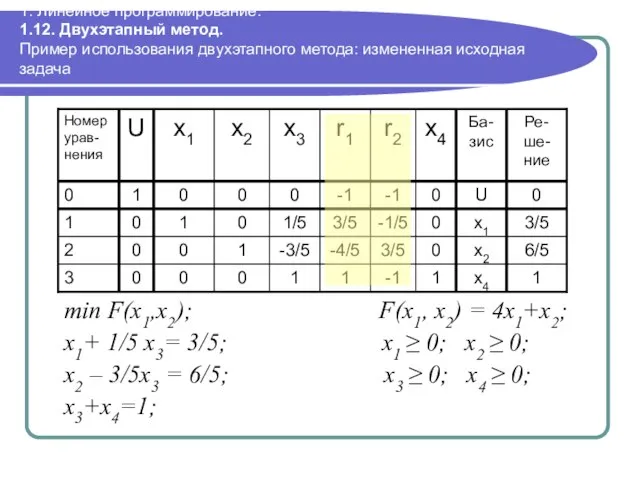
- 100. 1. Линейное программирование. 1.12. Двухэтапный метод. Пример использования двухэтапного метода: измененная исходная задача min F(x1,x2); F(x1,
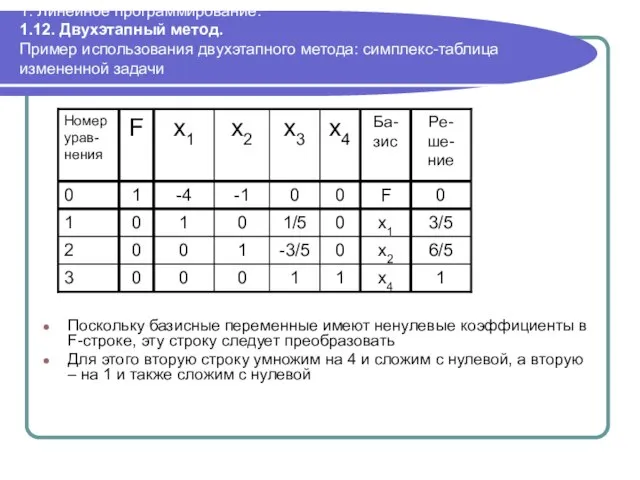
- 101. 1. Линейное программирование. 1.12. Двухэтапный метод. Пример использования двухэтапного метода: симплекс-таблица измененной задачи Поскольку базисные переменные
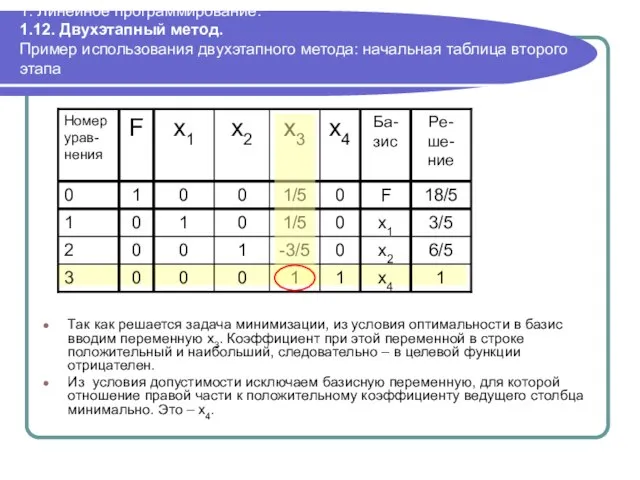
- 102. 1. Линейное программирование. 1.12. Двухэтапный метод. Пример использования двухэтапного метода: начальная таблица второго этапа Так как
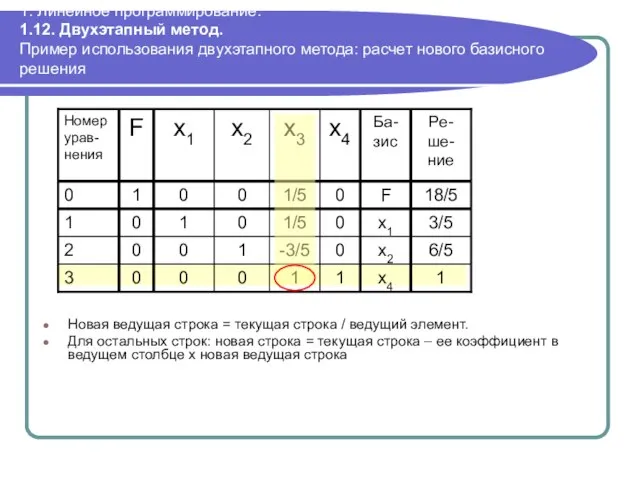
- 103. 1. Линейное программирование. 1.12. Двухэтапный метод. Пример использования двухэтапного метода: расчет нового базисного решения Новая ведущая
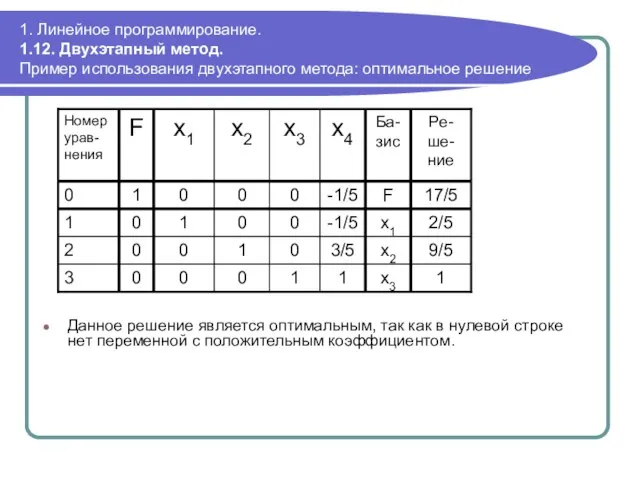
- 104. 1. Линейное программирование. 1.12. Двухэтапный метод. Пример использования двухэтапного метода: оптимальное решение Данное решение является оптимальным,
- 105. 1. Линейное программирование. 1.12. Двухэтапный метод. Замечания по применению Удаление искусственных переменных в конце первого этапа
- 106. 1. Линейное программирование. 1.13. Особые случаи применения симплекс-метода Вырожденность Альтернативные оптимальные решения Неограниченные решения Отсутствие допустимых
- 107. 1. Линейное программирование. 1.13. Особые случаи применения симплекс-метода Вырожденность В ходе выполнения симплекс-метода проверка условия допустимости
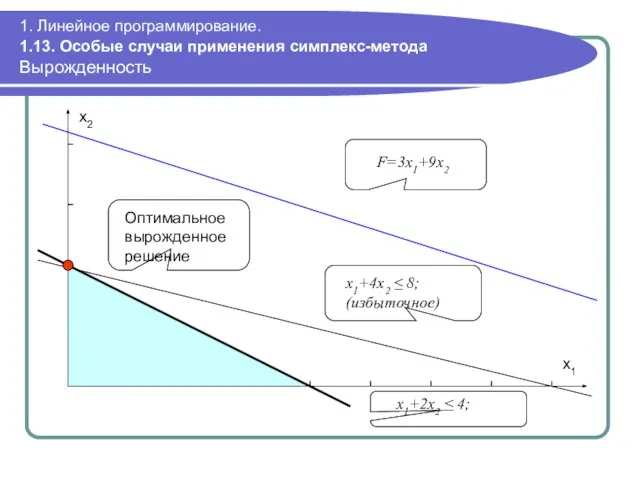
- 108. 1. Линейное программирование. 1.13. Особые случаи применения симплекс-метода Вырожденность Оптимальное вырожденное решение x1+2x2 ≤ 4; F=3x1+9x2
- 109. 1. Линейное программирование. 1.13. Особые случаи применения симплекс-метода Вырожденность Возможные последствия вырожденности: Зацикливание симплекс-метода (некоторая последовательность
- 110. 1. Линейное программирование. 1.13. Особые случаи применения симплекс-метода Альтернативные оптимальные решения Альтернативные оптимальные решения возникают, когда
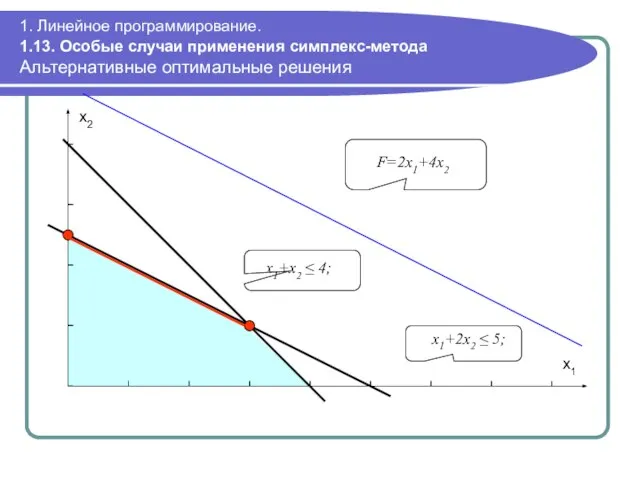
- 111. 1. Линейное программирование. 1.13. Особые случаи применения симплекс-метода Альтернативные оптимальные решения x1+2x2 ≤ 5; F=2x1+4x2 x2
- 112. 1. Линейное программирование. 1.13. Особые случаи применения симплекс-метода Неограниченные решения Если в процессе поиска решения значения
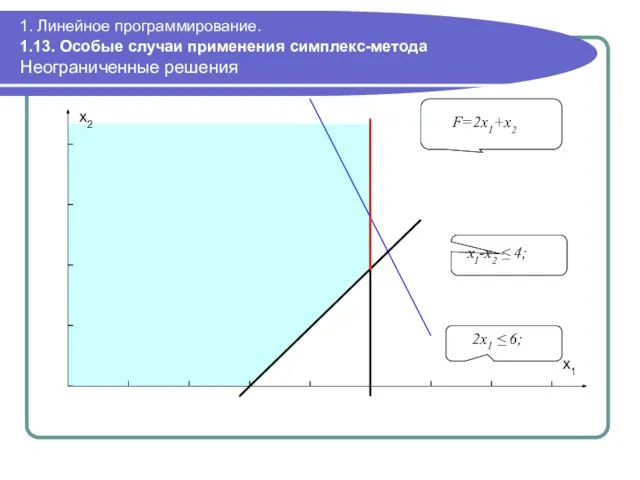
- 113. 1. Линейное программирование. 1.13. Особые случаи применения симплекс-метода Неограниченные решения 2x1 ≤ 6; F=2x1+x2 x2 x1
- 114. 1. Линейное программирование. 1.13. Особые случаи применения симплекс-метода Неограниченные решения Правило выявления неограниченности решения: Если на
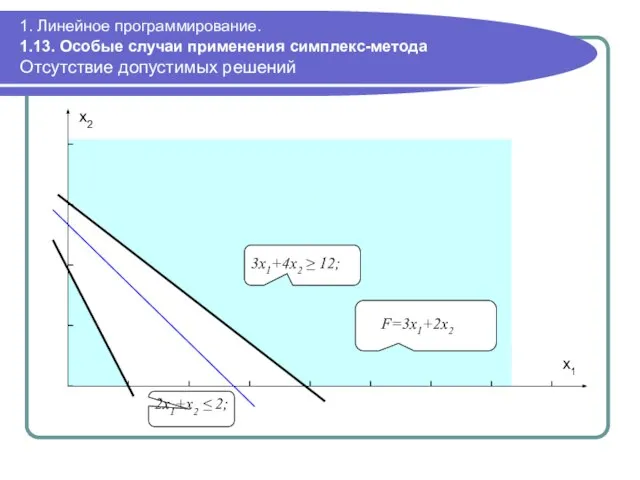
- 115. 1. Линейное программирование. 1.13. Особые случаи применения симплекс-метода Отсутствие допустимых решений Если ограничения задачи ЛП несовместны,
- 116. 1. Линейное программирование. 1.13. Особые случаи применения симплекс-метода Отсутствие допустимых решений 2x1+x2 ≤ 2; F=3x1+2x2 x2
- 117. 1. Линейное программирование. 1.14. Матричное представление стандартной задачи ЛП В матричной форме стандартную задачу ЛП можно
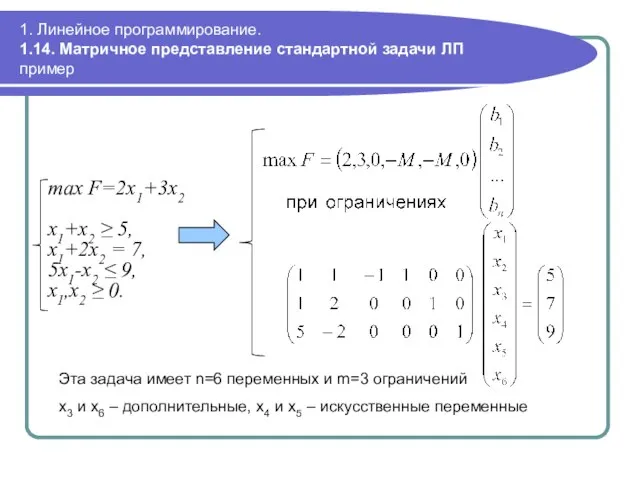
- 118. 1. Линейное программирование. 1.14. Матричное представление стандартной задачи ЛП пример max F=2x1+3x2 x1+x2 ≥ 5, x1+2x2
- 119. 1. Линейное программирование. 1.14. Матричное представление стандартной задачи ЛП Базисные решения Для системы из m уравнений
- 120. 1. Линейное программирование. 1.15. Матричное представление симплекс-таблиц Мы утверждаем, что конечное оптимальное решение задачи ЛП достигается
- 121. 1. Линейное программирование. 1.15. Матричное представление симплекс-таблиц Тогда стандартную задачу ЛП можно записать в следующем виде:
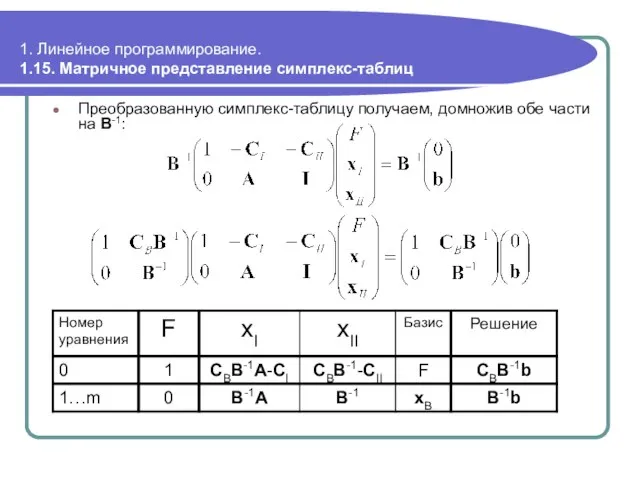
- 122. 1. Линейное программирование. 1.15. Матричное представление симплекс-таблиц Преобразованную симплекс-таблицу получаем, домножив обе части на B-1:
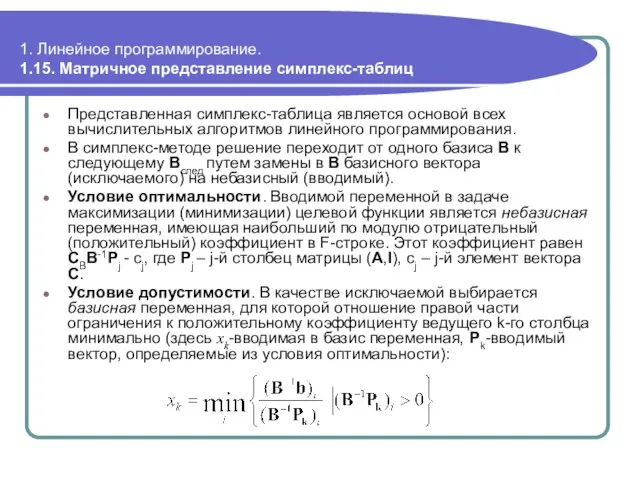
- 123. 1. Линейное программирование. 1.15. Матричное представление симплекс-таблиц Представленная симплекс-таблица является основой всех вычислительных алгоритмов линейного программирования.
- 124. 1. Линейное программирование. 1.16. Модифицированный симплекс-метод В модифицированном симплекс-методе вместо процедуры преобразования строк с помощью метода
- 125. 1. Линейное программирование. 1.16. Модифицированный симплекс-метод Рассмотрим пример решения задачи ЛП (Х.А.Таха): максимизировать F=x1+4x2+7x3+5x4 при ограничениях:
- 126. 1. Линейное программирование. 1.16. Модифицированный симплекс-метод B=(P1,P2), то есть xB=(x1,x2)T и CB=(1,4)
- 127. 1. Линейное программирование. 1.16. Модифицированный симплекс-метод Так как целевая функция максимизируется, наличие отрицательного коэффициента при 4-й
- 128. 1. Линейное программирование. 1.16. Модифицированный симплекс-метод Найдем исключаемую переменную. Для нахождения выражения вычисляем вектор B-1P4 имеет
- 129. 1. Линейное программирование. 1.16. Модифицированный симплекс-метод Итак, в базисе B вектор P1 будет заменен на P2,
- 130. -
- 132. Скачать презентацию












































































 Русская литература 19 века в контексте мировой культуры
Русская литература 19 века в контексте мировой культуры YUFKIN FILMS Представляют Дерьмо,дерьмо, дерьмо Плачу 50 долларов.
YUFKIN FILMS Представляют Дерьмо,дерьмо, дерьмо Плачу 50 долларов. Преобразование двойных радикалов
Преобразование двойных радикалов От Петра І к Екатерине ІІ
От Петра І к Екатерине ІІ Презентация на тему История герба России
Презентация на тему История герба России Виды групповой работы и организация контроля учебной деятельности учащихся на уроке
Виды групповой работы и организация контроля учебной деятельности учащихся на уроке Стокгольмский синдром
Стокгольмский синдром Презентация на тему Островский "Гроза"
Презентация на тему Островский "Гроза" Сибирь
Сибирь Мы против терроризма
Мы против терроризма Пр4_Мод_Сист_Монга
Пр4_Мод_Сист_Монга 1663173619466__7x1efx (2)
1663173619466__7x1efx (2) Древняя и античная химия
Древняя и античная химия Финансовая система страны, ее сферы и звенья
Финансовая система страны, ее сферы и звенья Домашнее задание
Домашнее задание Презентация на тему Чудесные превращения воды в природе
Презентация на тему Чудесные превращения воды в природе  Походный мольберт, палитра, автомат
Походный мольберт, палитра, автомат Презентация Microsoft PowerPoint [Автосохраненный]
Презентация Microsoft PowerPoint [Автосохраненный] СП лекция-04ua
СП лекция-04ua Документальный фильм Аполлон-11
Документальный фильм Аполлон-11 Процессуальное право. Гражданский и арбитражный процесс
Процессуальное право. Гражданский и арбитражный процесс Анализ урока – один из главных инструментов управления качеством преподавания в школе
Анализ урока – один из главных инструментов управления качеством преподавания в школе Профилактика правонарушений. Профилактика вредных привычек
Профилактика правонарушений. Профилактика вредных привычек Презентация на тему Страницы истории Великой Отечественной войны
Презентация на тему Страницы истории Великой Отечественной войны внутриутробное развитие плода
внутриутробное развитие плода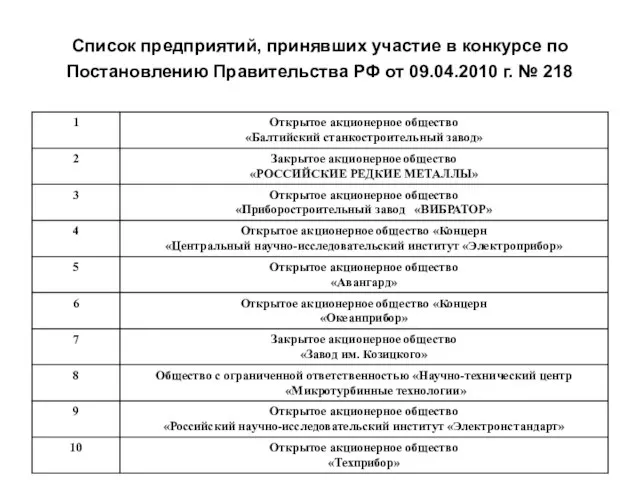 Список предприятий, принявших участие в конкурсе по Постановлению Правительства РФ от 09.04.2010 г. № 218
Список предприятий, принявших участие в конкурсе по Постановлению Правительства РФ от 09.04.2010 г. № 218 Авторское и смежное право
Авторское и смежное право Техника выполнения стойки на голове
Техника выполнения стойки на голове