Содержание
- 2. Тема Выборочное наблюдение Общая теория статистики
- 3. http://oknedis.narod.ru/ Контактный телефон моб. 8(925)502-36-48 Анатолий Викторович Интернет помощь
- 4. План 1.Определение выборочного наблюдения 2. Виды и схемы отбора 3.Характеристики генеральной и выборочной совокупности 4. Ошибка
- 5. 1.Определение выборочного наблюдения Выборочное наблюдение — это способ несплошного статистического наблюдения, при котором обследуются не все
- 6. Под выборочным методом понимается обследование части совокупности (выборочной совокупности), после чего, на основании полученных результатов, делаются
- 7. 1.Определение выборочного наблюдения Из генеральной совокупности отбирается часть единиц. По ним проводится исследование, а затем результаты
- 8. Причины применения: ♦ Экономия ♦ Невозможность проведения сплошного исследования
- 9. Основные обозначения N – объем, численность, число единиц ГС n – объем ВС
- 10. Основная идея выборочного метода состоит в том, что в результате обследования части совокупности можно судить с
- 11. Для того, чтобы выборочная совокупность давала объективные результаты, она должна быть репрезентативной (каждая единица генеральной совокупности
- 12. Основной предпосылкой применения выборочного метода является обеспечение равной возможности каждой единице генеральной совокупности попасть в выборку.
- 13. Теоретической основой выборки являются теоремы закона больших чисел (Чебышева, Ляпунова, Бернулли и др.)
- 14. Теоремы Чебышева, Ляпунова и закон больших чисел доказывают сходство генеральной ГС и выборочных ВС совокупностей. Различия
- 15. Задачи выборочного метода ♦ Определение доверительного интервала, в котором находится характеристика генеральной совокупности ♦ Определение минимального
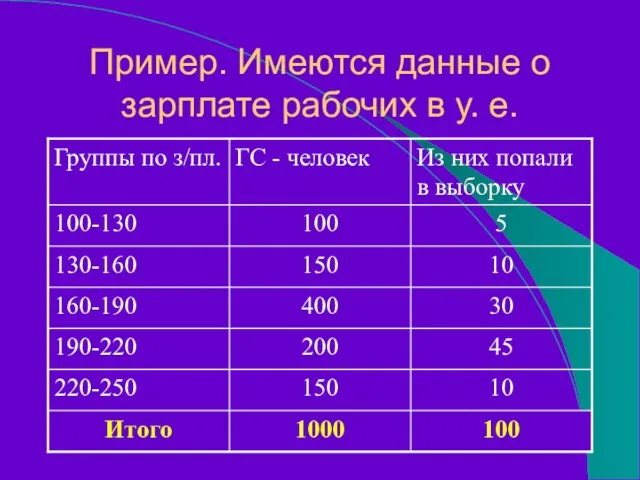
- 16. Пример. Имеются данные о зарплате рабочих в у. е.
- 17. 1.Определение выборочного наблюдения Как видим, зарплату от 100 до 130 в ГС получают 10%, в ВС
- 18. Сходство ГС и ВС Из теорем Чебышева, Ляпунова и закона больших чисел следует: 1-Хотя каждая выборочная
- 19. 1.Определение выборочного наблюдения Реально наблюдаемая совокупность объектов, статистически представленная рядом наблюдений x1, x2,…, xn случайной величины
- 20. Основные обозначения: N – объем генеральной совокупности (количество единиц генеральной совокупности). n – объем выборочной совокупности
- 21. В основе решения задач на выборочный метод лежат формулы предельных ошибок выборки
- 22. Обозначения t - число, связанное с вероятностью через табл. закона нормального распределения - средняя ошибка выборки
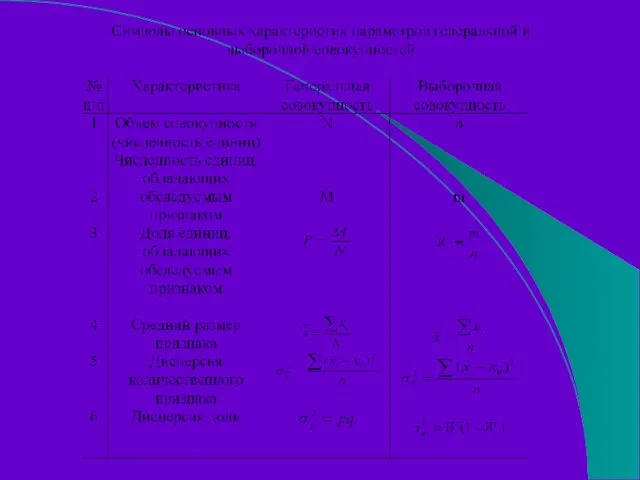
- 23. Ошибки выборки - генеральная средняя - генеральная доля - ошибка средней - ошибка доли
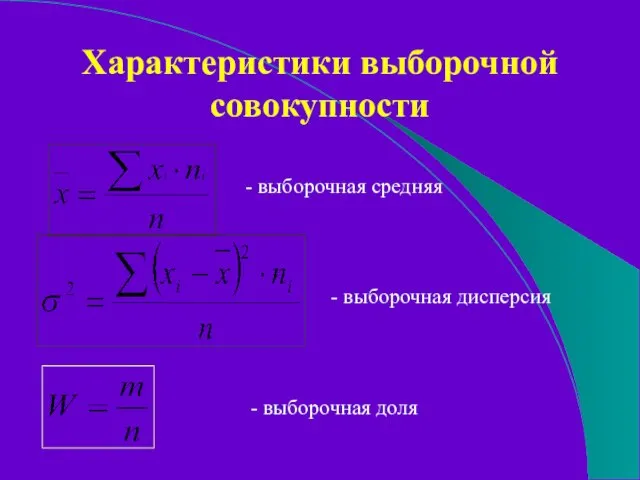
- 24. Характеристики выборочной совокупности - выборочная средняя - выборочная дисперсия - выборочная доля
- 25. 1.1. Объем выборки Число наблюдений n, образующих выборку, называется объемом выборки. Если объем выборки n достаточно
- 26. Малая выборка
- 27. Малой считается выборка, в которую входит меньше 20 единиц.
- 28. Рассмотрим особенности малой выборки. 1) Если мы работаем с обычной выборкой, то используется таблица «Интеграла вероятностей
- 29. 2) При малой выборке из формул исключается т. е. получается: ∆м.в. = 2
- 30. 1.1. Объем выборки Выборка считается малой, если при измерении одномерной случайной величины X объем выборки не
- 31. 1.2. Вариационный ряд Выборка образует вариационный ряд, если ее члены являются порядковыми статистиками, т. е. выборочные
- 32. 1.3.Условия проведения выборки Выборка будет представлять всю совокупность с приемлемой точностью при выполнении двух условий.
- 33. 1.3.Условия проведения выборки Во-первых, она должна быть достаточно многочисленной, чтобы в ней могли проявиться закономерности, существующие
- 34. 1.3.Условия проведения выборки Во-вторых, элементы выборки должны быть отобраны объективно, независимо от воли исследователя, чтобы каждый
- 35. 1.Определение выборочного наблюдения Генеральная совокупность может быть конечной (число наблюдений N = const) или бесконечной (N
- 36. 1.Определение выборочного наблюдения Одна и та же случайно отобранная совокупность объектов – парикмахерских одного административного округа
- 37. Способы отбора По виду различают индивидуальный, групповой и комбинированный отбор. При индивидуальном отборе в выборочную совокупность
- 38. 2.Виды и схемы отбора Процесс образования выборочной совокупности называется отбором. Он осуществляется в порядке беспристрастного, случайного
- 39. 1. Простой случайный отбор при котором n объектов случайно извлекаются из генеральной совокупности N объектов (например
- 40. Случайная выборка ♦ Случайная выборка - основа всех других способов отбора. ♦ Случайная выборка осуществляется методом
- 41. Пример 1. •Нужно отобрать 50 единиц из 500 (десятипроцентная выборка) • 4 781 • 3 215
- 42. Формулы предельных ошибок выборки
- 43. Обозначения: • - выборочная дисперсия; • W - выборочная доля; • n - объем выборочной совокупности;
- 44. Пример 2. Для определения среднего срока службы изделий было обследовано 250 изделий. При этом средний срок
- 45. Решение: • Р=0,9973, t=3 (из таблицы интеграла вероятностей закона нормального распределения). • При этом вероятность делится
- 46. Пример 3. • Определить вероятность того, что предельная ошибка средней службы не превысит 1 месяц. Решение:
- 47. Пример 4. Определение минимального объема выборки. Сколько следует прохронометрировать операций, чтобы с вероятностью 0,9973 можно было
- 48. Решение : Ответ: нужно прохронометрировать не менее 441 операции.
- 49. 2. Простой отбор с помощью регулярной процедуры осуществляется с применением механической составляющей (номера квартиры, даты, дня
- 50. 3. Стратифицированный отбор заключается в том, что генеральная совокупность объема N подразделяется на части совокупности или
- 51. 3. Стратифицированный отбор Страты - однородные объекты с точки зрения статистических характеристик (например, население по возрасту
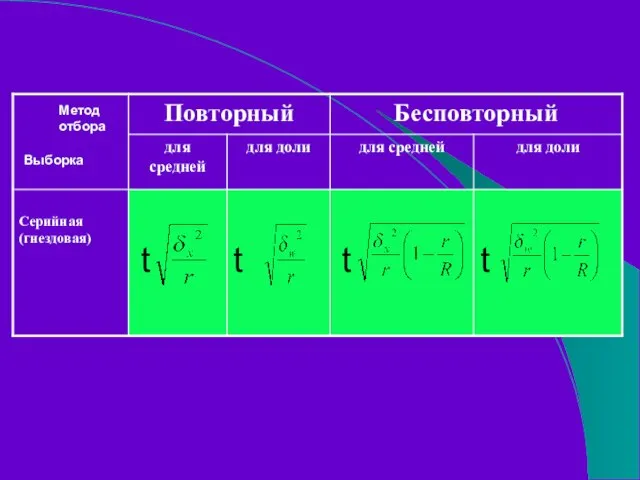
- 52. 4.Серийный отбор Приемы серийного отбора используются для формирования серийных или гнездовых выборок. Они удобны в том
- 53. Вся совокупность делится на серии, после чего механическим или собственно случайным способом отбирается некоторое количество серий.
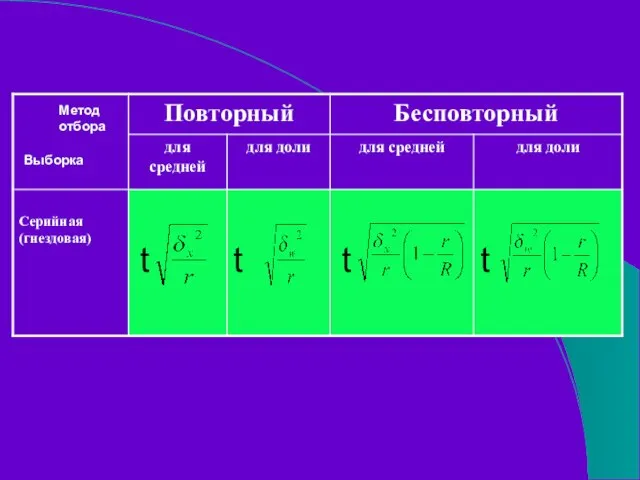
- 54. t t t t Метод отбора Выборка
- 55. r – количество отобранных серий R – общее число серий - межсерийная дисперсия - межсерийная выборочная
- 56. Пример: На предприятии 10 бригад. Изучается производительность труда. Отбираются 2 бригады. Средняя производительность труда 1-й бригады
- 57. ОТВЕТ:
- 58. Типическая выборка
- 59. Типическая выборка способ проведения типической выборки: 1. вся совокупность делится на типические группы население сельское городское
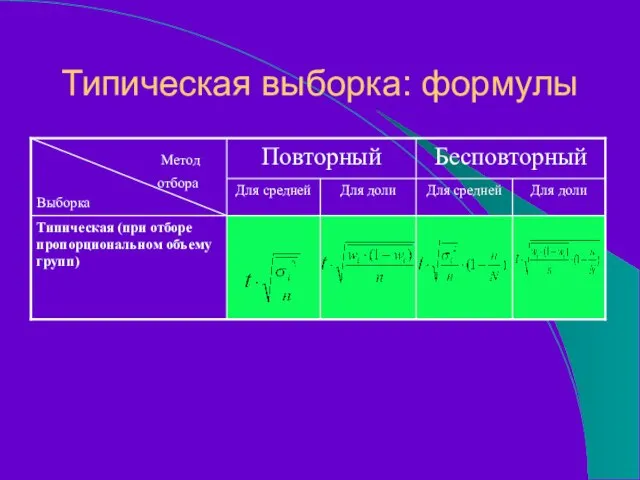
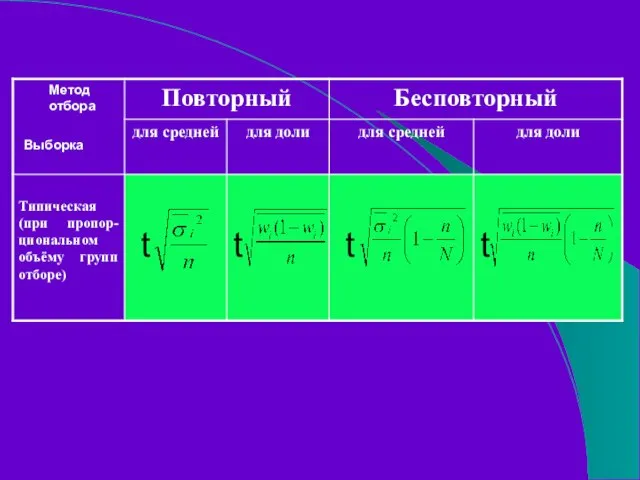
- 60. Объем выборки При отборе, пропорциональном объему типических групп, число наблюдений по каждой группе определяется по формуле:
- 61. Типическая выборка: формулы
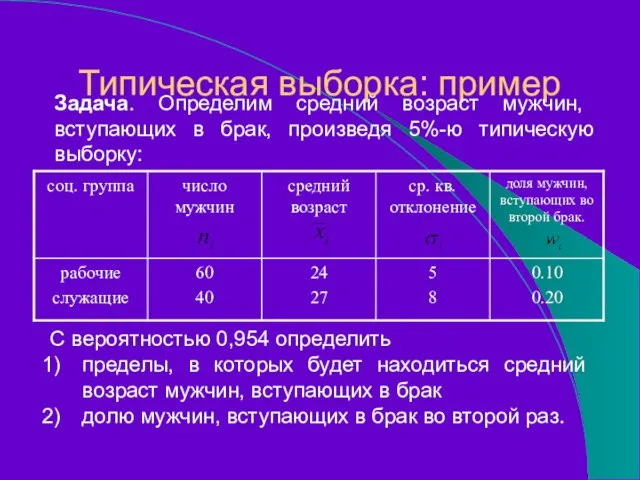
- 62. Типическая выборка: пример Задача. Определим средний возраст мужчин, вступающих в брак, произведя 5%-ю типическую выборку: С
- 63. Типическая выборка: пример Решение. 1) Средний возраст вступления в брак мужчин находится в пределах
- 64. Таким образом, с вероятностью 0,954 можно утвердить, что средний возраст мужчин, вступающих в брак, принимает значения
- 65. Типическая выборка: пример Решение. 2) Доля мужчин, вступающих в брак во второй раз, находится в пределах
- 66. Таким образом, с вероятностью 0,954 можно утверждать, что доля мужчин, вступающих в брак во второй раз,
- 67. 5. Комбинированный (ступенчатый ) отбор может сочетать в себе сразу несколько способов отбора (например, стратифицированный и
- 68. 2.1.Виды отбора По виду различаются индивидуальный, групповой и комбинированный отбор. При индивидуальном отборе в выборочную совокупность
- 69. 2.2. Методы отбора По методу отбора различают повторную и бесповторную выборку. Бесповторным называется отбор, при котором
- 70. При повторном отборе попавшая в выборку единица после регистрации возвращается в генеральную совокупность и таким образом
- 71. Механическая выборка При механической выборке вся совокупность делится на группы по числу единиц, которые должны войти
- 72. Механическая выборка. • При механической выборке вся совокупность разбивается на столько групп, сколько единиц должно войти
- 74. На практике механическая выборка обычно осуществляется при помощи так называемого шага отбора 1) Все единицы совокупности
- 75. 3.Характеристики генеральной и выборочной совокупности В основе статистических выводов проведенного исследования лежит распределение случайной величины Х,
- 76. 3.Характеристики генеральной и выборочной совокупности Распределение случайной величины Х в генеральной совокупности носит теоретический, идеальный характер,
- 77. 3.Характеристики генеральной и выборочной совокупности Некоторые теоретические распределения заданы аналитически, т.е. их параметры определяют значение функции
- 78. 3.Характеристики генеральной и выборочной совокупности Для выборки же функцию распределения определить трудно, а иногда невозможно, поэтому
- 79. 3.1. Нормальное распределение По своей природе распределения бывают непрерывными и дискретными. Наиболее известным непрерывным распределением является
- 80. 3.Характеристики генеральной и выборочной совокупности Среди дискретных в социально-экономических исследованиях наиболее часто применяется альтернативное (дихотомическое) распределение.
- 81. 3.2. Альтернативное (дихотомическое) распределение . Параметр математического ожидания μ этого распределения выражает относительную величину (или долю)
- 82. 3.Характеристики генеральной и выборочной совокупности В зависимости от вида распределения и от способа отбора единиц совокупности
- 83. 3.3.Доля выборки Долей выборки kn называется отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности:
- 84. 3.4.Выборочная доля Отношение числа единиц, обладающих данным признаком или данным его значением m, к общему числу
- 85. Пример В партии товара, содержащей 10 тыс. штук, при 4% выборке доля выборки kn в абсолютной
- 86. -генеральная доля W – выборочная доля
- 88. 4.Ошибка выборочного наблюдения Поскольку выборочная совокупность отлична от генеральной, то возникают ошибки выборки. При сплошном и
- 89. 4.Ошибка выборочного наблюдения Ошибки регистрации могут иметь случайный и систематический характер. Случайные ошибки складываются из множества
- 90. 4.Ошибка выборочного наблюдения Систематические ошибки тенденциозны, так как нарушают правила отбора объектов в выборку (например, отклонения
- 91. 4.Ошибка выборочного наблюдения Ошибки репрезентативности присущи только выборочному наблюдению. Их невозможно избежать, поскольку выборочная совокупность не
- 92. 4.Ошибка выборочного наблюдения Ошибка выборочного наблюдения ε есть разность между значением параметра в генеральной совокупности и
- 93. – генеральная доля W – выборочная доля – число единиц, обладающих признаком в генеральной совокупности
- 95. Ошибка выборки – это разность между характеристиками выборочной и генеральной совокупности. - ошибка средней - ошибка
- 96. - генеральная средняя (средняя величина, которая имеет место в генеральной совокупности) - выборочная средняя где -
- 97. 4.Ошибка выборочного наблюдения Ошибки выборки свойственны только выборочным наблюдениям. Чем больше эти ошибки, тем больше эмпирическое
- 98. Ошибка выборки – это разность между характеристиками выборочной и генеральной совокупности. - ошибка средней - ошибка
- 99. Теоремы закона больших чисел устанавливают связь между предельной ошибкой выборки, гарантированной с определенной вероятностью, числом (
- 102. Теорема Ляпунова А.М. Ляпунов доказал, что распределение выборочных средних( а следовательно, и их отклонений от генеральной
- 103. Теорема Ляпунова Математически теорему Ляпунова можно записать так: где π=3,14(математическая постоянная); - предельная ошибка выборки, которая
- 106. 4.Ошибка выборочного наблюдения Параметры эмпирического распределения x и s2 являются случайными величинами, следовательно, ошибки выборки также
- 107. Средняя ошибка выборки m =
- 108. Средняя ошибка выборки выражает среднее квадратическое отклонение выборочной средней от математического ожидания. Эта величина при соблюдении
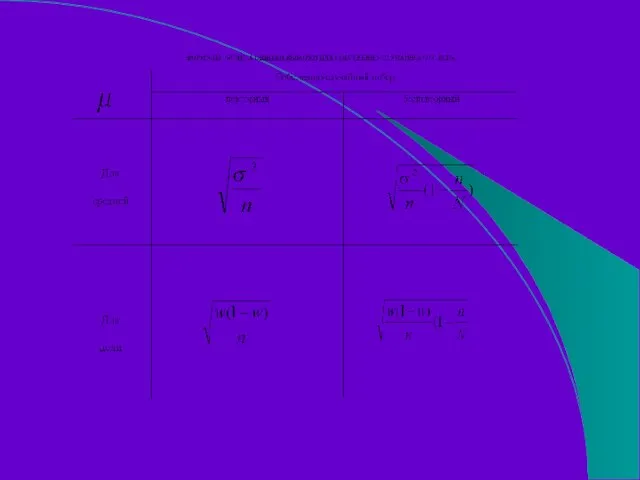
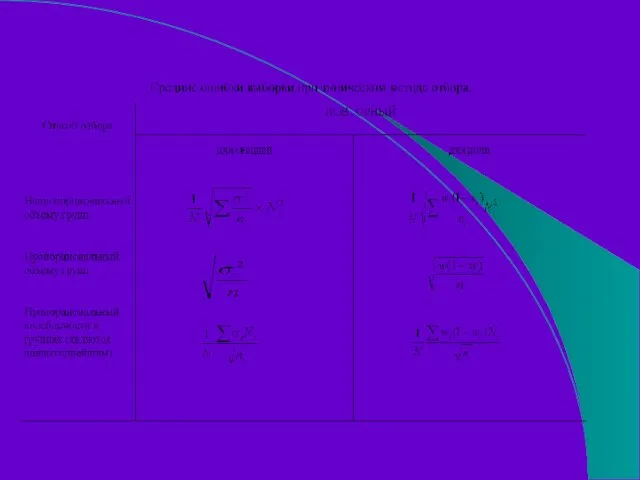
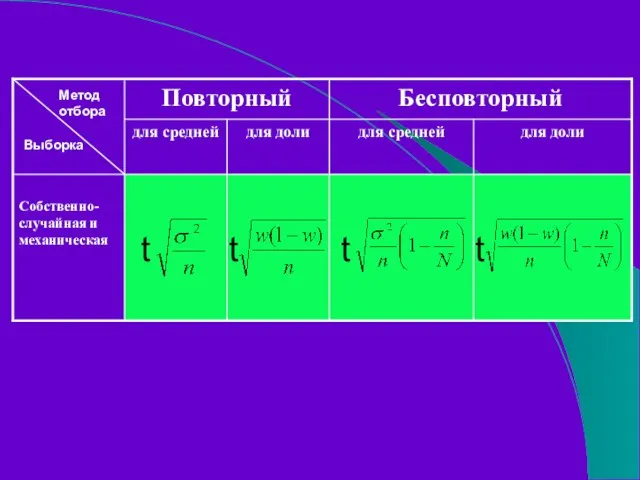
- 112. Предельная ошибка выборки для некоторых способов формирования выборочной совокупности
- 113. t t t t Метод отбора Выборка
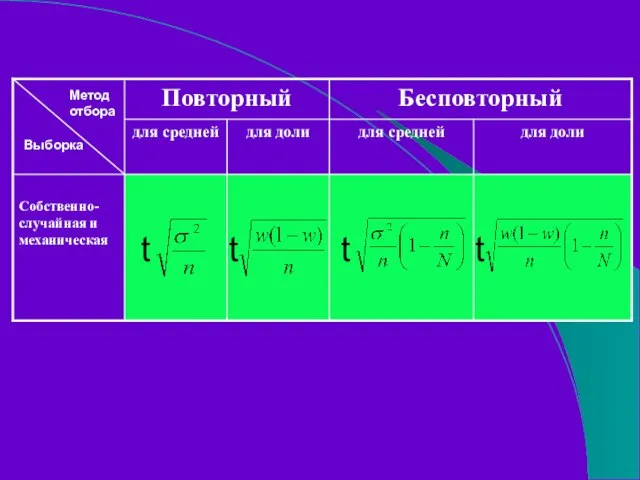
- 114. t t t t Метод отбора Выборка
- 115. t t t t Метод отбора Выборка
- 116. t t t t Метод отбора Выборка
- 117. 6. Необходимый объем выборки
- 120. Задача В городе 2000 семей. Предполагается провести выборочное обследование методом случайной бесповторной выборки для нахождения среднего
- 121. Определить необходимую численность выборки при условии, что с вероятностью 0,954 ошибка выборки не превысит 1 человека
- 122. Формула
- 123. Решение
- 124. Исходные данные данные
- 125. Ответ Необходимо обследовать не менее 36 семей.
- 127. Скачать презентацию
















































































































 Евангелие, которое мы проповедуем
Евангелие, которое мы проповедуем Введение. Основы безопасности жизнедеятельности
Введение. Основы безопасности жизнедеятельности СТОП вырубке ёлок!
СТОП вырубке ёлок! Тарифы курса Убеждения на миллион
Тарифы курса Убеждения на миллион Institute for Materials Science Problems n. I.N.Frantsevich NAN of the UkraineDiamond -hardalloy macrocomposit high-modulus material brand AVKM
Institute for Materials Science Problems n. I.N.Frantsevich NAN of the UkraineDiamond -hardalloy macrocomposit high-modulus material brand AVKM Поздравление от 5 «А»
Поздравление от 5 «А» Автомобили Франции
Автомобили Франции  Родительское собрание ТЕМА: «Служба школьной медиации»
Родительское собрание ТЕМА: «Служба школьной медиации» ЗИЛ-4421 1994г.в., дв. ЯМЗ-236 Полуприцеп ОДАЗ-885, 1980 г.в. УТС, цена 150 000 р. Торг. г. Барабинск, ул. Коммунистическая - 1 Т. (383) 289-25-23.
ЗИЛ-4421 1994г.в., дв. ЯМЗ-236 Полуприцеп ОДАЗ-885, 1980 г.в. УТС, цена 150 000 р. Торг. г. Барабинск, ул. Коммунистическая - 1 Т. (383) 289-25-23. Проект о скидках в процентах под Новый Год на Сотовую связь
Проект о скидках в процентах под Новый Год на Сотовую связь Правописание приставок
Правописание приставок ПРОБЛЕМА ВНЕДРЕНИЯ СТАНДАРТОВ ВТОРОГО ПОКОЛЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫЕ ШКОЛЫ
ПРОБЛЕМА ВНЕДРЕНИЯ СТАНДАРТОВ ВТОРОГО ПОКОЛЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫЕ ШКОЛЫ Географическая оболочка
Географическая оболочка Kursus «Tehniline analuus»maht: 1 ON
Kursus «Tehniline analuus»maht: 1 ON Конкурс ведущих
Конкурс ведущих The Finest of Fine Teas
The Finest of Fine Teas Тепловые насосы BROS
Тепловые насосы BROS Презентация на тему Принципы гражданского и арбитражного процесса
Презентация на тему Принципы гражданского и арбитражного процесса План развития сетей на 2018-2019 г
План развития сетей на 2018-2019 г Презентация на тему Дикие и домашние животные (3 класс)
Презентация на тему Дикие и домашние животные (3 класс) Презентация на тему Основные понятия компьютерной графики
Презентация на тему Основные понятия компьютерной графики  проф. С.В. Шалаев
проф. С.В. Шалаев 1. АПС 2020
1. АПС 2020 СТАТИСТИКА ЭНЕРГЕТИКИ УКРАИНЫ: ГАЗ ПРИРОДНЫЙ Баку, Азербайджан 27-28 сентября 2011 Анатолий Фризоренко Директор департамента ст
СТАТИСТИКА ЭНЕРГЕТИКИ УКРАИНЫ: ГАЗ ПРИРОДНЫЙ Баку, Азербайджан 27-28 сентября 2011 Анатолий Фризоренко Директор департамента ст Государственно-политическое развитие Великобритании в 17-19 вв. Становление в Англии конституционной монархии
Государственно-политическое развитие Великобритании в 17-19 вв. Становление в Англии конституционной монархии Запас вооруженных сил РФ
Запас вооруженных сил РФ Псевдо-конфликт. Факт-конфликт. Эго-конфликт
Псевдо-конфликт. Факт-конфликт. Эго-конфликт Felting exhibition(выставка из фетровых изделий)
Felting exhibition(выставка из фетровых изделий)