Содержание
- 2. Задачи урока: актуализировать и углубить знания, полученные ранее по данному разделу; вспомнить определение логики, понятия, высказывания,
- 3. «….по одной капле воды… человек, умеющий мыслить логически, может сделать вывод о существовании Атлантического океана или
- 4. Задача Иван против Кащея бессмертного Темница I – «Здесь Василиса Прекрасная». Темница II – « Темница
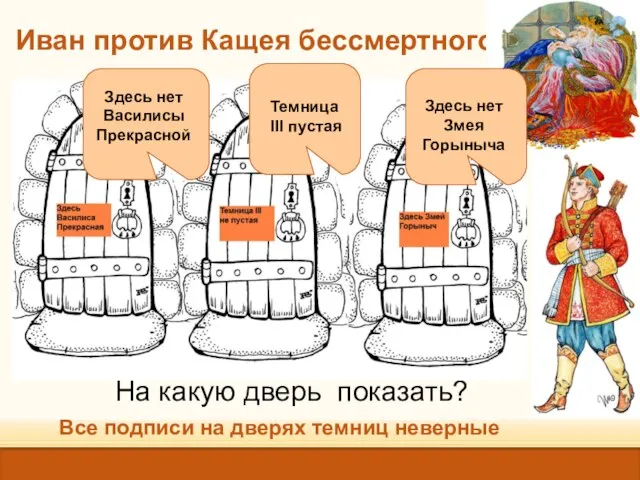
- 5. Иван против Кащея бессмертного Все подписи на дверях темниц неверные На какую дверь показать? Здесь нет
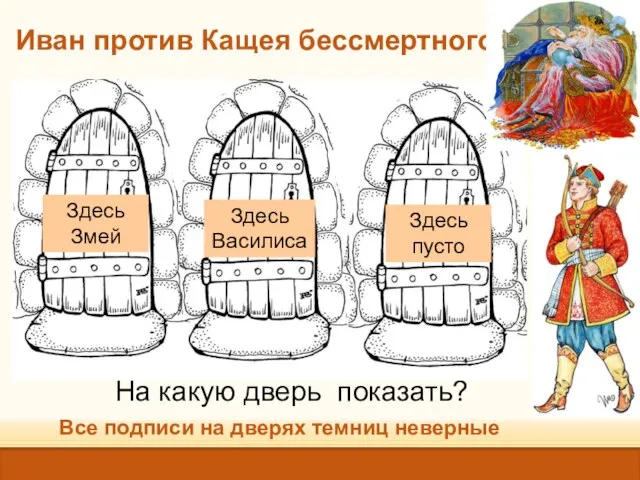
- 6. Иван против Кащея бессмертного Все подписи на дверях темниц неверные На какую дверь показать? Здесь Змей
- 7. Где же правда? Дядюшка Скрудж попал на остров. На нем живут только правдолюбы (они всегда говорят
- 8. Решение Если лгун, значит соврал Лгун Если правдолюб, значит сказал правду Правдолюб В обоих случаях ответ
- 9. Задача «Уроки логики» Если изучал первый, то изучал и второй, но неверно, что если изучал третий,
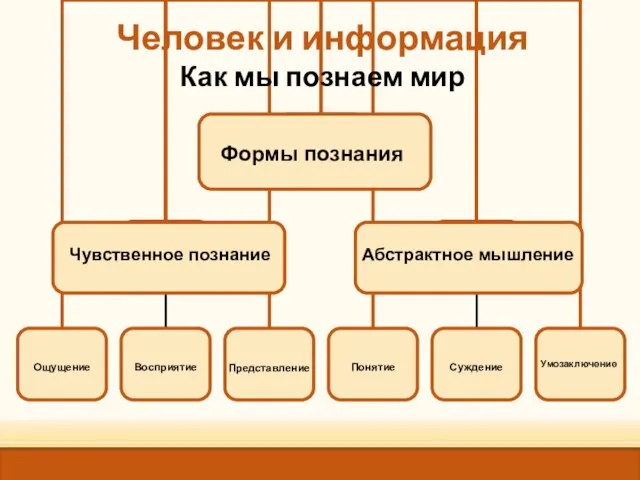
- 10. Представление Умозаключение Формы познания Чувственное познание Абстрактное мышление Человек и информация Как мы познаем мир
- 11. Решите кроссворд «Если у двух человек есть по одному яблоку и они обмениваются ими, у каждого
- 12. Кроссворд Мысль, в которой что-либо утверждается или отрицается. Мысленное соединение в единое целое частей объекта или
- 13. Пингвины – чёрно-белые. Старые фильмы тоже черно-белые. Поэтому пингвины – это старые фильмы. В V до
- 14. Математические софизмы 4 = 5 16 - 36 = 25 – 45 (4 - )2= (5
- 15. Математические софизмы 4 = 5
- 16. Математические софизмы
- 17. Математические софизмы Дополнительное задание 5 = 1 Из числа 5 и 1 по отдельности вычтем одно
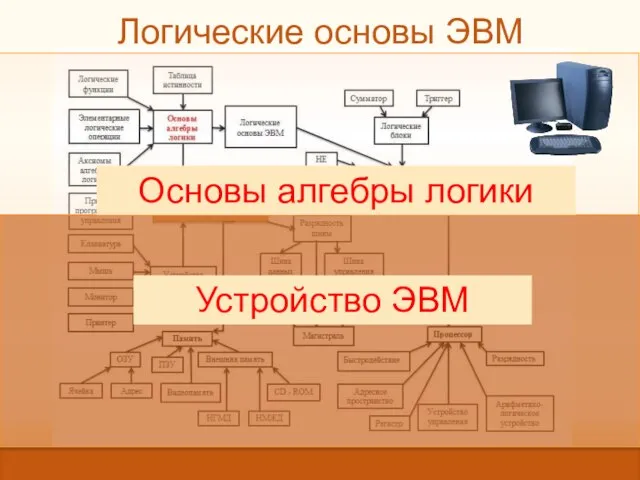
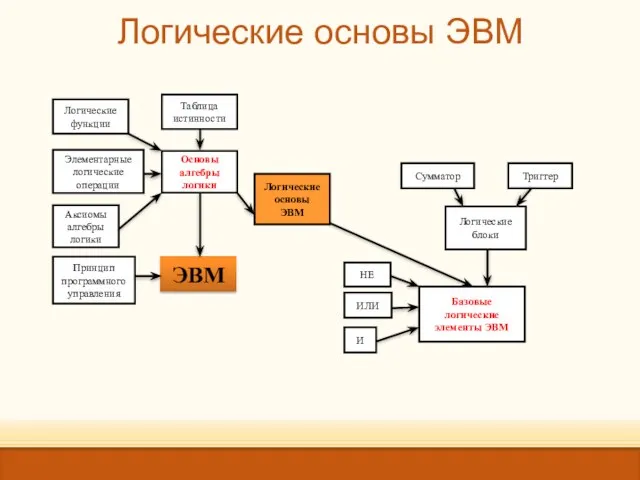
- 18. Логические основы ЭВМ Устройство ЭВМ Основы алгебры логики
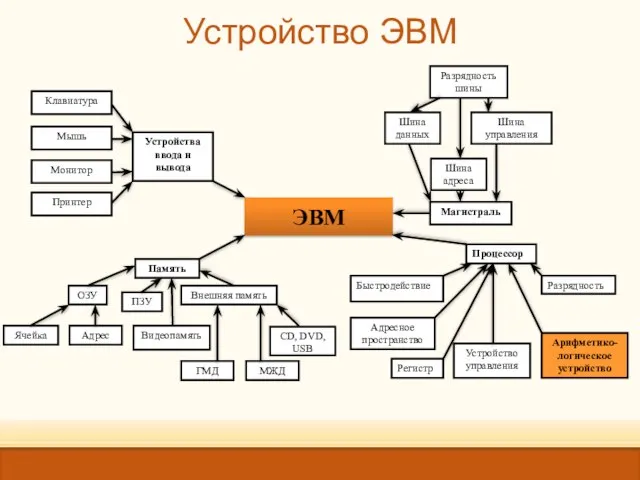
- 19. Устройство ЭВМ ЭВМ
- 20. Логические основы ЭВМ
- 21. На уроках алгебры Алгебра в широком смысле этого слова – наука об общих операциях, аналогичных сложению
- 22. На уроках алгебры Неравенство вида f(IxI) Система соответствует логической связке «И». Совокупность соответствует логической связке «ИЛИ».
- 23. Практическая работа «То, чем в прежние эпохи занимались лишь зрелые умы ученых мужей, в более поздние
- 24. Заполните таблицу
- 25. Домашнее задание 1. Учебник стр.96-99 Творческое задание Опираясь на созданную таблицу, подготовить презентацию «Этапы развития логики
- 27. Скачать презентацию


















 Современные возможности пробиотической терапии в клинике внутренних болезней
Современные возможности пробиотической терапии в клинике внутренних болезней Территория смыслов
Территория смыслов Карта пробных ароматов: Al Haramain/Aysha (милая)
Карта пробных ароматов: Al Haramain/Aysha (милая) Понятие мониторинга
Понятие мониторинга Прием письменного вычитания в случаях вида 50-24
Прием письменного вычитания в случаях вида 50-24 Акварельные зарисовки
Акварельные зарисовки Русские народные сказки
Русские народные сказки Красная книга растений
Красная книга растений Биография. Шаблон
Биография. Шаблон Дифференциальная диагностика и принципы лечения синдрома Корнелии Де ЛАНГЕ
Дифференциальная диагностика и принципы лечения синдрома Корнелии Де ЛАНГЕ Презентация на тему Телескоп
Презентация на тему Телескоп Презентация Сушильникова Н.И. Экологическая сказка
Презентация Сушильникова Н.И. Экологическая сказка Телеметрическая платформа M2MGate Solution
Телеметрическая платформа M2MGate Solution Китайский клуб МИИТа
Китайский клуб МИИТа Тема выпускной квалификационной работы. Шаблон
Тема выпускной квалификационной работы. Шаблон Морской порт Санкт-Петербург. Отчет по результатам линейного обхода
Морской порт Санкт-Петербург. Отчет по результатам линейного обхода С днем рождения!!!
С днем рождения!!! Муниципальное дошкольное образовательное учреждение «Детский сад № 15» г. Чебоксары
Муниципальное дошкольное образовательное учреждение «Детский сад № 15» г. Чебоксары Презентация на тему Климат Африки
Презентация на тему Климат Африки Коммуникативный практикум
Коммуникативный практикум Государство. Понятие. Теории происхождения
Государство. Понятие. Теории происхождения Жизнь прекрасна
Жизнь прекрасна Измерение расхода. FR — лидер в новейшей высокоточной технологии измерения расхода
Измерение расхода. FR — лидер в новейшей высокоточной технологии измерения расхода Венев
Венев ПУТЕШЕСТВИЕ ПО МАТЕРИКАМ
ПУТЕШЕСТВИЕ ПО МАТЕРИКАМ Экономия водоснабжения
Экономия водоснабжения Рифмоплёт
Рифмоплёт Вареники с картошкой
Вареники с картошкой