Задача Коши

Введение
Математическое моделирование – это технология изучения и прогнозирования проявлений интересующих нас объектов с использованием возможностей математики.

Введение
Математическая модель - это приближенное представление закономерности проявления некоторого класса объектов или явлений окружающего мира, выраженное в виде математических конструкций–аналогов и сформулированное в математических терминах и символах.

Введение
Этапы решения задачи математического моделирования:
1) Построение математической модели.
2) Исследование задачи на основе построенной модели.
3) Оценка адекватности модели и внесение корректив.
4) Возможное совершенствование модели.

Введение
Моделирование и компьютер:
Процедуру математического моделирования все чаще неразрывно связывают с использованием компьютеров. В современных информационных технологиях математическое моделирование играет роль «интеллектуального ядра» - наукоемкого фильтра, преобразующего «информационное сырье в готовый продукт, т.е. в точное знание».

Введение в задачу Коши
Задача Коши — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).

Введение в задачу Коши
Основные вопросы, которые связаны с задачей Коши, таковы:
1)Существует ли (хотя бы локально) решение задачи Коши?
2)Если решение существует, то какова область его существования?
3)Является ли решение единственным?
4)Если решение единственно, то будет ли оно корректным, то есть непрерывным (в каком-либо смысле) относительно начальных данных?

Введение в задачу Коши
Различные постановки задачи Коши:
1) ДУ первого порядка, разрешённое относительно производной.
2) Система n ДУ первого порядка, разрешённая относительно старших производных.
3) ДУ n-го порядка, разрешённое относительно старшей производной.

Теоремы о разрешимости задачи Коши для ДУ
Пусть в области рассматривается задача Коши:
где . Пусть правая часть является непрерывной функцией в . В этих предположениях имеет место теорема Пеано, устанавливающая локальную разрешимость задачи Коши.

Теоремы о разрешимости задачи Коши для ДУ
Чтобы сформулировать теорему о единственности решения задачи Коши, необходимо наложить дополнительные ограничения на правую часть. Введем константу L, такую что
Тогда если L существует, то функция f(x,y) удовлетворяет условию Липшица на D относительно y и следовательно задача Коши не может иметь в D более одного решения.

Теоремы о разрешимости задачи Коши для ДУ
Для существования глобального решения необходимо наложить условия на рост правой части по y: пусть функция f удовлетворяет условию
где A>0 - константа не зависящая ни от x, ни от y, тогда задача Коши имеет решение в D.

Задача об изгибе балки
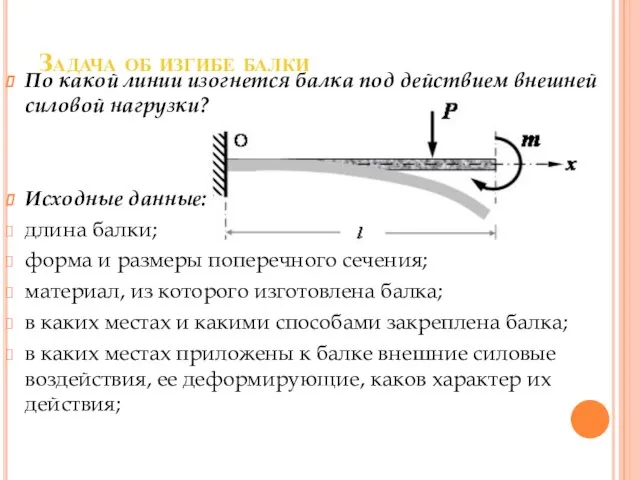
По какой линии изогнется балка под действием внешней силовой нагрузки?
Исходные данные:
длина балки;
форма и размеры поперечного сечения;
материал, из которого изготовлена балка;
в каких местах и какими способами закреплена балка;
в каких местах приложены к балке внешние силовые воздействия, ее деформирующие, каков характер их действия;

Задача об изгибе балки
Этап 1: Формулирование идеи, закладываемой в математическую модель.
Если внешняя силовая нагрузка, изогнув закрепленную балку, не меняясь, продолжает на нее действовать, изогнувшаяся балка остается в состоянии равновесия, примет состояние покоя.

Задача об изгибе балки
Этап 2: Формирование математической модели поставленной задачи.
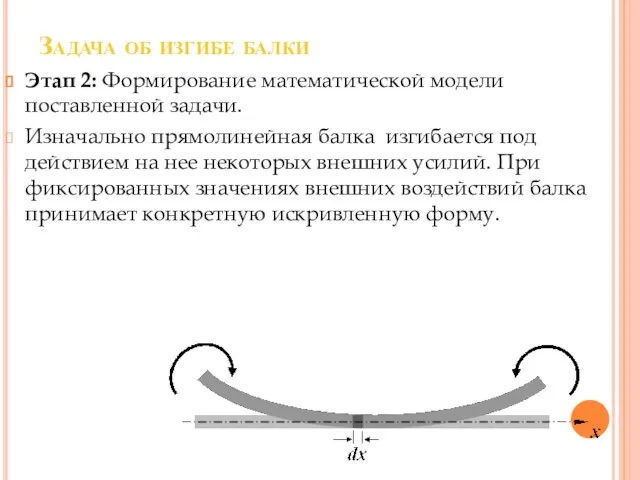
Изначально прямолинейная балка изгибается под действием на нее некоторых внешних усилий. При фиксированных значениях внешних воздействий балка принимает конкретную искривленную форму.

Задача об изгибе балки
Для упрощения модели введем гипотезу плоских сечений:
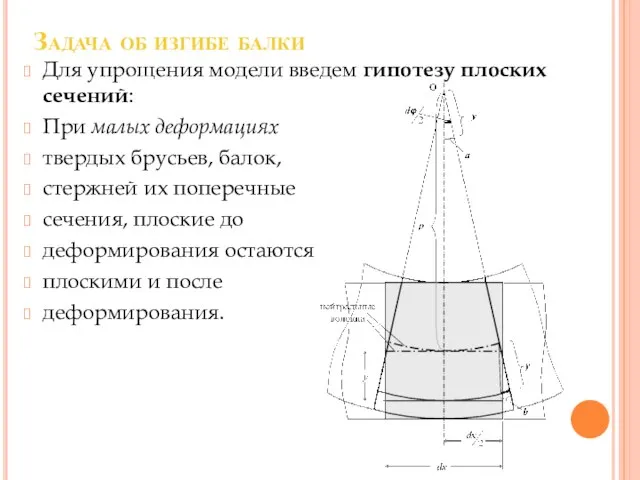
При малых деформациях
твердых брусьев, балок,
стержней их поперечные
сечения, плоские до
деформирования остаются
плоскими и после
деформирования.

Задача об изгибе балки
Если допускать, что длина дуги b равна длине дуги a, то относительную линейную деформацию волокон , вызванную изгибом балки, можно вычислить по упрощенной формуле:
Кривизна нейтральных волокон k изогнутой балки на ее предельно коротком фрагменте dx равна:
а в условиях гипотезы малости деформаций:
а так как , то

Задача об изгибе балки
Таким образом, линейная деформация волокон, расположенных на расстоянии y от нейтрального слоя в некотором ее сечении, может быть вычислена по формуле: .
Так как балки при их небольшом изгибе фактически не меняют своей толщины, то каждое продольное волокно предельно малой толщины находится в условиях «одноосного» растяжения-сжатия и для вычисления величины нормального напряжения в продольном волокне можно использовать закон Гука:

Задача об изгибе балки
Внутреннее продольное усилие вычисляется как сила, равнодействующая нормальному напряжению , распределенному по поперечному сечению этого волокна:
где dF – площадь поперечного сечения волокна.
Так как центр тяжести каждого сечения лежит на нулевой линии, то так как в нашей задаче нет нагрузки, которая растягивала или сжимала бы балку, то суммарное продольное внутреннее усилие
равно 0:

Запись математической модели
Итак, в любом сечении балки, т.е. при любом :

Запись математической модели
При малых деформациях, когда значения перемещений точек деформируемого элемента существенно малы по сравнению с его размерами, можно принять
И тогда наше уравнение сводится к приближенному уравнению оси изогнутого бруса.

Запись математической модели
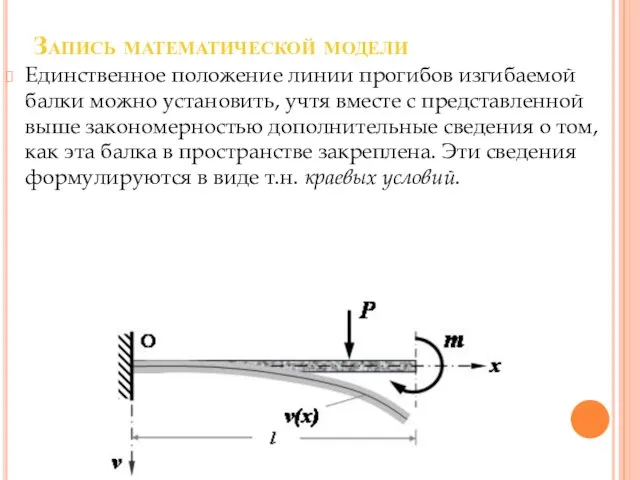
Единственное положение линии прогибов изгибаемой балки можно установить, учтя вместе с представленной выше закономерностью дополнительные сведения о том, как эта балка в пространстве закреплена. Эти сведения формулируются в виде т.н. краевых условий.

Запись математической модели
Для жестко закрепленной в левом торце консоли запись граничных условий принимает вид:
где – угол наклона оси изгибаемой балки.

Простейшая задача об изгибе консоли
Далее рассмотрим задачу об изгибе консоли под действием одной сосредоточенной поперечной внешней силы P.
Изгибающий момент, создаваемый внешней силой P в произвольном сечении K, может быть вычислен по формуле:
Эту формулу удобно переписать с участием функции Хевисайда:
где

Простейшая задача об изгибе консоли
Простейшей задачей об изгибе консоли является задача изгиба консоли под действием одной сосредоточенной поперечной внешней силы.
Математическая модель
для нее будет следующей:

Простейшая задача об изгибе консоли
Предложенную выше задачу можно решить аналитически, а можно при помощи метода конечных разностей. При решении методом конечных разностей мы заменим на f,
заменим на , на , после чего выразим и задача
преобразуется в следующую:

Простейшая задача об изгибе консоли
Зададим шаг разбиения h и, заменив производную на ее конечно-разностный аналог, будем рассматривать решение в точках с координатами :
Этим уравнениям соответствуют рекуррентные формулы пересчета по методу Эйлера:

Понятие об устойчивости разностной схемы
Рассмотрим простейшую задачу Коши вида:
где
В этом случае известно аналитическое решение
из которого видно, что
Разностная формула метода Эйлера имеет вид:
Из нее следует, что

Понятие об устойчивости разностной схемы
Обозначим тогда При этом очевидно, что только при что соответствует
Последнее неравенство называется условием устойчивости счета.

Пример
В качестве примера решим следующую задачу:

Пример
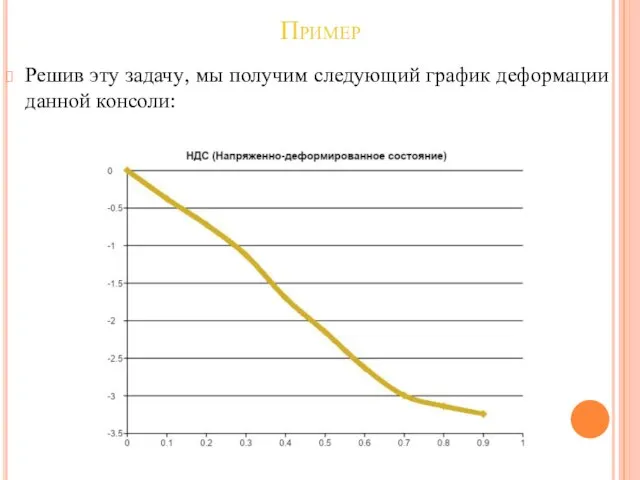
Решив эту задачу, мы получим следующий график деформации данной консоли: