Содержание
- 2. Задача Льва Толстого
- 3. 15 10 2 A D C B H 13 13 По теореме Пифагора Он путь нашел
- 4. Трапеция или прямоугольник ? выгадал он или прогадал от того, что участок его оказался не прямоугольником,
- 5. Трапеция или прямоугольник ? Следовательно, на вопрос задачи нельзя дать определенного ответа. Есть прямоугольники с большей
- 6. Замечательное свойство квадрата
- 7. Замечательное свойство квадрата
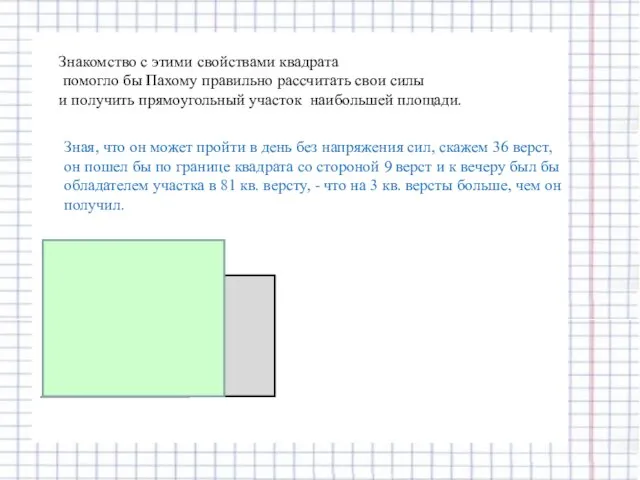
- 8. Знакомство с этими свойствами квадрата помогло бы Пахому правильно рассчитать свои силы и получить прямоугольный участок
- 9. Знакомство с этими свойствами квадрата помогло бы Пахому правильно рассчитать свои силы и получить прямоугольный участок
- 11. Мы сделали выводы Что из всех четырехугольников с одинаковым периметром наибольшую площадь имеет квадрат. 2. Из
- 12. Задачи, которые мы рассматривали, рассматривают вопрос со стороны как бы экономической: при данной затрате сил (например,
- 13. Произведение множителей, имеющих постоянную сумму Это произведение больше!
- 14. Мы рассмотрели и решили следующие задачи
- 15. 1. Доказать, что среди а) прямоугольников, б) ромбов с одинаковым периметром наибольшую площадь имеет квадрат. в)
- 16. А на последок… При помощи ножниц вырежьте в тетрадном листе дырку, через которую мог бы пролезть
- 17. Это всё, что мы хотели ВАМ сегодня рассказать ! Дальше есть решения задач. Можно посмотреть
- 18. Решение задач
- 19. Задача 1. Доказать, что среди а) прямоугольников, б) ромбов с одинаковым периметром наибольшую площадь имеет квадрат.
- 20. Задача 1. Доказать, что среди а) прямоугольников, б) ромбов с одинаковым периметром наибольшую площадь имеет квадрат.
- 21. Задача 1. Доказать, что среди а) прямоугольников, б) ромбов с одинаковым периметром наибольшую площадь имеет квадрат.
- 22. Из всех прямоугольников с заданным периметром, квадрат имеет наибольшую площадь (по теореме 1). Значит, прямоугольник должен
- 23. Из всех прямоугольников с заданным периметром, квадрат имеет наибольшую площадь (по теореме 1). Значит, прямоугольник должен
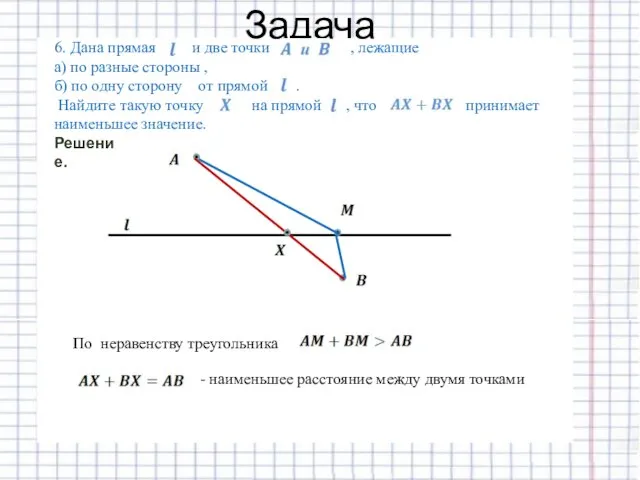
- 24. Задача Решение. По неравенству треугольника - наименьшее расстояние между двумя точками
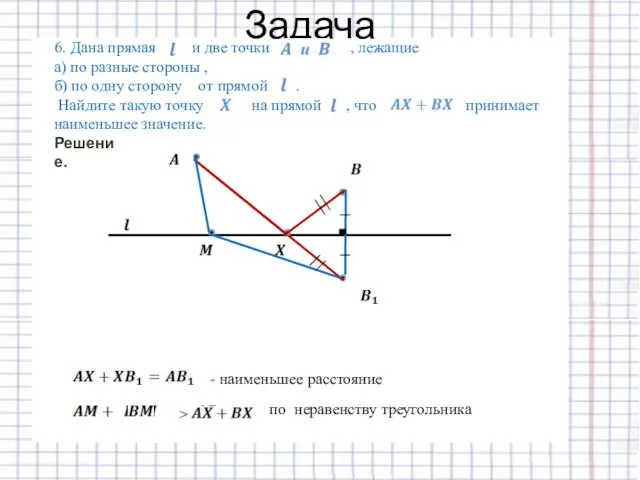
- 25. Задача Решение. по неравенству треугольника - наименьшее расстояние
- 26. Задача Решение.
- 29. Скачать презентацию























 Презентация на тему Культивирование клеток
Презентация на тему Культивирование клеток  День толерантности Мы разные, но мы вместе!
День толерантности Мы разные, но мы вместе! Художник Шишкин Иван Иванович. Картины о зиме
Художник Шишкин Иван Иванович. Картины о зиме Презентация на тему Лучший ученик
Презентация на тему Лучший ученик Философия_как_способ_духовного_познания
Философия_как_способ_духовного_познания Перспективы развития российской экономики в ближайшие годы
Перспективы развития российской экономики в ближайшие годы Christmas Traditions in Great Britain
Christmas Traditions in Great Britain 111
111 Презентация на тему Межличностные отношения
Презентация на тему Межличностные отношения Цепочки согласований
Цепочки согласований Храмы в искусстве
Храмы в искусстве Двунадесятые православные праздники
Двунадесятые православные праздники Кукла на Счастье
Кукла на Счастье Доходная недвижимость
Доходная недвижимость «Этот прекрасный, ужасный подросток!»
«Этот прекрасный, ужасный подросток!» MDM
MDM ВКР: Проектирование аппаратно-программных средств для диагностирования работы абонентской телефонной сети
ВКР: Проектирование аппаратно-программных средств для диагностирования работы абонентской телефонной сети My future profession
My future profession  Условия реализации компетентностного подхода в образовательном пространстве школы
Условия реализации компетентностного подхода в образовательном пространстве школы Презентация на тему Правила безопасного поведения детей на железнодорожном транспорте
Презентация на тему Правила безопасного поведения детей на железнодорожном транспорте В семье пополнение: первая помощь при детской ревности
В семье пополнение: первая помощь при детской ревности Литературная викторина
Литературная викторина Писатели и поэты РоссииКраткая биография
Писатели и поэты РоссииКраткая биография Урок по физике: обобщение по теме «Электричество»
Урок по физике: обобщение по теме «Электричество» Зоя Анатольевна Космодемьянская
Зоя Анатольевна Космодемьянская Организация соревнований
Организация соревнований Птицы лесов, садов и парков
Птицы лесов, садов и парков Какова внешнеполитическая деятельность Наполеона Бонапарта?
Какова внешнеполитическая деятельность Наполеона Бонапарта?