Задание №15 (отрезки)

Функция для отрицания
В Питоне есть встроенное отрицание not, но с ним надо быть аккуратнее, т.к. при его использовании может нарушиться порядок выполнения операций.
Чтобы избежать ошибок, можно написать собственную функцию для отрицания:
def NOT(x):
return not x
Эта функция позволит избежать проблемы с нарушенным порядком выполнения операций.

Логические операции в Питоне
Для отрицания ¬ будем использовать собственную функцию NOT с предыдущего слайда.
Конъюнкция ∧ заменяется на and
Дизъюнкция ∨ в Питоне заменяется на or
Эквиваленция ≡ в Питоне пишется как ==
Не равно ≠ в Питоне обозначается как !=
Импликацию → можно реализовать через сравнение: <=

Задача 1

На числовой прямой даны два отрезка: P = [8, 50] и Q = [27, 76].
Отрезок A таков, что формула
¬ (x ∈ A) → ¬ (¬ (x ∈ P)→ (x ∈ Q))
тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Какова наибольшая возможная длина отрезка A?
Алгоритм решения.
Избавиться в формуле от импликации, инверсии и знаков принадлежности (∈).
Изобразить отрезки на числовой оси.
Построить таблицу истинности для каждого отрезка на прямой.
Решение.
Задача 1

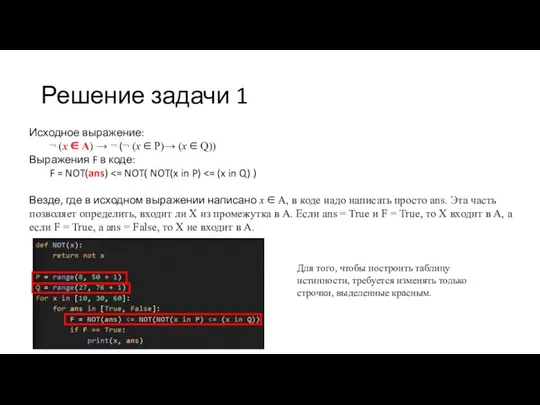
Точки (8, 27, 50 и 76) разбивают числовую прямую на несколько интервалов, для каждого из которых можно определить значение логического выражения
значения формул на концах отрезков не рассматриваются , так как это не влияет на решение.
Решение задачи 1

По условию выражение должно быть равно 1 при любых значениях X,
отсюда можно найти, каким должно быть значение A для каждого интервала.
Проанализировав таблицу видим, что наибольшая длина отрезка А → 76-8 =68
Ответ: 68
Решение задачи 1

Для того, чтобы решить задание, требуется упростить исходную формулу и построить таблицу истинности для каждого отрезка на прямой. Это можно сделать не только математически, но и с помощью программы на Питоне.
P = [8, 50], Q = [27, 76], F = ¬ (x ∈ A) → ¬ (¬ (x ∈ P)→ (x ∈ Q))
Решение задачи 1
В программе нужно изменять только код, выделенный красным.
На следующем слайде объяснение того, как работает программа.

С помощью следующих двух строчек кода:
P = range(8, 50 + 1)
Q = range(27, 76 + 1)
генерируются отрезки [8; 50] и [27, 76]. +1 нужен потому, что range в Питоне работает немного "странно": range(A, B) возвращает все числа в промежуте [A; B-1]. Т.е. число В в список чисел не попадает! Поэтому мы всегда пишем range(A, B+1).
С помощью кода
for x in [10, 30, 60]:
перебираются числа из каждого промежутка, образованного отрезками P и Q:
Числа необязательно должны быть именно такими, например, вместо числа 10 можно было взять 9 или 26, т.е. любое другое число из интервала (8; 27).
10
30
60
Решение задачи 1

Решение задачи 1
Исходное выражение:
¬ (x ∈ A) → ¬ (¬ (x ∈ P)→ (x ∈ Q))
Выражения F в коде:
F = NOT(ans) <= NOT( NOT(x in P) <= (x in Q) )
Везде, где в исходном выражении написано x ∈ A, в коде надо написать просто ans. Эта часть позволяет определить, входит ли Х из промежутка в А. Если ans = True и F = True, то Х входит в А, а если F = True, а ans = False, то Х не входит в А.
Для того, чтобы построить таблицу истинности, требуется изменять только строчки, выделенные красным.

10
+
30
+
60
+
Решение задачи 1
Вывод программы полностью совпадает с таблицей, полученной математически:
Для чисел 10, 30 и 60 выводится только True. Это значит, что нам подходят промежутки [8; 27], [27; 50] и [50; 76].
Поскольку требовалось найти наибольшую возможную длину А, объединяем подходящие промежутки (все промежутки со знаком +) и получаем отрезок [8; 76]. Его длина: 77 - 8 = 68. Это ответ.

Задача 2

На числовой прямой даны два отрезка: Р = [11, 21] и Q = [15, 40].
Укажите наибольшую возможную длину промежутка А, для которого формула
(х ∈ А) → ¬((х ∈ Р) ≡ (х ∈ Q))
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.
Преобразуем выражение.

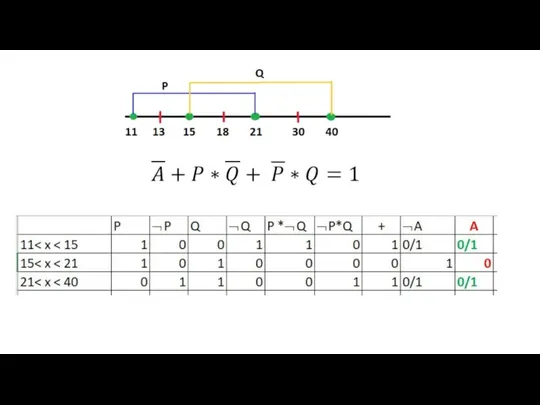
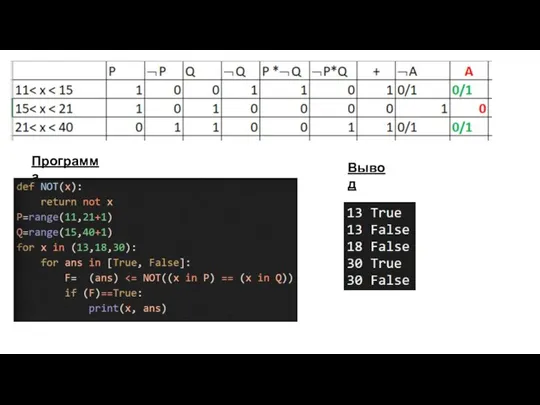
Программа
Вывод

Удовлетворяют два отрезка , на которых А=1.
Это [11,15] и [21,40].
На отрезке [15,21] – А=0!!!
Длины отрезков - 4 и 19
Нужен наибольший- это 19.
Ответ: 19

Про вывод программы

Что означает вывод программы:
если для конкретного числа выводится только True: отрезок с данным числом обязательно должен быть включён в ответ
если для конкретного числа выводится только False: отрезок с данным числом нельзя включать в ответ
если для конкретного числа выводится и True, и False: отрезок с данным числом можно включить в ответ, а можно и не включить, всё зависит от вопроса: если просят наибольшее А, отрезок в ответ попадает, если просят наименьшее А, то отрезок попадёт в ответ только в случае, если вокруг него числа с "True". Пример вывода, когда для наименьшего А отрезок с выводом True/False должен попасть в ответ:
Здесь число 30 (и промежуток, к которому 30 относится) нельзя
выкинуть из ответа, хотя требуется найти наименьшее А. Дело в том, что
числа 20 и 40 обязательно должны попасть в ответ. Т.е. и 20, и 40 должны
принадлежать одному отрезку, тогда число 30 тоже попадёт в этот отрезок.
Про вывод программы

Пример 1. Вывод программы:
10 True
30 True
60 True
Наибольший отрезок: [8; 76]
Наименьший отрезок: [8; 76]
Примеры вывода программы
10
+
30
+
60
+
Пример 2. Вывод программы:
10 True
10 False
30 True
30 False
60 True
Наибольший отрезок: [8; 76]
Наименьший отрезок: [50; 76]
10
+/-
30
+/-
60
+

Пример 3. Вывод программы:
10 True
30 False
60 True
60 False
Наибольший отрезок: [8; 27] (мы не можем добавить в него [50; 76], т.к. тогда придётся включить и [37; 50])
Наименьший отрезок: [8; 27]
Примеры вывода программы
10
+
30
-
60
+/-
Пример 4. Вывод программы:
10 False
30 True
30 False
60 True
Наибольший отрезок: [27; 76]
Наименьший отрезок: [50; 76]
10
-
30
+/-
60
+

Пример 5. Вывод программы:
10 True
30 True
30 False
60 True
Наибольший отрезок: [8; 76]
Наименьший отрезок: [8; 76] (кусок [27; 50] нельзя выкинуть, потому что отрезки слева и справа должны обязательно попасть в ответ).
Примеры вывода программы
10
+
30
+/-
60
+
Пример 6. Вывод программы:
10 True
10 False
30 False
60 True
60 False
Наибольший отрезок: [50; 76] (у него длина больше, чем у отрезка [8; 27])
Наименьший отрезок: можно ни один отрезок не включать в ответ
10
+/-
30
-
60
+/-

Задача 3

Задача 3
На числовой прямой даны два отрезка: P = [3; 15] и Q = [14;25]. Укажите наибольшую возможную длину такого отрезка A, что формула
тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

Отметим границы отрезков на прямой:
Видно, что отрезок посередине выродился в две точки, т.е. внутри отрезка нет точки, которую можно для проверки. В таком случае можно взять обе точки, 14 и 15:
10
20
14, 15
Решение задачи 3

Вывод программы:
Наибольшая возможная длина А в данном случае будет равна 25 – 3 = 22. Это ответ.
Если бы спрашивали наименьшую возможную длину, надо было бы взять отрезок [14; 15], т.к. только для него выводится True (для остальных отрезков – True/False). В таком случае ответ был бы 15 – 14 = 1.
Решение задачи 3
10
+/-
20
+/-
14, 15
+ +

Самостоятельно

Самостоятельно
1
2

Самостоятельно
3
4

Самостоятельно
5
6

Самостоятельно
7
8