Содержание
- 2. Boolean functions
- 3. Boolean functions
- 4. Boolean functions
- 5. Boolean functions
- 6. Boolean functions
- 7. Boolean functions
- 8. Boolean functions
- 9. Boolean functions
- 10. Boolean expressions and Boolean functions
- 11. Boolean expressions and Boolean functions
- 12. Boolean expressions and Boolean functions
- 13. Boolean expressions and Boolean functionsии
- 14. Boolean expressions and Boolean functions
- 15. Boolean expressions and Boolean functions
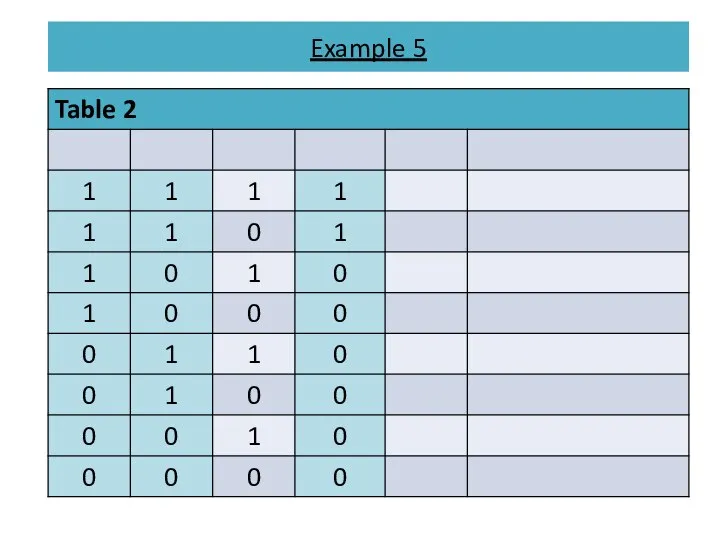
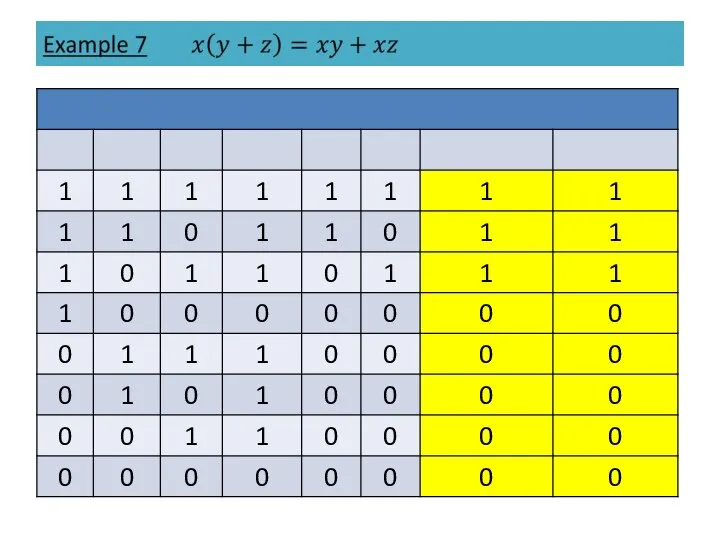
- 16. Example 5
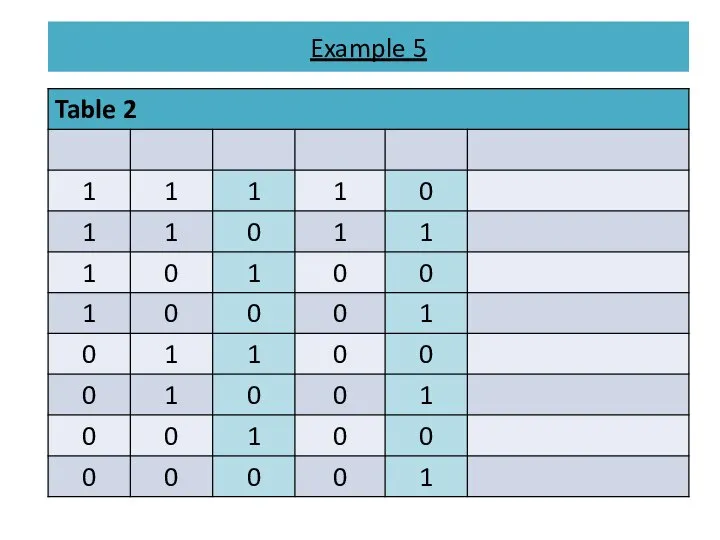
- 17. Example 5
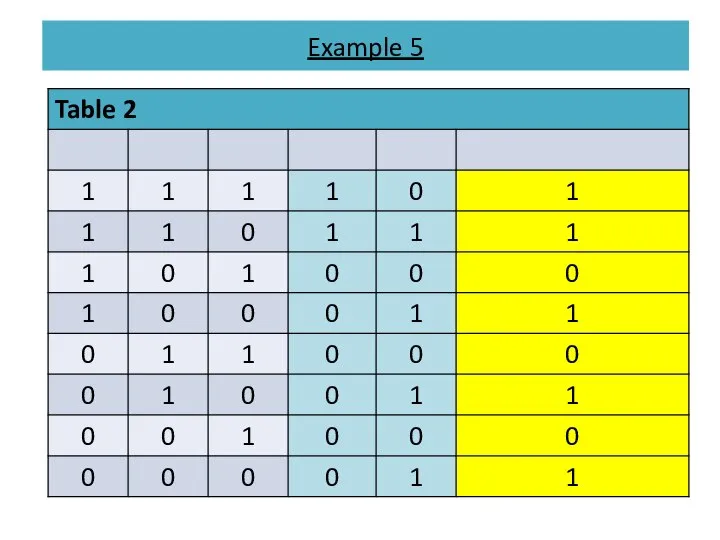
- 18. Example 5
- 19. Boolean expressions and Boolean functions
- 20. Boolean expressions and Boolean functions
- 21. Boolean expressions and Boolean functions
- 22. Boolean expressions and Boolean functions
- 23. Boolean expressions and Boolean functions
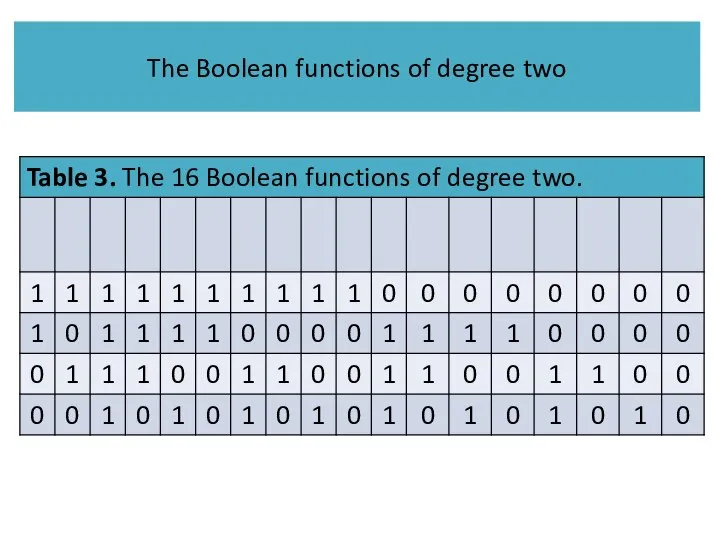
- 24. The Boolean functions of degree two
- 25. Boolean expressions and Boolean functions
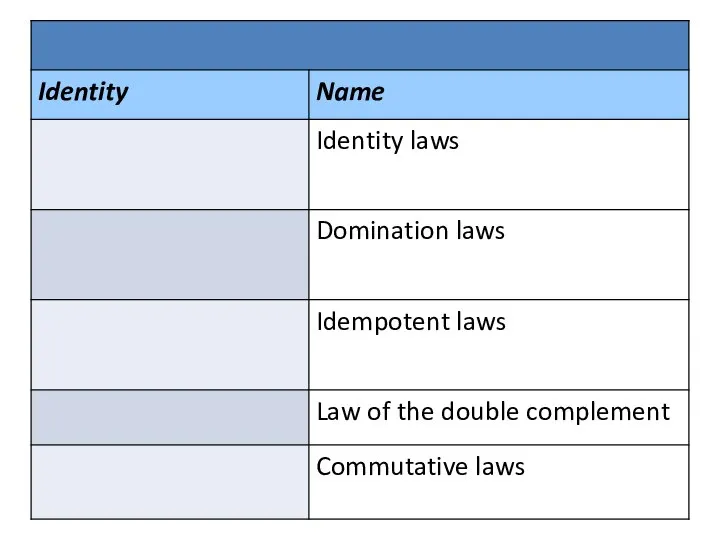
- 26. Identities of Boolean algebra
- 27. Identities of Boolean algebra
- 31. Identities of Boolean algebra Compare these Boolean identities with the logical equivalences and the set identities!
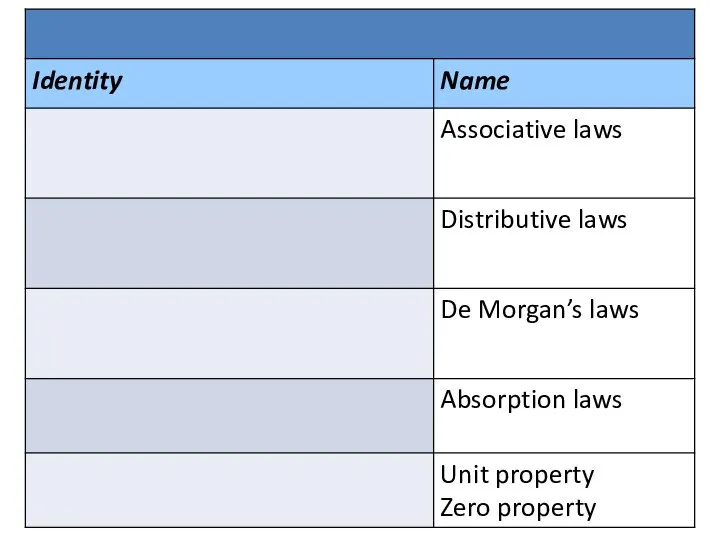
- 32. Identities of Boolean algebra
- 33. Identities of Boolean algebra
- 34. Identities of Boolean algebra
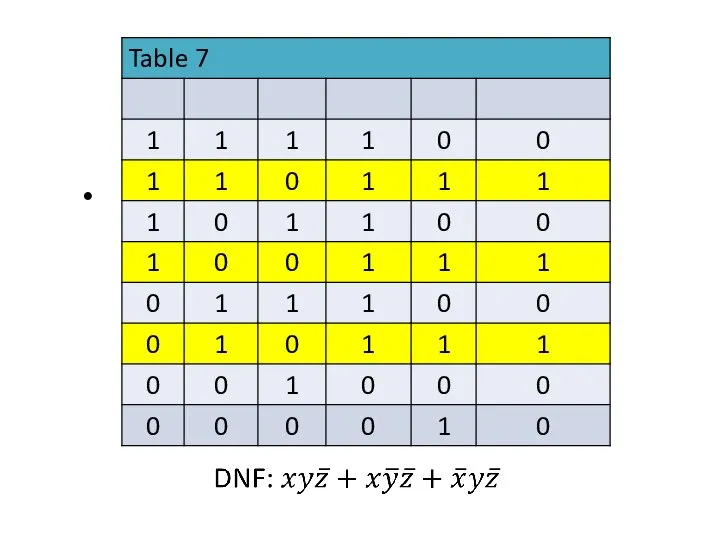
- 35. Disjunctive normal form We now show how any Boolean expression can be expressed in an equivalent
- 36. Disjunctive normal form
- 37. Example of a minterm
- 38. Disjunctive normal form
- 39. A procedure for constructing a Boolean expression representing a function with given values as DNF By
- 40. A procedure for constructing a Boolean expression representing a function with given values as DNF Consequently,
- 41. Disjunctive normal form
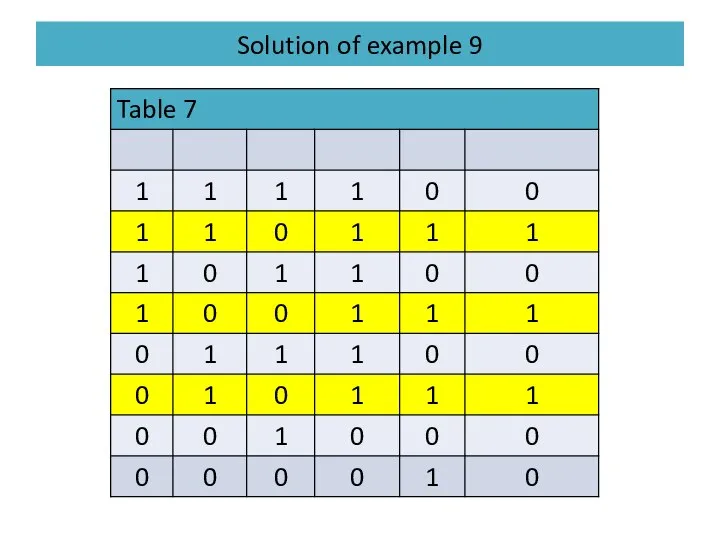
- 42. Solution of example 9
- 44. Conjunctive normal form
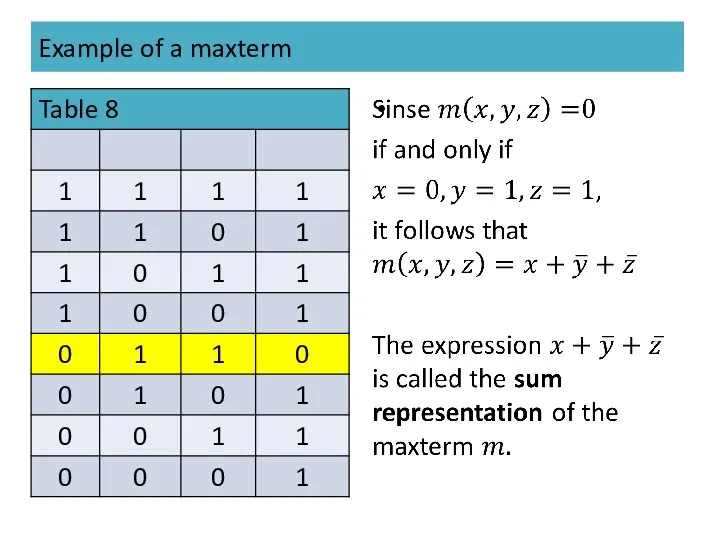
- 45. Example of a maxterm
- 46. Conjunctive normal form
- 47. A procedure for constructing a Boolean expression representing a function with given values as CNF By
- 48. A procedure for constructing a Boolean expression representing a function with given values as CNF Consequently,
- 49. Conjunctive normal form
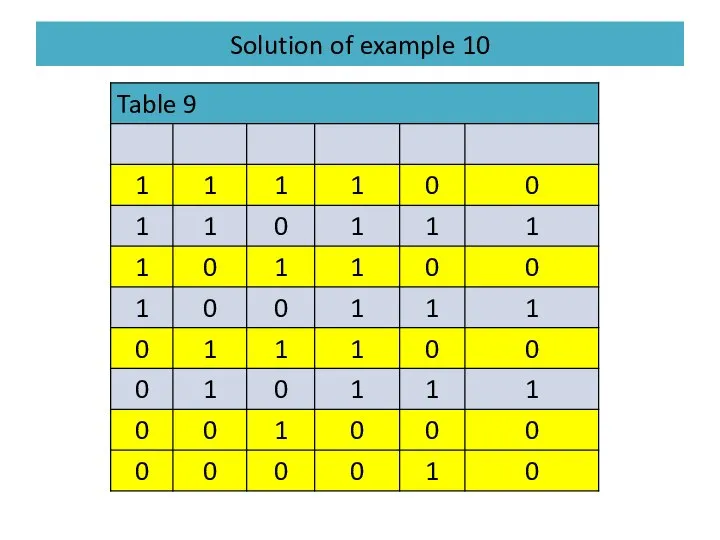
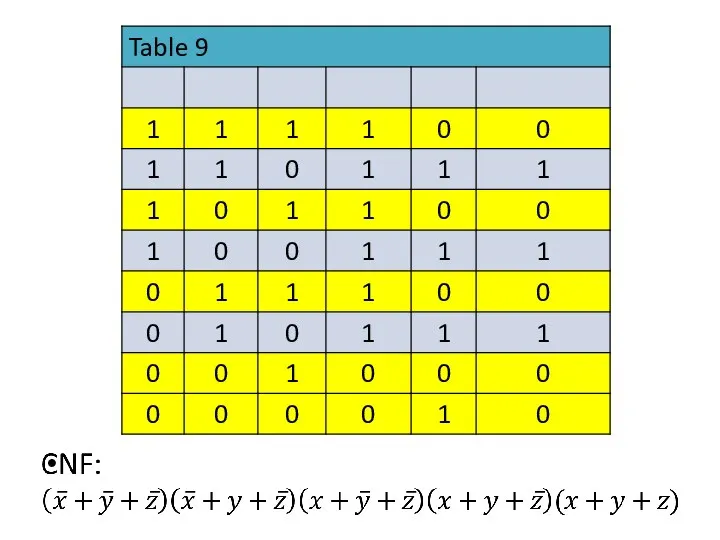
- 50. Solution of example 10
- 52. Functional completeness
- 53. Functional completeness Can we find a smaller set of functionally complete operators? We can do so
- 54. Functional completeness
- 55. Functional completeness
- 56. Functional completeness We have found sets containing two operators that are functionally complete. Can we find
- 57. Functional completeness
- 58. Functional completeness
- 59. Functional completeness
- 60. Biography George Boole, the son of a cobbler, was born in Lincoln, England, in November 1815.
- 61. Biography In his preparation for teaching mathematics, Boole – unsatisfied with textbooks of his day –
- 62. Biography In 1848 Boole published The Mathematical Analysis of Logic, the first of his contributions to
- 64. Скачать презентацию

















































 Songdo International Business District = Odessa
Songdo International Business District = Odessa How Are You Today? 7 лет
How Are You Today? 7 лет Tesco supermarkets
Tesco supermarkets Роберт Бёрнс. Burns Night
Роберт Бёрнс. Burns Night Short u magic circle
Short u magic circle Quiz. Are you good at English? form 4
Quiz. Are you good at English? form 4 Let’s learn the Passive!
Let’s learn the Passive! Повторение 2 класс (1)
Повторение 2 класс (1) The globe or not the globe
The globe or not the globe Halloween: How did we fall in love with pumpkin?
Halloween: How did we fall in love with pumpkin? Указательные местоимения this – these / that - those
Указательные местоимения this – these / that - those Презентация на тему Традиционный рождественский стол
Презентация на тему Традиционный рождественский стол  Past simple questions
Past simple questions Outcomes Upper Intermediate Vocabulary Builder
Outcomes Upper Intermediate Vocabulary Builder Describe the picture
Describe the picture Practical english. Superheroes
Practical english. Superheroes Rhyme
Rhyme Gerund and Infinitive
Gerund and Infinitive Here it is, in front of the beam, between
Here it is, in front of the beam, between Part 4. Questions
Part 4. Questions Fruit travel maze
Fruit travel maze Контроль грамматических навыков по теме Past Simple в 5 классе
Контроль грамматических навыков по теме Past Simple в 5 классе Dress right. Учебник стр. 89 №5
Dress right. Учебник стр. 89 №5 Similes
Similes Числительные
Числительные Get culture !
Get culture ! FOOD. New words
FOOD. New words What is estuary english
What is estuary english