Слайд 3Billboard – Problem
Test all existing subsets
2256 possibilities for the 16x16 board
☹

Слайд 4Billboard – Main Idea
What if we somehow knew the tapped tiles in

the first row?
Слайд 5Billboard – Main Idea
We can try what happens with the row
WOW! It

is easy to find the second one!
Слайд 6Billboard – Main Idea
We can try what happens with the row
WOW! It

is easy to find the second one!
Слайд 7Billboard – Main Idea
Let’s also do it…
The third row becomes evident
… and

so on
Слайд 8Billboard – Solution
Ok, but how to find the first row?
We will try

all possibilities!
Approx. 216 * 162
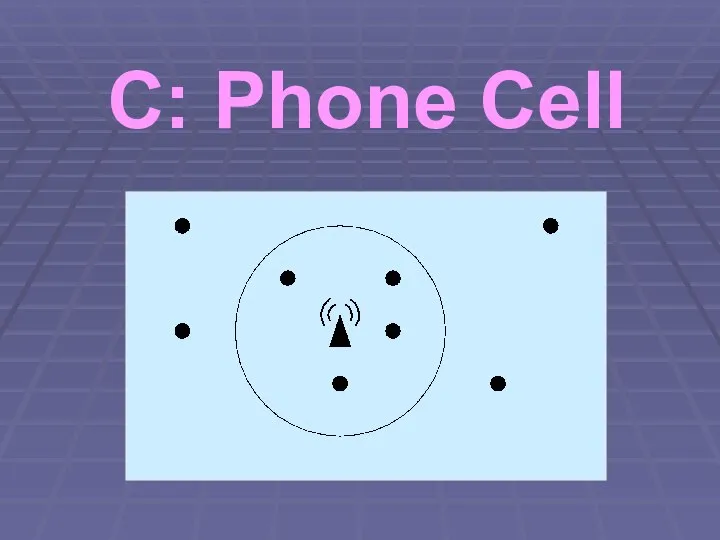
Слайд 10Cell – Problem
Find a circle that covers most points
Center may not be

in an existing point
? Solution will always touch 2 points
Слайд 11Cell – Simple Solution
Take all pairs, find a circle
Then all other points
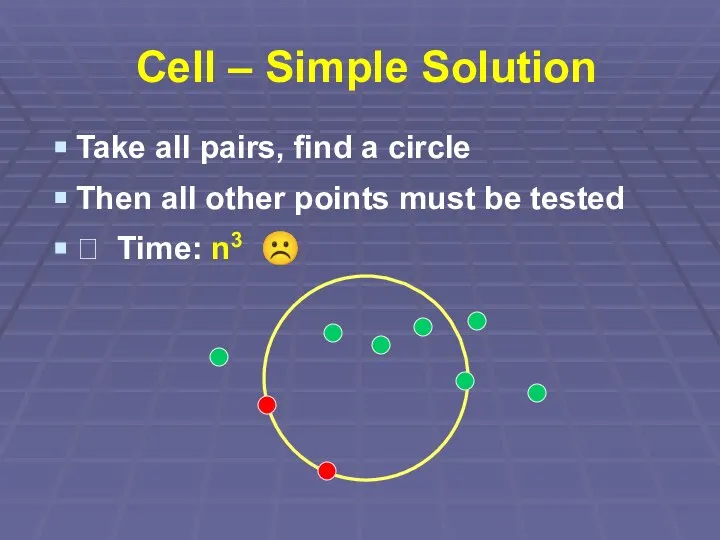
must be tested
? Time: n3 ☹
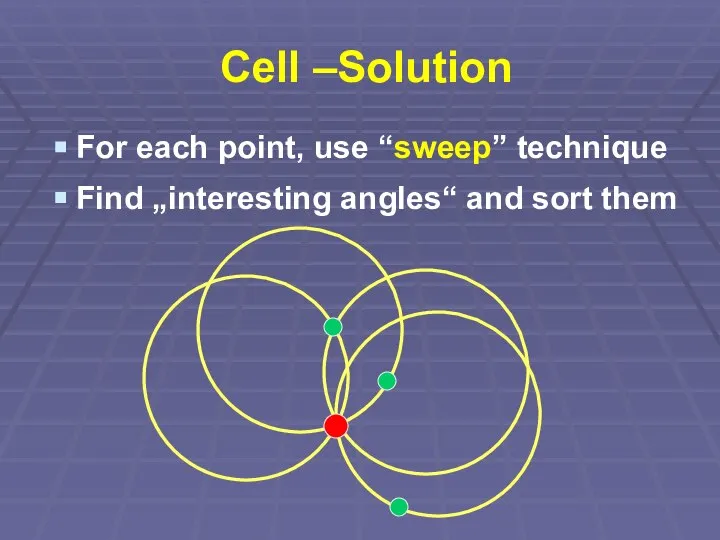
Слайд 12Cell –Solution
For each point, use “sweep” technique
Find „interesting angles“ and sort them
Слайд 13Cell –Solution
One sorting for each point
? Time: n2 . log n
Carefully with

floating point numbers!
Слайд 15Hexagon – Idea
All combinations of 2 green points

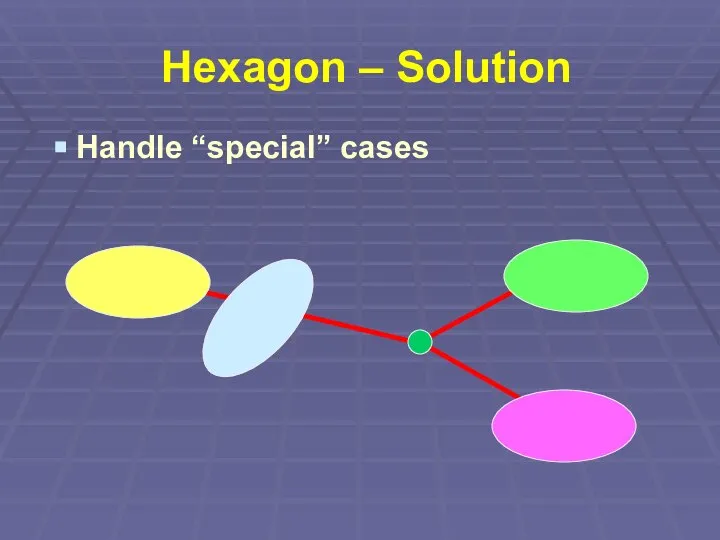
Слайд 16Hexagon – Solution
Handle “special” cases
Слайд 17Hexagon –Solution II
Dynamic Programming
For all area subsets (16), find the best solution

using each parcel
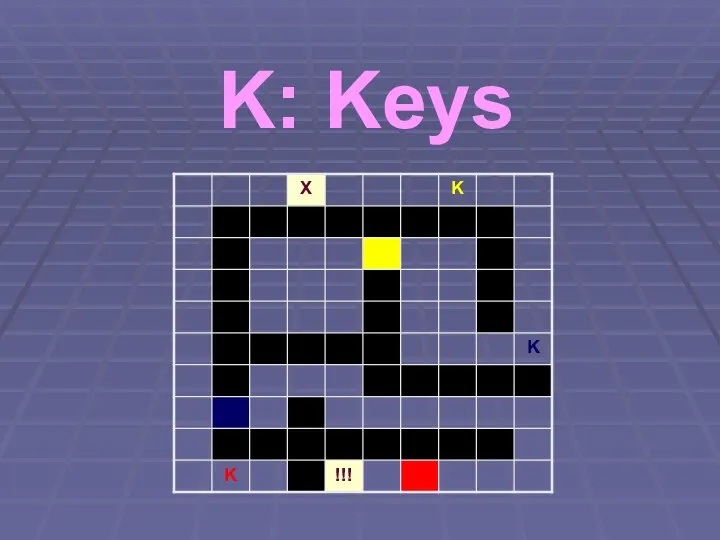
Слайд 19Keys – Idea
Breadth-First search
Combination of position and keys (!)
4 keys => 16

combinations
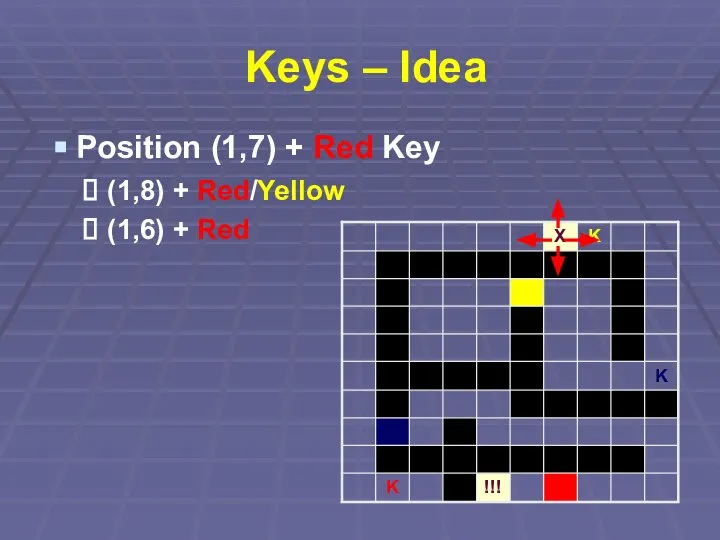
Слайд 20Keys – Idea
Position (1,7) + Red Key
(1,8) + Red/Yellow
(1,6) + Red
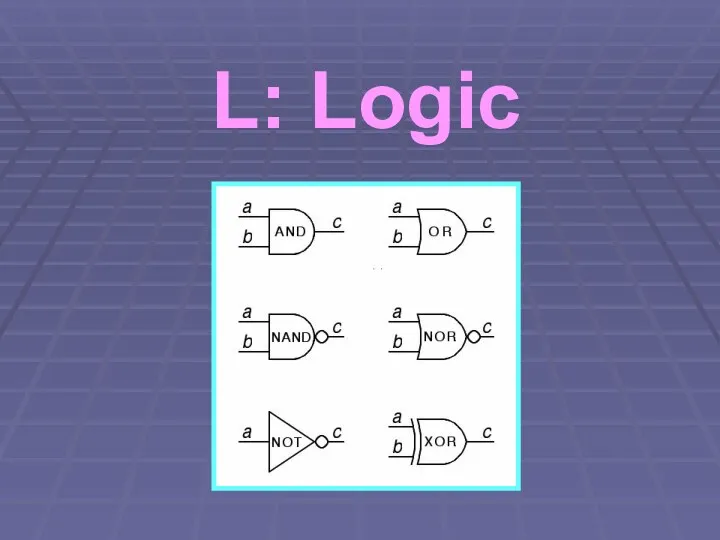
Слайд 22Logic – Problem
Problem? There is no problem
“Only” follow the connections
Compute logical operations

Слайд 23Logic – Potential Pitfalls
Gates with no input
AND ? 1
OR ? 0
XOR ?

0
Слайд 24Logic – Potential Pitfalls
Splitting and joining paths
=> We must remember, what has
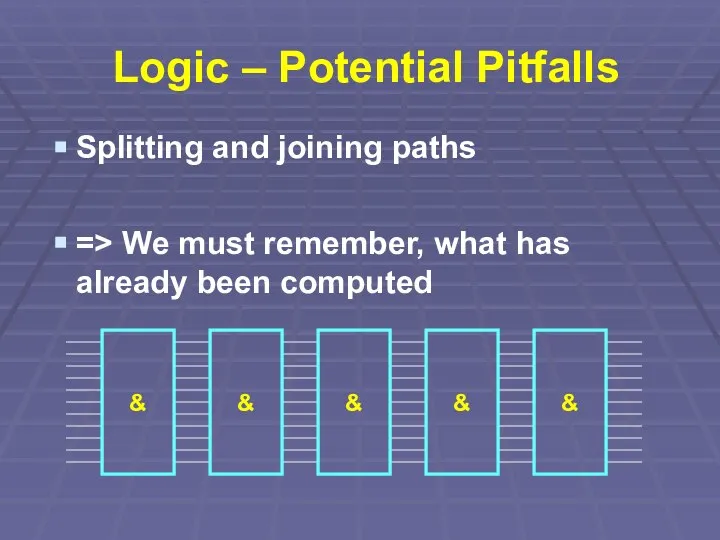
already been computed
&
&
&
&
&
Слайд 25N: Numbers
10101010100101-2 = -10907

Слайд 26Numbers – Solution
TO decimal:
Use the formula in the problem statement
4257-10 = -4000

+ 200 – 50 + 7 = -3843
Слайд 27Numbers – Solution
FROM decimal:
Use remainders (modulo)
Careful with the negative numbers!
4237 mod 10

= 7 -> 423
-423 mod 10 = 7 -> -43
43 mod 10 = 3 -> 4
-4 mod 10 = 6 -> -1
1 mod 10 = 1
-> 16377
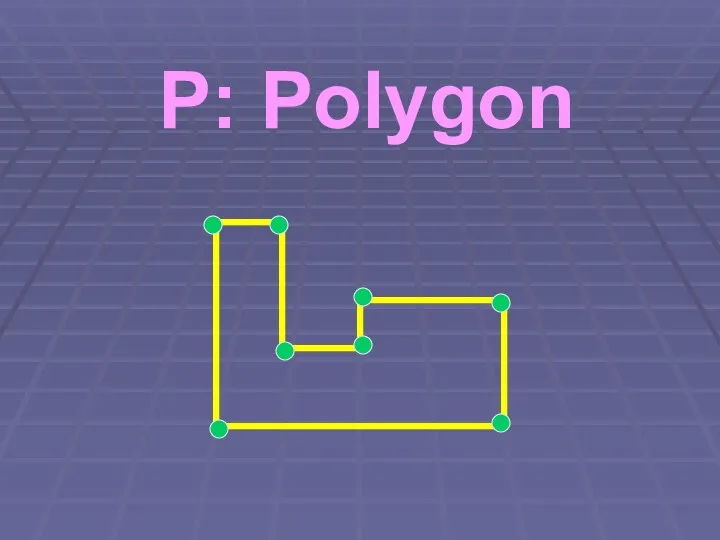
Слайд 29Polygon – Problem
Find the order of polygon vertices

Слайд 30Polygon – Idea
Sort the vertices by their X coordinate
1
3
2
4
5
6
7
8

Слайд 31Polygon – Idea
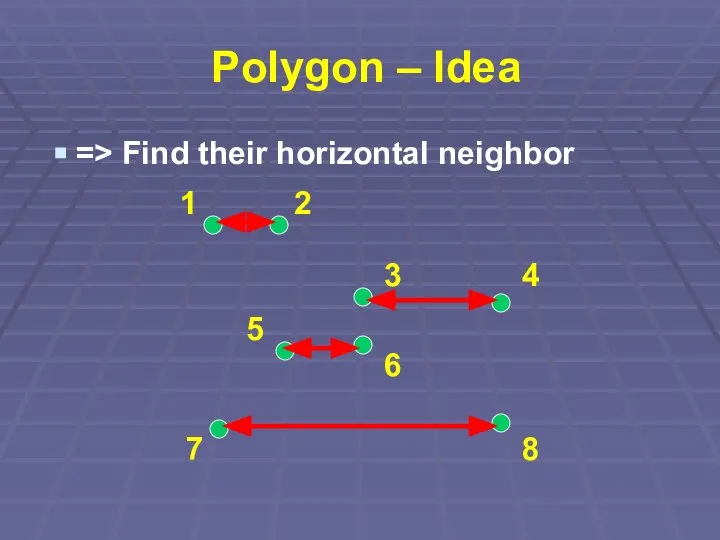
=> Find their horizontal neighbor
1
3
2
4
5
6
7
8
Слайд 32Polygon – Idea
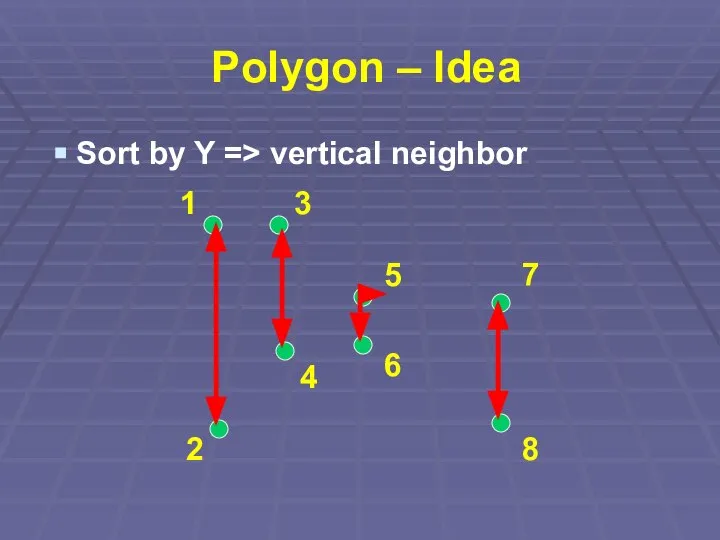
Sort by Y => vertical neighbor
1
5
3
7
4
6
2
8
Слайд 33Polygon – Solution
Now, each vertex knows its neighbors
Start with the first, and

walk around
Слайд 34Polygon – Solution
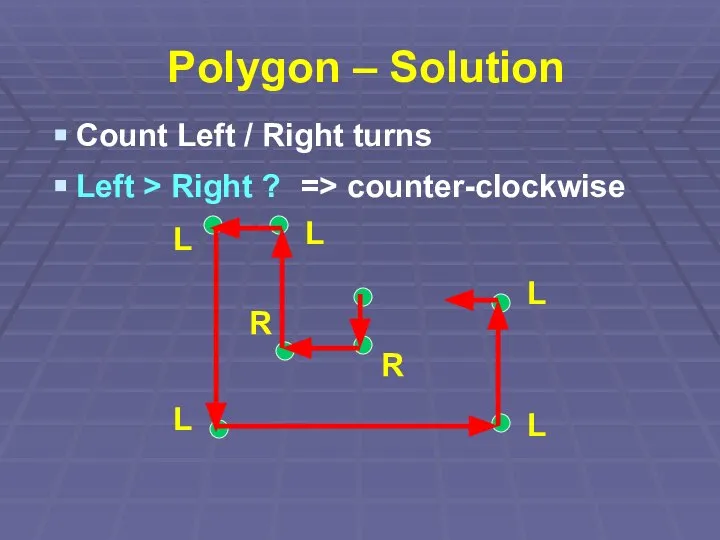
Count Left / Right turns
Left > Right ? => counter-clockwise
R
L
L
L
L
L
R
Слайд 37Sort – Problem
Naive approach – reverse in an array
Little bit better: remember

reversed
Quadratic time ? 100 0002 ☹
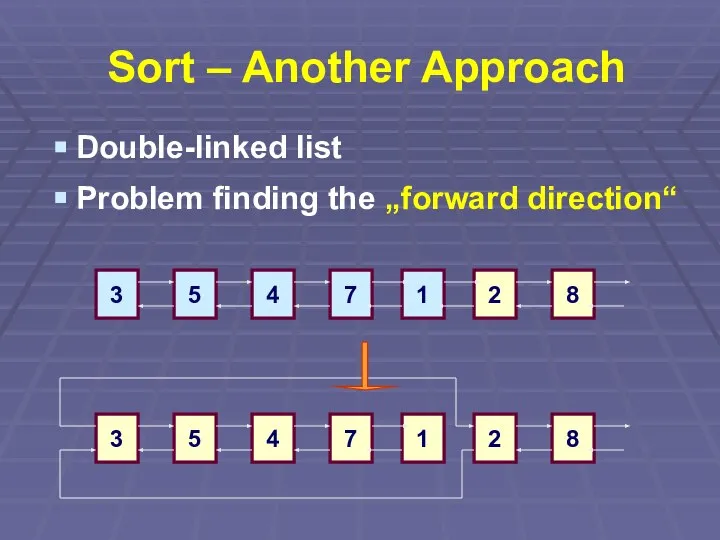
Слайд 38Sort – Another Approach
Double-linked list
Problem finding the „forward direction“
5
4
7
1
2
8
3
5
4
7
1
2
8
3
Слайд 39Sort – Solution
Combined solution: use both
Linked list + array of reversed
The array

time: O(rev_before)
After SQRT(n) steps: reorder
? n.SQRT(n) time
Слайд 40Sort – Solution II
Other possibilities - ???
Heap
Interval Trees
… ?

Слайд 42Water – Problem
Find the Center of Mass
Amount of water with the lowest

center
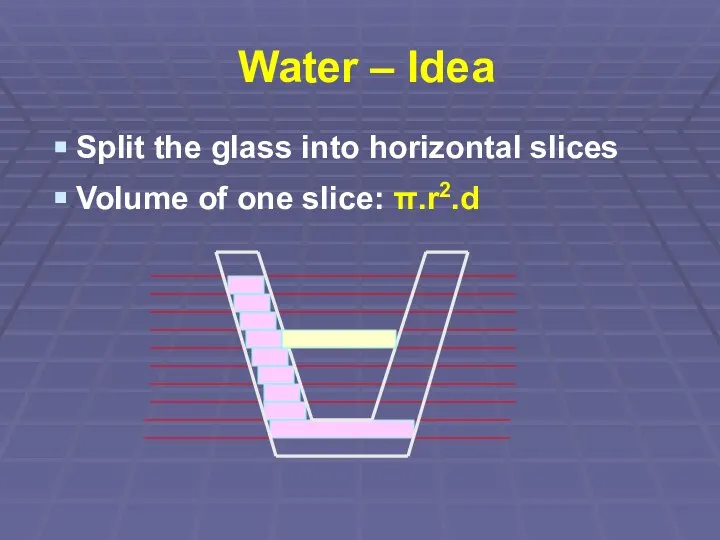
Слайд 43Water – Idea
Split the glass into horizontal slices
Volume of one slice: π.r2.d
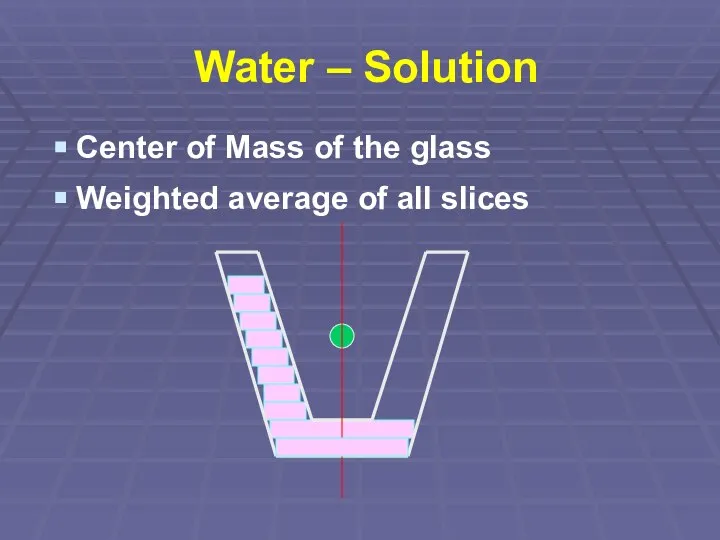
Слайд 44Water – Solution
Center of Mass of the glass
Weighted average of all slices
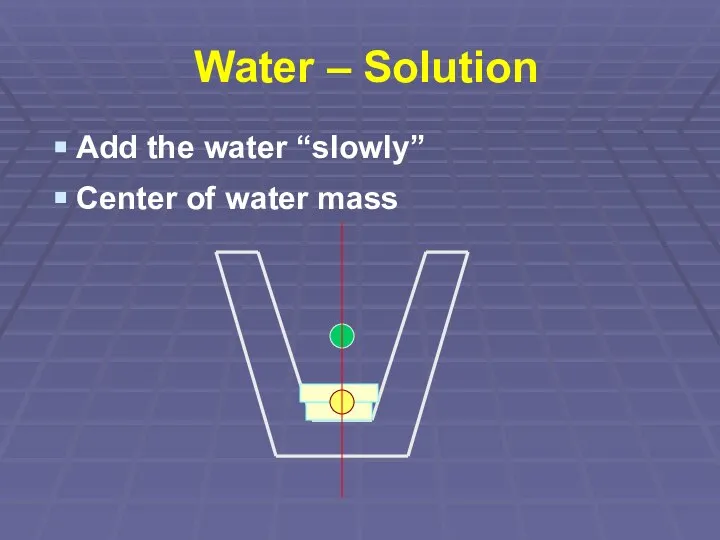
Слайд 45Water – Solution
Add the water “slowly”
Center of water mass
Слайд 46Water – Solution
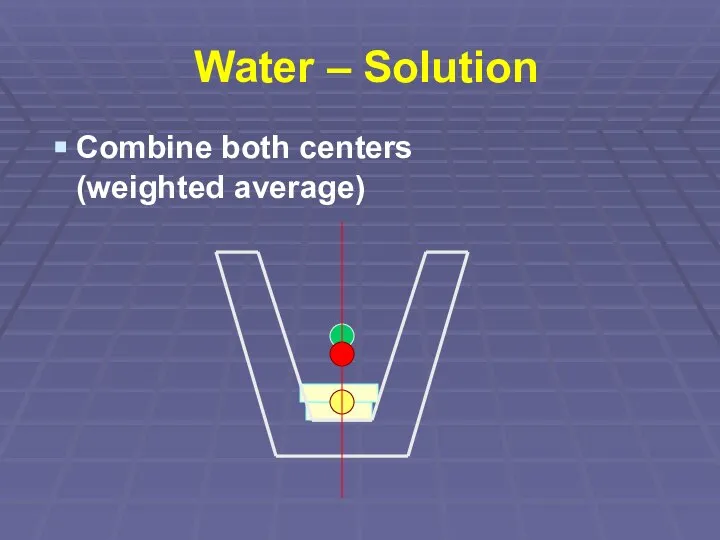
Combine both centers
(weighted average)
Слайд 47Water – Solution
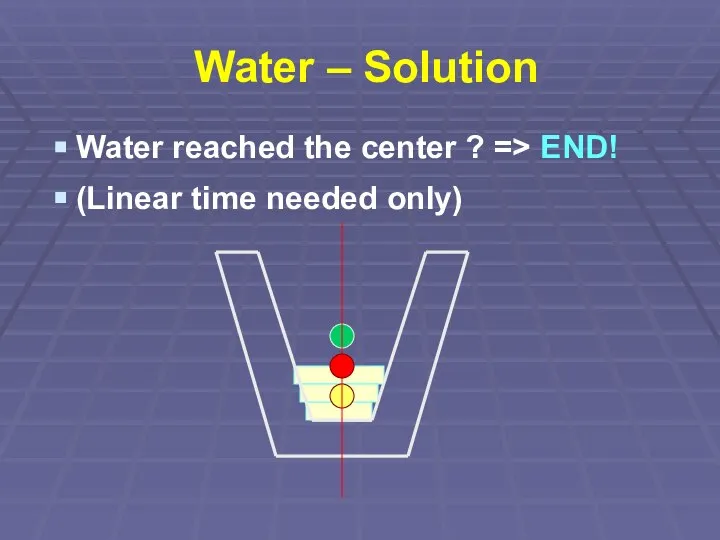
Water reached the center ? => END!
(Linear time needed only)









































 Christmas Crossword
Christmas Crossword Starlight. Module 1,1
Starlight. Module 1,1 What animals is it?
What animals is it? Неправильные глаголы
Неправильные глаголы I have got a …
I have got a … Some Common Errors in English Corrected
Some Common Errors in English Corrected Magic School
Magic School Fair play
Fair play To be names origin
To be names origin Английские идиомы и их русские аналоги
Английские идиомы и их русские аналоги Learning English with animals is fun
Learning English with animals is fun Comparatives and Superlatives
Comparatives and Superlatives Picture stories
Picture stories Do you know this famous address?
Do you know this famous address? Презентация на тему School subjects (3 класс)
Презентация на тему School subjects (3 класс)  Тютчев Фёдор Иванович
Тютчев Фёдор Иванович Фразовый глагол
Фразовый глагол Interactive center of history of the St. Petersburg Metro
Interactive center of history of the St. Petersburg Metro Babbo Natale libro
Babbo Natale libro Steve Jobs
Steve Jobs Ways to express gratitude
Ways to express gratitude Цифровая образовательная платформа Якласс при обучении английскому языку
Цифровая образовательная платформа Якласс при обучении английскому языку Useful words and phrases: • I would like to live
Useful words and phrases: • I would like to live Don’t or Doesn’t. Game
Don’t or Doesn’t. Game A little history
A little history Sustainable products
Sustainable products Lesson 3-4
Lesson 3-4 Презентация на тему NEW YORK CITY
Презентация на тему NEW YORK CITY