Volume

Recall a problem we did way back in Section 5.1…
Estimate the volume of a solid sphere of radius 4.
Each slice can be approximated
by a cylinder:
Radius:
Height:
Volume of each cylinder:
By letting the height of each cylinder approach zero, we could
find the exact volume using a definite integral!!!

Volume as an Integral
Now, we will use similar techniques to calculate volumes of many
different types of solids ? Let’s talk through Figure 7.16 on p.383
The volume of this cylinder is given by
base area x height
And the following sum approximates the volume of the
entire solid:
This is a Riemann sum for A(x) on [a, b]. We get better
approximations as the partitions get smaller ? Their limiting
integral can be defined as the volume of the solid.

Definition: Volume of a Solid
The volume of a solid of known integrable cross section area
A(x) from x = a to x = b is the integral of A from a to b,
How to Find Volume by the Method of Slicing
1. Sketch the solid and a typical cross section.
2. Find a formula for A(x).
3. Find the limits of integration.
4. Integrate A(x) to find the volume.

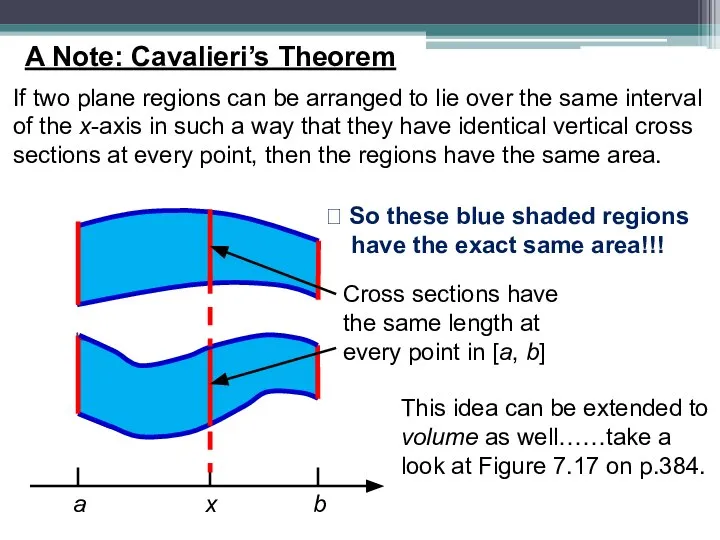
A Note: Cavalieri’s Theorem
If two plane regions can be arranged to lie over the same interval
of the x-axis in such a way that they have identical vertical cross
sections at every point, then the regions have the same area.
a
x
b
Cross sections have
the same length at
every point in [a, b]
? So these blue shaded regions
have the exact same area!!!
This idea can be extended to
volume as well……take a
look at Figure 7.17 on p.384.

Our First Practice Problem
A pyramid 3 m high has congruent triangular sides and a square
base that is 3 m on each side. Each cross section of the pyramid
parallel to the base is a square. Find the volume of the pyramid.
Let’s follow our four-step process:
1. Sketch. Draw the pyramid with its vertex at the origin and its
altitude along the interval . Sketch a typical cross
section at a point x between 0 and 3.
2. Find a formula for A(x). The cross section at x is a square x
meters on a side, so

Our First Practice Problem
A pyramid 3 m high has congruent triangular sides and a square
base that is 3 m on each side. Each cross section of the pyramid
parallel to the base is a square. Find the volume of the pyramid.
Let’s follow our four-step process:
3. Find the limits of integration. The squares go from x = 0
to x = 3.
4. Integrate to find the volume.

Guided Practice
The solid lies between planes perpendicular to the x-axis at x = –1
and x = 1. The cross sections perpendicular to the x-axis are
circular discs whose diameters run from the parabola
to the parabola .
Width of each cross section:
Area of each cross section:
How about a diagram of this solid?

Guided Practice
The solid lies between planes perpendicular to the x-axis at x = –1
and x = 1. The cross sections perpendicular to the x-axis are
circular discs whose diameters run from the parabola
to the parabola .
To find volume, integrate these areas with respect to x:

Guided Practice
The solid lies between planes perpendicular to the x-axis at x = –1
and x = 1. The cross sections perpendicular to the x-axis between
these planes are squares whose diagonals run from the semi-
circle to the semicircle .
How about a diagram of this solid?
Cross section width:
Cross section area:

Guided Practice
The solid lies between planes perpendicular to the x-axis at x = –1
and x = 1. The cross sections perpendicular to the x-axis between
these planes are squares whose diagonals run from the semi-
circle to the semicircle .
Volume:

Guided Practice
The solid lies between planes perpendicular to the x-axis at
and . The cross sections perpendicular to
the x-axis are circular discs with diameters running from the curve
to the curve .
The diagram?
Cross section width:
Cross section area:

Guided Practice
The solid lies between planes perpendicular to the x-axis at
and . The cross sections perpendicular to
the x-axis are circular discs with diameters running from the curve
to the curve .
Volume: