Двойные звезды. Определение масс звезд

Близко расположенные звезды движутся под влиянием сил взаимного гравитационного притяжения.
Две близкие звезды вращаются вокруг общего центра масс.
Иногда две, три и более близких пар звезд образуют кратную систему.

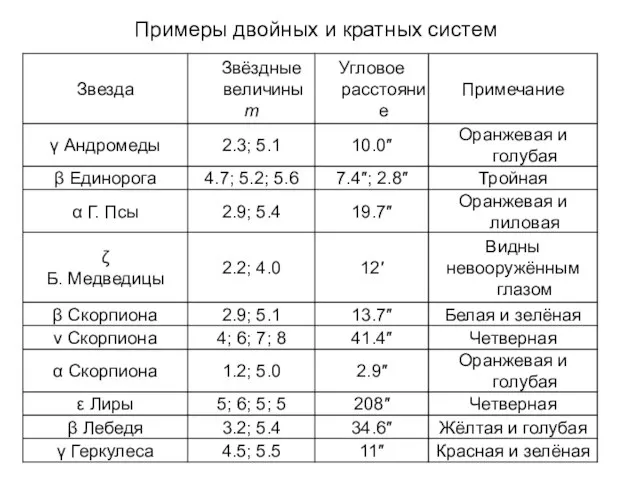
Примеры двойных и кратных систем

Мицар состоит из двух компонент: Мицар A и Мицар B, которые вращаются вокруг общего центра масс с периодом ≈ 2⋅104 лет.
Мицар A состоит из двух звезд, вращающихся с периодом ≈ 20,5 суток !
С древнейших времен известно, что ζ Большой Медведицы (Мицар, 2,17m) имеет образует двойную систему с Алькором (~5m).
Расстояние между звездами ≈17000 а.е., период обращения ≈ 2⋅106 лет.
Мицар и Алькор

Альфа Центавра
Тройная звезда.
Ближайшая звезда к Солнечной системе (4,3 св.года).
Компонента А: желтая звезда, сходная с Солнцем (спектральный класс G2).
Компонента В: оранжевая звезда, L ≈ L☼/3, TE ≈ 4150 K (спектральный класс K5).
Период взаимного обращения компонент А и В ≈ 80 лет.
Третья компонента: Проксима.
Красный карлик, L ≈ 5⋅10−5 L☼
Находится ближе к Солнцу на 2400 а.е., чем компонента А.
Период обращения Проксимы вокруг пары (А + В) – несколько тысяч лет.

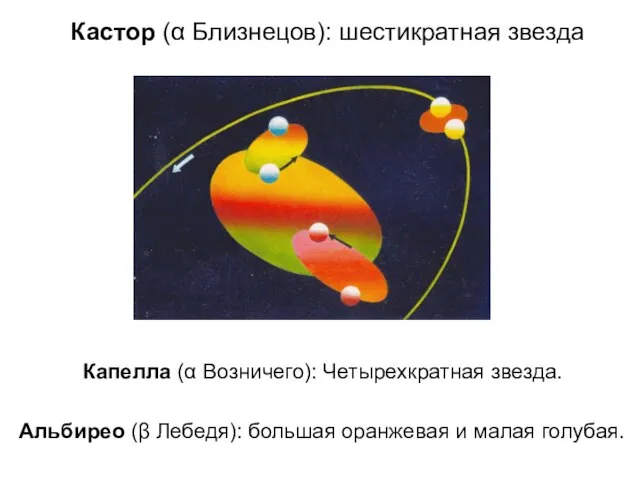
Альбирео (β Лебедя): большая оранжевая и малая голубая.
Капелла (α Возничего): Четырехкратная звезда.
Кастор (α Близнецов): шестикратная звезда

Сириус (α Большого пса)
Компонента А: Белый гигант L ≈ 22 L☼
Компонента В: Белый карлик L ~ 10−3 L☼

Периоды обращения компонентов двойной системы могут быть различными
Обнаружены пары звезд с периодом обращения порядка нескольких часов.
Тесная пара звезд (WZ Стрелы) вращается с периодом ~ 80 мин.

Могут ли компоненты звездной пары вращаться с разными периодами ?
Обязательно ли звездам вращаться в одну и ту же сторону ?
Могут ли компоненты звездной пары вращаться в разных плоскостях ?
Могут ли траектории звезд пересекаться ?
Вопросы:

где G – гравитационная постоянная, r – расстояние от центра масс до эквивалентной материальной точки.
Рассмотрим две звезды с массами m1 и m2, связанные силами взаимного гравитационного притяжения.
Движение двух тел, связанных силами гравитации, характеризуется движением эквивалентной материальной точки с приведенной массой m в центральном поле U.
Динамика системы двух тел

Штриховая линия – траектория эквивалентной материальной точки
Траектории центров звезд пары
подобны эллипсу эквивалентной материальной точки

Штриховая линия – траектория эквивалентной материальной точки
О – центр масс.
Примеры круговых орбит

У более массивной звезды меньший радиус орбиты или меньшая длина большой полуоси.
Начало координат совмещено с центром масс

Массы компонентов двойной звезды могут быть определены:
Для визуально-двойных звезд:
На основании 3-закона Кеплера m1+m2=a3/T2
и соотношения m1r1=m2r2
Для спектрально-двойных:
на основании анализа лучевых скоростей и эффекта Доплера

Более массивная звезда движется медленнее
Дифференцирование по времени соотношения (1) дает уравнение

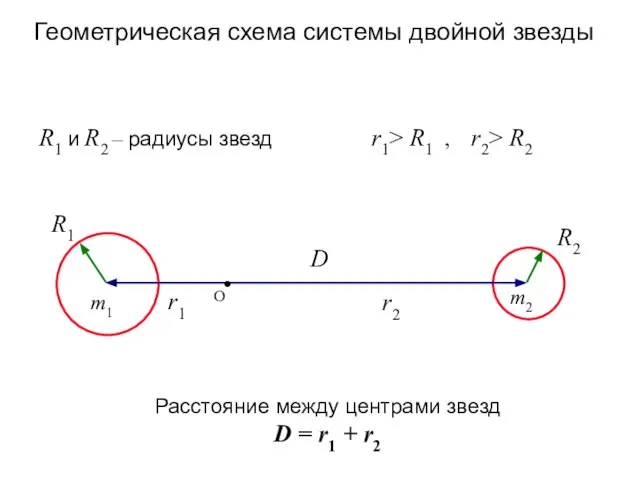
r1> R1 , r2> R2
R1 и R2 – радиусы звезд
Геометрическая схема системы двойной звезды
Расстояние между центрами звезд
D = r1 + r2

Могут ли компоненты звездной пары вращаться с разными периодами ? Нет.
Обязательно ли звездам вращаться в одну и ту же сторону ? Обязательно.
Могут ли компоненты звездной пары вращаться в разных плоскостях ? Нет.
Могут ли траектории звезд пересекаться ? Да. При этом звезды никогда не сталкиваются.
Ответы на вопросы

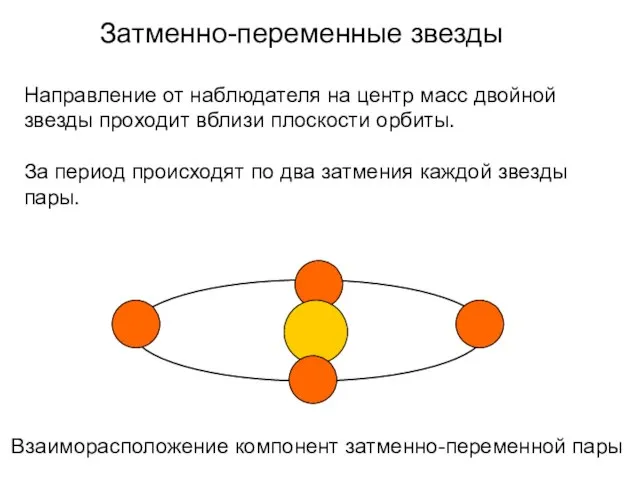
Взаиморасположение компонент затменно-переменной пары
Направление от наблюдателя на центр масс двойной звезды проходит вблизи плоскости орбиты.
За период происходят по два затмения каждой звезды пары.
Затменно-переменные звезды

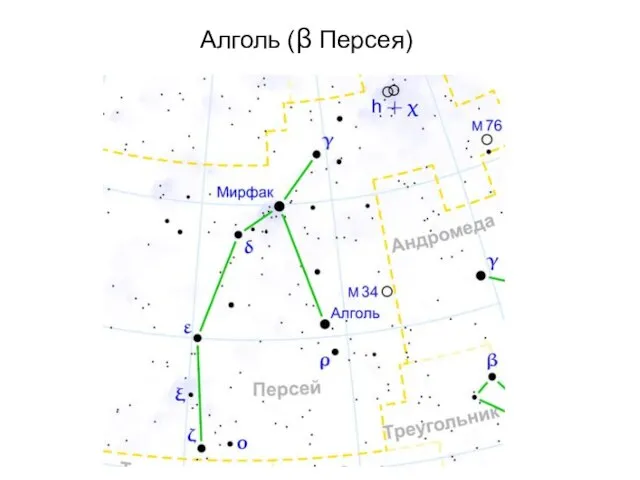
Алголь (β Персея)

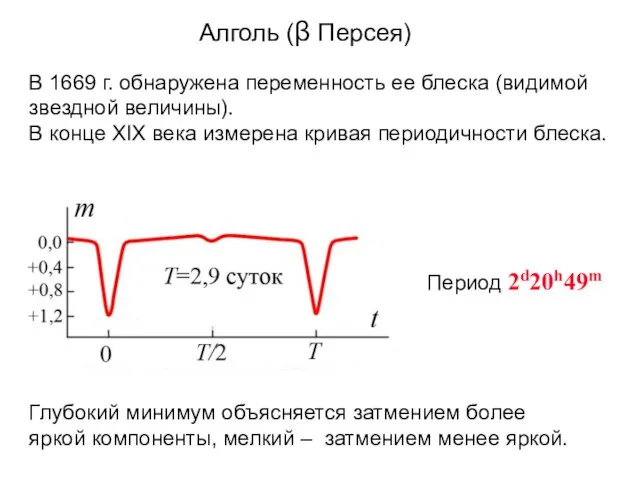
Алголь на арабском языке – Дьявол.
Ещё древние арабы заметили, что с течением времени эта звезда меняет яркость
Созвездие Персея из атласа Гевелия.
Алголь – подмигивающий глаз отрубленной головы горгоны Медузы.

Период 2d20h49m
Глубокий минимум объясняется затмением более яркой компоненты, мелкий – затмением менее яркой.
Алголь (β Персея)
В 1669 г. обнаружена переменность ее блеска (видимой звездной величины).
В конце XIX века измерена кривая периодичности блеска.

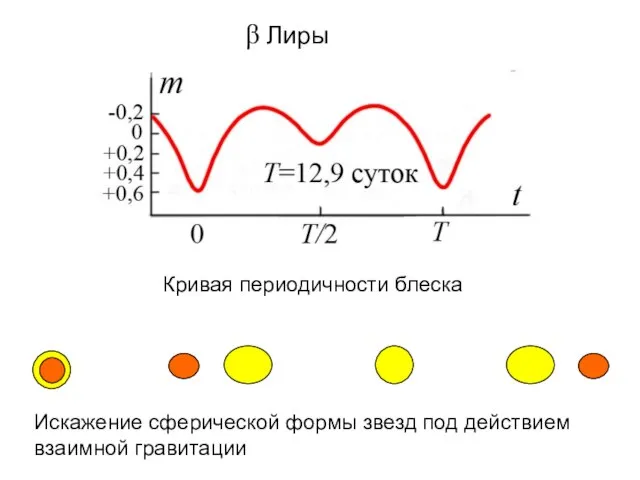
Искажение сферической формы звезд под действием взаимной гравитации
β Лиры
Кривая периодичности блеска

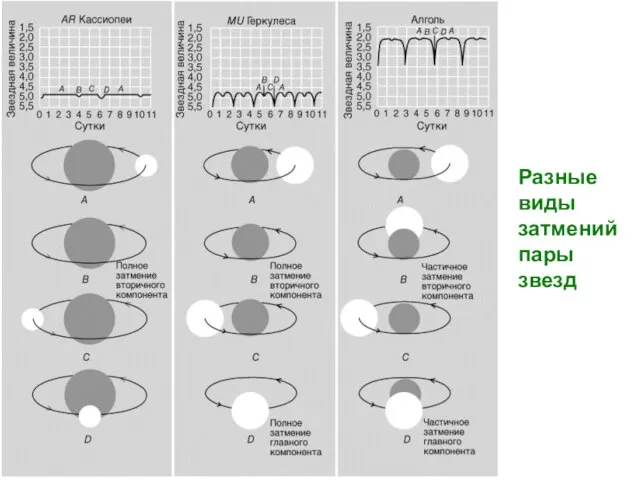
Разные виды затмений пары звезд

Поверхность любой звезды является эквипотенциальной.
Если звезды достаточно удалены друг от друга и угловая скорость обращения вокруг центра масс не очень велика, то форма звезд практически не отличается от сферической.
При нарушении указанных условий форма звезд становится дынеобразной, что и наблюдается.

В начальной стадии обе компоненты двойной звездной системы находятся на главной последовательности. Их радиусы меньше радиусов полостей Роша.
Массообмен между компонентами звездной пары

Более массивная звезда эволюционирует быстрее. После израсходования водорода в центральной части она начинает превращаться в красный гигант.
Вторая, менее массивная звезда остается на главной последовательности, и ее радиус остается неизменным.
Более массивная звезда постепенно разбухает и заполняет свою полость Роша.
Далее начнется перетекание газа и плазмы на соседнюю звезду через внутреннюю точку Лагранжа.
Массообмен между компонентами звездной пары

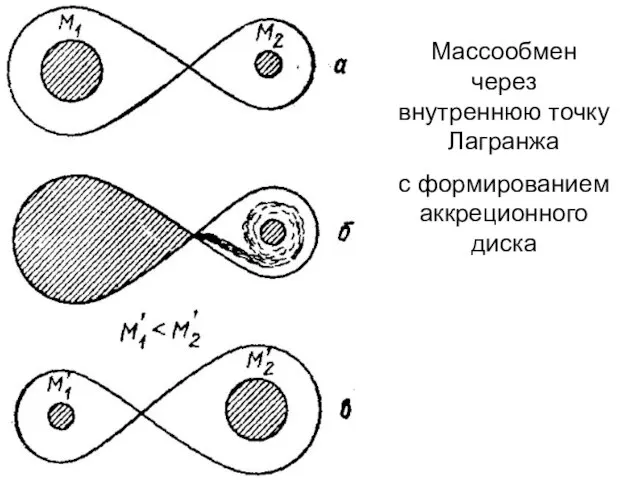
Массообмен
через
внутреннюю точку
Лагранжа
с формированием аккреционного диска

В первом приближении можно считать, что суммарная масса пары звезд остается неизменной.
M1 + M2 = M ≈ const
Размер первой звезды ограничен собственной полостью Роша. Эта звезда не может достичь огромных размеров и останется субгигантом. Светимость этой звезды увеличивается не более, чем на порядок по сравнению с первоначальной.
Обмен массой может происходить до выравнивания масс звезд и даже до обратного соотношения.
Например, если вначале было
M1 = 5 M☼, M2 = M☼ /2 ,
то после массобмена может быть
M2 = 2 M☼

Различные варианты эволюции двойных систем зависят, прежде всего, от масс звезд.
Возможен случай, когда масса второй звезды (на которую перетекает вещество) приобретает массу на порядок больше первой, но при этом еще будет принадлежать главной последовательности.
Пример : Алголь.
Что произойдет дальше с первой звездой ?
Это существенно зависит от её массы.