Популяционная динамика животных и микроорганизмов

Имеется некоторая популяция одного вида (микроорганизмы, зайцы и т.п.), в которой происходят жизненные процессы во всем их многообразии.
Задача. Найти законы изменения численности
популяции во времени.
Основные допущения:
1 . Существуют только процессы размножения и естественной гибели, скорости которых пропорциональны численности особей в данный момент времени.
2. Не учитываем биохимические, физиологические процессы.
3. Нет борьбы между особями за место обитания, за пищу
(бесконечно большое пространство и количество пищи).
4. Рассматриваем только одну популяцию, нет хищников.
Животные: простейшая модель

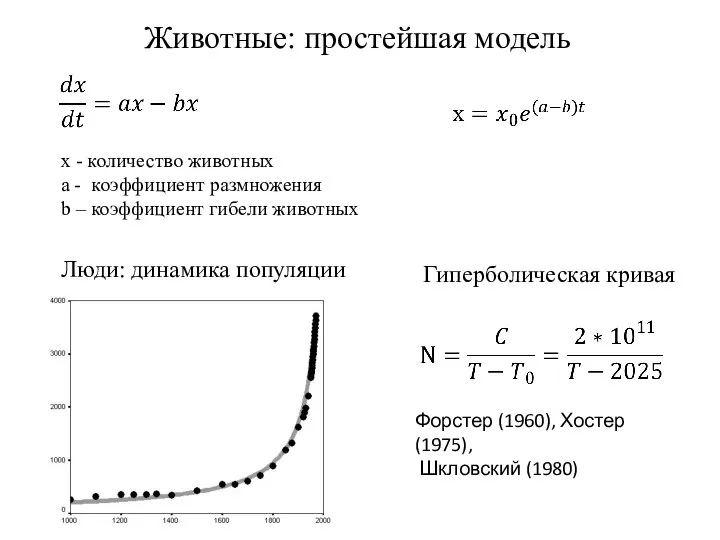
Животные: простейшая модель
x - количество животных
a - коэффициент размножения
b – коэффициент гибели животных

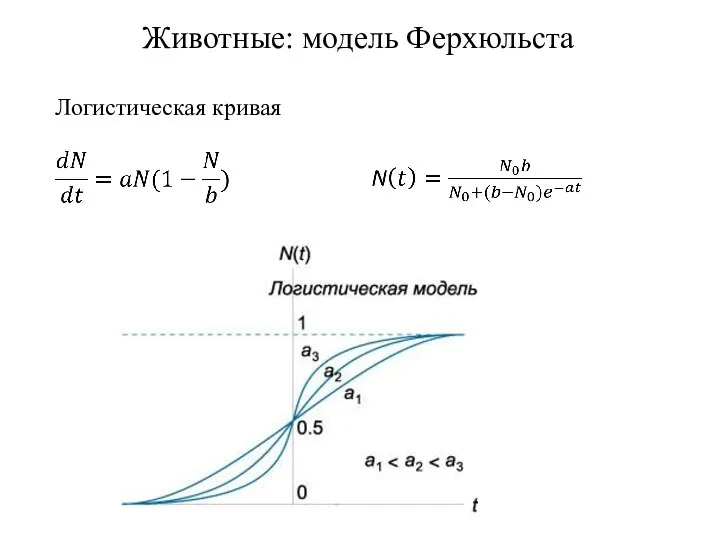
Животные: модель Ферхюльста
Логистическая кривая

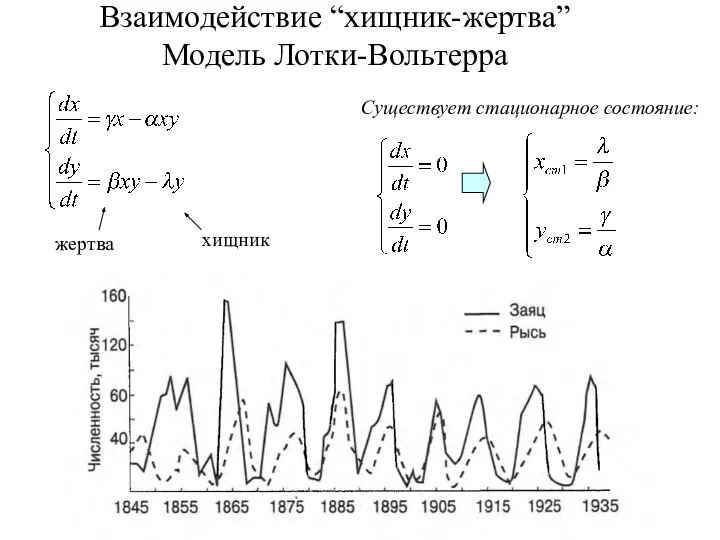
Взаимодействие “хищник-жертва”
Модель Лотки-Вольтерра
жертва
хищник
Существует стационарное состояние:

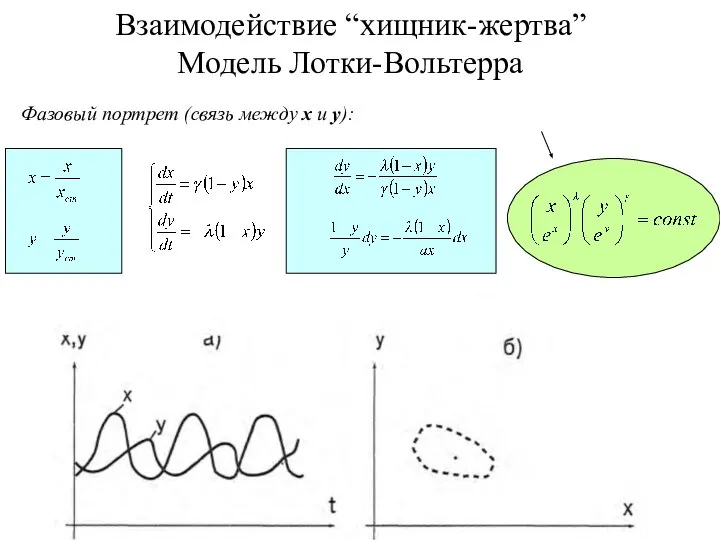
Фазовый портрет (связь между x и y):
Взаимодействие “хищник-жертва”
Модель Лотки-Вольтерра

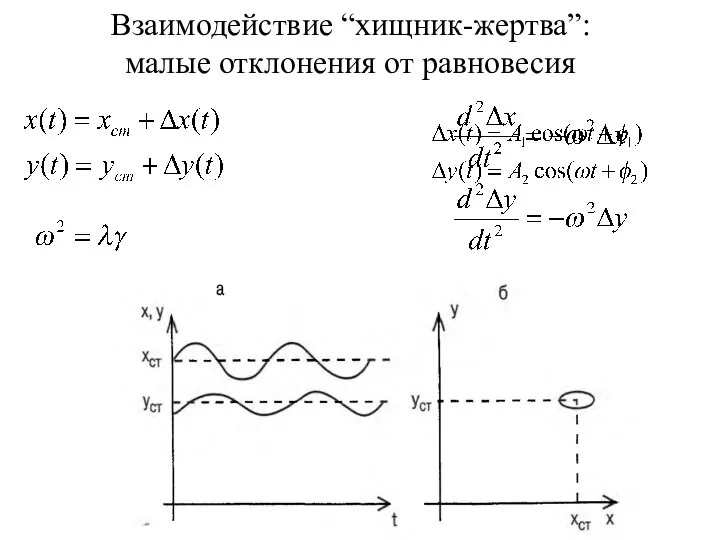
Взаимодействие “хищник-жертва”:
малые отклонения от равновесия

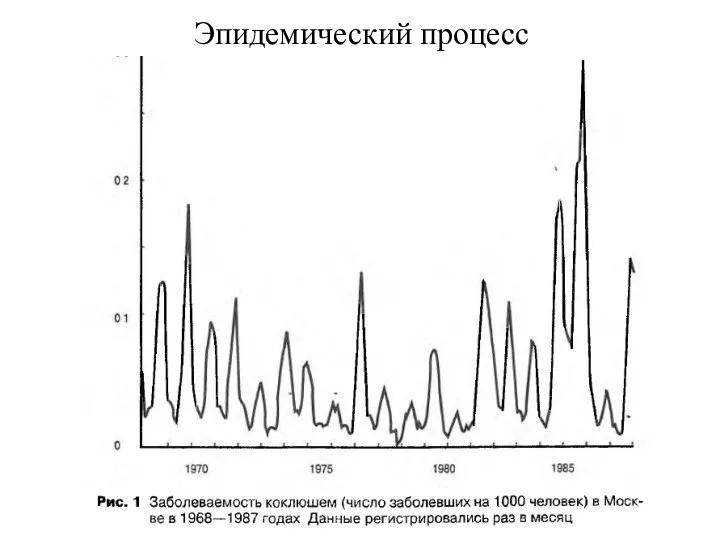
Эпидемический процесс

Моделирование эпидемического процесса
Сделаем ряд упрощений:
1) рассмотрим инфекционные заболевания с пожизненным иммунитетом
2) будем считать, что численность популяции людей не изменяется с течением времени
3) популяция возбудителя однородна
4) популяция людей однородна
5) вероятность смерти человека не зависит от возраста;
6) вероятность выздоровления человека не зависит от времени, прошедшего с момента заражения
7) вероятность передачи инфекции не зависит от времени года

Моделирование эпидемического процесса
Три состояния человека:
1) восприимчивый, т.е. не болеющий и еще не болевший
этим инфекционным заболеванием человек, который впоследствии
может заразиться;
2) инфицированный человек;
3) иммунный, т.е. имеющий иммунитет в результате перенесенного
заболевания человек.

Переход ‘‘восприимчивые” - “инфицированные”
Моделирование эпидемического процесса
Переход “инфицированные” - ”здоровые”
Переход ‘‘восприимчивые” - “умершие”
Переход ‘‘инфицированные” - “умершие”
Рождение ‘‘восприимчивых”

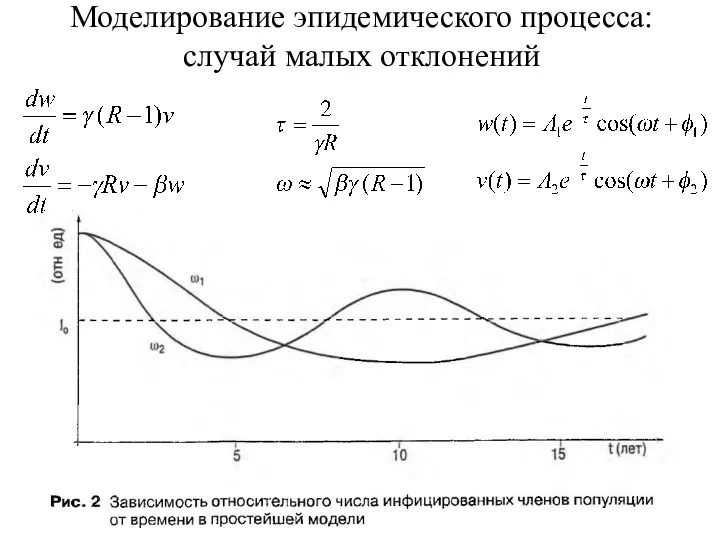
Моделирование эпидемического процесса:
случай малых отклонений

Эпидемический процесс:
усложнение модели
Учет “лаг-фазы” инфекции
Учет заразности инфекции от времени года

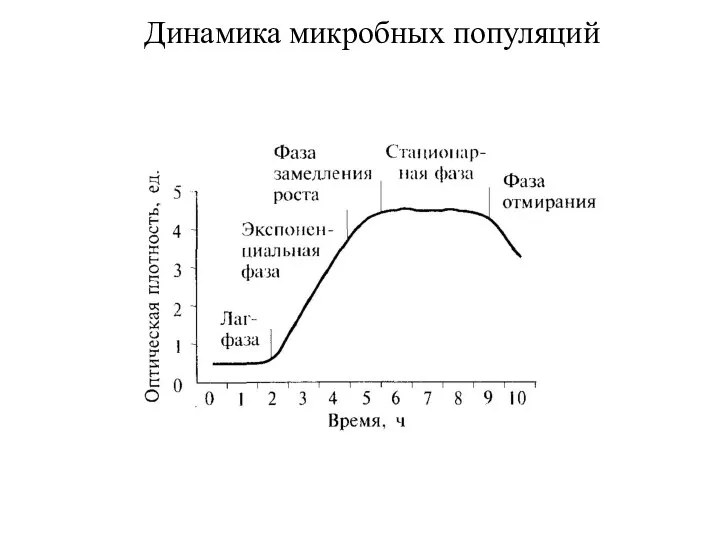
Динамика микробных популяций

Культивирование клеток -> изучение клеточного цикла in vitro
(культуры, линии клеток).
Фазы роста:
1) индукционный (лаг-фаза) – адаптация клеток к среде,
перестройка их метаболизма;
2) экспоненциальный рост (много митозов);
3) линейный рост (мало митозов);
4) замедление роста;
5) стационарная фаза;
6) отмирание культуры.
Причины замедления роста – истощение субстрата,
накопление токсических продуктов и др.
Динамика микробных популяций

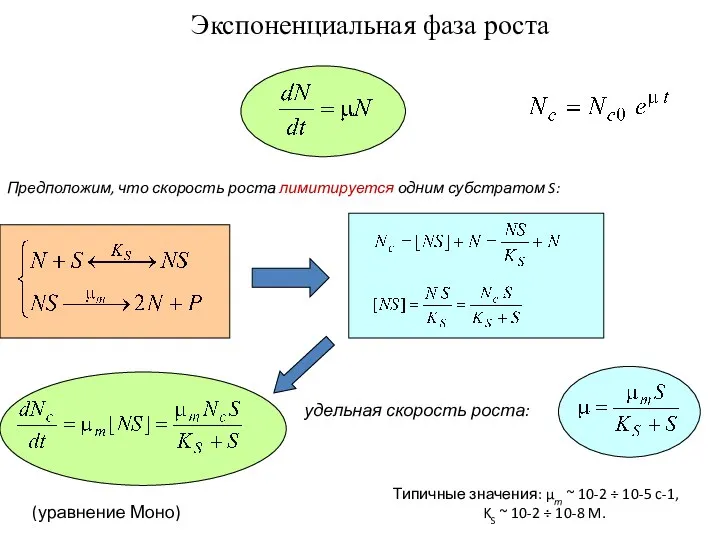
Экспоненциальная фаза роста
Предположим, что скорость роста лимитируется одним субстратом S:
удельная скорость роста:
(уравнение Моно)
Типичные значения: μm ~ 10-2 ÷ 10-5 c-1,
KS ~ 10-2 ÷ 10-8 M.

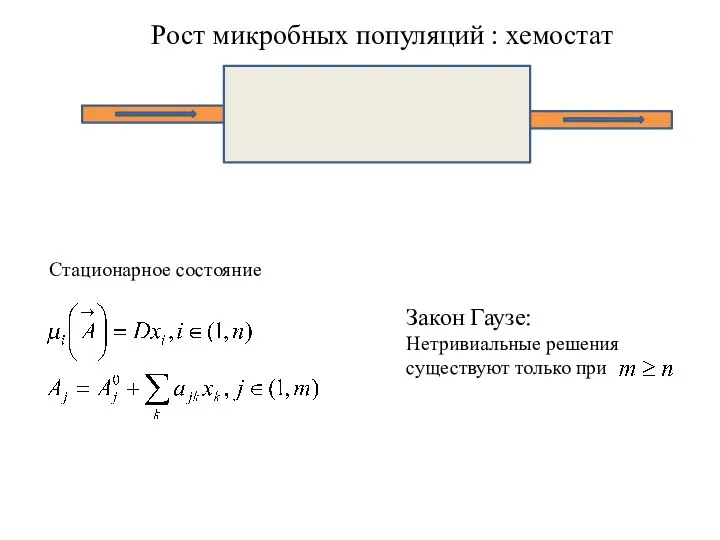
Рост микробных популяций : хемостат
- удельная скорость роста, зависит от концентрации пит. веществ

Рост микробных популяций : хемостат
Стационарное состояние
Закон Гаузе:
Нетривиальные решения существуют только при

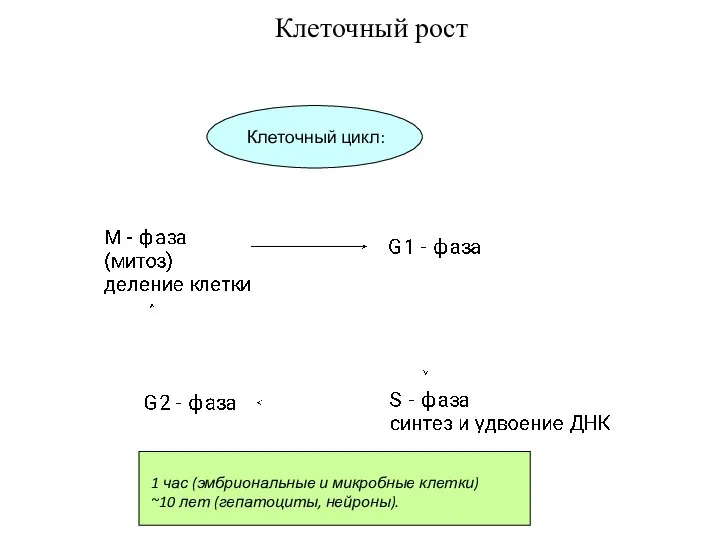
Клеточный рост
Клеточный цикл:
1 час (эмбриональные и микробные клетки)
~10 лет (гепатоциты, нейроны).

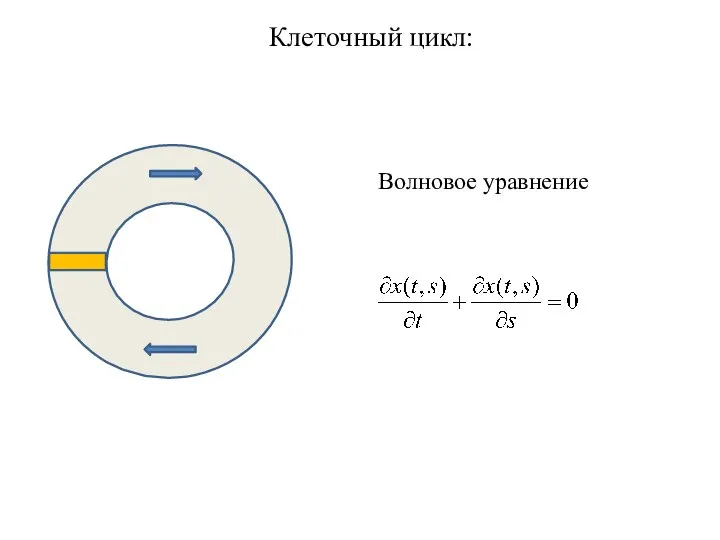
Клеточный цикл:
Волновое уравнение

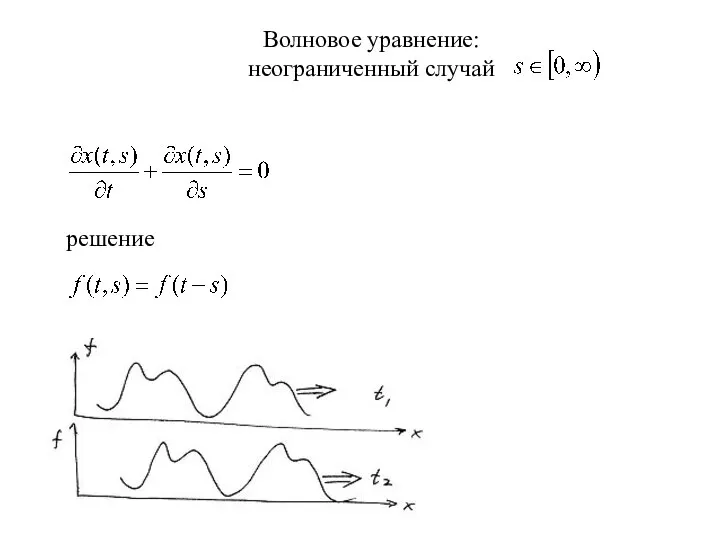
Волновое уравнение: неограниченный случай
решение