Триггеры и колебания в биологии

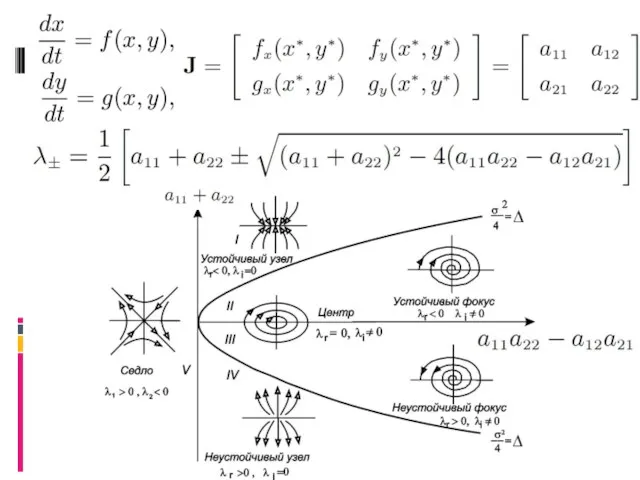
Бифуркационный анализ
Поиск качественных изменений в решении системы дифференциальных уравнений при изменении параметров системы
График зависимости стационарного состояния от бифуркационного параметра называется бифуркационной диаграммой
Бифуркации стационых состояний:
λ (real) <0 -> λr =0 -> λr >0

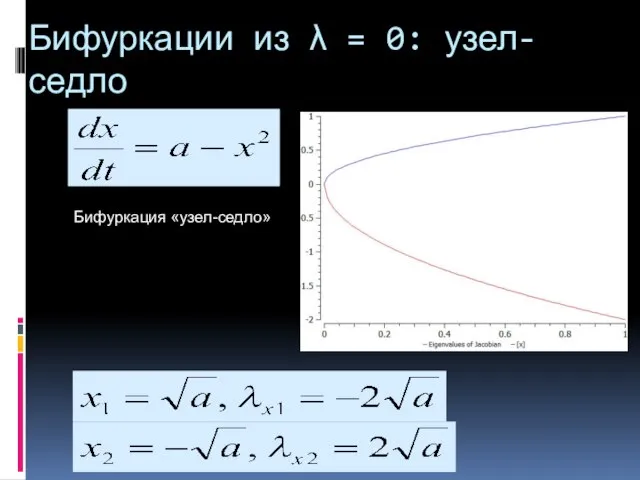
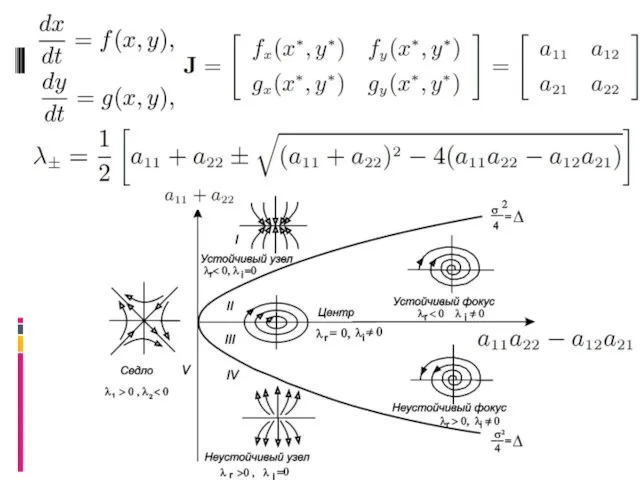
Бифуркация «узел-седло»
Бифуркации из λ = 0: узел-седло

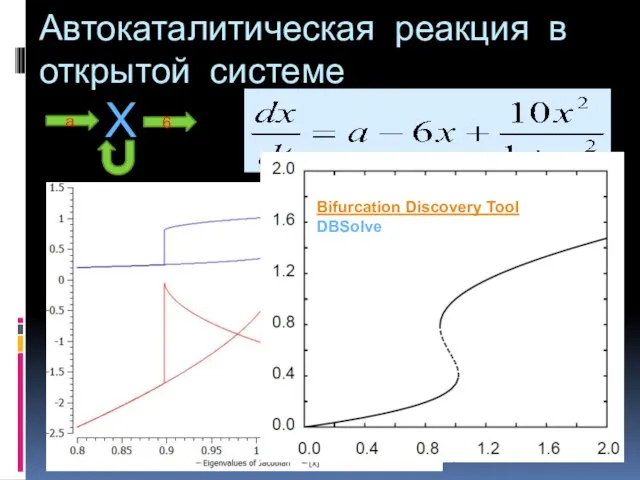
Автокаталитическая реакция в открытой системе
Bifurcation Discovery Tool
DBSolve
X
a
6

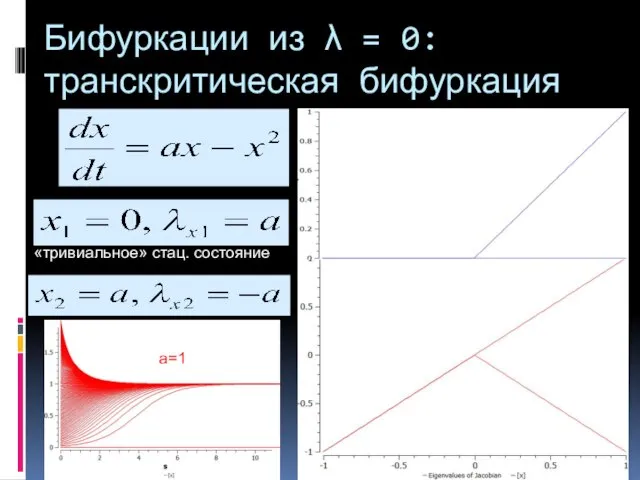
Бифуркации из λ = 0:
транскритическая бифуркация
«тривиальное» стац. состояние
a=1

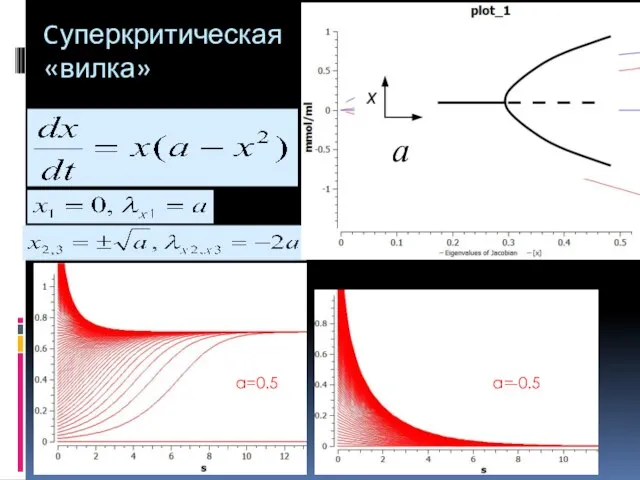
Cуперкритическая «вилка»
a=0.5
a=-0.5

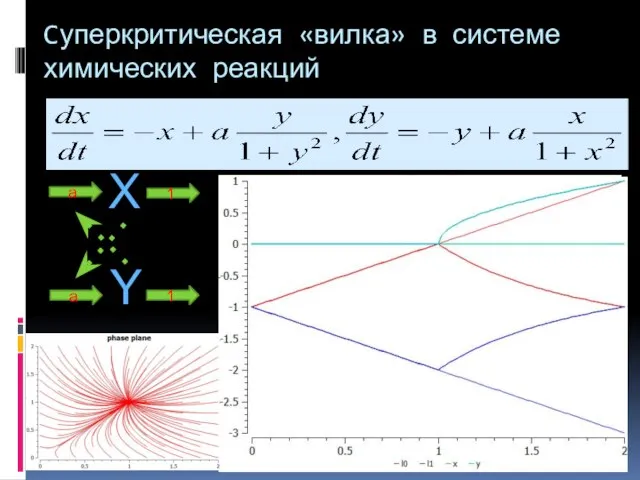
Cуперкритическая «вилка» в системе химических реакций
X
a
1
Y
1
a

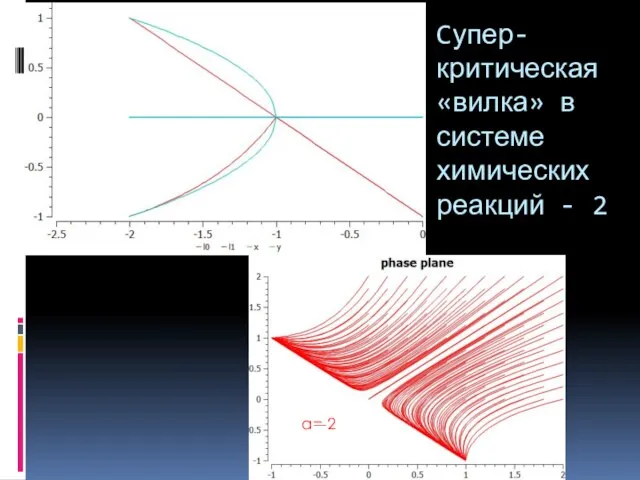
Cупер-критическая «вилка» в системе химических реакций - 2
a=-2

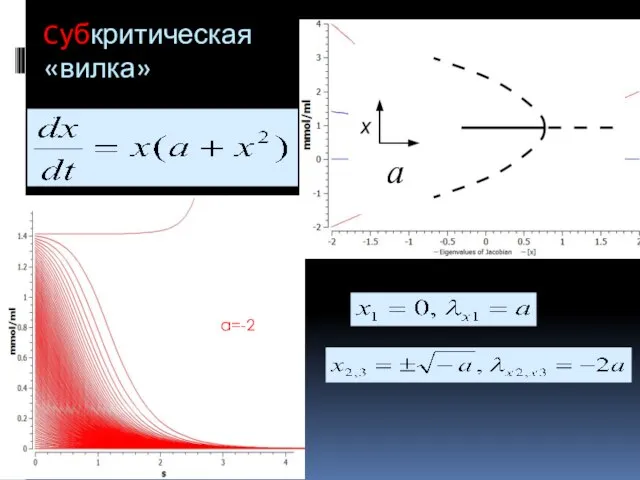
Cубкритическая «вилка»
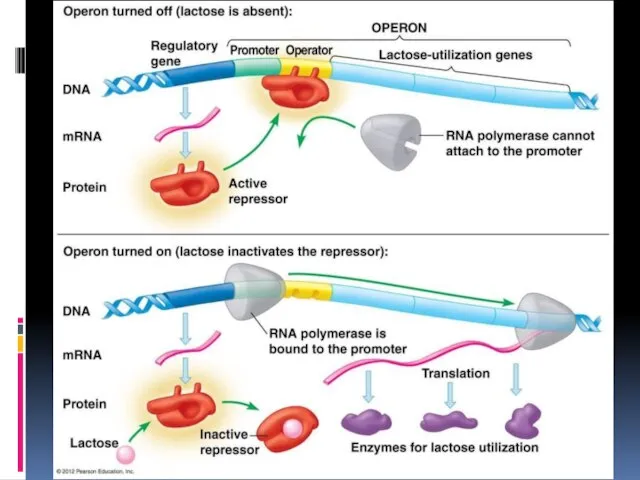
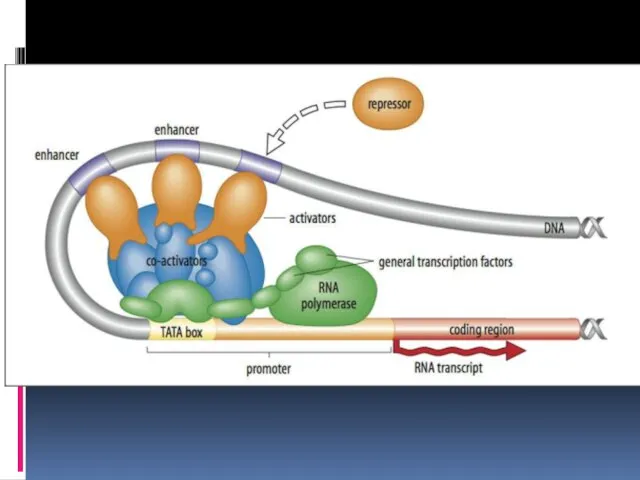
a=-2

Регуляция экспрессии генов
Прокариоты: оперон
Эукариоты: все уровни

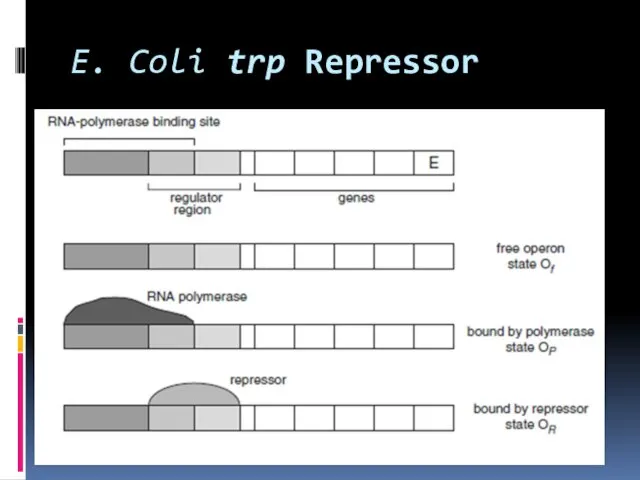
E. Coli trp Repressor

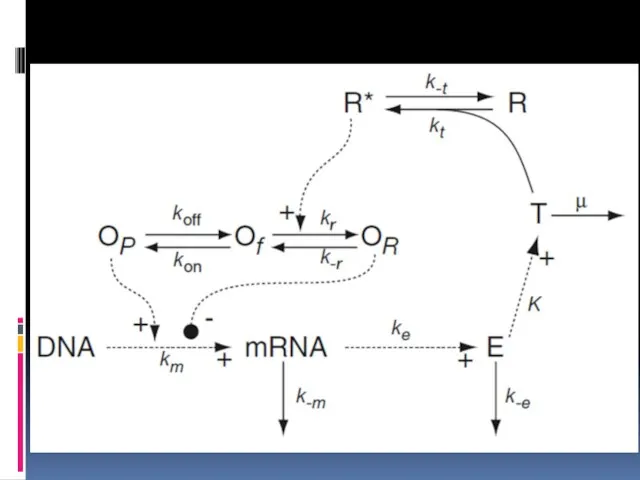
Messenger RNA (M)
Operon-polymerase
Operon- repressor
oP + of + oR = 1
activated repressor
Enzyme
Trp

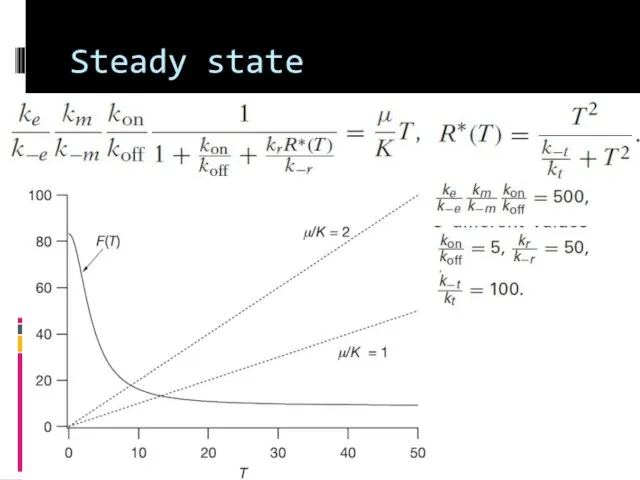
Steady state

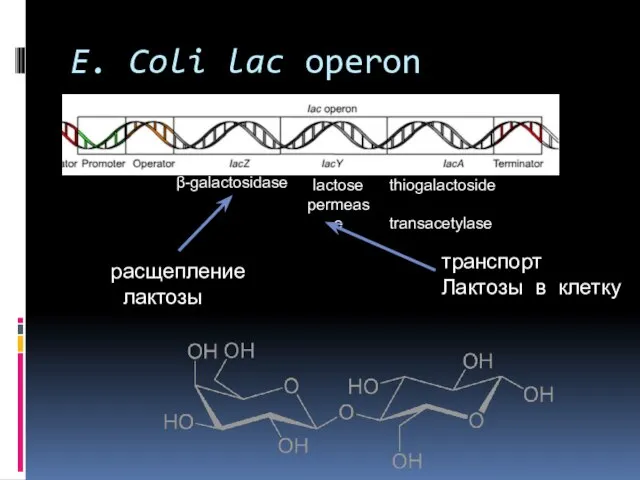
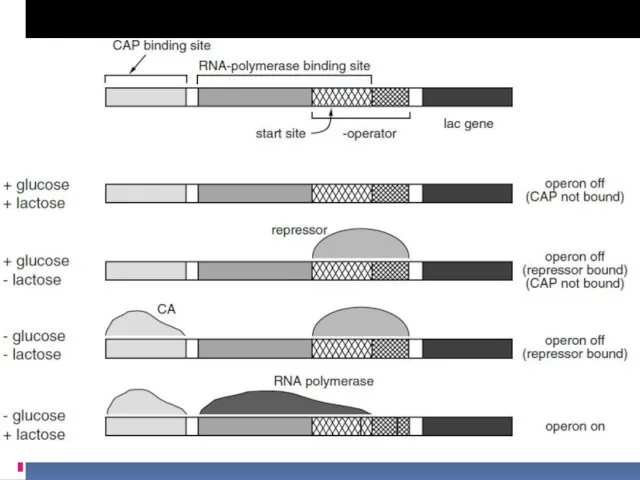
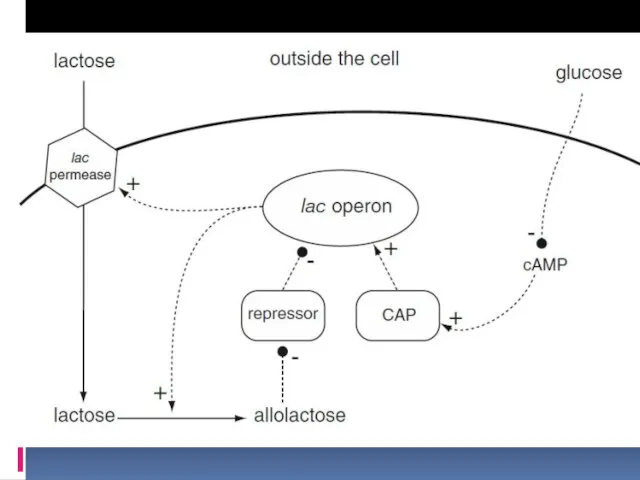
E. Coli lac operon
lactose
permease
β-galactosidase
thiogalactoside
transacetylase
расщепление
лактозы
транспорт
Лактозы в клетку

Allolactose (А), lactose (L), permease (P)
β-galactosidase (B), mRNA (M), repressor (R)
Operon-repressor (or), operon-producing (op)
Steady-state
Steady-state

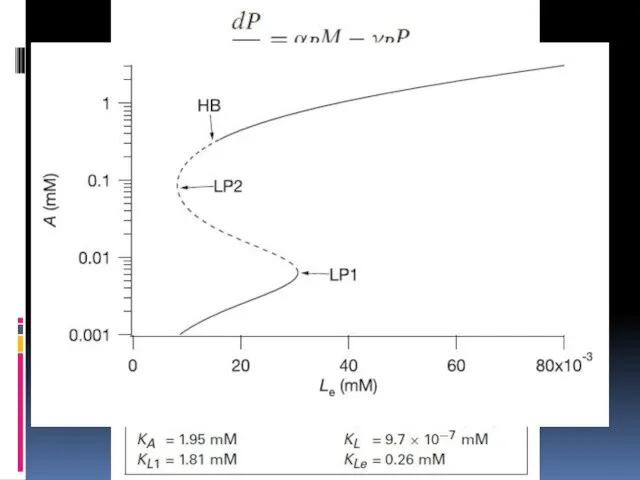
Триггер Жакоба-Мано

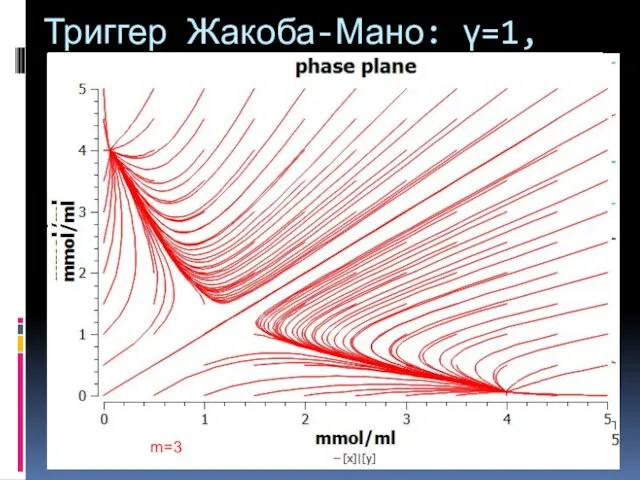
Триггер Жакоба-Мано: γ=1, L=4
m

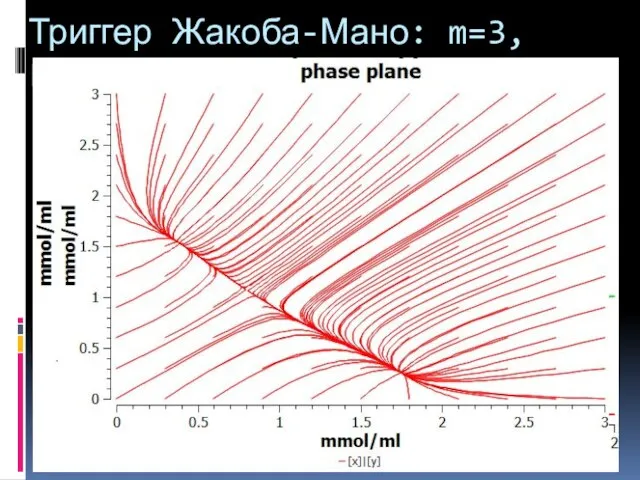
Триггер Жакоба-Мано: m=3, L=1.61
gamma

Предельный цикл
О1. Предельным циклом векторного поля на фазовой плоскости называется замкнутая (периодическая) траектория этого векторного поля, в окрестности которой нет других периодических траекторий.

Предельный цикл
С каждой из сторон предельный цикл является либо отталкивающим, либо притягивающим. Если поведение с обеих сторон одинаково — цикл называется соответственно отталкивающим или притягивающим. Если же с одной стороны происходит притяжение, а с другой отталкивание — говорят о полуустойчивом цикле

Теорема Пуанкаре-Бендиксона
О2. Предельное множество —это множество состояний, к которым объект неограниченно приближается при неограниченном возрастании (или убывании) времени.
Т1. Пусть задано C1-гладкое векторное поле на плоскости или в некоторой области плоскости, имеющее лишь конечное число особых точек. Тогда ω-предельное множество любой траектории — это либо (1) особая точка, либо (2) периодическая траектория, либо (3) полицикл (объединение особых точек и соединяющих их отрезков траекторий).

Теорема Пуанкаре-Бендиксона

Критерий Бендиксона
Если дивергенция векторного поля на плоскости знакопостоянна и отлична от нуля в некоторой односвязной области, то отсутствуют замкнутые фазовые кривые этого поля, целиком лежащие в этой области.

Бифуркации из пары комплексно-сопряженных λ: теорема Хопфа
Тогда в системе есть предельный цикл в области a0, причем радиус цикла пропорционален и частота близка к ω0
Цикл стабильный если ν > 0 и цикл существует при а > а0, либо если ν < 0 и цикл существует при а < а0. В противном случае он нестабильный.

Бифуркация Андронова-Хопфа
суперкритическая
бифуркация

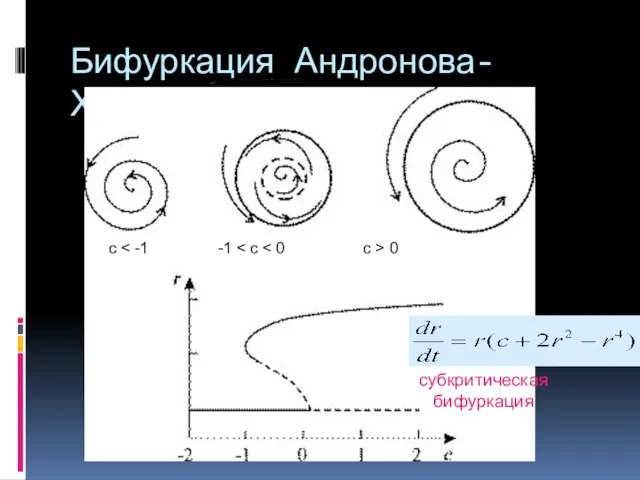
Бифуркация Андронова-Хопфа
субкритическая
бифуркация
с < -1 -1 < c < 0 c > 0

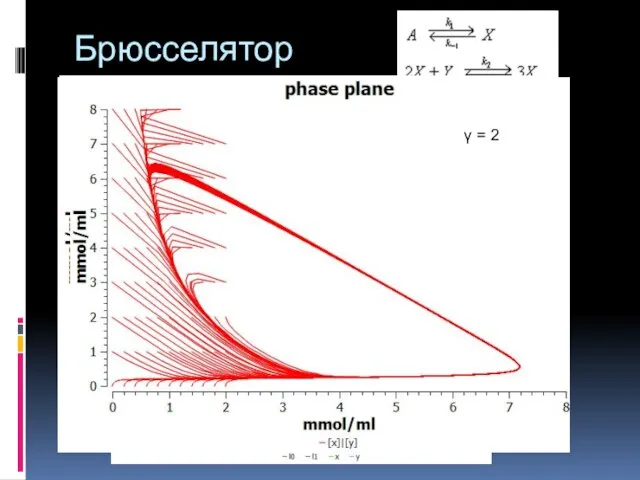
Брюсселятор

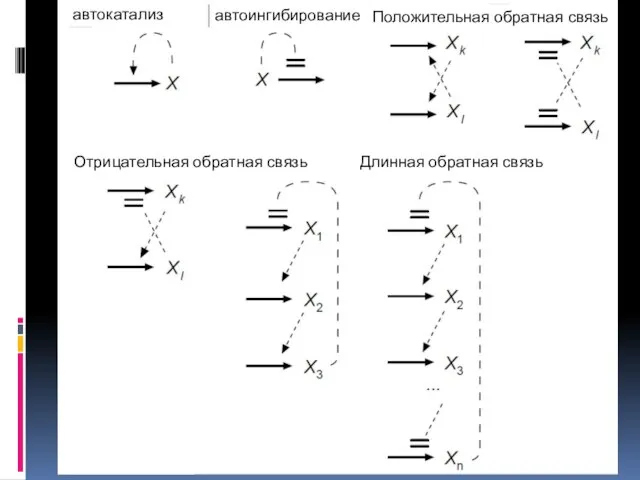
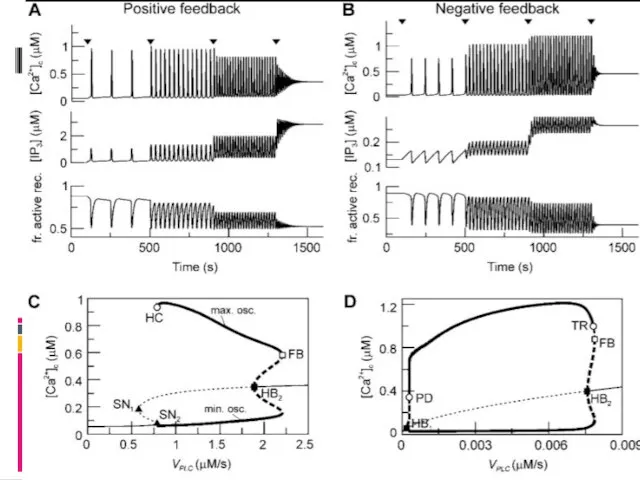
Я
автокатализ
автоингибирование
Положительная обратная связь
Отрицательная обратная связь
Длинная обратная связь

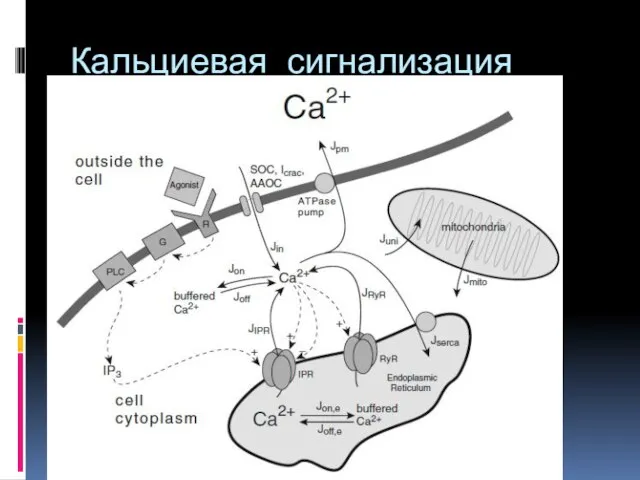
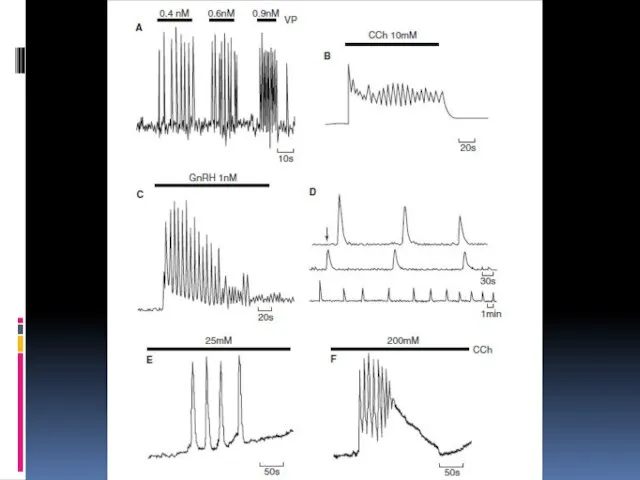
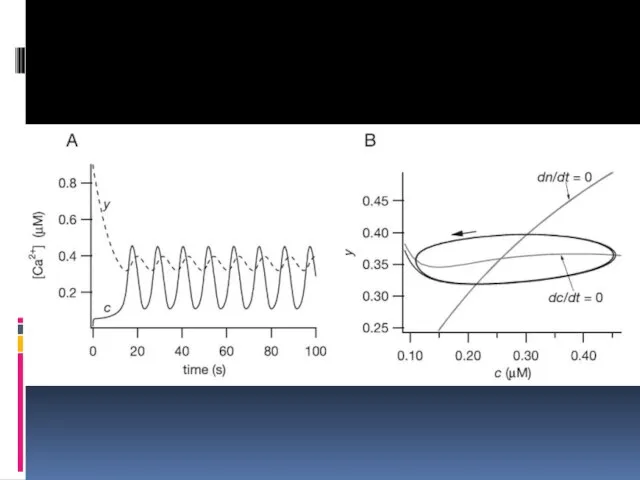
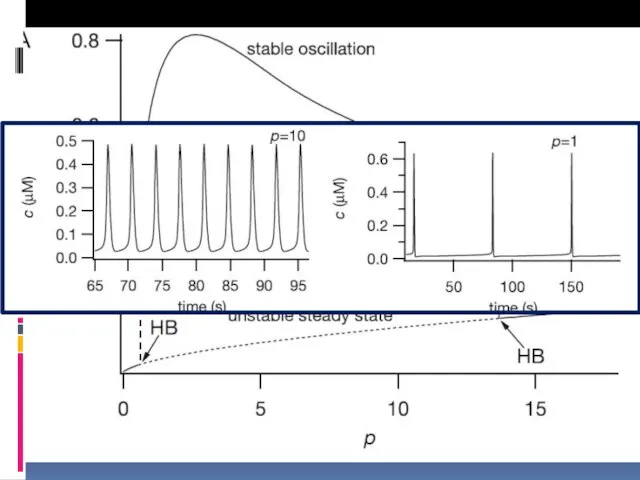
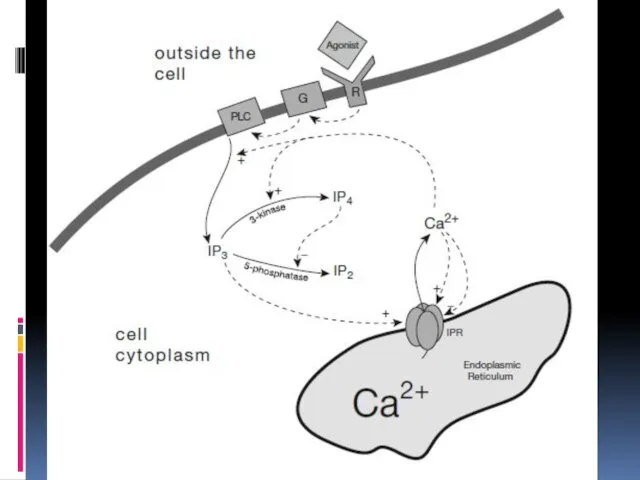
Кальциевая сигнализация

Открытая система

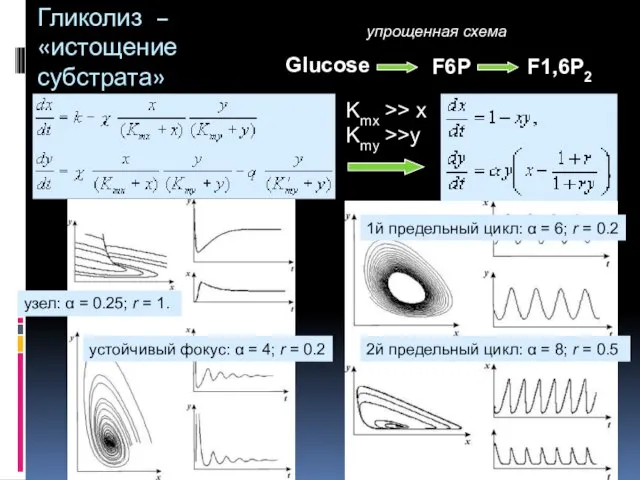
Гликолиз – «истощение субстрата»
Glucose
F6P
F1,6P2
упрощенная схема
Kmx >> x
Kmy >>y
узел: α = 0.25; r = 1.
устойчивый фокус: α = 4; r = 0.2
1й предельный цикл: α = 6; r = 0.2
2й предельный цикл: α = 8; r = 0.5

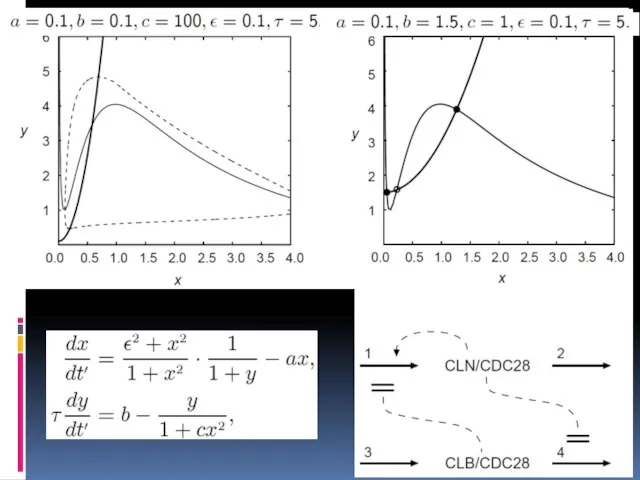
Циклины – «активатор-ингибитор»

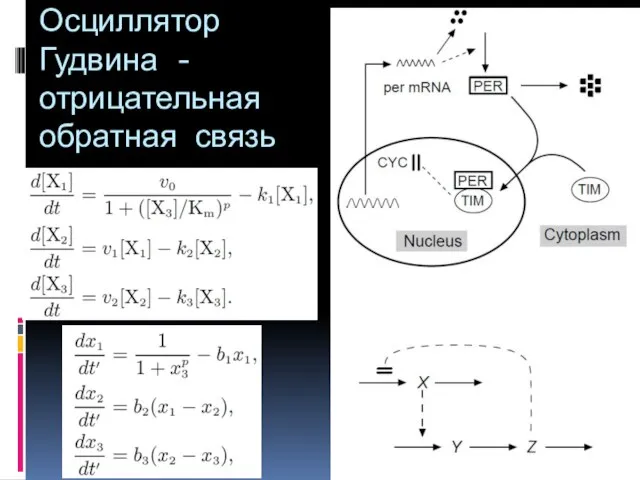
Осциллятор Гудвина - отрицательная обратная связь

Спасибо за внимание!