Содержание
- 2. ДИНАМИКА ПОПУЛЯЦИЙ МЕЖВИДОВЫЕ ВЗАИМОДЕЙСТВИЯ КОМПОНЕНТОВ БИОЦЕНОЗА МОДЕЛЬ ПРОГНОЗА И УПРАВЛЕНИЯ ДИНАМИКОЙ ПОПУЛЯЦИЙ Лекция 9 МОДЕЛИРОВАНИЕ ЭКОЛОГИЧЕСКИХ
- 3. ДИНАМИКА ПОПУЛЯЦИЙ Системная экология изучает популяции как самостоятельные подсистемы в рамках экологической системы, объединяющей их с
- 4. Например, разбив популяцию на группы самок и самцов, получают состав популяции. При этом структура популяции будет
- 5. Изменение плотности популяции происходит в результате взаимодействия четырех процессов: размножение, гибель, иммиграция, эмиграция X(tk+1) = X(tk)+(Vb–Vd)+(Vi–Ve)Δt,
- 6. Однако, количественное описание функций скорости иммиграции и эмиграции связано с необходимостью учета свойств не только данной,
- 7. Однако, количественное описание функций скорости иммиграции и эмиграции связано с необходимостью учета свойств не только данной,
- 8. В полевых условиях определить влияние процессов размножения и гибели на динамику популяций весьма затруднительно, X(tk+1) =
- 9. для независимой от плотности популяции компоненты r существует оптимальная комбинация факторов внешней и внутренней среды, при
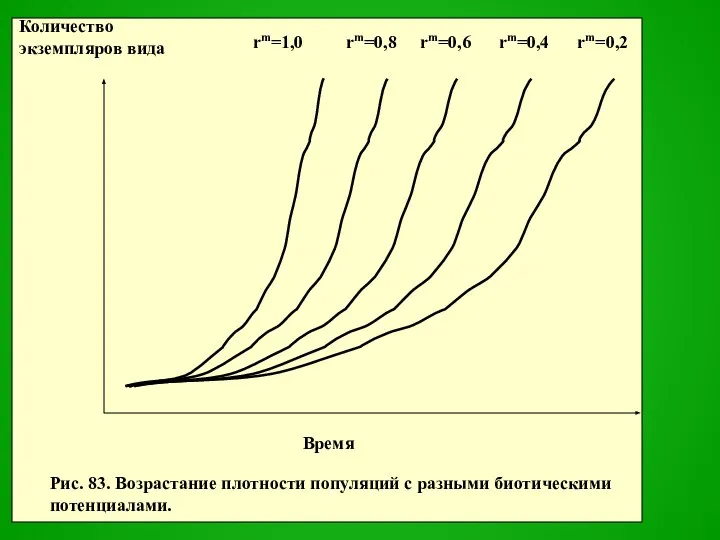
- 10. rm=1,0 rm=0,8 rm=0,6 rm=0,4 rm=0,2 Рис. 83. Возрастание плотности популяций с разными биотическими потенциалами.
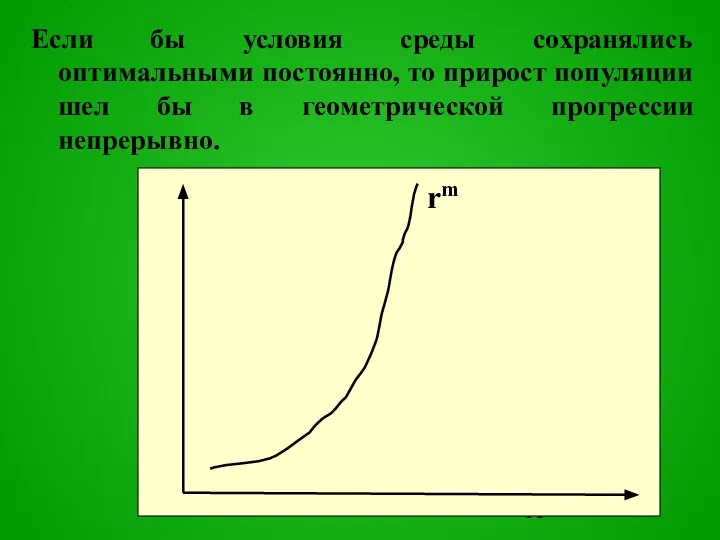
- 11. Если бы условия среды сохранялись оптимальными постоянно, то прирост популяции шел бы в геометрической прогрессии непрерывно.
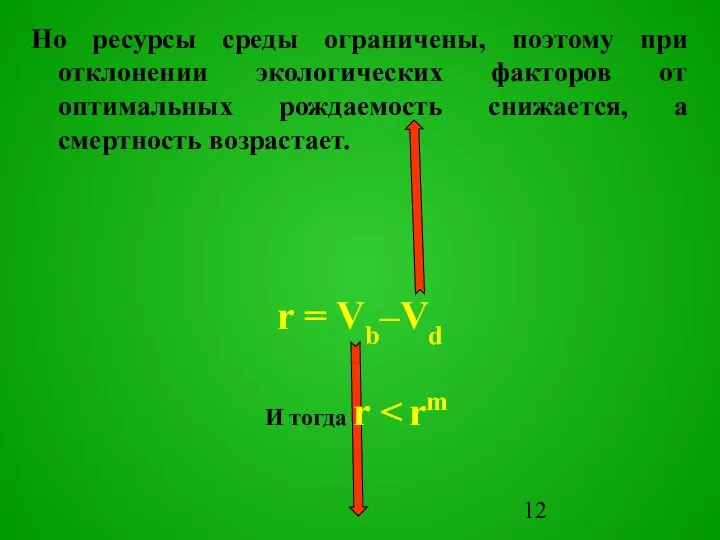
- 12. Но ресурсы среды ограничены, поэтому при отклонении экологических факторов от оптимальных рождаемость снижается, а смертность возрастает.
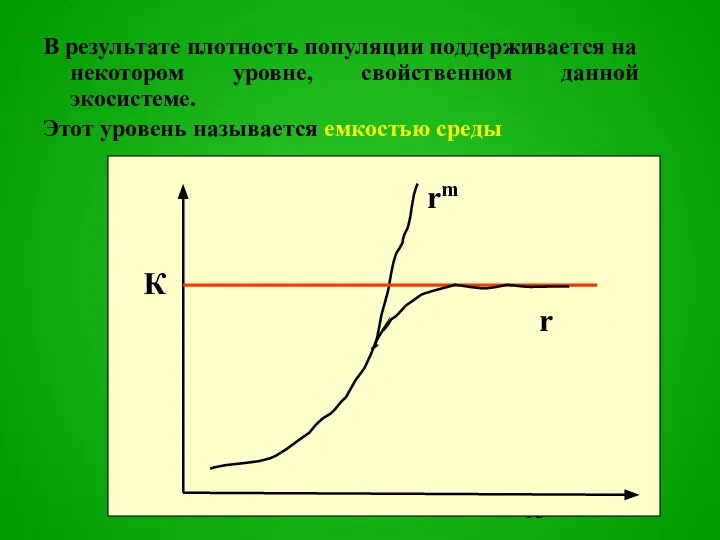
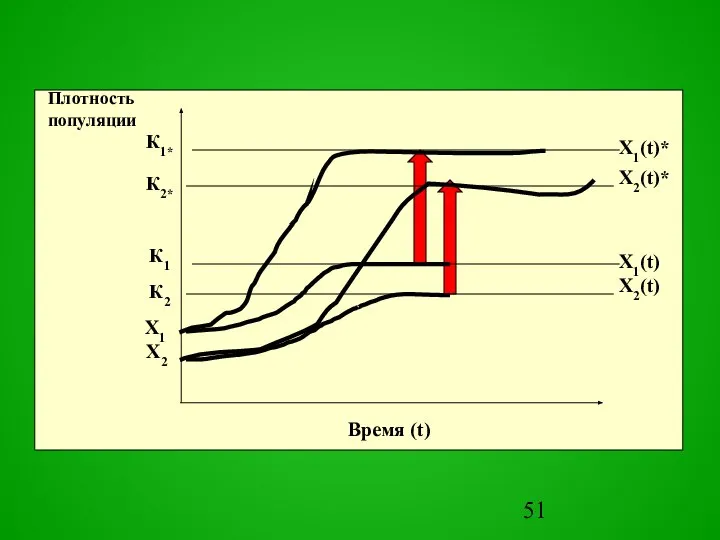
- 13. В результате плотность популяции поддерживается на некотором уровне, свойственном данной экосистеме. Этот уровень называется емкостью среды
- 14. Плотность популяции в среде с ограниченными ресурсами описывается уравнением, называемым логистическим K X(t1) = –––––––––––––––––––––––––––––, 1+(K–X(t0))/X(t0))
- 15. Для прогноза применить это уравнение можно, если предварительно выяснить зависимость Х от К при различном сочетании
- 16. В практике сельскохозяйственного производства агроном и консультант часто имеют дело с вредителями, болезнями и сорняками на
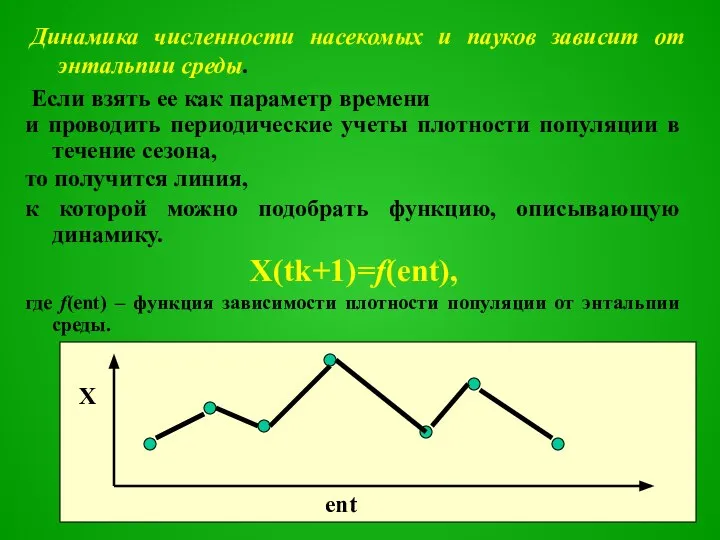
- 17. Динамика численности насекомых и пауков зависит от энтальпии среды. Если взять ее как параметр времени и
- 18. МЕЖВИДОВЫЕ ВЗАИМОДЕЙСТВИЯ КОМПОНЕНТОВ БИОЦЕНОЗА Прогноз динамики фитофагов гораздо точнее и реальнее, если ввести в него поправку
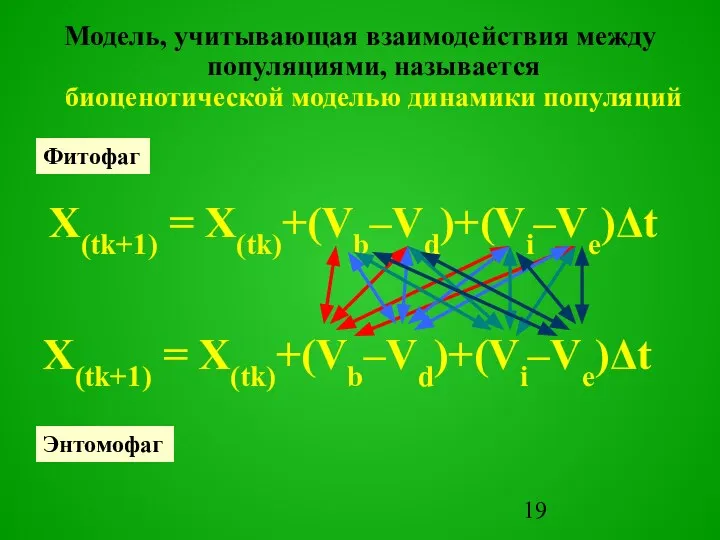
- 19. Модель, учитывающая взаимодействия между популяциями, называется биоценотической моделью динамики популяций X(tk+1) = X(tk)+(Vb–Vd)+(Vi–Ve)Δt Фитофаг Энтомофаг X(tk+1)
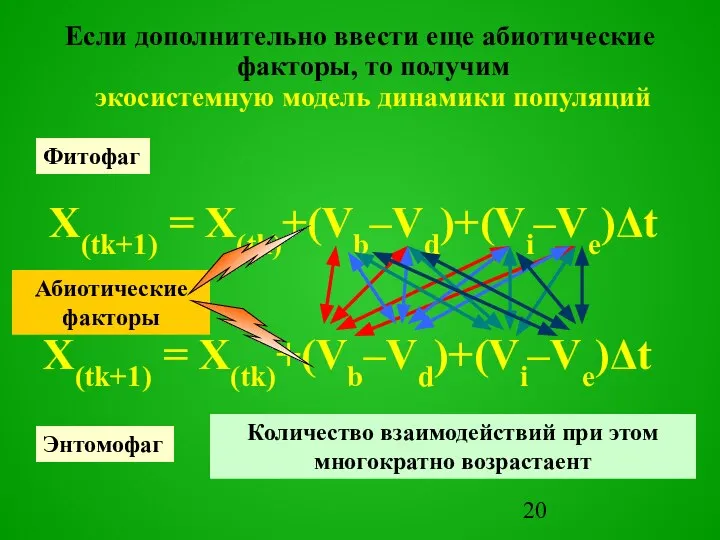
- 20. Если дополнительно ввести еще абиотические факторы, то получим экосистемную модель динамики популяций X(tk+1) = X(tk)+(Vb–Vd)+(Vi–Ve)Δt Фитофаг
- 21. Рождаемость (Vb) и смертность (Vd) зависят от многих факторов, основными из которых являются биотические взаимодействия. Последние
- 22. Частично преодолеть эти трудности оказалось возможным, когда взаимодействия стали классифицировать не по качественному разнообразию их механизмов,
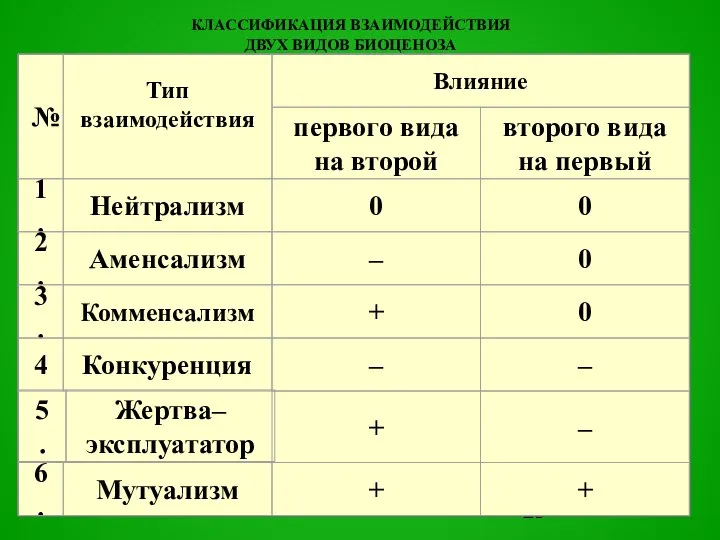
- 23. КЛАССИФИКАЦИЯ ВЗАИМОДЕЙСТВИЯ ДВУХ ВИДОВ БИОЦЕНОЗА
- 24. Популяции двух видов не оказывают непосредственного воздействия друг на друга. Нейтрализм (0, 0) 0 0 Такой
- 25. один из видов взаимодействующей пары в биоценозе оказывает отрицательное воздействие на рост другого, хотя сам не
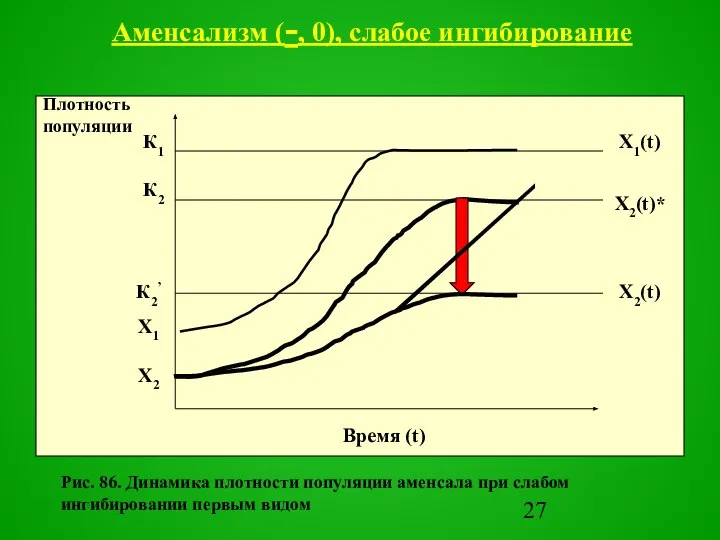
- 26. При слабом ингибировании система стремится к устойчивому стационарному состоянию, в котором численность аменсала будет меньше, чем
- 27. Рис. 86. Динамика плотности популяции аменсала при слабом ингибировании первым видом Аменсализм (-, 0), слабое ингибирование
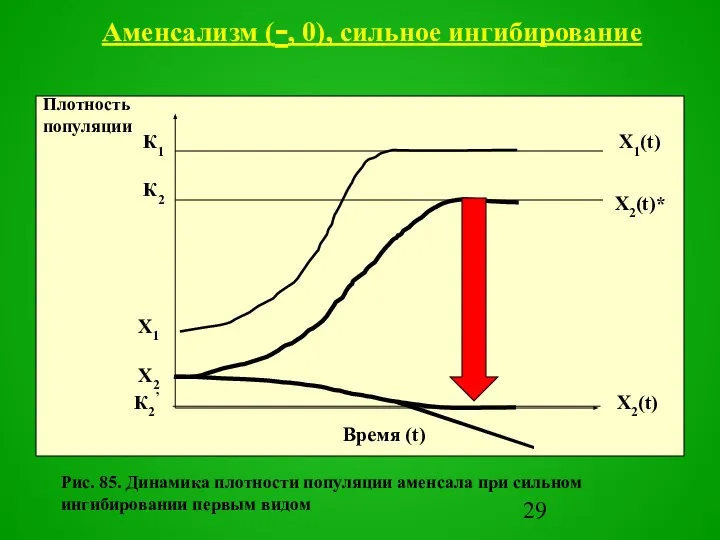
- 28. При сильном ингибировании популяция аменсала полностью погибает (элиминируется) Аменсализм (-, 0) сильное ингибирование
- 29. Рис. 85. Динамика плотности популяции аменсала при сильном ингибировании первым видом Аменсализм (-, 0), сильное ингибирование
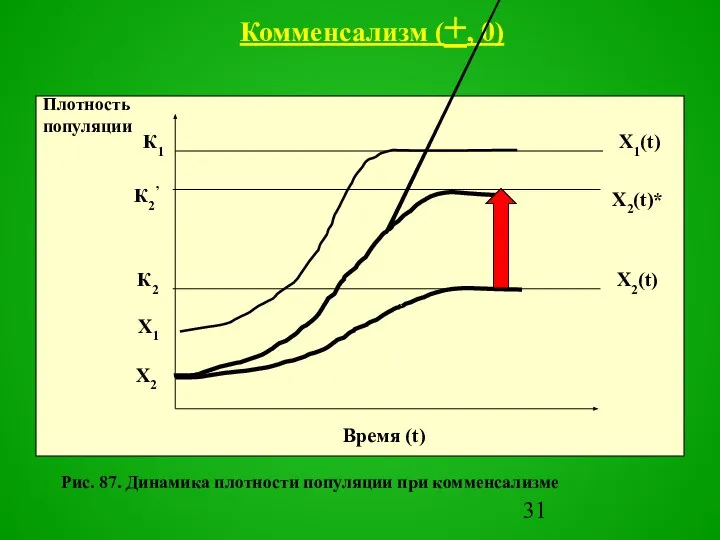
- 30. первый вид, называемый «хозяином», положительно воздействует на второй, называемый «комменсалом» («нахлебником»), а второй не влияет на
- 31. Рис. 87. Динамика плотности популяции при комменсализме Комменсализм (+, 0)
- 32. любое взаимно отрицательное отношение между видами. Конкуренция (интерференция (-, -) - - вид, получающий какое-либо преимущество
- 33. Частными случаями конкуренции являются: – конкуренция за тот или иной ограниченный ресурс (соперничество). Среди растений это
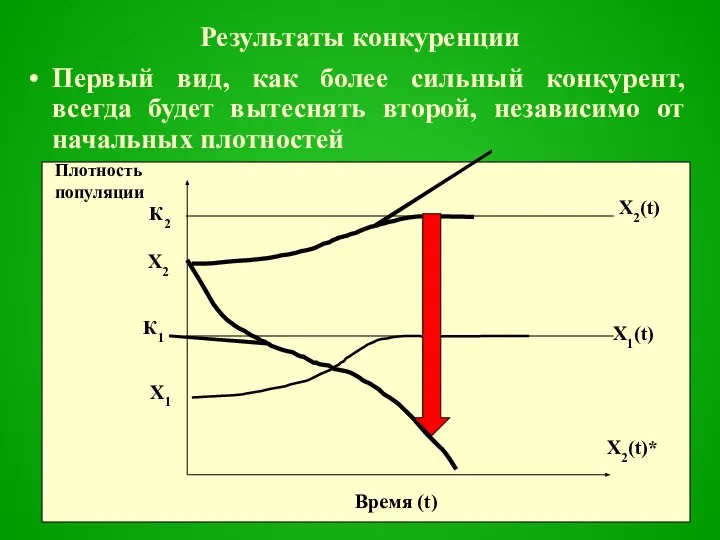
- 34. Результаты конкуренции Первый вид, как более сильный конкурент, всегда будет вытеснять второй, независимо от начальных плотностей
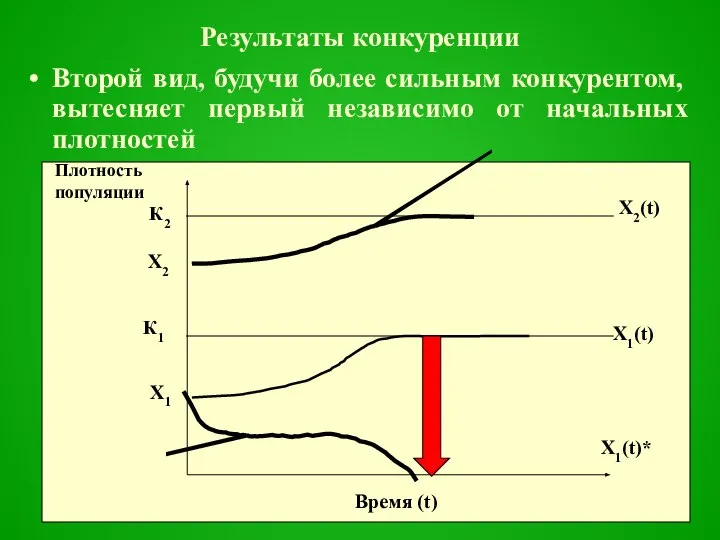
- 35. Результаты конкуренции Второй вид, будучи более сильным конкурентом, вытесняет первый независимо от начальных плотностей
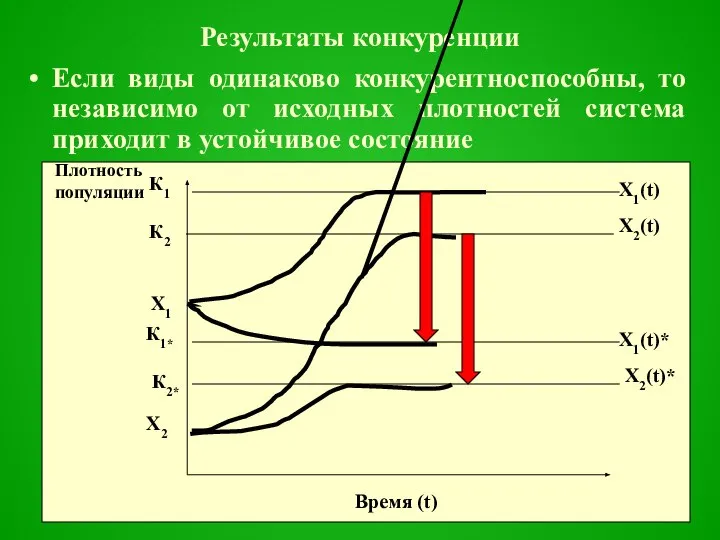
- 36. Результаты конкуренции Если виды одинаково конкурентноспособны, то независимо от исходных плотностей система приходит в устойчивое состояние
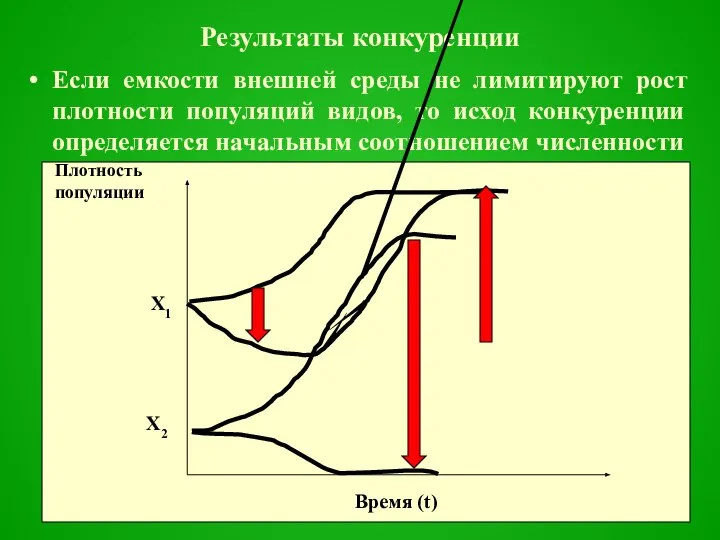
- 37. Результаты конкуренции Если емкости внешней среды не лимитируют рост плотности популяций видов, то исход конкуренции определяется
- 38. Таким образом, для обеспечения устойчивости конкурентного равновесия в системе, если оно возможно, достаточно, чтобы самоингибирование каждой
- 39. отношения между двумя видами, при которых увеличение (или уменьшение) плотности популяции первого («жертвы») влечет за собой
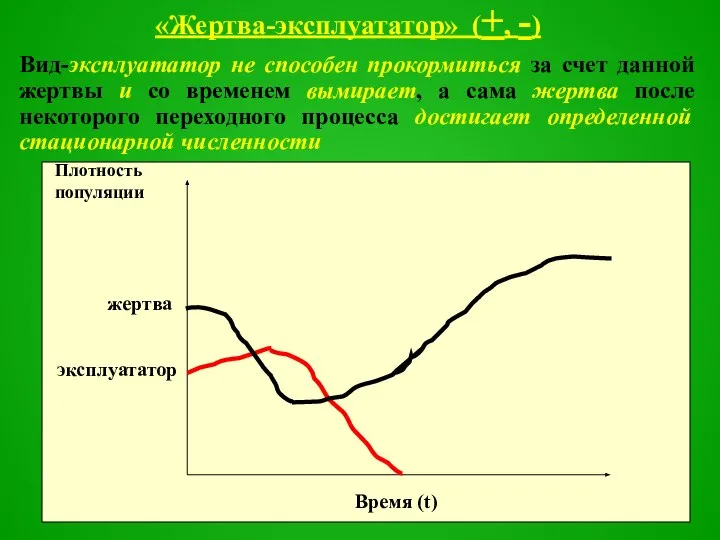
- 40. «Жертва-эксплуататор» (+, -) Вид-эксплуататор не способен прокормиться за счет данной жертвы и со временем вымирает, а
- 41. Типичный пример – применение биологического метода защиты растений, когда внедренный в экосистему хищник или паразит не
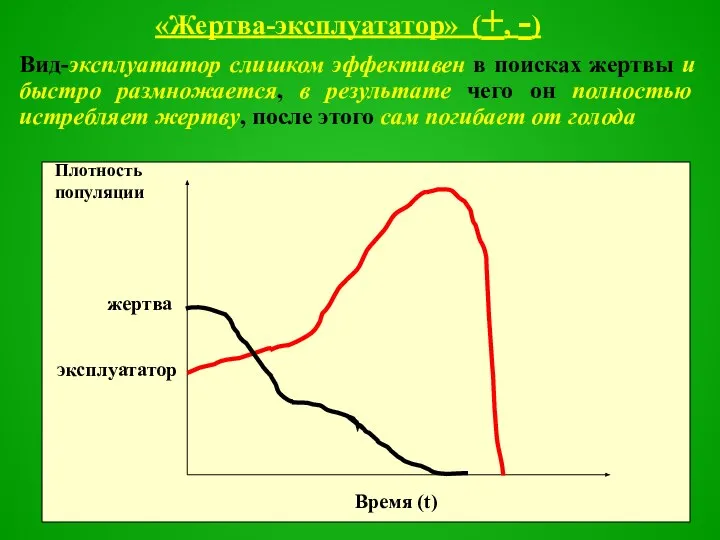
- 42. «Жертва-эксплуататор» (+, -) Вид-эксплуататор слишком эффективен в поисках жертвы и быстро размножается, в результате чего он
- 43. Ситуация “козел в огороде” характерна для монофагов, используемых как средство биологической защиты растений.
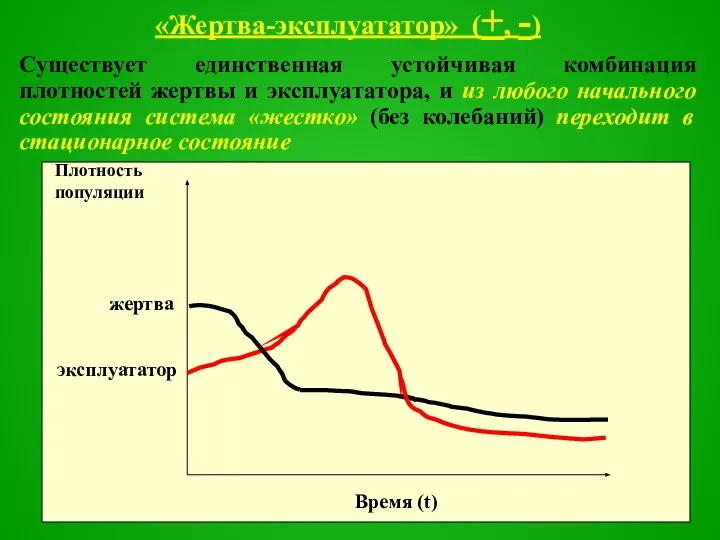
- 44. «Жертва-эксплуататор» (+, -) Существует единственная устойчивая комбинация плотностей жертвы и эксплуататора, и из любого начального состояния
- 45. Это ситуация, когда эксплуататор достаточно эффективен и может быстро снижать численность жертвы до низкого стационарного уровня,
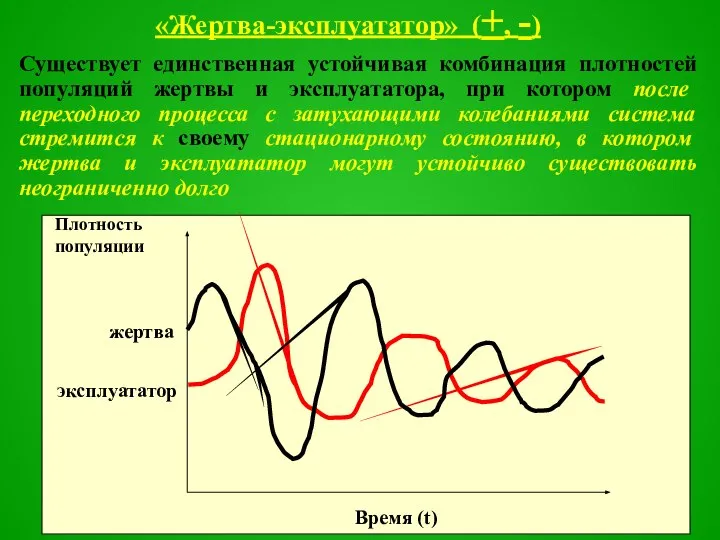
- 46. «Жертва-эксплуататор» (+, -) Существует единственная устойчивая комбинация плотностей популяций жертвы и эксплуататора, при котором после переходного
- 47. Например, взаимодействие растений и копытных растительноядных животных, которые периодически мигрируют на другие участки. В агроэкосистемах –
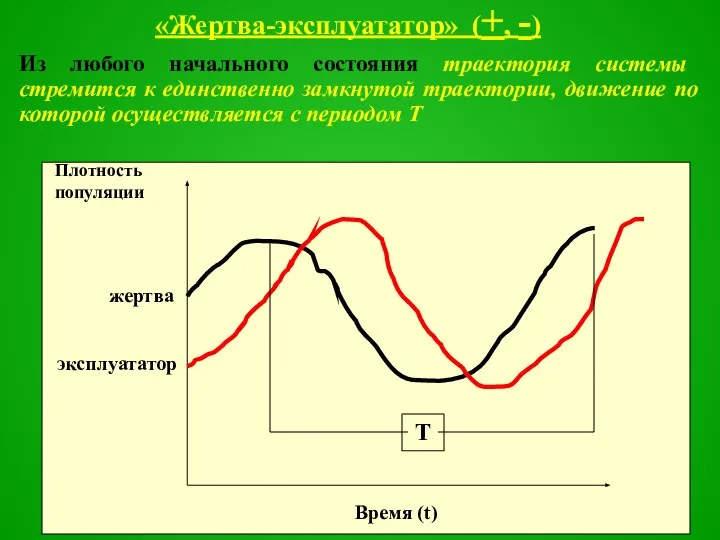
- 48. «Жертва-эксплуататор» (+, -) Из любого начального состояния траектория системы стремится к единственно замкнутой траектории, движение по
- 49. Такие автоколебания характерны для ненарушенных внешними факторами систем, где высокая степень саморегуляции. Синусоидальная траектория характеризует внутренне
- 50. взаимно положительное влияние, которое в конечном счете проявляется в том, что увеличение (снижение) численности любого из
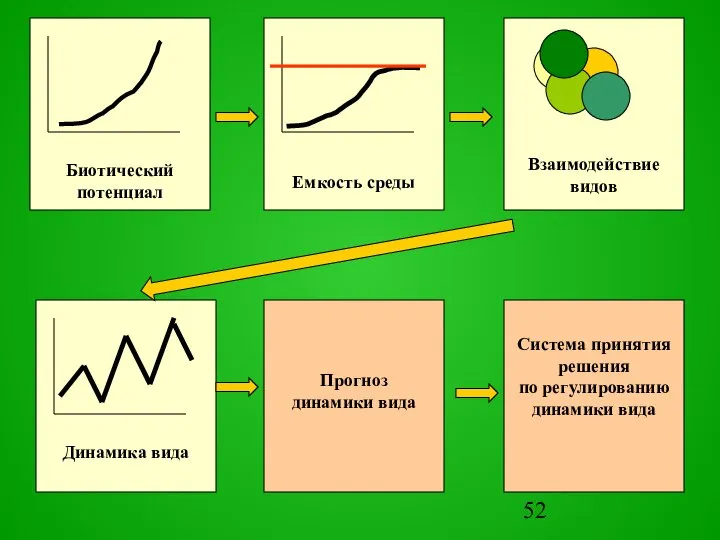
- 53. Все многообразие моделей прогнозов по шкале времени можно разделить на прогнозы МОДЕЛЬ ПРОГНОЗА И УПРАВЛЕНИЯ ДИНАМИКОЙ
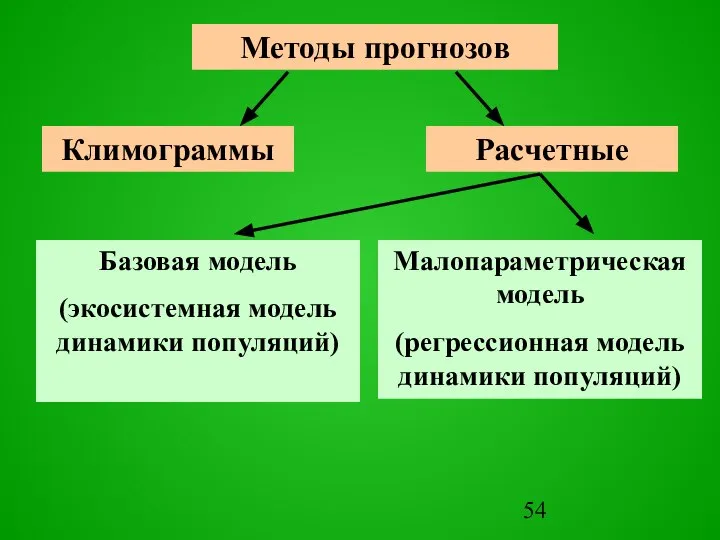
- 54. Методы прогнозов
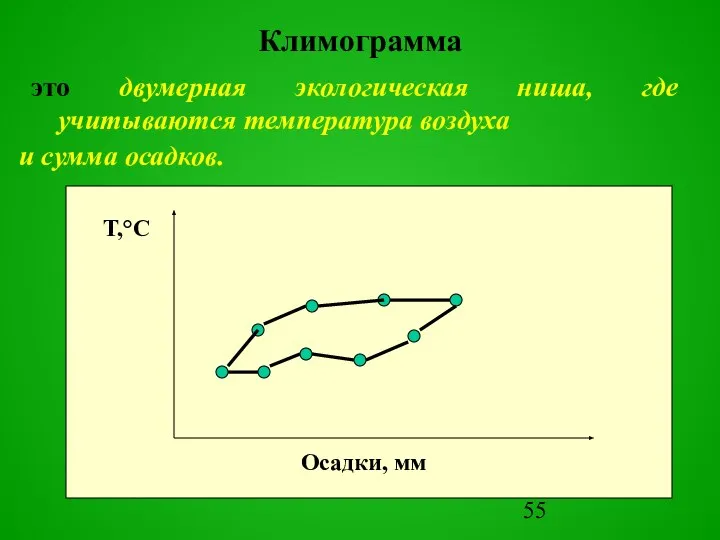
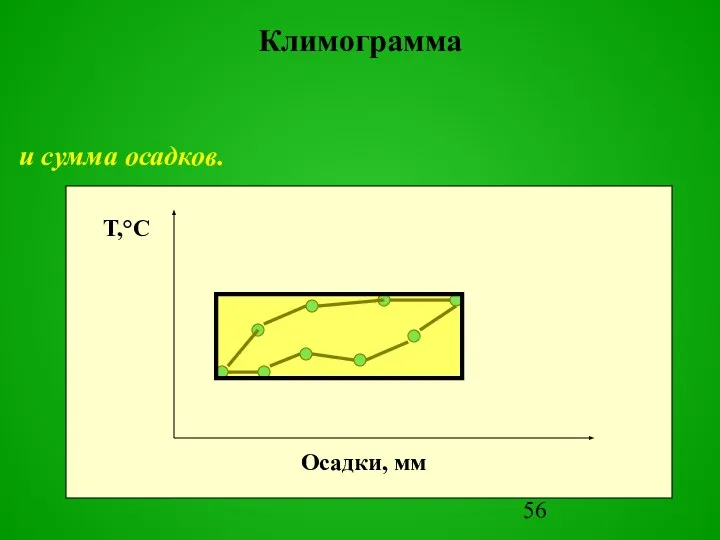
- 55. Климограмма это двумерная экологическая ниша, где учитываются температура воздуха
- 56. Климограмма
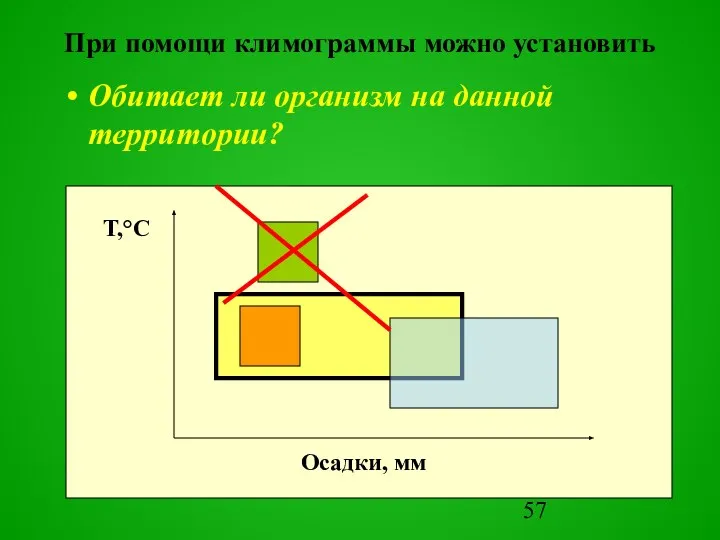
- 57. При помощи климограммы можно установить Обитает ли организм на данной территории? Осадки, мм
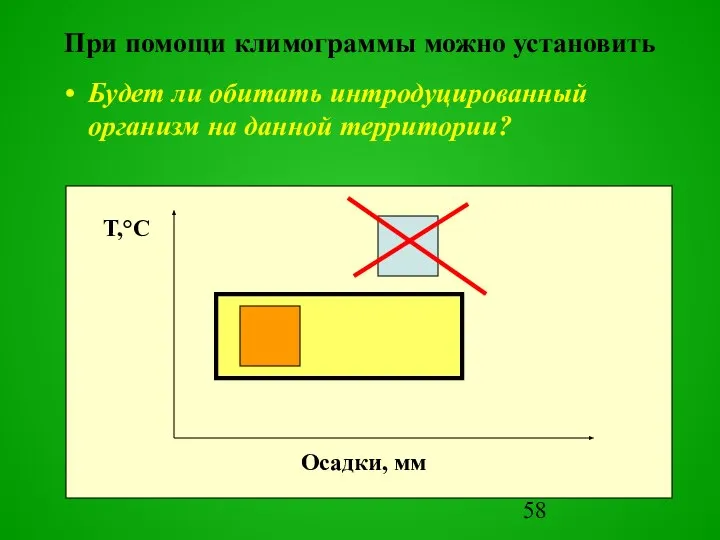
- 58. При помощи климограммы можно установить Будет ли обитать интродуцированный организм на данной территории? Осадки, мм
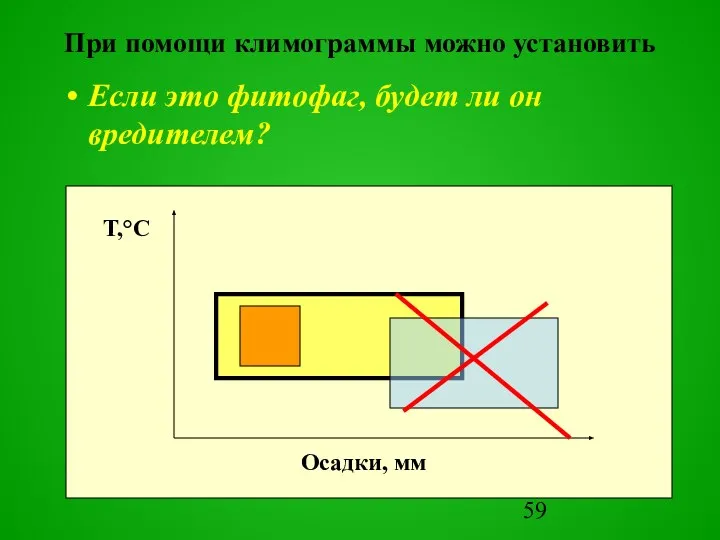
- 59. При помощи климограммы можно установить Если это фитофаг, будет ли он вредителем? Осадки, мм
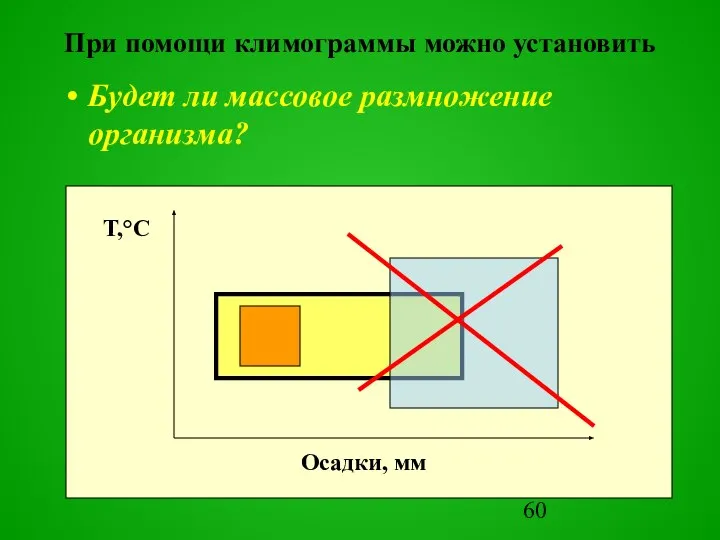
- 60. При помощи климограммы можно установить Будет ли массовое размножение организма? Осадки, мм
- 61. Например, размножение тлей зависит от метеорологических условий и фазы разввития растения. Низкие температуры и обильные частые
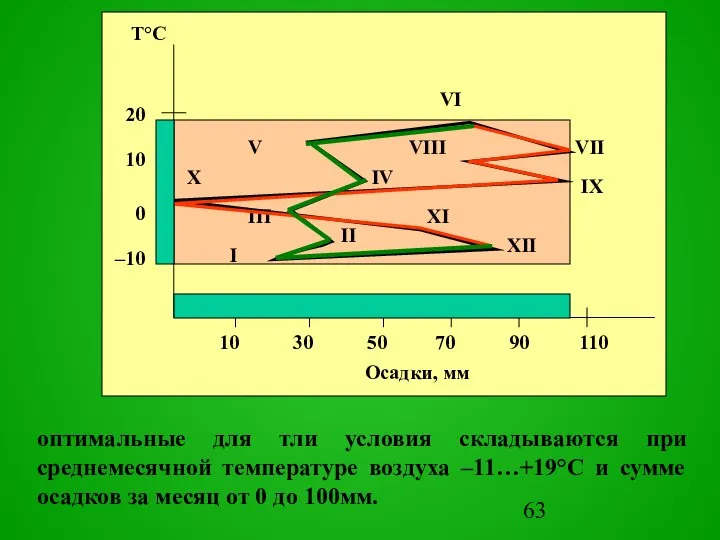
- 62. В 1988 году в Костромской области наблюдалось массовое размножение тли. Воспользовавшись этим обстоятельством, мы составили климограмму
- 63. оптимальные для тли условия складываются при среднемесячной температуре воздуха –11…+19°С и сумме осадков за месяц от
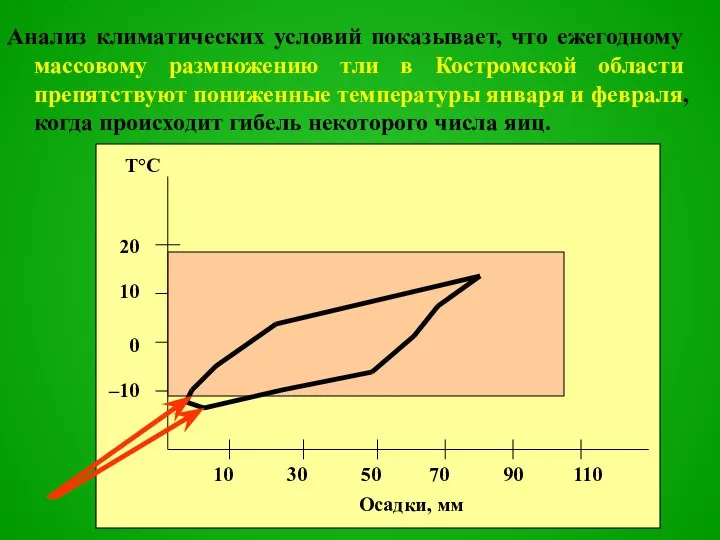
- 64. Анализ климатических условий показывает, что ежегодному массовому размножению тли в Костромской области препятствуют пониженные температуры января
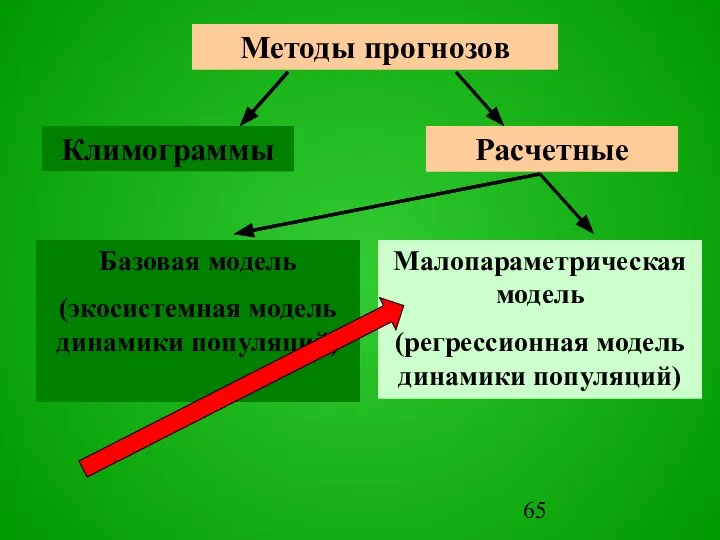
- 65. Методы прогнозов
- 66. Сезонный и оперативный прогнозы динамики составляются при помощи математических функций. Y=F(x) Для обеспечения возможности прогнозирования в
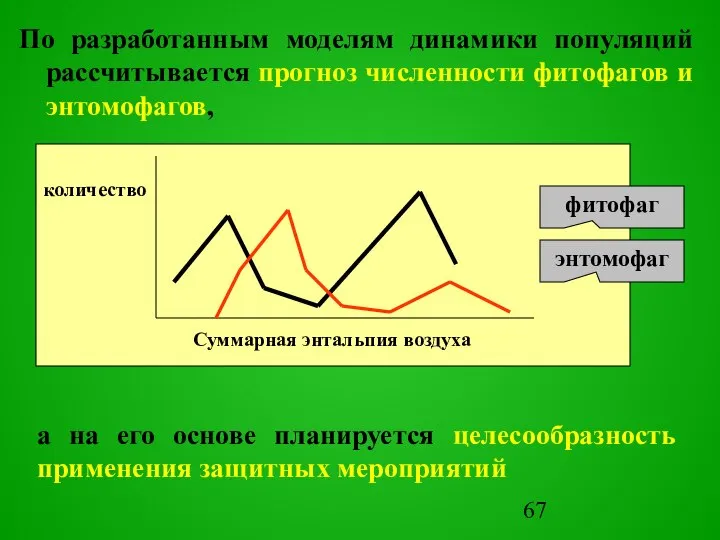
- 67. По разработанным моделям динамики популяций рассчитывается прогноз численности фитофагов и энтомофагов, количество Суммарная энтальпия воздуха а
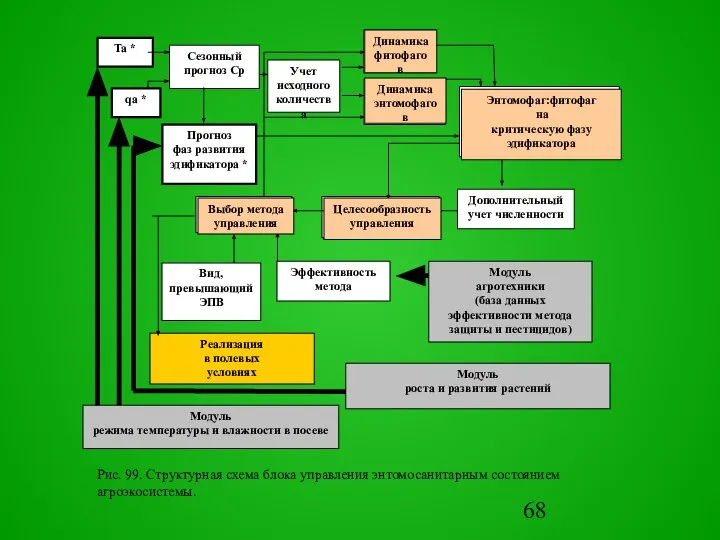
- 68. Ta * qa * Рис. 99. Структурная схема блока управления энтомосанитарным состоянием агроэкосистемы. Энтомофаг:фитофаг на критическую
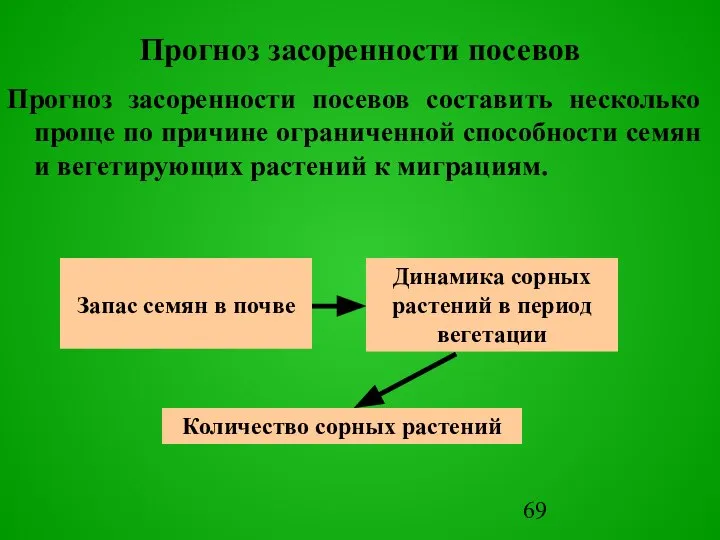
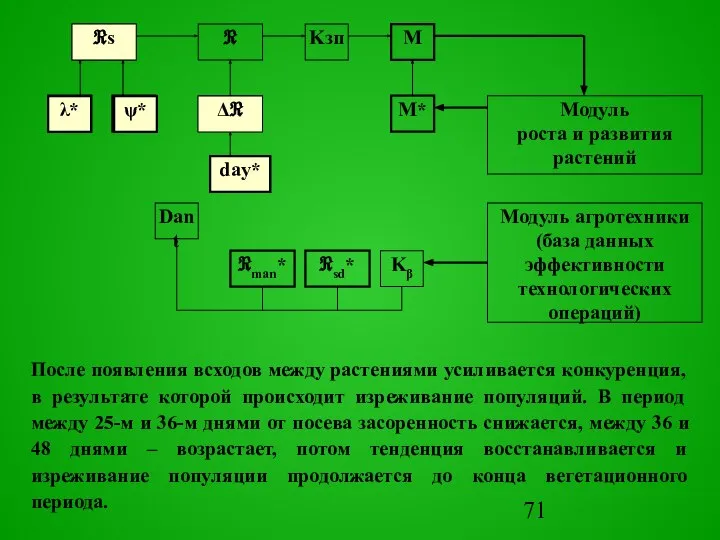
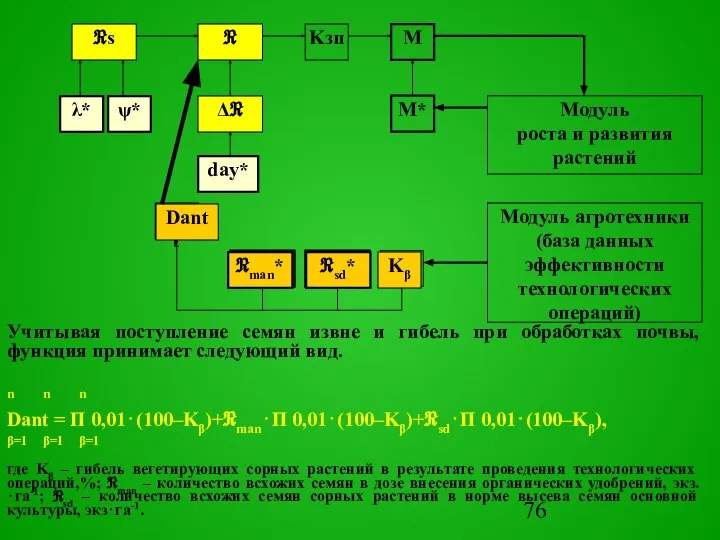
- 69. Прогноз засоренности посевов Прогноз засоренности посевов составить несколько проще по причине ограниченной способности семян и вегетирующих
- 70. М* М day* ψ* Kзп Модуль агротехники (база данных эффективности технологических операций) Модуль роста и развития
- 71. М* М day* ψ* Kзп Модуль агротехники (база данных эффективности технологических операций) Модуль роста и развития
- 72. М* М day* ψ* Kзп Модуль агротехники (база данных эффективности технологических операций) Модуль роста и развития
- 73. М* М Kзп Модуль агротехники (база данных эффективности технологических операций) Модуль роста и развития растений Dant
- 74. М* М Kзп Модуль агротехники (база данных эффективности технологических операций) Модуль роста и развития растений Dant
- 75. 20% 30% 80% 50%
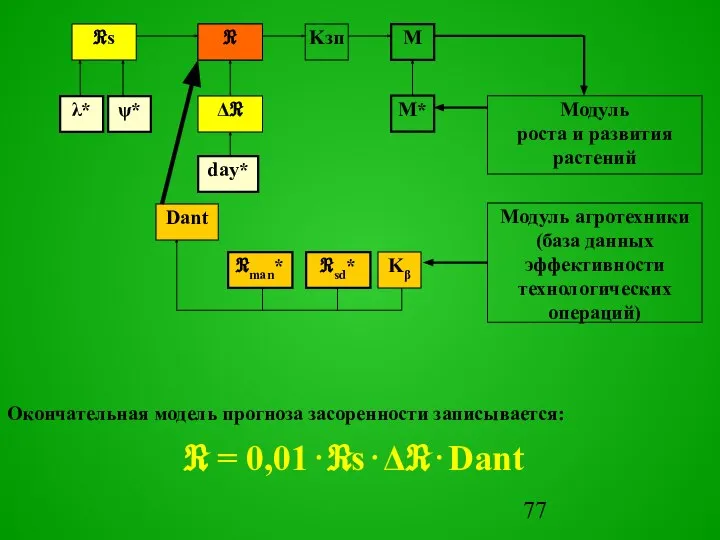
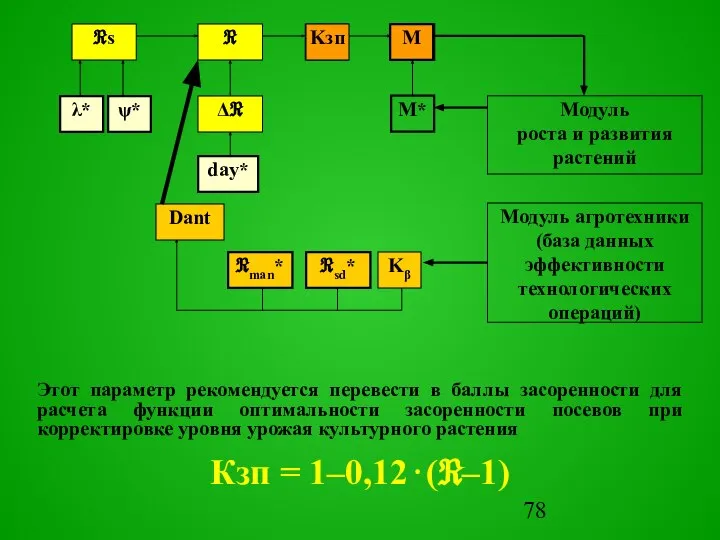
- 76. М* М Kзп Модуль агротехники (база данных эффективности технологических операций) Модуль роста и развития растений Dant
- 77. М* М Kзп Модуль агротехники (база данных эффективности технологических операций) Модуль роста и развития растений λ*
- 78. М* М Kзп Модуль агротехники (база данных эффективности технологических операций) Модуль роста и развития растений λ*
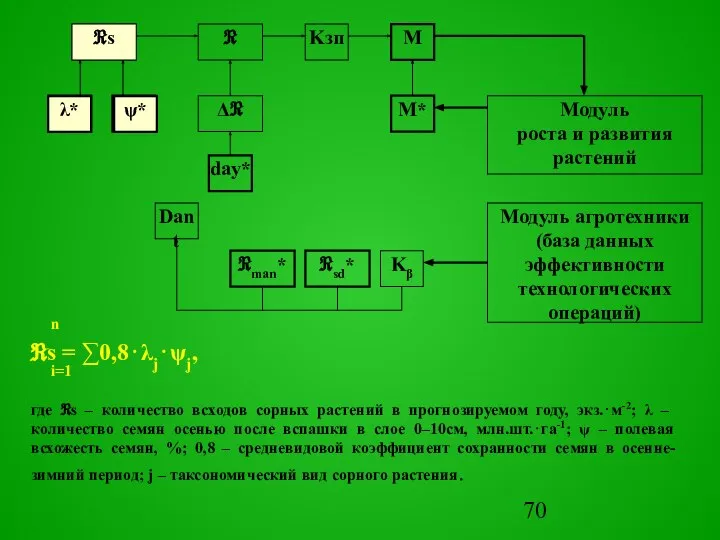
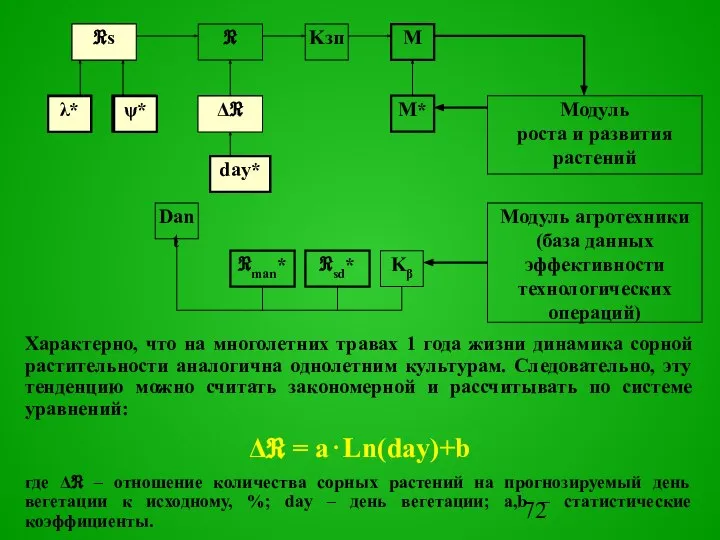
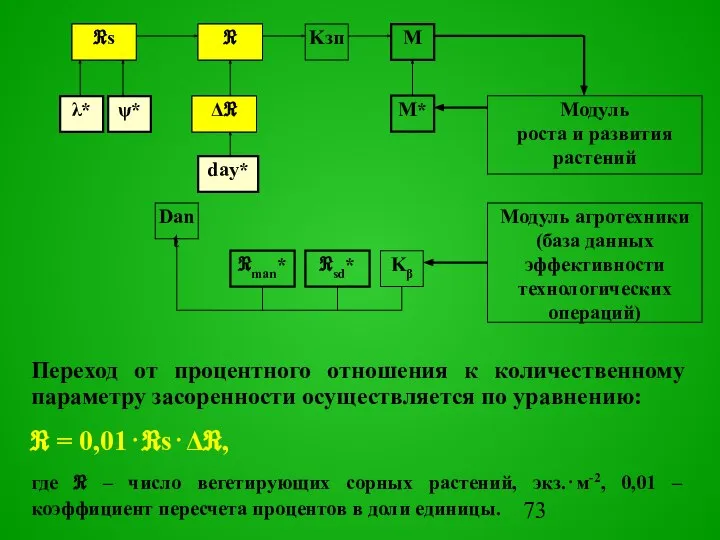
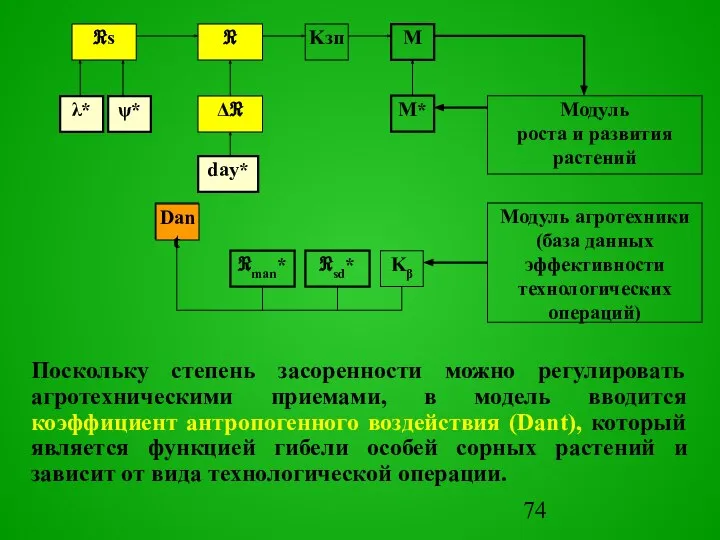
- 79. Тогда малопараметрическая модель прогноза урожайности с учетом засоренности посевов запишется в виде Y(Q,W,t,NPK,pH,Зп) = Y(Q,W,t,NPK,pH)⋅Кзп
- 81. Скачать презентацию



































 Эссе на тему экология
Эссе на тему экология Экологическое сообщество Муравейник
Экологическое сообщество Муравейник Основные экологические проблемы современности
Основные экологические проблемы современности Самостоятельная практическая работа в экологическом направлении
Самостоятельная практическая работа в экологическом направлении Биопосуда на пути решения экологических проблем
Биопосуда на пути решения экологических проблем Земля - хрупкая планета (часть 1)
Земля - хрупкая планета (часть 1) Расширенное заседание общественной палаты Санкт-Петербурга
Расширенное заседание общественной палаты Санкт-Петербурга Мы НЕ против храма. Мы ПРОТИВ застройки Малой земли и памятника природы Суджукская лагуна
Мы НЕ против храма. Мы ПРОТИВ застройки Малой земли и памятника природы Суджукская лагуна Птичья столовая. Кормушки для птиц
Птичья столовая. Кормушки для птиц Берегите природу: не выбрасывайте мусор и окурки на землю
Берегите природу: не выбрасывайте мусор и окурки на землю Экотимуровцы. Цени природу
Экотимуровцы. Цени природу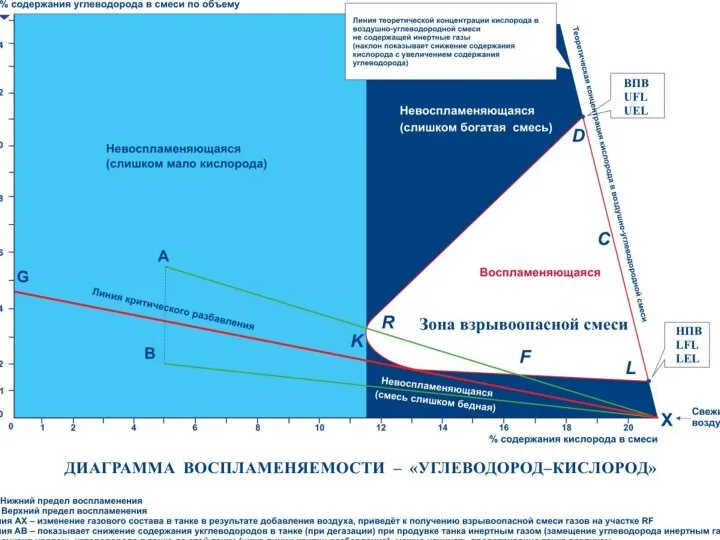 Диаграмма воспламеняемости
Диаграмма воспламеняемости Вторичная переработка мусора
Вторичная переработка мусора Стратегия популяризации раздельного сбора отходов в городе Севастополе
Стратегия популяризации раздельного сбора отходов в городе Севастополе 10- летие Сосновоборской общественной организации ЭХО
10- летие Сосновоборской общественной организации ЭХО Откуда в снежках грязь? 1 класс
Откуда в снежках грязь? 1 класс Участники водохозяйственного комплекса
Участники водохозяйственного комплекса Влияние деятельности человека на пресноводные водоёмы. Охрана водоёмов
Влияние деятельности человека на пресноводные водоёмы. Охрана водоёмов Открытая эколого- географическая игра Зеленое потребление природных ресурсов
Открытая эколого- географическая игра Зеленое потребление природных ресурсов Типы почв
Типы почв Эко-Тимуровцы
Эко-Тимуровцы Итоги деятельности Комитета по охране водных объектов Санкт-Петербурга в 2020 году
Итоги деятельности Комитета по охране водных объектов Санкт-Петербурга в 2020 году Обзор важнейших абиотических факторов среды. Механизмы адаптации
Обзор важнейших абиотических факторов среды. Механизмы адаптации Заповедные места России. Заповедные острова
Заповедные места России. Заповедные острова Эоловая деятельность
Эоловая деятельность Гимн поём мы молоку
Гимн поём мы молоку Команда ВГТУ. Промышленная экология
Команда ВГТУ. Промышленная экология Как можно сохранить природу?
Как можно сохранить природу?