Слайд 2Экономика. Часть 1. Микроэкономика
ПРОДОЛЖИТЕЛЬНОСТЬ: МОДУЛЬ 1
СЕМИНАРОВ - 7
КОНТРОЛЬНАЯ РАБОТА – 1
УЧЕБНИКИ
1.

Ким И. Микроэкономика.
М.: Юрайт. 2017
2. Корнейчук Б. Экономическая теория.
М.: Юрайт, 2021. Часть 1
biblio-online.ru
Слайд 3Формула оценивания
Итоговая оценка =
0,29·Оценка за контр. работу в части 1 +
0,11·Оценка за

работу на семинарах в части 1 +
0,29·Оценка за контр. работу в части 2 +
0,11·Оценка за работу на семинарах в части 2 +
0,2·Оценка за тесты (Москва)
Итог. оценка = 0,8·Оценка за практикум(СПб) +
0,2·Оценка за тесты (Москва)
(сверить с программой, возможны изменения)
Слайд 4МИКРОЭКОНОМИКА – РАЗДЕЛ ЭКОНОМИЧЕСКОЙ ТЕОРИИ, КОТОРЫЙ ИЗУЧАЕТ ПОВЕДЕНИЕ ОТДЕЛЬНЫХ ЭКОНОМИЧЕСКИХ СУБЪЕКТОВ:
• ПРОИЗВОДИТЕЛЕЙ

•ПРОДАВЦОВ
• ПОТРЕБИТЕЛЕЙ • ПОКУПАТЕЛЕЙ
• РАБОТНИКОВ • РАБОТОДАТЕЛЕЙ
• ФИРМ • ИНВЕСТОРОВ
• РЫНКОВ ТОВАРОВ
Слайд 5СУБЪЕКТЫ МИКРОЭКОНОМИКИ (1.1)
1. ДОМОХОЗЯЙСТВА
–владеют экон. ресурсами (факторами произ-водства) и получают доход

от их продажи:
КАПИТАЛ – созданные людьми средства производства, доход – ПРОЦЕНТ
ЗЕМЛЯ – природные ресурсы, доход – РЕНТА
ТРУД – способности человека (рабочая сила и человеческий капитал), доход – ЗАРПЛАТА
ПРЕДПРИНИМАТЕЛЬСКАЯ СПОСОБНОСТЬ – умение комбинировать капитал, труд и землю для создания товаров; доход – ПРИБЫЛЬ
Слайд 62. ФИРМА
− покупает экон. ресурсы, производит и продает продукты с целью

максимизации прибыли
БИЗНЕС – сфера деятельности фирм
ПРЕДПРИНИМАТЕЛЬ – одновременно владелец фирмы (получает прибыль) и домохозяйство (владеет факторами и покупает продукты).
ПРИБЫЛЬ (π) – разность выручки и издержек:
π = TR – TC
ВЫРУЧКА (TR) – произведение цены (р) и объема проданного товара (Q):
TR = p·Q
ИЗДЕРЖКИ (TC) – затраты на покупку экономических ресурсов, материалов и др.
Слайд 8ЭФФЕКТИВНОСТЬ (1.2)
– соотношение результата и затрат
1.СРЕДНЯЯ ПРОИЗВОДИТЕЛЬНОСТЬ ТРУДА (АР)
АР = ВЫПУСК

ПРОДУКТА : ЗАТРАТЫ ТРУДА
• АРА = 5 дет./ч, АРВ = 4 дет./ч. ⇒ АРА > АРВ
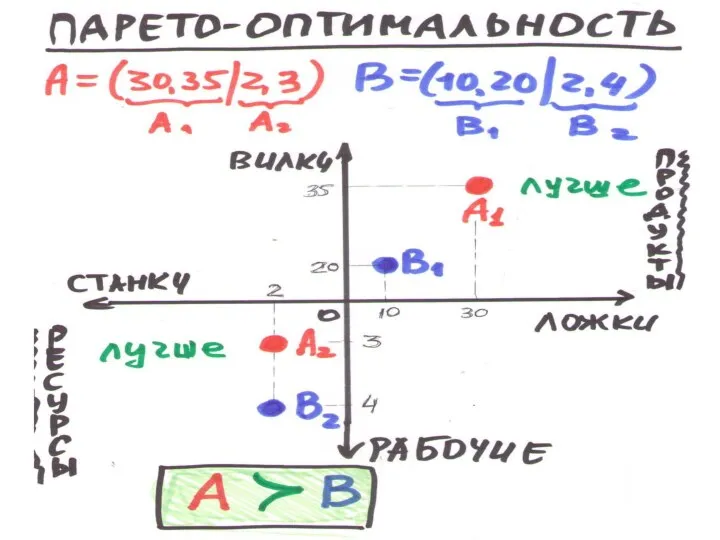
2.ПАРЕТО–эффективность: каждый выпуск (слева от |) не меньше, каждые затраты не больше
• SA = (4, 5, 8, | 13, 14)
SB = (5, 7, 8, | 11, 12) ⇒ SA ‹ SB сравнимы
• SA = (4, 5, 9, | 13, 14)
SB = (5, 7, 8, | 11, 12) ⇒ SA ? SB не сравнимы
Слайд 10ОТНОСИТЕЛЬНОЕ (ПРОЦЕНТНОЕ) ИЗМЕНЕНИЕ ПОКАЗАТЕЛЯ Y :
%∆Y = (новое Y : старое Y

– 1)·100%
%∆Y = (∆Y : старое Y)·100%
ПРИМЕР:
СТАРОЕ ЗНАЧЕНИЕ = 150
НОВОЕ ЗНАЧЕНИЕ = 120
%∆Y = (120/150 – 1)·100% = - 20%
ПОКАЗАТЕЛЬ УМЕНЬШИЛСЯ
Слайд 11ИНДЕКС (I)
- отношение нового и старого значений
ПРАВИЛО: Если А=В·С, то IА =

IВ·IС
ДОКАЖЕМ: TR1 = p1Q1, TR2 = p2Q2
Ip = p2/p1, IQ = Q2/Q1, ITR = TR2/TR1
ITR = (p2Q2)/(p1Q1) = (p2/p1)·(Q2/Q1) = Ip·IQ
ЗАДАЧА. p↑20%, Q↓20%. Найти %ΔTR
РЕШЕНИЕ. Ip =1,2, IQ =0,8 → ITR =1,2×0,8=0,96
%ΔTR =(ITR - 1)×100% =(0,96 - 1)·100% = -4%
Слайд 12 СПРОС И ПРЕДЛОЖЕНИЕ (2.1)
СПРОС
ИНДИВИДУАЛЬНЫЙ СПРОС d(p) – количество товара, которое

желает и способен купить покупатель по цене p за данный период времени
РЫНОЧНЫЙ СПРОС D(p) – количество товара, которое желают и способны купить все покупатели по цене p за данный период времени:
D(p) = d1(p) +…+ dn(p) = Σ di(p)
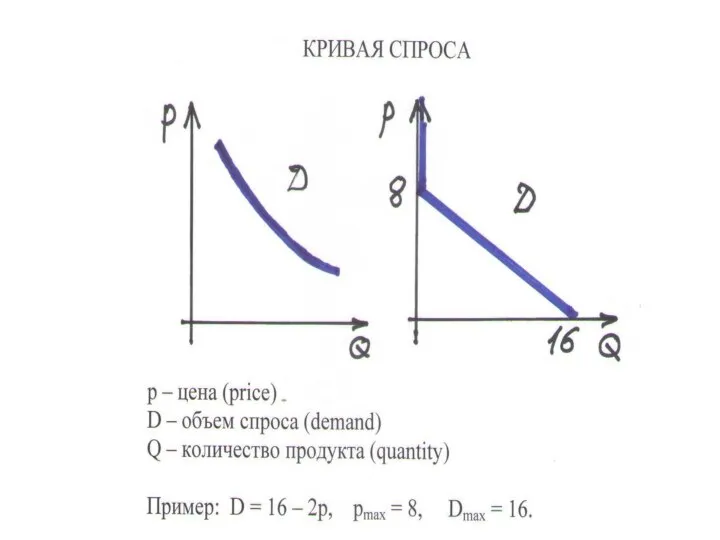
КРИВАЯ РЫНОЧНОГО СПРОСА – график D(p)
ПРИМЕР. D = 160 – 2p. Если р > 80, то D = 0, поэтому 80 – максимальная цена спроса
Слайд 14ЗАКОН СПРОСА:
• с ростом цены объем спроса падает:
р ↑ → D

↓
• функция D убывает • кривая D нисходящая
ЦЕНОВЫЕ ФАКТОРЫ СПРОСА – причины, определяющие форму кривой спроса:
• ЭФФЕКТ ЗАМЕЩЕНИЯ – с ростом цены растет потребление заменителей товара, которые стали относительно дешевле, поэтому потребление данного товара снижается
• ЭФФЕКТ ДОХОДА – с ростом цены снижается покупательная способность дохода , человек беднеет и сокращает потребление большинства товаров, в том числе данного
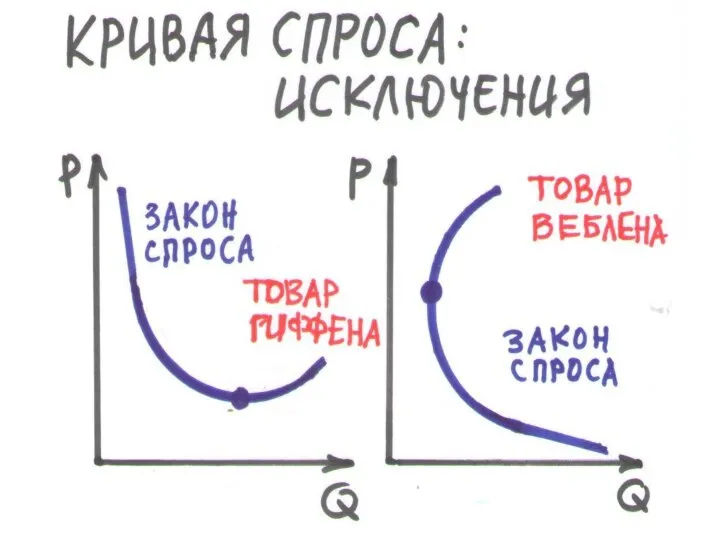
Слайд 15ИСКЛЮЧЕНИЯ ИЗ ЗАКОНА СПРОСА (2.5)
ТОВАР ГИФФЕНА – основной продукт потребления бедняков, не

имеющий заменителей. Спрос на него растет с ростом цены, т.к. эффект дохода действует в обратном направлении: с ростом цены потребитель беднеет, отказывается от качественных товаров и увеличивает спрос на товар (хлеб)
ТОВАР ВЕБЛЕНА – товар демонстративного потребления богачей, его ценность и спрос растут с ценой. Поведение богача нельзя объяснить с помощью эффектов замещения и дохода, т.к. его доход можно считать неограниченным
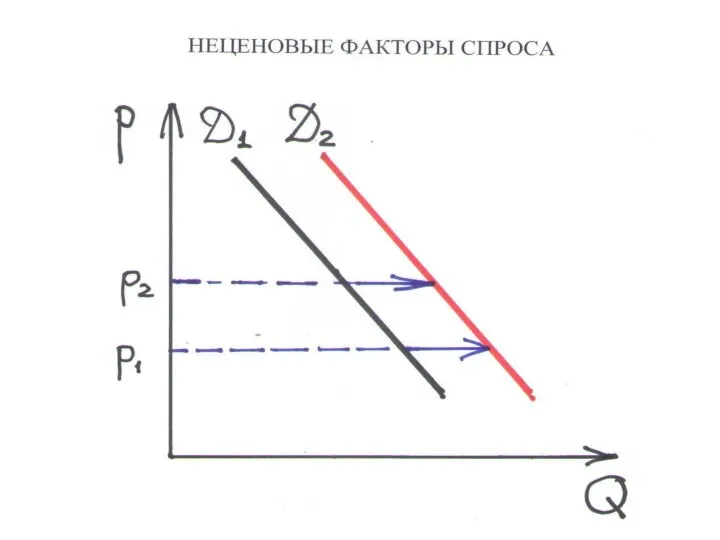
Слайд 17НЕЦЕНОВЫЕ ФАКТОРЫ СПРОСА
– причины изменение объема спроса при каждой цене, т.е.

сдвига кривой спроса:
ИЗМЕНЕНИЕ ДОХОДА. Увеличение дохода обычно сдвигает кривую спроса вправо
ИЗМЕНЕНИЕ ЦЕН ЗАМЕНИТЕЛЕЙ. Если заменители дорожают, то потребители «переключаются» на данный товар и спрос на него растет.
ИЗМЕНЕНИЕ ВКУСОВ. Реклама сдвигает кривую спроса вправо, антиреклама – влево.
ИНФЛЯЦИОННЫЕ ОЖИДАНИЯ. Ожидание роста цен побуждает закупать товар впрок и спрос растет.
ИЗМЕНЕНИЕ НАЛОГА НА ДОХОД. Увеличение подоходного налога (НДФЛ) снижает чистый доход, человек беднеет и снижает и спрос
Слайд 19ЭЛАСТИЧНОСТЬ СПРОСА (2.7)
1. ЦЕНОВАЯ ЭЛАСТИЧНОСТЬ СПРОСА – отношение относительного изменения спроса к

относительному изменению цены, умноженное на -1
Ed = – %ΔD:%Δp = – (ΔD/D):(Δp/p)
• определяется замещаемостью товара
• положительна, т.к. ΔD и Δp имеют разные знаки
• равна %-му снижению спроса при росте цены на 1%
Спрос называют:
Неэластичный при Ed < 1 (соль, спички)
Единично-эластичный при Ed = 1 (алкоголь)
Эластичный при Ed > 1 (торт «Весенний»)
Абсолютно эластичный при Ed = ∞ (паспорт)
Абсолютно неэластичным при Ed = 0 (инсулин)
Слайд 22ВЫЧИСЛЕНИЕ ЭЛАСТИЧНОСТИ
ПО ОПРЕДЕЛЕНИЮ. Эластичность при цене р1 :
Ed = - p1(D2 –

D1) : D1(p2 – p1)
D1 и D2 – спрос при цене p1 и p2
Недостаток: зависит от p2
ТОЧЕЧНАЯ ЭЛАСТИЧНОСТЬ: Ed = - p·D':D
Недостаток: нужно знать функцию D(p)
ДУГОВАЯ ЭЛАСТИЧНОСТЬ:
Ed = - (p1 + p2)(Q2 – Q1) : (Q1 + Q2)(p2 – p1)
Недостаток: зависит от двух цен
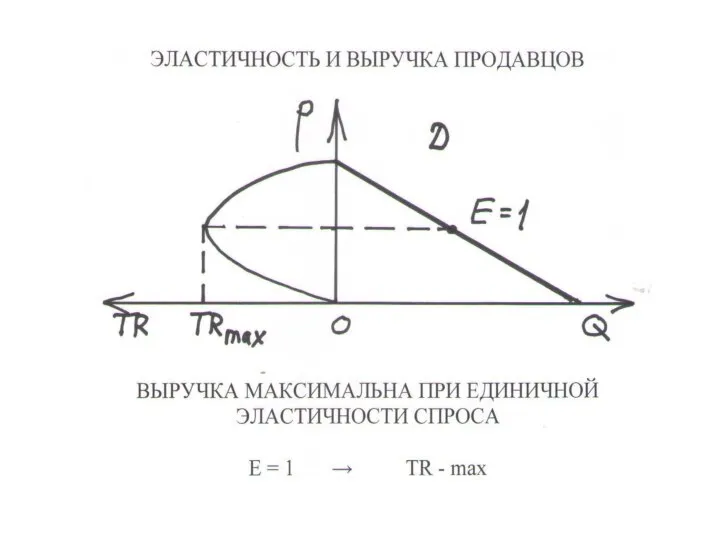
Слайд 23ВЫРУЧКА ПРОДАВЦОВ И ЭЛАСТИЧНОСТЬ
ВЫРУЧКА ПРОДАВЦОВ – стоимость товара,
который продадут на рынке при

данной цене:
TR(p) = p·D(p)
• равна площади прямоугольника с вершиной на кривой спроса
Исследуем производную TR:
TR' = 1·p + p·D' = D(1+pD'/D) = D(1 – Ed)
ВЫВОД: Выручка продавцов
• максимальна при Ed = 1
• растет с ростом р при неэласт. спросе (Ed < 1)
• снижается с ростом р при эласт. спросе (Ed > 1)
Слайд 25ЗАДАЧА О МАКСИМАЛЬНОЙ ВЫРУЧКЕ
ДАНО: Кривая спроса линейна, даны 2 точки
p1 =1, D1

=10; p2 =3, D2 =6. НАЙТИ TRmax
(p – p1) : (D – D1) = (p2 – p1) : (D2 – D1)
1) (p – 1) : (D – 10) = (3 – 1) : (6 – 10)
р = 6 – 0,5D – функция спроса (обратная)
2) TR = pD = (6 – 0,5D)D = 6D – 0,5D2
3) TR' = 6 – D = 0 → D = 6
4) TRmax = TR(6) = 6×6 – 0,5×62 = 18
Слайд 262. ЭЛАСТИЧНОСТЬ СПРОСА ПО ДОХОДУ
– отношение %-го изменения спроса к %-му

изменению дохода (i) при неизменной цене:
Ei = ΔD/D : Δi/i
• определяется доступностью товара
• больше 0, меньше 0, или равна 0
• равна % изменения спроса при росте дохода на 1%
Товар называют:
НОРМАЛЬНЫЙ при Ei > 0 (чай, икра)
ТОВАР 1-й НЕОБХОДИМОСТИ: 0 < Ei < 1 (чай)
ТОВАР 2-го УРОВНЯ (роскоши) при Ei > 1 (икра)
НЕКАЧЕСТВЕННЫЙ (инфериорный): Ei < 0 (маргарин)
Слайд 273. ПЕРЕКРЕСТНАЯ ЭЛАСТИЧНОСТЬ СПРОСА
– отношение %-го изменения спроса на товар X

к %-му изменению цены товара Y:
EXY = ΔDX/DX : ΔpY/pY
• определяется замещаемостью/дополняемостью X и Y
• может быть положительной и отрицательной
• % изменение спроса на X при росте цены Y на 1%
ВЗАИМОЗАМЕНЯЕМЫЕ ТОВАРЫ ( СУБСТИТУТЫ): EXY > 0 (свинина – говядина)
ВЗАИМОДОПОЛНЯЕМЫЕ ТОВАРЫ (КОМПЛЕМЕНТЫ):
EXY < 0 (авто – бензин)
НЕСОПРЯЖЕННЫЕ ТОВАРЫ (нейтральные): E XY = 0
(соль – спички)
Слайд 28ЗАДАЧА О ПЕРЕКРЕСТНОЙ ЭЛАСТИЧНОСТИ
Функция спроса: Qx = 5 – 2px+ 0,1py
НАЙТИ

Exy , если px = 2, py = 10
Exy = (ΔQx/Qx):(Δpy/py) = (py/Qx)∙(ΔQx/Δpy)
ΔQx/Δpy = 0,1
Exy = py ∙ 0,1/(5 – 2px + 0,1py)
Exy(2,10) = 10 ∙ 0,1/(5 – 2∙2 + 0,1∙10)
Exy(2,10) = 0,5 > 0
ВЫВОД: Товары – субституты
Слайд 29ПРЕДЛОЖЕНИЕ (2.1)
ИНДИВИДУАЛЬНОЕ ПРЕДЛОЖЕНИЕ s(p) – количество товара, которое желает и способен продать

продавец по цене p за данный период времени
РЫНОЧНОЕ ПРЕДЛОЖЕНИЕ S(p) – количество товара, которое желают и способны продать все продавцы по цене p за данный период времени
ЦЕНОВАЯ ЭЛАСТИЧНОСТЬ ПРЕДЛОЖЕНИЯ–отношение %-го изменения предложения к %-му изменению цены
ЗАКОН ПРЕДЛОЖЕНИЯ – с ростом цены объем предложения растет. Кривая S(p) – восходящая
ОБОСНОВАНИЕ: с ростом цены растет 1) число производителей, которые могут покрыть издержки, 2) выручка производителя
Слайд 30НЕЦЕНОВЫЕ ФАКТОРЫ ПРЕДЛОЖЕНИЯ
– причины изменения предложения при каждой цене, т.е. сдвига кривой

предложения:
1. ИЗДЕРЖКИ ПРОИЗВОДСТВА. Их рост вызывает сдвиг кривой предложения влево (влево-вверх, вверх). Причины роста издержек:
• рост цен на сырье и зарплаты рабочих
• снижение эффективности управления
• износ оборудования.
2. ЧИСЛО ПРОДАВЦОВ. Его увеличение вызывает сдвиг кривой предложения вправо-вниз
3. СУБСИДИИ И НАЛОГИ. Увеличение субсидии сдвигает кривую S вниз, акциза – вверх
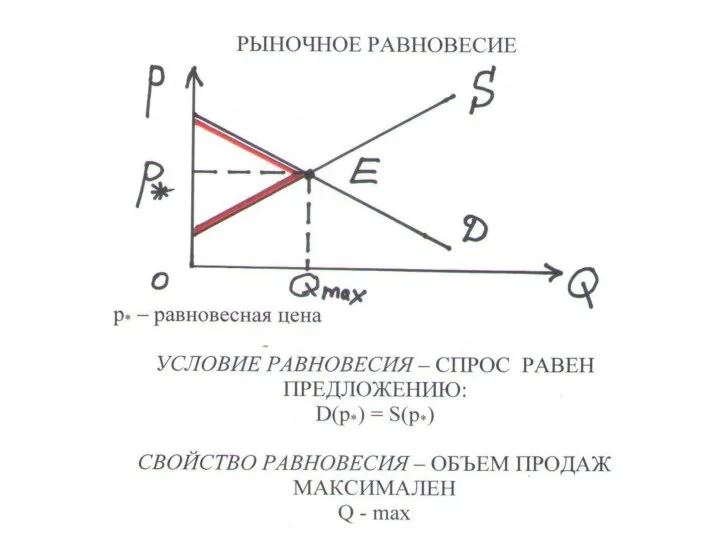
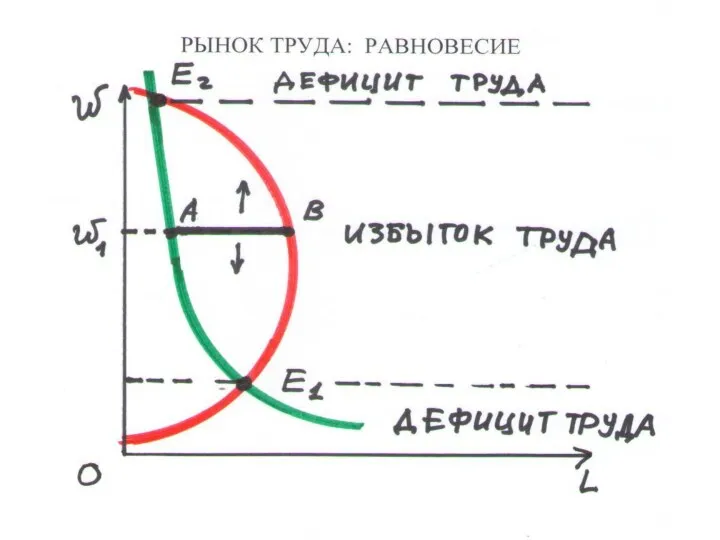
Слайд 31РЫНОЧНОЕ РАВНОВЕСИЕ (2.1)
– объем спроса равен объему предложения:
D(p*) = S(p*), p*

– равновесная цена
ОБЪЕМ ПРОДАЖ – минимум из S и D
РАВНОВЕСНЫЙ ОБЪЕМ ПРОДАЖ Q* – спрос (предложение) при цене p*. Он максимален.
НЕРАВНОВЕСНЫЕ СОСТОЯНИЯ РЫНКА:
ДЕФИЦИТ. Цена меньше равновесной, D > S
В магазинах – очереди. Цена растет
ПЕРЕПРОИЗВОДСТВО. Цена больше p*, D < S
На складах – излишки. Цена снижается
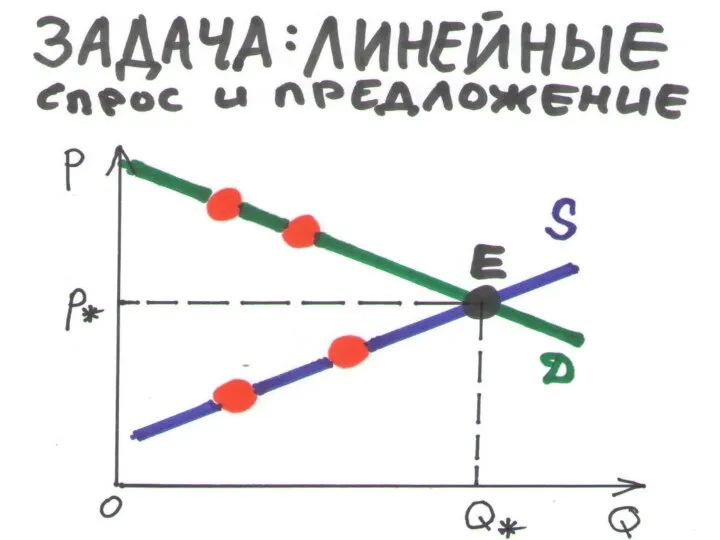
Слайд 33ЗАДАЧА: ЛИНЕЙНЫЕ КРИВЫЕ D и S. ДАНО:
A1(p1,Q1), A2(p2,Q2), A3(p3,Q3), A4(p4,Q4)
• Q

– объем продаж
p1 < p2 < p3 < p4 Q1 < Q2 Q3 > Q4
НАЙТИ линейные D и S, равновесие: p*и Q*
1. Строим по точкам А1 и А2: S = cp – d
2. Строим по точкам А3 и А4: D = a – bp
3. Условие равновесия: cp – d = a – bp
4. Равновесная цена: p* = (a + d)/(b + c)
5. Равновесный объем: Q* = (ac – bd)/(b + c)
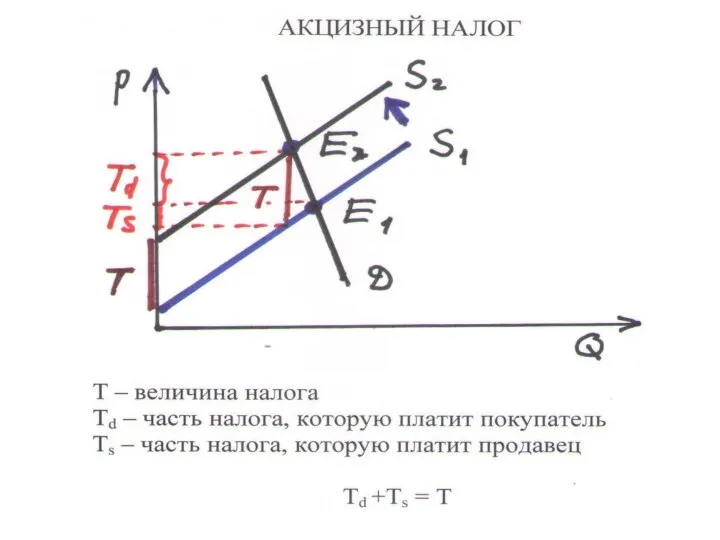
Слайд 35АКЦИЗ (2.3)
– налог, взимаемый с производителя в фиксированном размере с 1

ед. продукции
• Акциз Т увеличивает издержки на величину T
• Кривая S сдвигается вверх на Т единиц
• Равновесная цена растет, объем продаж падает
НАЛОГОВОЕ БРЕМЯ: ПОКУПАТЕЛЯ: Td = p2*– p1*
ПРОИЗВОДИТЕЛЯ: Ts = T – Td
РАСЧЕТ: Td =T·ES/(Ed+Es), TS = T·Ed/(Ed+Es)
где Ed и ES – эластичность спроса и предложения
Следствие: Налоговое бремя больше у субъекта с меньшей эластичностью
Слайд 37ЗАДАЧА ОБ АКЦИЗЕ
ДАНО: D = 22 – p, S = 2p –

5, T = 1
НАЙТИ: Δр, ΔQ, RT (налоговая выручка)
РЕШЕНИЕ
1) 22 – p = 2p – 5 → p1 = 9, Q1 = 13
2) S1 = 2p – 5 → p = 0,5S1 + 2,5 -предложение
3) p = 0,5S2 + 2,5 + 1 → S2 = 2p – 7
4) 22 – p = 2p – 7 → p2 = 9,7, Q2 = 12,3
5) Δp = 9,7 – 9 = 0,7, ΔQ = 12,3 – 13 = - 0,7
6) RT = T· Q2 = 1·12,3 = 12,3
Слайд 38ЗАДАЧА ОБ АКЦИЗЕ (окончание)
НАЙТИ акциз Т, после которого Q↓10%
1) НОВЫЙ ОБЪЕМ ПРОДАЖ:

Q2 = 0,9·Q1 = 0,9·13 = 11,7
2) НОВАЯ КРИВАЯ S: p = 0,5S + 2,5 + T
3) СПРОС НЕИЗМЕНЕН: p = 22 – Q
4) НОВОЕ РАВНОВЕСИЕ:
0,5Q2 + 2,5 + T = 22 – Q2
0,5·11,7 + 2,5 + T = 22 – 11,7 T = 1,95
Слайд 39ЗАДАЧА О СУБСИДИИ
ДАНО: D = 22 – p, S = 2p –

5, S = 1
НАЙТИ: Δр, ΔQ, RS (сумма субсидий)
РЕШЕНИЕ
1) 22 – p = 2p – 5 → p1 = 9, Q1 = 13
2) S1 = 2p – 5 → p = 0,5S1 + 2,5
3) p = 0,5S2 + 2,5 – 1 → S2 = 2p – 3
4) 22 – p = 2p – 3 → p2 = 8,3, Q2 = 13,7
5) Δp = 8,3 – 9 = - 0,7, ΔQ = 13,7 – 13 = 0,7
6) RS = S· Q2 = 1·13,7 = 13,7
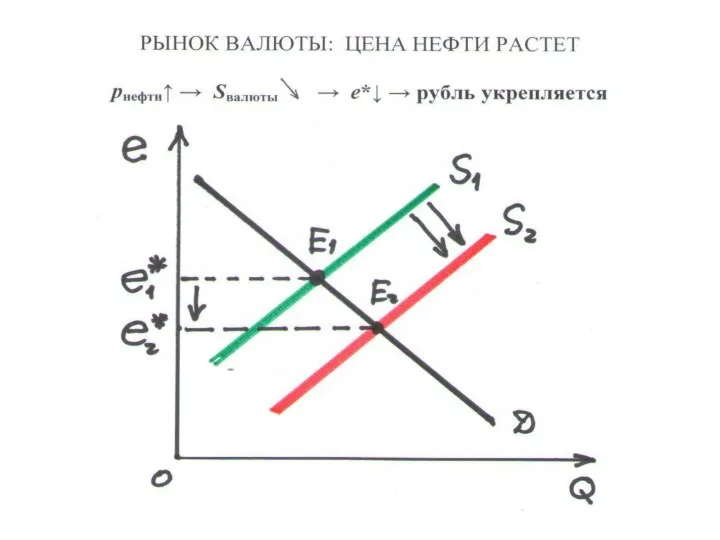
Слайд 40ВАЛЮТНЫЙ РЫНОК (2.2)
ОБМЕННЫЙ КУРС –ЦЕНА $: p = e [руб./долл.]
ОБМЕН ВАЛЮТЫ –
![ВАЛЮТНЫЙ РЫНОК (2.2) ОБМЕННЫЙ КУРС –ЦЕНА $: p = e [руб./долл.] ОБМЕН](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1049811/slide-39.jpg)
ПРОДАЖА И ПОКУПКА $
ПРОДАВЦЫ: • ЦБ, банки, спекулянты, д/хозяйства
• экспортеры • иностранцы в России
ПОКУПАТЕЛИ:• ЦБ, банки,спекулянты д/хозяйства
• импортеры • россияне за рубежом
ПЛАВАЮЩИЙ КУРС –РАВНОВЕСНАЯ ЦЕНА $ (е*)
УКРЕПЛЕНИЕ РУБЛЯ – СНИЖЕНИЕ е*
ОСЛАБЛЕНИЕ РУБЛЯ – УВЕЛИЧЕНИЕ е*
Слайд 42ПОТРЕБЛЕНИЕ (Доп. 1)
ПОЛЕЗНОСТЬ – удовлетворение, которое доставляет индивиду потребление некоторого набора благ

(продуктов)
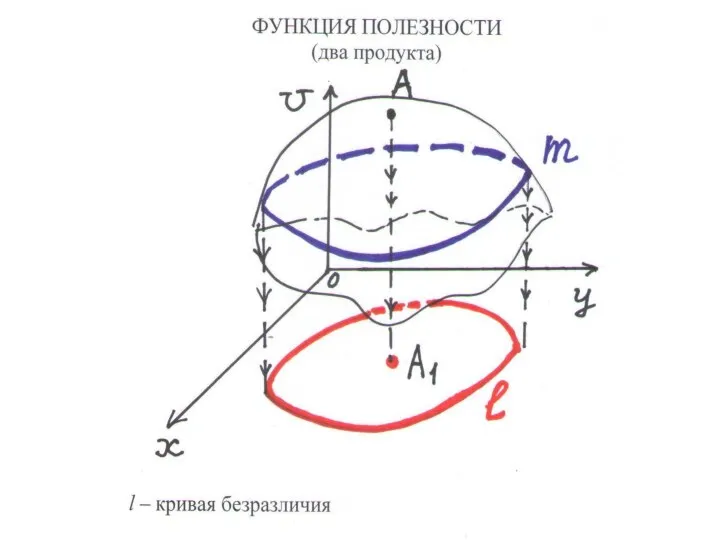
ФУНКЦИЯ ПОЛЕЗНОСТИ – зависимость полезности (U) от объемов потребления продуктов: U = f(x1, …, xn)
где xj – объем потребления j-го продукта, n – количество продуктов
СВОЙСТВА: • U(0,0) = 0
• Полезность субъективна • Антиполезность – когда U < 0
Слайд 43ПОТРЕБЛЕНИЕ ОДНОГО ПРОДУКТА (Доп. 1)
ФУНКЦИЯ ПОЛЕЗНОСТИ: U(x) или Ui.
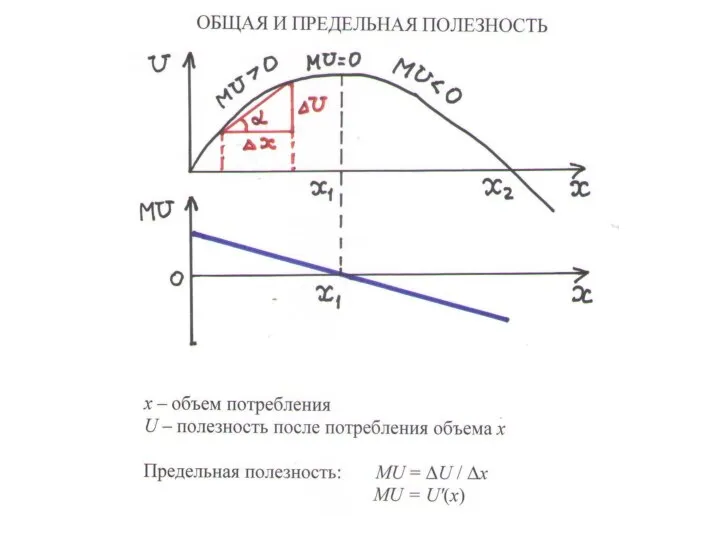
ПРЕДЕЛЬНАЯ ПОЛЕЗНОСТЬ (MU) –

это добавочная полезность, доставленная последней потребленной единицей продукта:
MU = ΔU : Δx
где ∆U – добавочная полезность, ∆x – добавочный объем потребления. В случае непрерывного потребления: MU = U'(x)
Дискретное потребление: MUi = Ui – Ui-1
U РАСТЕТ, если MU > 0, товар – благо
U СНИЖАЕТСЯ, если MU < 0, товар – антиблаго
U МАКСИМАЛЬНА, если MU = 0, благо → антиблаго
ПЕРВЫЙ ЗАКОН ГОССЕНА – с ростом объема потребления предельная полезность уменьшается: x↑ → MU↓
Слайд 45ИЗЛИШЕК ПОТРЕБИТЕЛЯ
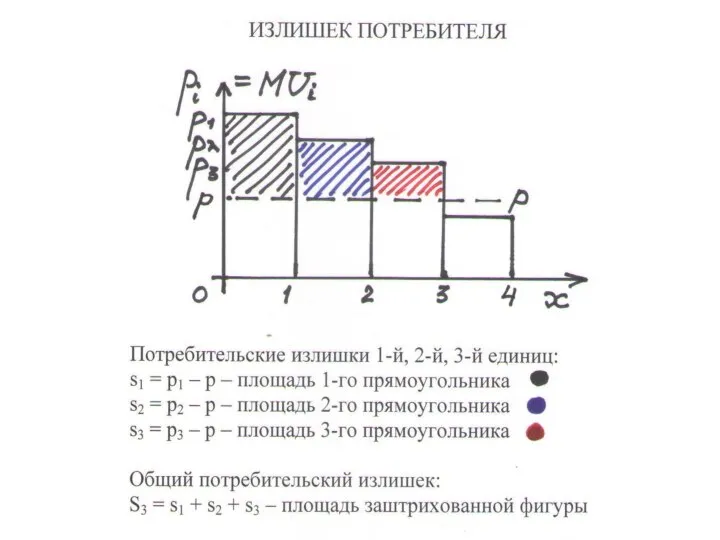
ЦЕНА СПРОСА i-й единицы продукта – максимальная сумма, которую готов за

нее заплатить потребитель
• равна предельной полезности i-й единицы продукта
pi = MUi
ИЗЛИШЕК ПОТРЕБИТЕЛЯ i-ой единицы продукта (si) –
это цена спроса минус рыночная цена (р): si = pi – p
• результат минус затраты, аналог прибыли
СВОЙСТВА: • может быть больше 0, меньше 0 или равен 0
• убывает с ростом объема потребления (Госсен)
СУММАРНЫЙ ИЗЛИШЕК для n единиц: Sn = s1 + … + sn
РЫНОЧНЫЙ ИЗЛИШЕК – сумма излишков всех потребителей (потребители одинаковы)
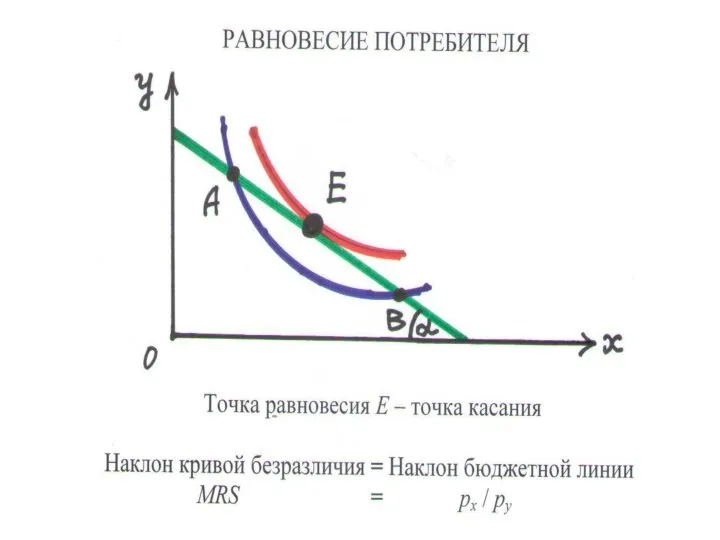
Слайд 47РАВНОВЕСИЕ ПОТРЕБИТЕЛЯ (Доп. 2)
– его суммарный излишек максимален при заданной цене продукта

Sn → max
УСЛОВИЕ РАВНОВЕСИЯ
• потребительский излишек последней единицы равен нулю: sn = 0
• предельная полезность (цена спроса) равна рыночной цене MU = p
• кривая спроса (MU) пересекается с горизонталью р
ВЫВОД: Кривая предельной полезности совпадает с кривой спроса потребителя
Слайд 48ЗАДАЧА ОБ ИЗЛИШКЕ
ДАНО: р1 = 10, р2 = 8, р3 = 6...

Цена: р = 5
НАЙТИ: объем i* (Q*), максимальный излишек S*
1) ЦЕНА СПРОСА: pi = 12 – 2i
2) ИЗЛИШЕК: si = pi – p = 7 – 2i
3) РАВНОВЕСИЕ: si = 7 – 2i = 0 → i = 3,5 → i* = 3
4) РАСЧЕТ МАКСИМАЛЬНОГО ИЗЛИШКА
а) s1 = 7 – 2 = 5, s3 = 7 – 6 = 1
б) S* = 0,5·(s1 + s2)·i* = 0,5(5 + 1)3= 9
5) ЗАТРАТЫ: • Если I > C*, то i = i*, C* = pi* = 5·3 = 15
• Если I < C*, то i = целая часть(I/p)
Слайд 49ПОТРЕБЛЕНИЕ ДВУХ ПРОДУКТОВ (Доп. 1)
ФУНКЦИЯ ПОЛЕЗНОСТИ: U(x,y) или Uij.
ПРЕДЕЛЬНЫЕ ПОЛЕЗНОСТИ:
MUx =

ΔU:Δx, MUy = ΔU:Δy
U РАСТЕТ, если x↑ при MUx > 0 или
y↑ при MUy > 0
U СНИЖАЕТСЯ, если x↑ при MUx < 0 или
y↑ при MUy < 0
U МАКСИМАЛЬНA, если MUx = 0 и MUy = 0
ПЕРВЫЙ ЗАКОН ГОССЕНА:
x↑ → MUx↓, y↑ → MUy↓
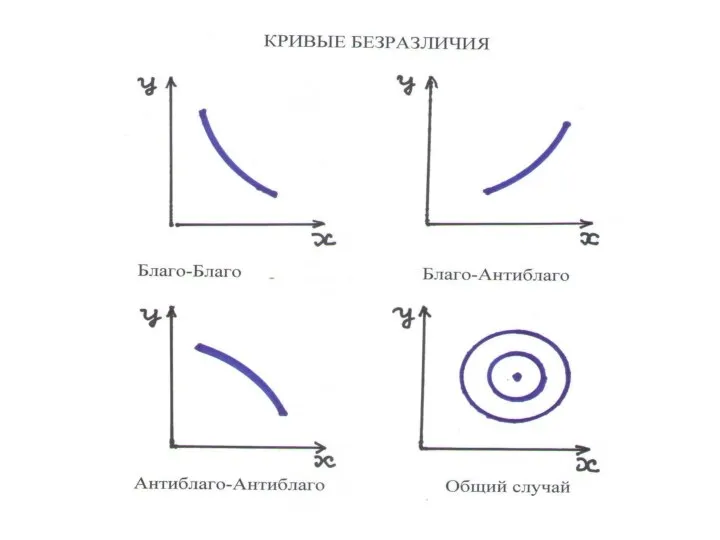
Слайд 51КРИВАЯ БЕЗРАЗЛИЧИЯ:
• наборы продуктов (x,y) с равной полезностью
• проекция точек поверхности U(x,y),

находящихся на равной высоте
• наборы (x,y), удовлетворяющие условию
U(x,y) = const
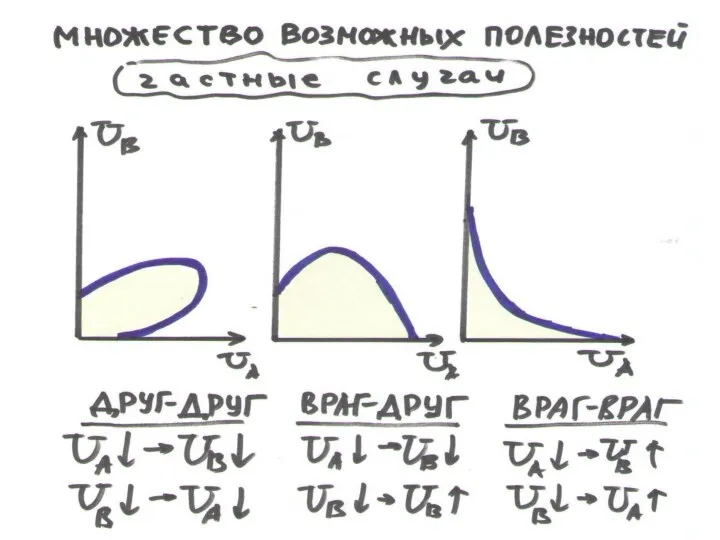
ВИДЫ КРИВЫХ БЕЗРАЗЛИЧИЯ:
БЛАГО – БЛАГО: кривые нисходящие
БЛАГО – АНТИБЛАГО: кривые восходящие
ОБЩИЙ СЛУЧАЙ: кривые замкнуты
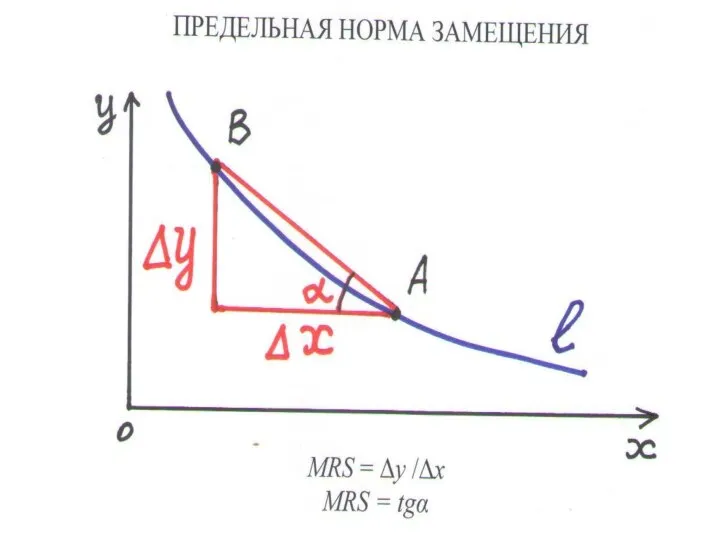
Слайд 53ПРЕДЕЛЬНАЯ НОРМА ЗАМЕЩЕНИЯ
– количество 2-го продукта, от потребления которого вынужден отказаться индивид

при увеличении объема потребления 1-го продукта на 1 ед. при неизменной полезности:
MRS = Δy : Δx
∆x,∆y– изменение объемов потребления (модуль)
MRS – тангенс угла наклона касательной к кривой безразличия
MRS – ценность X, выраженная в единицах Y
MRS снижается с ростом потребления X (Госсен)
MRS – отношение предельных полезностей:
MRS = Δy:Δx= (ΔU/Δx):(ΔU/Δy)=MUx:MUy
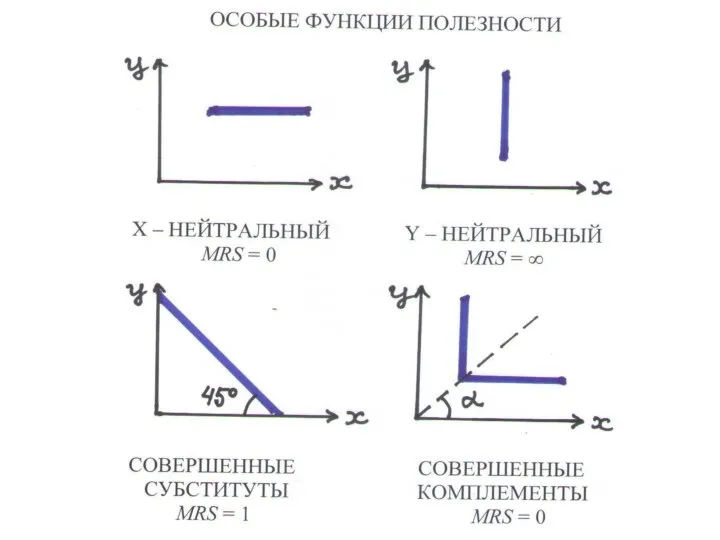
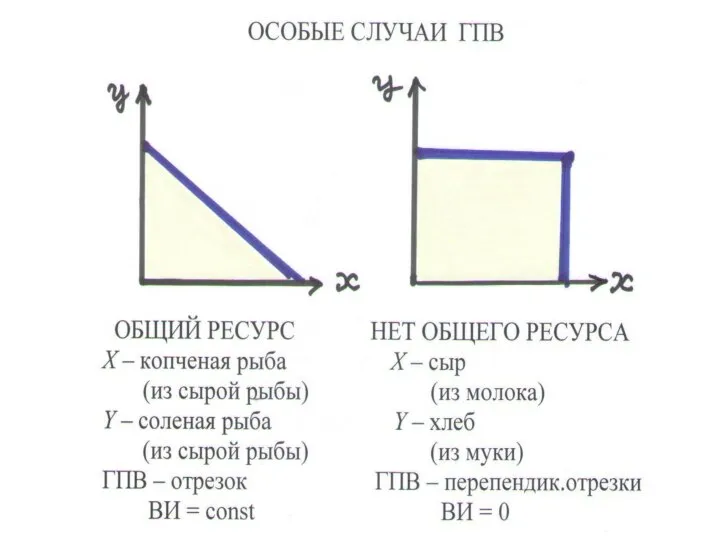
Слайд 55ОСОБЫЕ СЛУЧАИ MRS
СОВЕРШЕННЫЕ СУБСТИТУТЫ – потребителю безразлично, какой из двух продуктов

потреблять:
U(x + y), MRS = 1
Кривая безразличия – отрезок с наклоном 45о
СОВЕРШЕННЫЕ КОМПЛЕМЕНТЫ – потребляются только в комплекте (пара обуви)
U(min(x,y)), MRS = 0
Кривая безразличия – два луча, параллельны осям
Х НЕЙТРАЛЕН –полезность не зависит от объема Х
U(y), MRS = 0
Кривая безразличия горизонтальна
Y НЕЙТРАЛЕН –полезность не зависит от объема Y
U(x), MRS = ∞
Кривая безразличия вертикальна
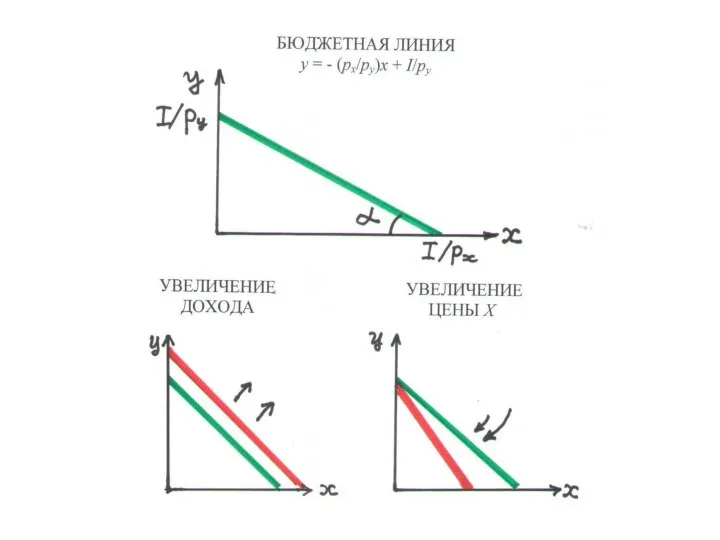
Слайд 57БЮДЖЕТНАЯ ЛИНИЯ (Доп. 1)
точки (x, y), удовлетворяющие бюджетному ограничению: pxx + pyy

= I,
px, py – цены X, Y; I – бюджет потребителя
• форма записи: y = –(px /py )x + I/py
• отрезок с тангенсом угла наклона px/py
• максимальное потребление X равно I/px
• максимальное потребление Y равно I/py
СДВИГИ
• параллельный сдвиг вправо при росте I
• поворот по часовой стрелке при росте px
• поворот против часовой стрелки при росте py
Слайд 59РАВНОВЕСИЕ ПОТРЕБИТЕЛЯ (Доп.2)
–полезность максимальна при доходе I, ценах px, py
U(x,y) →

max, px x + py y = I
УСЛОВИЕ РАВНОВЕСИЯ:
• Удельные предельные полезности равны
MUx : px = MUy : py
• Отношение предельных полезностей равно отношению цен: MUx : MUy = px : py
• Субъективная ценность равна рыночной ценности
MRS = px : py
• Бюджетная линия касается кривой безразличия
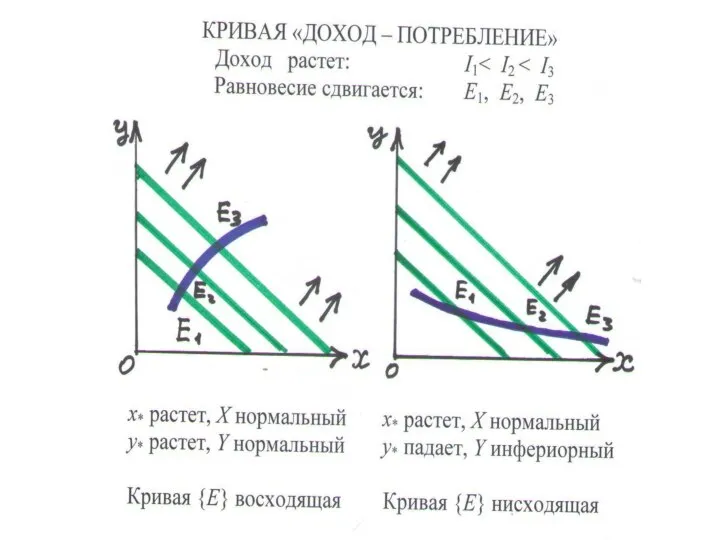
Слайд 61ИЗМЕНЕНИЕ РАВНОВЕСИЯ ПОТРЕБИТЕЛЯ (Доп. 3)
КРИВАЯ «ДОХОД-ПОТРЕБЛЕНИЕ» – равновесные наборы, отвечающие разным доходам

при фиксированных ценах
• ВОСХОДЯЩАЯ – оба товары нормальные
• НИСХОДЯЩАЯ – нормальный и некачествен. товар
• ГОРИЗОНТАЛЬНАЯ – 1-й товар нормальный
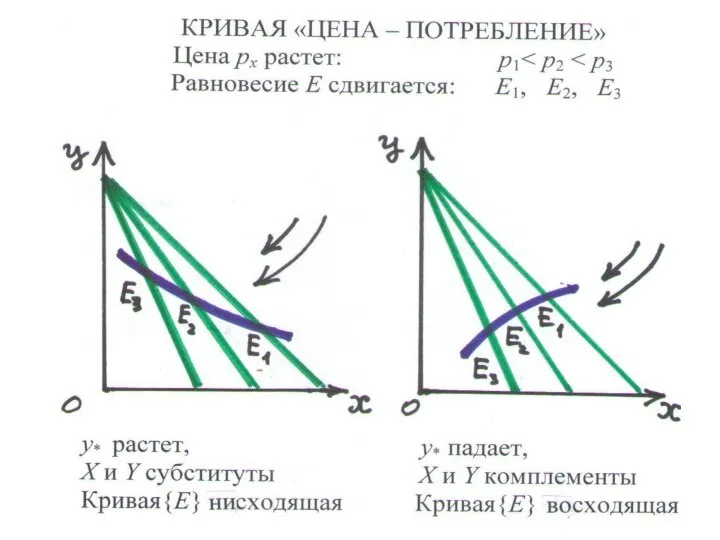
КРИВАЯ «ЦЕНА-ПОТРЕБЛЕНИЕ» – равновесные наборы, отвечающие разным ценам товара при фиксированном доходе и цене другого товара.
• НИСХОДЯЩАЯ – субституты
• ВОСХОДЯЩАЯ – комплементы
• ГОРИЗОНТАЛЬНАЯ – нейтральные
Слайд 64ВТОРОЙ ЗАКОН ГОССЕНА (Доп. 2)
– в равновесии добавочная полезность, доставленная затратой 1

руб. на покупку любого товара, одинакова для всех товаров:
MU1/p1 = … = MUn/pn = λ
• «цена/качество» - одинаково для всех товаров
ПРЕДЕЛЬНАЯ ПОЛЕЗНОСТЬ ДЕНЕГ (λ) – отношение предельной полезности к цене каждого товара при равновесии. Равна приросту общей полезности при увеличении дохода потребителя на 1 руб.:
λ = ΔU/ΔI
• с ростом дохода I величина λ снижается
Слайд 65ЗАДАЧА О РАВНОВЕСИИ ПОТРЕБИТЕЛЯ
ДАНО: p1 =1, p2 =2, I =6, U =

x + 2y0,5
НАЙТИ: х1*, y2*, U* РЕШЕНИЕ:
1) ВЫРАЗИМ: x + 2y = 6 → x = 6 – 2y
2) ПОДСТАВИМ: U = 6 – 2y +2y0,5
3) ДИФФЕР-М: U'(y) = –2 + 2/2y0,5 = 0
4) РЕШИМ: y0,5 = 1/2 → y* = 0,25
5) ПОДСТАВИМ x* =6–2y* =6–2∙0,25 =5,5
6) ВЫЧИСЛИМ: U* =5,5+2∙(0,25)0,5 =6,5
Слайд 67ПРОИЗВОДСТВО (3.1)
ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ – зависимость выпуска продукта от объемов используемых ресурсов:
Р =

Q = f(x1, …, xn),
xj – затраты j-го ресурса (единицы ресурса),
n – количество типов ресурсов
СВОЙСТВА
• P(0,0) = 0 • Р ≥ 0
• Для производителей А и В существует РА + РВ
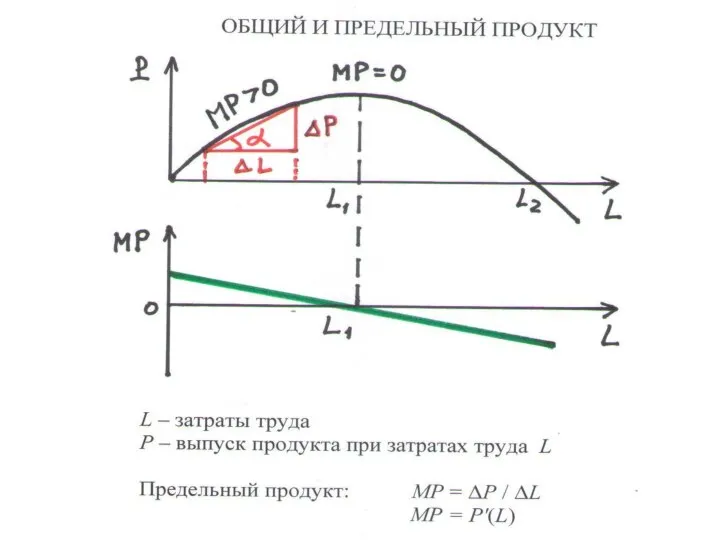
Слайд 68ИСПОЛЬЗОВАНИЕ ОДНОГО ПРОДУКТА (3.1)
ПРОИЗВОДСТВЕН. ФУНКЦИЯ: P(L), L–затраты труда
ПРЕДЕЛЬНЫЙ ПРОДУКТ (ПРЕДЕЛЬНАЯ ПРОИЗВОДИТЕЛЬНОСТЬ) –

прирост выпуска, полученный после использования дополнительной единицы труда:
MP = ΔP : ΔL
∆P – прирост выпуска, ∆L – прирост затрат труда
• MP = P'(L) • MP ≥ 0, т.е. P(L) возрастает
• Выпуск P максимален при MP = 0
Закон УБЫВАЮЩЕЙ ПРОИЗВОДИТЕЛЬНОСТИ: L↑ → MP↓
Слайд 70ПРИБЫЛЬ И РАВНОВЕСИЕ ПРОИЗВОДИТЕЛЯ (4.2)
ЦЕНА СПРОСА НА ТРУД i-го рабочего (wi) –

ставка
зарплаты, которую готов заплатить производитель
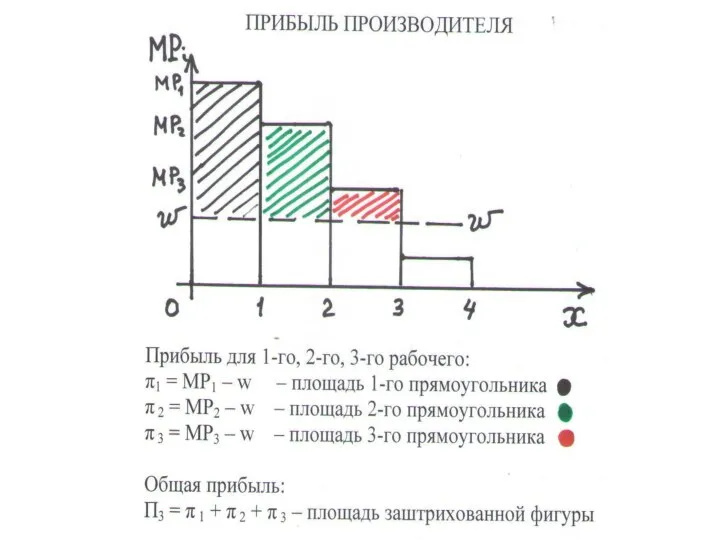
ПРИБЫЛЬ созданная i –м рабочим (πi) – цена спроса минус рыночная цена: πi = wi – w
• πi убывает с ростом L, т.к. МР убывает
ПРИБЫЛЬ при n рабочих: Пn = π1 +…+ πn
РАВНОВЕСИЕ ПОТРЕБИТЕЛЯ: Пn → max
УСЛОВИЕ РАВНОВЕСИЯ (р = 1): MPi = w
УСЛОВИЕ РАВНОВЕСИЯ (р ≠ 1): р·MPi = w
ВЫВОД: Кривая рМР - кривая спроса на труд
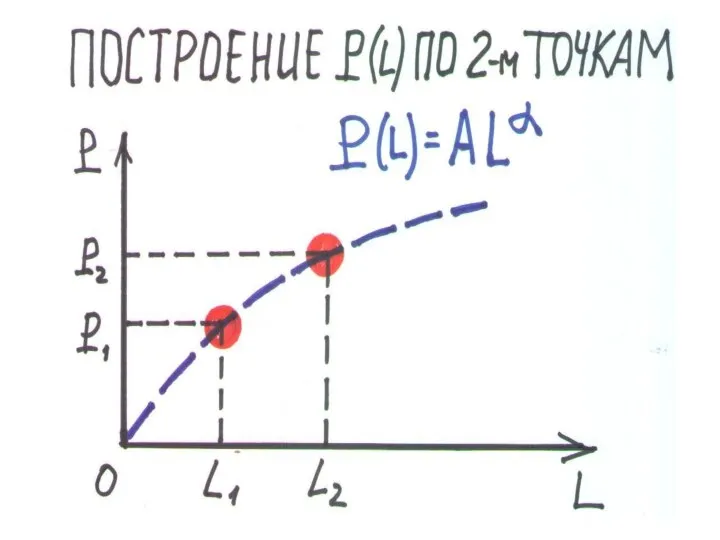
Слайд 71ПОСТРОЕНИЕ P(L) ПО 2-м ТОЧКАМ. ДАНО:
P = ALα, (L1,P1), (L2,P2),

p, w. НАЙТИ L*
1. ЛОГАРИФМИРУЕМ, ПОДСТАВЛЯЕМ ТОЧКИ
lnP1 = lnA + αlnL1
lnP2 = lnA + αlnL2
2. ВЫЧИТАЕМ: ln(P1/P2) = αln(L1/L2)
3. РЕШАЕМ: α = ln(P1/P2):ln(L1/L2), A = P1/L1α
4. РАВНОВЕСИЕ: MPL =w, p(ALα)'=w, pAαLα -1 =w
5. РЕШАЕМ: L* = (pAα/w)1/(1 – α)
Слайд 72ПРИМЕР: ЗАДАЧА О ПОСТРОЕНИИ P(L)
ДАНО: L1 = 2, P1 = 10, L2

= 4, P2 = 12,
p = 2, w = 0,7. НАЙТИ L*
РЕШЕНИЕ: P = ALα
α = ln(10/12) : ln(2/4) = 0,264
A = 10 : 20,264 = 8,326
L*= (2∙8,326∙0,264/0,7)1/0,736 = 12,14
Слайд 74ПОСТРОЕНИЕ P(L) ПО N ТОЧКАМ
ДАНО: (Li, Pi), i = 1,2,…, N, p,

w
НАЙТИ: L* РЕШЕНИЕ: P = ALα
1. ЛОГАРИФМИРУЕМ КООРДИНАТЫ ТОЧЕК
(Li, Pi) → (lnLi, lnPi) → (xi, yi)
2. СТРОИМ УРАВНЕНИЕ РЕГРЕССИИ (Excel)
y = a + bx
3. НАХОДИМ ПАРМЕТРЫ ПРОИЗВ. ФУНКЦИИ
α = b, a = lnA → А = еа
Слайд 76ИСПОЛЬЗОВАНИЕ ДВУХ РЕСУРСОВ (4.2)
ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ: P(L,K)
ПРЕДЕЛЬНЫЕ ПРОДУКТЫ труда и капитала:
MPL = ΔP

: ΔL MPK = ΔP : ΔK
• MPL ≥ 0, MPK ≥ 0 – функции двух переменных
• Выпуск Р максимален, если MPL = MPK = 0
• ЗАКОН УБЫВАЮЩЕЙ ПРОИЗВОДИТЕЛЬНОСТИ:
L↑ → MPL↓ K↑ → MPK↓
ИЗОКВАНТА – изображение наборов (L,K), обеспечивающих равный выпуск. Кривая нисходящая. Чем она дальше от начала координат, тем больше выпуск
Слайд 77ПРЕДЕЛЬНАЯ НОРМА ТЕХНОЛОГИЧЕСКОГО ЗАМЕЩЕНИЯ
– количество капитала, от использования которого следует отказаться при

увеличении затрат труда на 1 при сохранении неизменным выпуска:
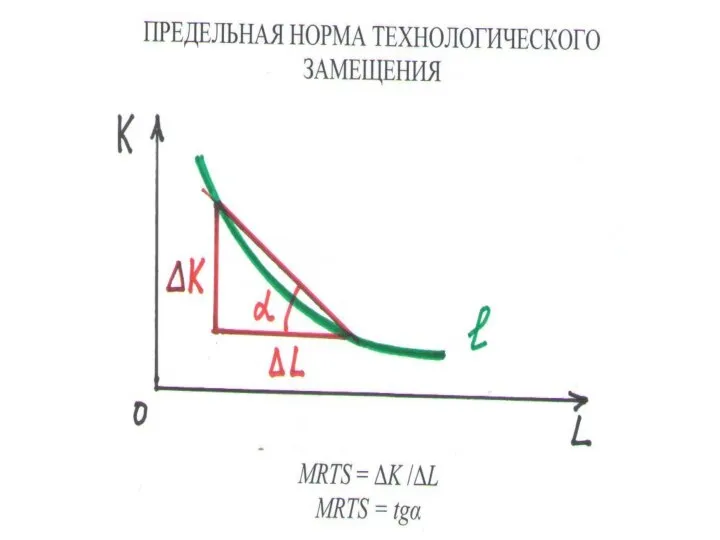
MRTS = ΔK : ΔL
∆L и ∆K – приросты затрат труда и капитала
MRTS – тангенс угла наклона касательной к изокванте
MRTS – ценность труда, выраженная в единицах капитала; определяется технологией
MRTS уменьшается с ростом затрат труда (закон убывающей предельной производительности)
MRTS – отношение предельных продуктов:
MRTS = MPL : MPK
Слайд 79ИЗОКОСТА
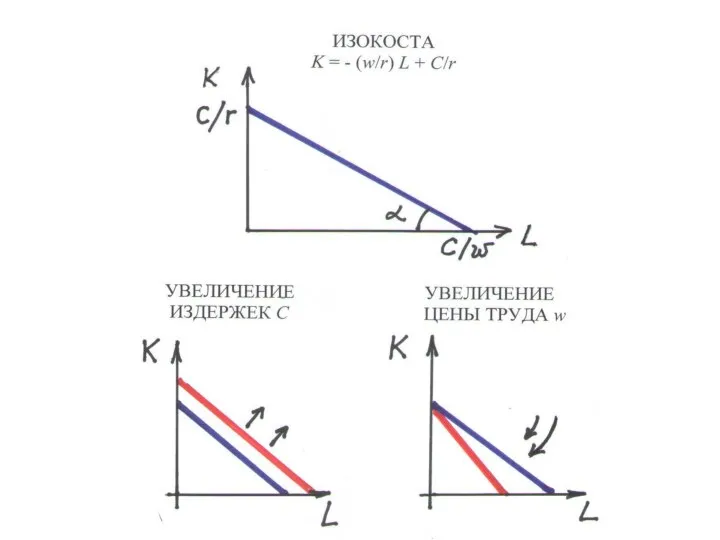
– наборы затрат ресурсов, удовлетворяющие бюджетному ограничению:
wL + rK = C

r – цена капитала, С – издержки производителя
– наборы затрат ресурсов равной стоимости
- аналог бюджетной линии потребителя
• отрезок с тангенсом угла наклона w/r
• максим. затраты: труда = C/w, капитала = C/r
• при росте С изокоста сдвигается вправо
• при росте w поворачивается по часовой стрелке
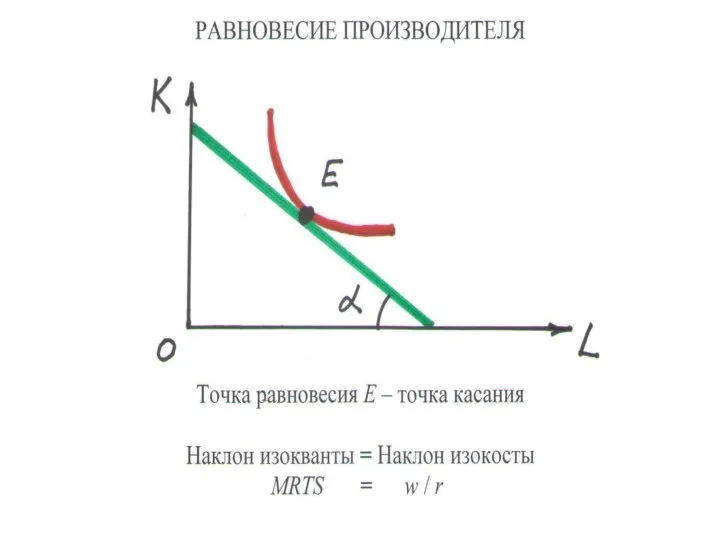
Слайд 81РАВНОВЕСИЕ ПРОИЗВОДИТЕЛЯ (4.2)
– выпуск максимален при издержках С и ценах w,

r
P(L,K) → max, wL + rK = C
УСЛОВИЕ РАВНОВЕСИЯ
• Удельные предельные продукты равны
MPL : w = MPK : r
• Отношение предельных продуктов равно относительной цене
MPL : MPK = w : r
• Внутренняя ценность равна рыночной ценности
MRS = w : r
• Изокоста касается изокванты
Слайд 83ОТДАЧА ОТ МАСШТАБА ПРОИЗВОДСТВА (3.1)
УВЕЛИЧЕНИЕ МАСШТАБА ПРОИЗВОДСТВА – пропорциональное увеличение затрат труда

и капитала (в t раз):
(L,K) → (tL,tK), t ≥ 1
P0 = P(L,K) → P1 = P(tL,tK)
ВИДЫ ОТДАЧИ ОТ МАСШТАБА ПРОИЗВОДСТВА:
ПОСТОЯННАЯ ОТДАЧА: Р1/Р0 = t
Рост затрат ресурсов в t раз увеличивает выпуск в t раз: P1 = tP0
Слайд 84ВОЗРАСТАЮЩАЯ ОТДАЧА: Р1/Р0 > t
Рост затрат ресурсов в t раз увеличивает

выпуск более чем в t раз: P1 > tP0
Это – экономия от масштаба
УБЫВАЮЩАЯ ОТДАЧА: Р1/Р0 < t
Рост затрат ресурсов в t раз увеличивает выпуск менее чем в t раз: P1 < tP0
Это – потери от масштаба
Слайд 85ОДНОРОДНАЯ ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ:
P(tL,tK) = tδP(L,K) или P1 = tδP0
• δ – степень

однородности
Если δ = 1, то P1 = tP0 – постоянная отдача от масштаба
Если δ < 1, то P1 < tP0 – убывающая отдача от масштаба
Если δ > 1, то P1 > tP0 – возрастающая отдача от масштаба
Слайд 86ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ КОББА-ДУГЛАСА
P = ALαKβ
А > 0 – производительность, A = P(1,1)
α

≤ 1 – роль труда, эластичность выпуска по L:
α = (ΔP/P) : (ΔL/L)
β ≤ 1– роль капитала, эластичность выпуска по K:
β = (ΔP/P) : (ΔK/K)
Функция однородна со степенью однородности α+β
P(tL,tK) = A(tL)α (tK)β = tα+β P(L,K)
Если α+β = 1, то постоянная отдача от масштаба
Если α+β>1, то возрастающая отдача от масштаба
Если α+β<1, то убывающая отдача от масштаба
Слайд 87ПОСТРОЕНИЕ ФУНКЦИИ К.-ДУГЛАСА ДАНО: Январь: P1, L1, K1 Февраль: P2, L2, K2

ЛОГАРИФМИРУЕМ P = ALαK1-α, ПОДСТАВЛЯЕМ:
ln P1 = ln A + α ln L1 + (1 – α) ln K1
ln P2 = ln A + α ln L2 + (1 – α) ln K2
ВЫЧИТАЕМ, ПОЛУЧАЕМ УРАВНЕНИЕ, НАХОДИМ α:
ln(P1/P2) = αln(L1/L2) + (1 – α)ln(K1/K2)
α = ln(P1K2/P2K1) : ln(L1K2/L2K1)
НАХОДИМ А: α = P1/L1αK11 -α
Слайд 88РАВНОВЕСИЕ. ФУНКЦИЯ К.-ДУГЛАСА
P = ALαK1 – α ДАНО: р = 1, A

= 30,
α = 0,2, w = 5, r = 10, C = 100
ИЗВЕСТНО: L* = Cα/w,
K* = C(1 – α)/r
L* =100·0,2:5 =4, K* =100·0,8:10 =8
Pmax = 30·40,2·80,8 = 208,9
Пmax = 208,9 – 100 = 108,9
Слайд 89КРИВАЯ ПРОИЗВОД. ВОЗМОЖНСТЕЙ (КПВ) (1.3)
Производят продукты X и Y, используя L и

K
x = P1(L1,K1), y = P2(L2,K2); L1 + L2 = L, K1 + K2 = K
ПРОИЗВОДСТВЕННАЯ ВОЗМОЖНОСТЬ – выпуски (x,y), которые можно произвести одновременно при технологиях P1 и Р2 и затратах ресурсов L и K
ГРАНИЦА ПРОИЗВОДСТВЕННЫХ ВОЗМОЖНОСТЕЙ (ГПВ) – множество Парето-оптимальных (эффективных) производственных возможностей
ГПВ сдвигается вправо-вверх:
• при увеличении затрат ресурсов (рост населения)
• при научно-техническом прогрессе (НТП)
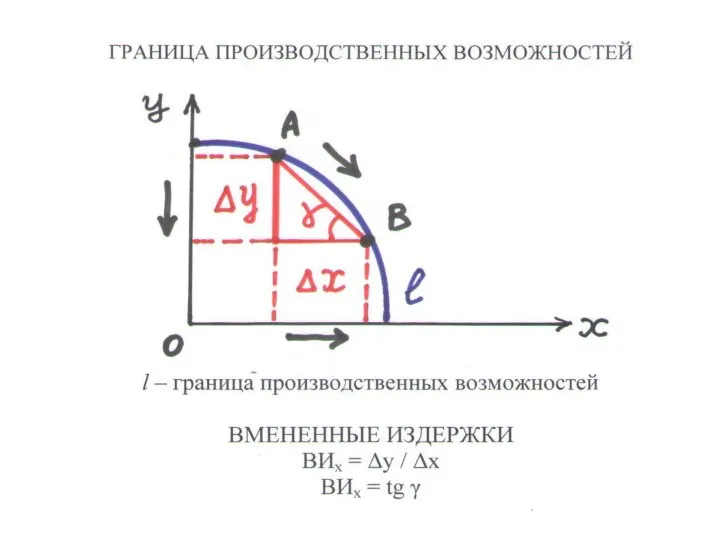
Слайд 90АЛЬТЕРНАТИВНЫЕ (ВМЕНЕННЫЕ) ИЗДЕРЖКИ ПРОДУКТА Х (1.2)
– вынужденное снижение выпуска Y при росте

выпуска Х на 1 ед. на границе производственных возможностей:
ВИх = ∆Y/∆Х
• = тангенсу угла наклона касательной к ГПВ
• ВИх растут с ростом выпуска Х
• ВИх измеряются в [ед. Y/ед. Х ]
• ВИх · ВИy = 1
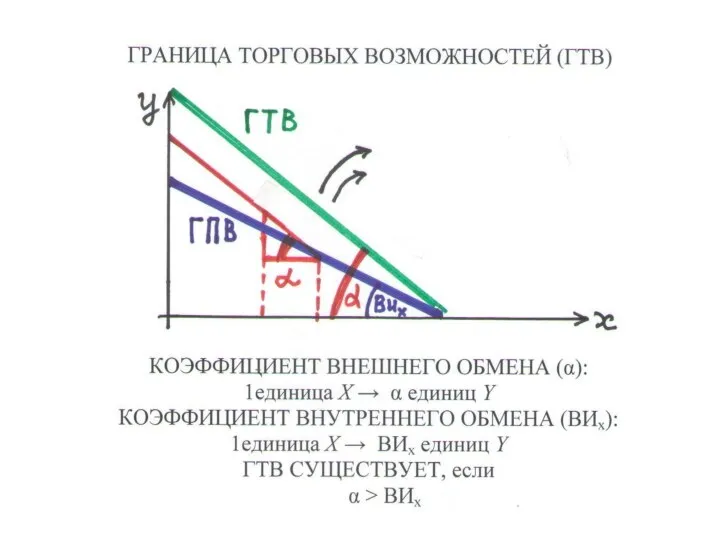
Слайд 93ТОРГОВЫЕ ВОЗМОЖНОСТИ (1.3)
КОЭФФИЦИЕНТ ВНУТРЕННЕГО ОБМЕНА Х – вмененные издержки Х: 1 ед.

Х «обменивают» на ВИХ ед. Y
КОЭФФИЦИЕНТ ВНЕШНЕГО ОБМЕНА Х – другая страна предлагает α ед. Y за 1 ед. Х
ВНЕШНИЙ ОБМЕН ВЫГОДЕН, если α ≥ ВИх
ТОРГОВАЯ ВОЗМОЖНОСТЬ – выпуски (x,y), которые можно получить путем производства или внешнего обмена
ГРАНИЦА ТОРГОВЫХ ВОЗМОЖНОСТЕЙ – множество Перето-оптимальных торговых возможностей
• Множество торговых возможностей шире множества производств. возможностей
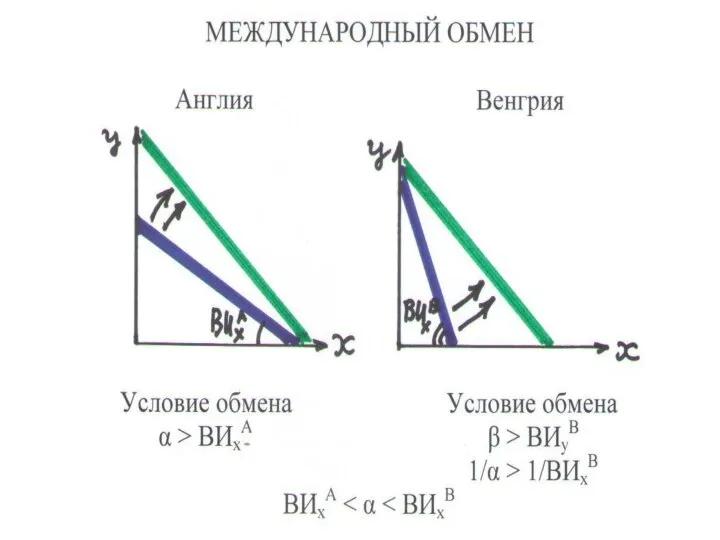
Слайд 95ОБМЕН МЕЖДУ ДВУМЯ СТРАНАМИ
СТРАНА А. Экспорт Х выгоден, если
α ≥ ВИхA
СТРАНА

В. Экспорт Y выгоден, если
β ≥ ВИyB 1/α ≥ 1/BИxB α ≤ ВИхВ
ОБМЕН ВЗАИМОВЫГОДЕН, если:
ВИхA ≤ α ≤ ВИхВ
СРАВНИТЕЛЬНОЕ ПРЕИМУЩЕСТВО во внешней торговле товаром Х – его вмененные издержки меньше, чем в другой стране
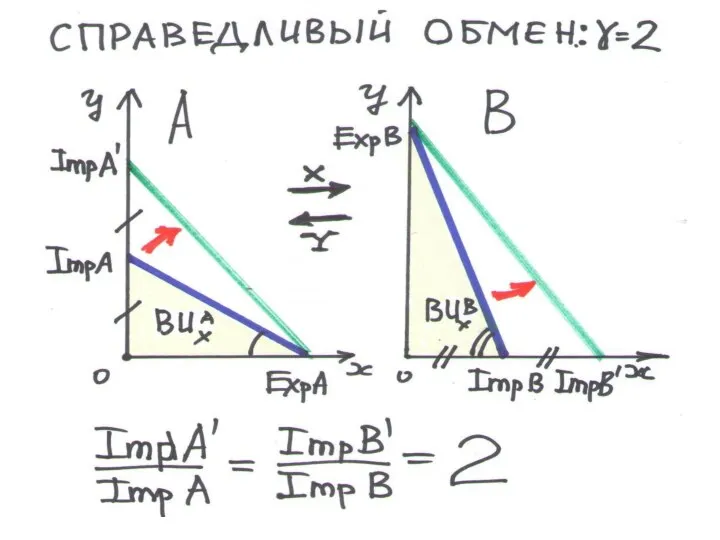
Слайд 97СПРАВЕДЛИВЫЙ ОБМЕН
А экспортирует Х В экспортирует Y
ImpA – макс.выпуск импортируемого продукта

Y
ImpA' – макс. потребление А имп-го продукта после обмена
ImpВ – макс.выпуск импортируемого продукта Х
ImpВ' – макс. потребление в В имп-го продукта после обмена
УСЛОВИЕ СПРАВЕДЛИВОГО ОБМЕНА:
ImpA' : ImpA = ImpВ' : ImpВ = γ
КОЭФФИЦЕНТ СПРАВЕДЛИВОГО ОБМЕНА (γ) – во столько раз вырастет максимальное потребление ввозимого товара в каждой стране поле справедливого обмена
Слайд 99СПРАВЕДЛИВЫЙ ОБМЕН: РАСЧЕТ γ
1) УСЛОВИЕ СПРАВЕДЛИВОГО ОБМЕНА:
ImpA' = γ·ImpA, ImpВ' = γ·ImpВ
2)

УСЛОВИЕ ОБМЕНА (см. рисунок выше):
ImpA' = α·ExpA, ImpВ' = (1/α)·ExpВ
Из 1) и 2) следует:
α = (ВИХВ·ВИХА)0,5
γ = (ВИХВ:ВИХА)0,5
Т.к. А имеет сравнительное преимущество по Х, поэтому ВИХВ ≥ ВИХА, отсюда γ ≥ 1
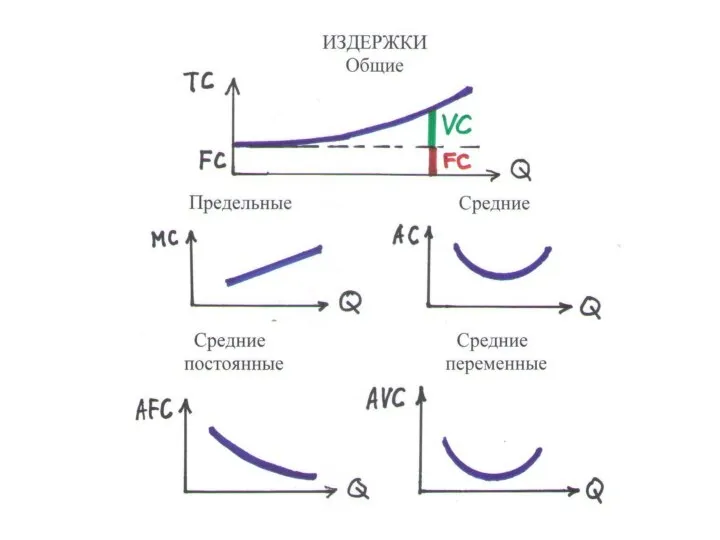
Слайд 101ИЗДЕРЖКИ (3.3) ОБЩИЕ ИЗДЕРЖКИ -
– стоимость ресурсов, затраченных при производстве Q ед.

продукта (TC)
ПРЕДЕЛЬНЫЕ ИЗДЕРЖКИ (МС) (4.1)
– прирост ТС при увеличении выпуска на единицу:
MC = ΔTC/ΔQ = TC'
• возрастают с ростом выпуска
ПОСТОЯННЫЕ ИЗДЕРЖКИ (FC) – не зависят от выпуска (зарплата бухгалтера)
ПЕРЕМЕННЫЕ ИЗДЕРЖКИ (VC) – зависят от выпуска (зарплата рабочих )
TC = FC + VC
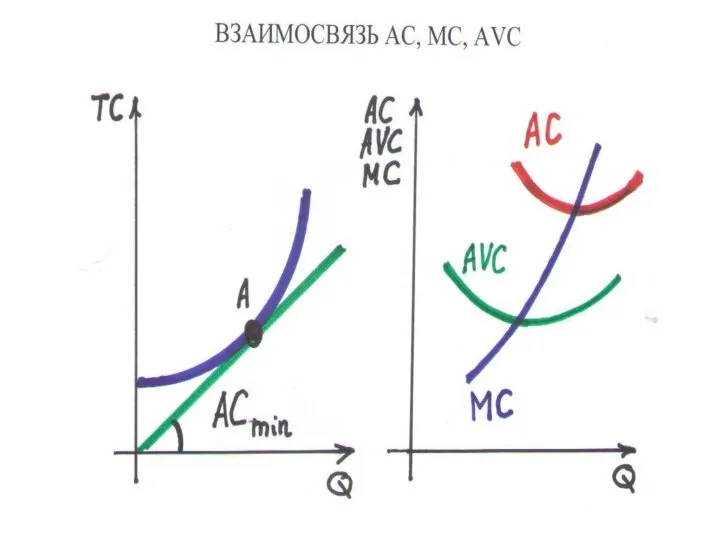
Слайд 102СРЕДНИЕ ИЗДЕРЖКИ
– отношение общих издержек к выпуску (себестоимость единицы продукции)
AC = TC/Q
•

AC минимальны, если МС = АС
СРЕДНИЕ ПОСТОЯННЫЕ ИЗДЕРЖКИ (AFC) – отношение FС к выпуску: AFC = FC/Q
• AFC падают с ростом Q, график – гипербола
СРЕДНИЕ ПЕРЕМЕННЫЕ ИЗДЕРЖКИ (AVC) – отношение VC к выпуску: AVC = VC/Q
• AVC имеют минимум
AC = AFC + AVC
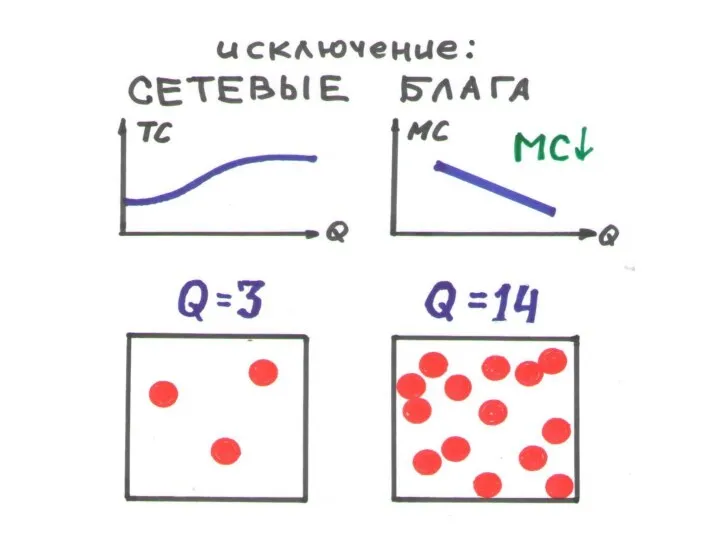
Слайд 106РЫНОЧНЫЕ СТРУКТУРЫ (4.3)
ФИРМА – субъект, который производит и продает продукт, приобретая и

используя ресурсы
КОНКУРЕНТНЫЙ ПРОДАВЕЦ – фирма не способна влиять на рыночную цену продукта
ОЛИГОПОЛИЯ – способна влиять на рыночную цену продукта наряду с другими продавцами
МОНОПОЛИЯ – единственный продавец продукта, устанавливает на него любую цену
КОНКУРЕНТНЫЙ ПОКУПАТЕЛЬ – фирма не способна влиять на рыночную цену ресурса
ОЛИГОПСОНИЯ – способна влиять на рыночную цену ресурса наряду с другими покупателями
МОНОПСОНИЯ – единственный покупатель ресурса, устанавливает на него любую цену
Слайд 107РЫНОЧНАЯ ВЛАСТЬ
– способность фирмы влиять на цену продукта или цену ресурса посредством

изменения выпуска
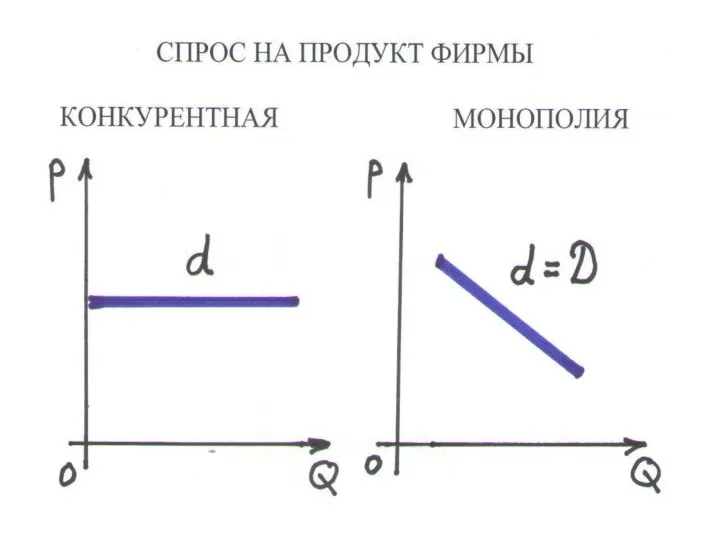
СПРОС НА ПРОДУКТ ФИРМЫ – ее максимальный объем продаж при данной цене
• кривая спроса на продукт фирмы обычно не совпадает с кривой рыночного спроса
РЫНОЧНАЯ ВЛАСТЬ – величина, обратная эластичности спроса на продукт фирмы (1/Е)
КОНКУРЕНТНАЯ ФИРМА. Кривая спроса на продукт фирмы горизонтальна: Е = ∞, 1/Е = 0
МОНОПОЛИЯ. Кривая спроса на продукт фирмы есть кривая рыночного спроса: E = Ed, 1/Еd > 0
Слайд 109ВЫРУЧКА ФИРМЫ
– стоимость проданного товара: TR = p(Q)·Q
СРЕДНЯЯ ВЫРУЧКА – отношение

выручки к объему продаж
AR = TR/Q = pQ / Q = p
ПРЕДЕЛЬНАЯ ВЫРУЧКА – прирост выручки при увеличении объема продаж на единицу:
MR = ΔTR/ΔQ = TR‘
РЫНОЧНАЯ ВЛАСТЬ И MR: MR =TR'=p(1-1/E)
СЛЕДСТВИЯ: • MR ≤ p
• если E > 1, то MR > 0, с ростом Q растет TR
• если E < 1, то MR < 0, с ростом Q падает TR
• если E = 1, то MR = 0, TR максимальна
• если E = ∞, то MR = p, TR прямо пропорциональна Q (конкурентная фирма)
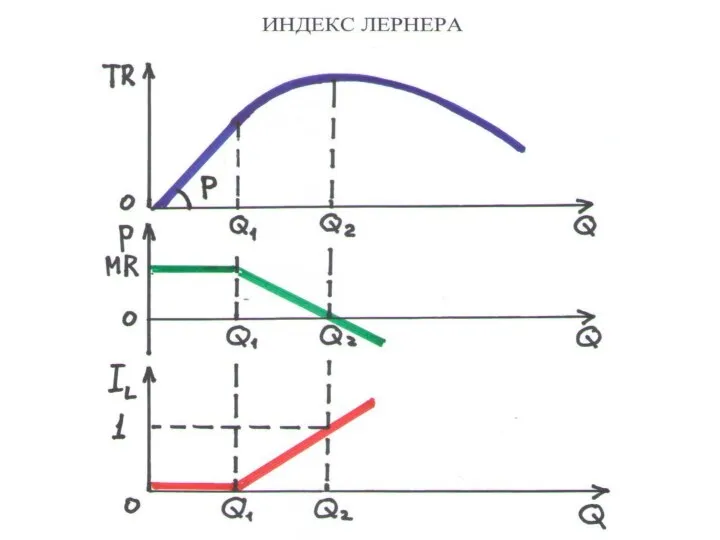
Слайд 110ИНДЕКС ЛЕРНЕРА (4.3)
– степень рыночной власти фирмы (Е – эластичность спроса на

продукт фирмы)
IL = 1/E
MR = p(1 – 1/E) → IL = (p – MR)/p
СВОЙСТВА
IL = 0, фирма конкурентная, MR = р
0 < IL < 1, если 0 < MR < р
IL = 1, ТR максимальна, MR = 0
IL > 1, MR < 0
Слайд 112ИЗМЕРЕНИЕ НЕСОВЕРШЕНСТВА РЫНКА (4.3)
ИНДЕКС ГЕРФИНДАЛЯ (H) – сумма квадратов рыночных долей всех

продавцов на рынке:
H = (α1)2 +…+ (αn)2
n – число продавцов, αi – доля продаж i-го продавца
• при монополии Н = 1
• если на рынке n одинаковых фирм, то Н = 1/n
• при совершенной конкуренции Н ≈ 0, но Н ≠ 0
• при слиянии фирм Н растет, при разделении снижается
ДОЛЯ m КРУПНЕШИХ ФИРМ НА РЫНКЕ (Km)
• при монополии все Km = 1
• если на рынке m фирм, то Km = 1
• при слиянии Km растет, если объем продаж новой фирмы больше объема продаж одной из m крупнейших фирм
Слайд 113РАСЧЕТ Н. На рынке 5 фирм с выпуском 15 и 8 фирм

с выпуском 12
ОБЪЕМ РЫНКА: 5·15 + 8·12 = 171
ДОЛЯ БОЛЬШОЙ: 15:171 = 0,0877
ДОЛЯ МАЛЕНЬКОЙ: 12 :171 = 0,0702
Н = 5·0,08772 + 8·0,07022 = 0,0778
(ПРИБЛИЖЕННО: Н ≈ 1:(5+8) = 1:13 = 0,0769)
НАЙДЕМ Н ПОСЛЕ СЛИЯНИЯ 3-х БОЛЬШИХ ФИРМ
ДОЛЯ НОВОЙ ФИРМЫ: 15·3:171 = 0,2631
Н = 1·0,26312 + 2·0,08772 + 8·0,07022 = 0,1241
Слайд 114ОПРЕДЕЛИМ, на сколько равных частей (n) следует разделить большую фирму, чтобы добиться

Н = 0,073
ДАНО: БОЛЬШИХ фирм – 4 с выпуском 15
МАЛЕНЬКИХ фирм – 8 с выпуском 12
Решение: НОВЫХ фирм – n с выпуском 15/n
ДОЛЯ НОВОЙ ФИРМЫ:
15/n : 171 = 1/11,4n
Н=3·0,0882+8·0,0702+n·(1/11,4n)2= 0,073
РЕШАЕМ УРАВНЕНИЕ: n = 2,75. ОТВЕТ: n =3
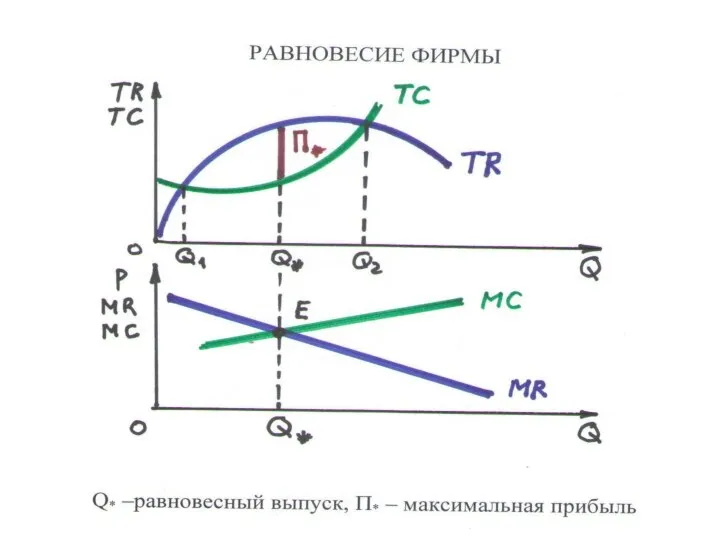
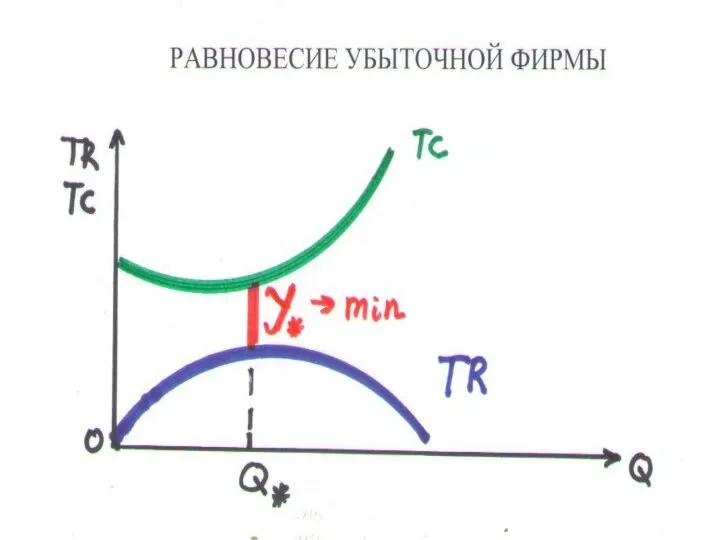
Слайд 115РАВНОВЕСИЕ ФИРМЫ (4.2)
ПРИБЫЛЬ – разность выручки и издержек
П(Q) = TR(Q) – TC(Q)
УБЫТОК

(У) – модуль отрицательной прибыли
РАВНОВЕСИЕ ФИРМЫ – прибыль максимальна
П → max, П' = 0, TR' – TC' = 0
УСЛОВИЕ РАВНОВЕСИЯ: MR = MC
• прирост Q влечет равный прирост TR и ТС
• касательные к кривым TR и ТС параллельны
• изменение выпуска снижает прибыль
Слайд 118ЗАДАЧА О РАВНОВЕСИИ ФИРМЫ. ДАНО: Спрос на продукт фирмы и издержки:
p =

30 – 2Q, TC = 12 + Q2
НАЙТИ РАВНОВЕСНЫЙ ВЫПУСК Q*
1) MC = TC'= (12 + Q2)' = 2Q
2) TR = pQ = (30 – 2Q)Q = 30Q – 2Q2
3) MR = TR' = 30 – 4Q
4) MR = MC, 30 – 4Q = 2Q, Q* = 5
Слайд 119СОВЕРШЕННАЯ КОНКУРЕНЦИЯ (4.4)
– каждая фирма может продать по рыноч. цене любой объем

продукции, она не влияет на цену
УСЛОВИЯ СОВЕРШЕННОЙ КОНКУРЕНЦИИ
1. ОДНОРОДНОСТЬ ПРОДУКТА – все его единицы одинаковы в представлении покупателей
2. МАЛОСТЬ ФИРМ – их объемы спроса и предложения занимают ничтожную долю рынка
3. СВОБОДА ВХОДА И ВЫХОДА – фирмы свободно выходят на рынок и уходят с него , т.е. нет барьеров
4. СОВЕРШЕННАЯ МОБИЛЬНОСТЬ – нет прикрепления покупателей к продавцам, и наоборот
5. СОВЕРШЕННАЯ ИНФОРМИРОВАННОСТЬ – информация распространяется мгновенно, бесплатно и симметрично
6. НУЛЕВЫЕ ТРАНСАКЦИОННЫЕ ИЗДЕРЖКИ – фирмы не несут издержек на осуществление сделок
7. ЕДИНАЯ ЦЕНА
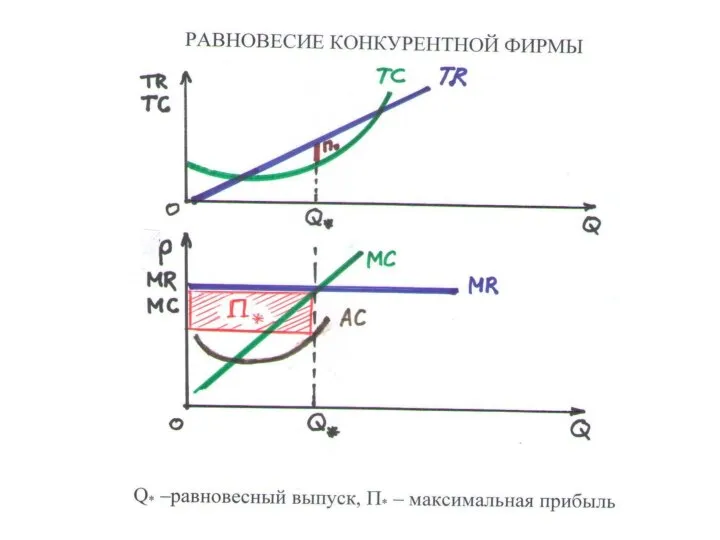
Слайд 120РАВНОВЕСИЕ КОНКУРЕНТНОЙ ФИРМЫ (4.4)
УСЛОВИЕ РАВНОВЕСИЯ:
MR = MC, MR = p MC

= p
РАВНОВЕСНАЯ (МАКСИМАЛЬНАЯ) ПРИБЫЛЬ
П* = (p – AC*)·Q*
p – постоянная рыночная цена, Q* – равновесный выпуск, AC* – средние издержки при равновесном выпуске
НЕРАВНОВЕСНЫЕ СОСТОЯНИЯ
• p > MC, то следует увеличивать выпуск
• p < MC , то следует сокращать выпуск
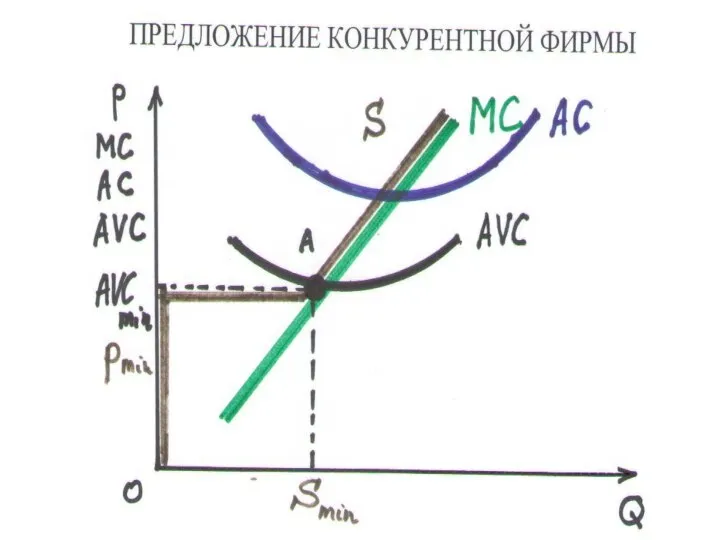
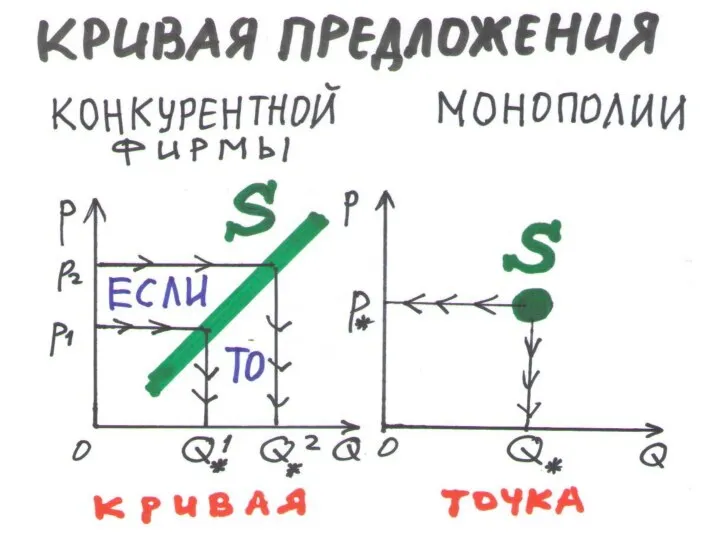
Слайд 122ПРЕДЛОЖЕНИЕ КОНКУРЕНТНОЙ ФИРМЫ
ОБЪЕМ ПРЕДЛОЖЕНИЯ – есть равновесный выпуск
КРИВАЯ ПРЕДЛОЖЕНИЯ – часть кривой

МС
p = MC(S), p ≥ pmin
ЗАПИШЕМ УБЫТКИ, если ПРОИЗВОДСТВО:
ПРОДОЛЖАЕТСЯ: У1 = TC – pQ ≥ 0
ПРЕКРАЩАЕТСЯ: У2 = FC
УСЛОВИЕ ПРОДОЛЖЕНИЯ ПРОИЗВОДСТВА: У1 ≤ У2
TC – pQ ≤ FC, TC – FC ≤ Pq, VC ≤ pQ, p ≥ AVC ,
pmin = AVCmin - миним. цена предложения
ВЫВОД: Фирме следует прекращать производство, когда цена ниже миним. средних переменных издержек
Слайд 125ЗАДАЧА О КРИВОЙ ПРЕДЛОЖЕНИЯ. ДАНО:
TC = 10 + 6Q – 2Q2

+Q3/3. НАЙТИ S
РЕШЕНИЕ: 1. ДИФФЕРЕНЦИРУЕМ ТС:
MC = 6 – 4Q +Q2 = 2 + (Q – 2)2
2. РАВНОВЕСИЕ: МС = р, 2 + (Q – 2)2 = p
3. ВЫРАЗИМ Q через p: S = 2 + (p – 2)0,5
4. ПЕРЕМЕННЫЕ ИЗДЕРЖКИ: VC = 6Q– 2Q2 +Q3/3
5. СРЕДНИЕ VC: AVC = VC:Q = 6 – 2Q + Q2/3
6. НАЙДЕМ AVCmin: AVC' = 0, –2 + 2Q/3 = 0, Q = 3
7. AVCmin = AVC(3) = 6 – 2×3 + 32/3 = 3 = pmin
ОТВЕТ: при р ≥ 3 S = 2 + (p – 2)0,5
Слайд 126Равновесие монополии - торговца
(цена закупки АС = 9)
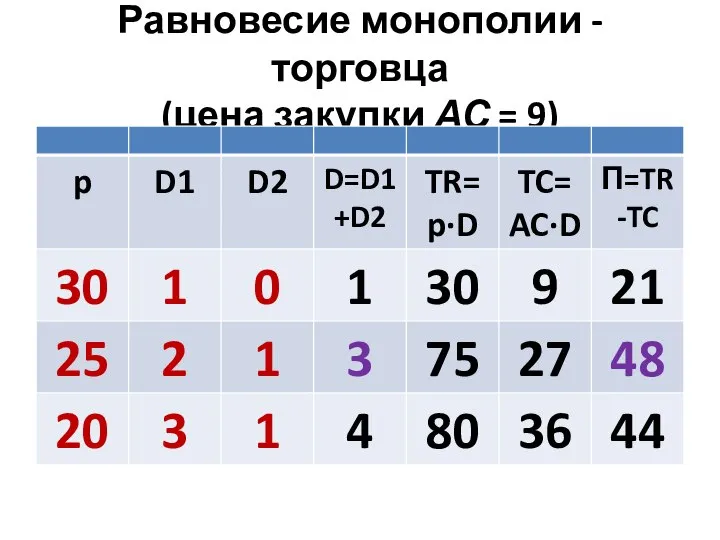
Слайд 128МОНОПОЛИЯ (4.5)
МОНОПОЛИЗАЦИЯ РЫНКА – объединение конкурентных фирм в одну фирму
КРИВАЯ МС

МОНОПОЛИИ совпадает:
• с суммой кривых предельных издержек всех фирм
• с кривой предложения на совершенном рынке
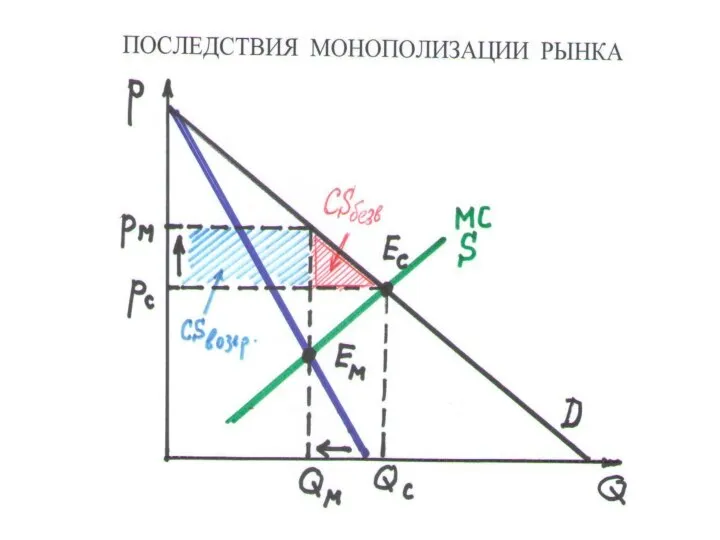
ПОСЛЕДСТВИЯ монополизации рынка:
• снижение рыночного выпуска
• рост равновесной цены
• снижение излишка потребителей
Слайд 129УЩЕРБ, ПРИНОСИМЫЙ МОНОПОЛИЕЙ – сокращение излишка потребителей вследствие монополизации рынка
СОСТОИТ ИЗ ДВУХ

ЧАСТЕЙ:
• ВОЗВРАТНЫЕ ПОТЕРИ (CSвозвр) – часть излишка, которая превращается в прибыль монополии (прямоугольник)
• БЕЗВОЗВРАТНЫЕ ПОТЕРИ (CSбезв) – часть излишка, которая потеряна для общества (треугольник)
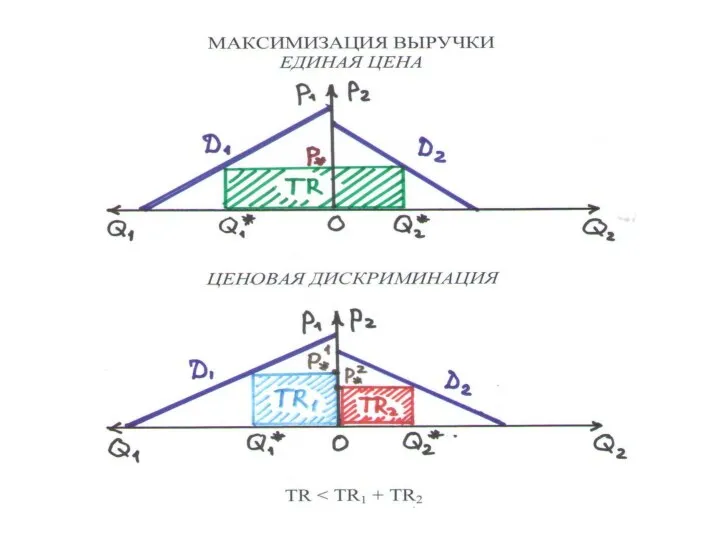
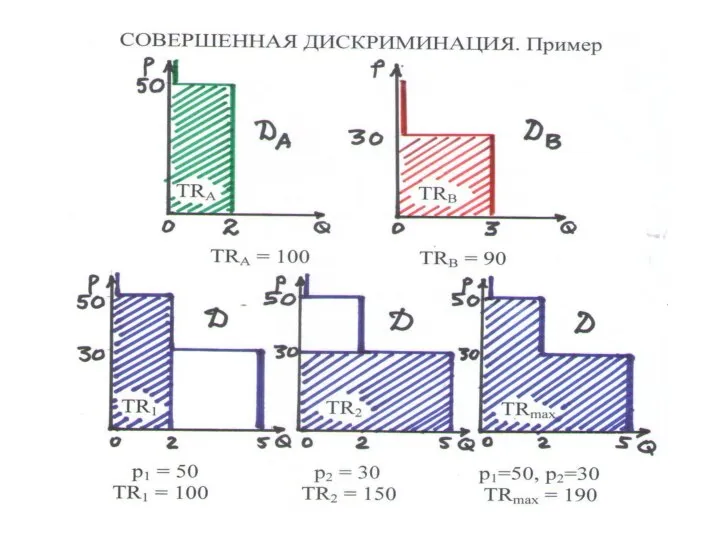
Слайд 131ЦЕНОВАЯ ДИСКРИМИНАЦИЯ (4.5)
– монополия устанавливает разные цены разным покупателям на один и

тот же товар с целью максимизации прибыли
УСЛОВИЕ – нельзя перепродать товар (услуги)
РАЗРЕШЕНА – если она способствует решению социальных проблем (детские билеты)
СЕГМЕНТ РЫНКА – покупатели с одинаковыми кривыми спроса. СЕГМЕНТИРОВАННЫЙ РЫНОК – покупатели разбиты на сегменты
ВЫРУЧКА: TR = TR1(Q1) + TR2(Q2)
Q1, Q2 – объемы продаж в сегментах 1 и 2
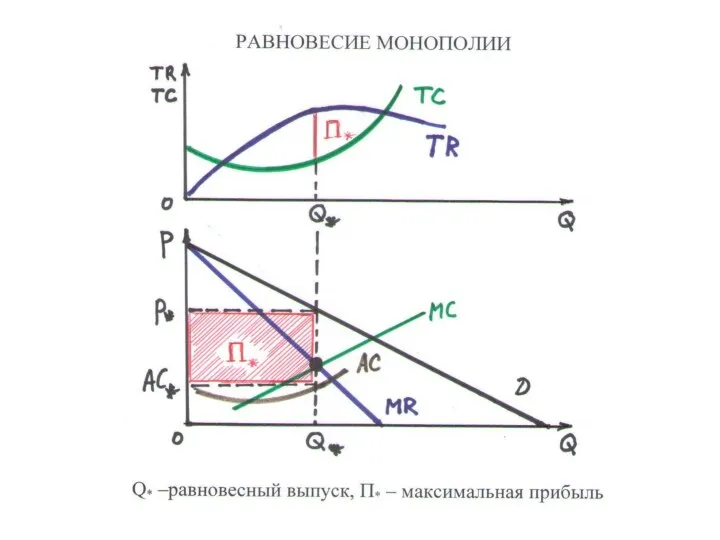
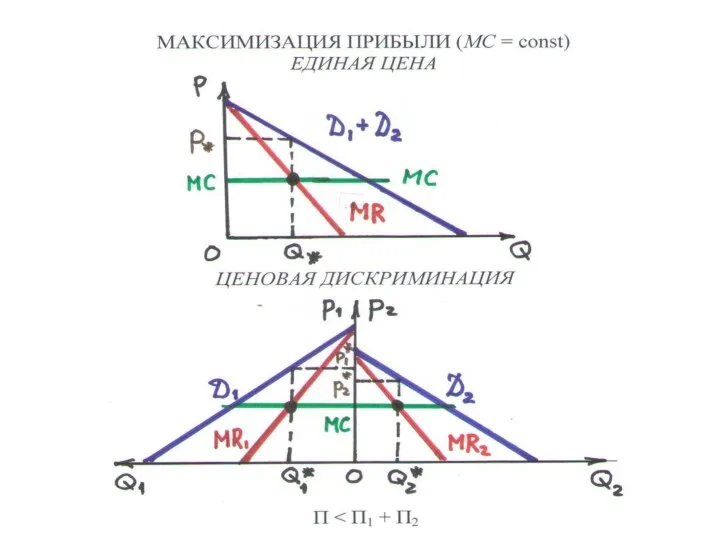
Слайд 132РАВНОВЕСИЕ МОНОПОЛИИ ПРИ ДИСКРИМИНАЦИИ
П(Q1,Q2) = TR1(Q1) + TR(Q2) – TC(Q1+Q2)
УСЛОВИЕ РАВНОВЕСИЯ (П

→ max) – предельные выручки в сегментах равны MC:
MR1(Q1) = MR2(Q2) = MC(Q1+Q2)
ФОРМУЛА СКИДОК:
p1/p2 = (1–1/E2)/(1–1/E1)
p1 и p2 – цены, E1 и E2 – эластичность спроса
ВЫВОД: Равновесная цена меньше у покупателя с большей эластичностью спроса
Слайд 133ВЫВОД ФОРМУЛЫ СКИДОК:
MR1 = p1(1–1/E1), MR2 = p2(1–1/E2)
MR1 = MR2 p1(1 –

1/E1) = p2(1 – 1/E2)
p1/p2 = (1 – 1/E2)/(1 – 1/E1)
ЗАДАЧА. Взрослые: E1 = 2. Дети: E2 = 3. MC = 10. Найти равновесные цены.
РЕШЕНИЕ. p1/p2 = (1–1/3)/(1–1/2) = 1,33
p2/p1 = 0,75 → Скидка = 25%
MR1 = МС → p1(1 – 1/2) = 10
ИТАК, р1 = 20, р2 = 0,75·20 = 15
Слайд 136ДИСКРИМИНАЦИЯ: ПРИМЕР. ДАНО:
Q1 = 10 – p1 Q2 = 20 –

p2 TC = 4Q
1) TR1 = p1Q1 = (10 – Q1)Q1
2) MR1 = TR1' = 10 – 2Q1 = 4 → Q1 = 3
3) MR2 = TR2' = 20 – 2Q2 = 4 → Q2 = 8
4) p1 = 10 – 3 = 7 → TR1 = 7×3 = 21
5) p2 = 20 – 8 = 12 → TR2 = 12×8 = 96
6) TC = 4(Q1 + Q2) = 4×11 = 44
7) П = TR – TC = (21 + 96) – 44 = 73
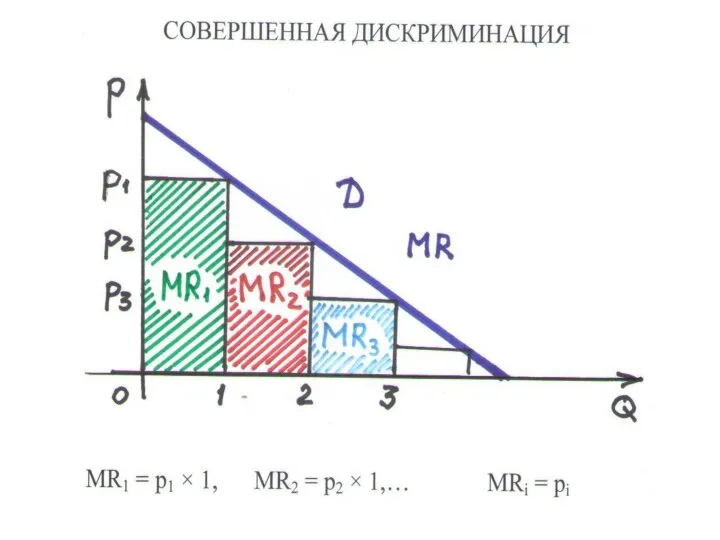
Слайд 137СОВЕРШЕННАЯ ЦЕНОВАЯ ДИСКРИМИНАЦИЯ
– потребительский излишек на рынке равен нулю
УСЛОВИЕ: монополист знает кривую

спроса каждого покупателя и устанавливает для него цену, равную максимальной цене спроса (pi )
ВЫРУЧКА : TRn = p1 + … + pn p1 ≥ … ≥ pn
ВЫВОД 1: т.к MRi = pi , то MR = p
- как в случае конкурентной фирмы
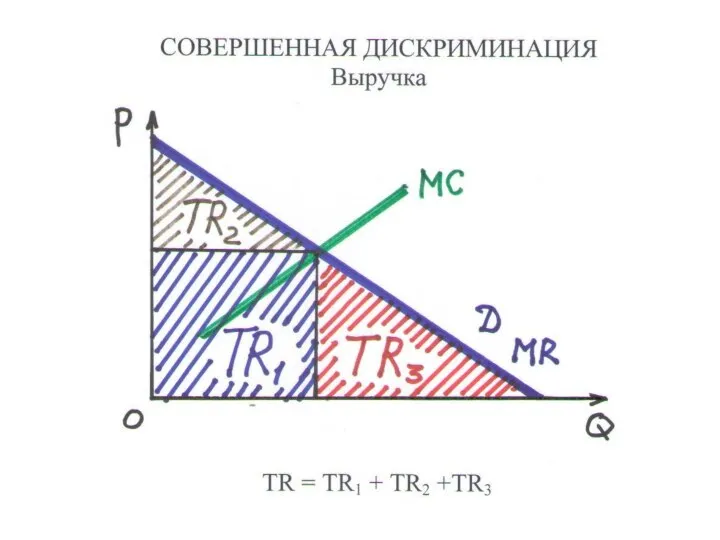
ВЫВОД 2: Равновесие при совер. дискриминации – в точке равновесия совершенного рынка
ВЫВОД 3. Равновесная выручка: TR =TRC + S
TRC, S –выручка и излишек на соверш.рынке
Слайд 141ОТЛЫНИВАНИЕ РАБОТНИКОВ (Доп. 4)
КОЭФФИЦИЕНТ ТРУДОВЫХ УСИЛИЙ (e) – часть рабочего времени, которую

работник трудится
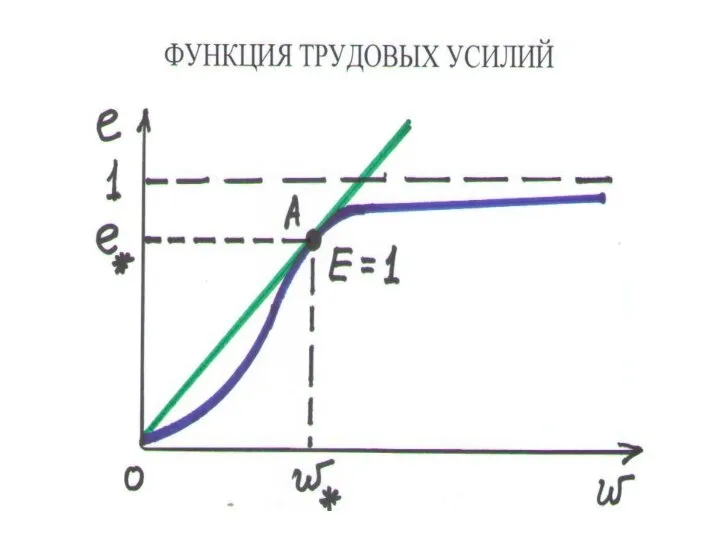
ФУНКЦИЯ ТРУДОВЫХ УСИЛИЙ e(w) – зависимость e от ставки зарплаты w (e≤1)
• возрастает и стремится к 1 при росте w
ФАКТИЧЕСКИЕ ЗАТРАТЫ ТРУДА – произведение e и оплаченного рабочего времени L: Lf = e·L
ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ – зависимость выпуска Р от фактических затрат труда P(Lf) = P(e(w)L)
ПРИБЫЛЬ: π = pP(e(w)L) – wL
Слайд 142РАВНОВЕСИЕ ПРИ ОТЛЫНИВАНИИ
– прибыль максимальна
УСЛОВИЕ РАВНОВЕСИЯ 1: E = 1
•

Эластичность функции е равна 1
• Касательная к графику е пересекает начало координат
СЛЕДСТВИЕ. Равновесный коэффициент трудовых усилий меньше 1
УСЛОВИЕ РАВНОВЕСИЯ 2: w = e·pMPL
СЛЕДСТВИЕ. Равновесная (эффектив- ная) ставка зарплаты меньше чем у добросовестных работников, т.к. e≤1
Слайд 144ЭФФЕКТИВНАЯ ЗАРПЛАТА: ПРИМЕР
ДАНО: P = 2L0,5, p = 1, e = 1–2/w
1.

ЭЛАСТИЧНОСТЬ: E = (w/e)e' = 2/(w – 2)
2. ОПТИМАЛЬНАЯ СТАВКА ЗАРПЛАТЫ:
Е = 1, Е = 2/(w – 2) = 1 → w* = 4
3. e* = 1 – 2/4 = 0,5 (50%)
4. ОПТИМАЛЬНАЯ ПРОДУКТИВНОСТЬ ТРУДА:
w* = e*pMPL, 4 = 0,5·1·L0,5 → MPL = 8
5. ОПТИМАЛЬНАЯ ЧИСЛЕННОСТЬ ПЕРСОНАЛА:
MPL = P' = L0,5 = 8 → L* = 64
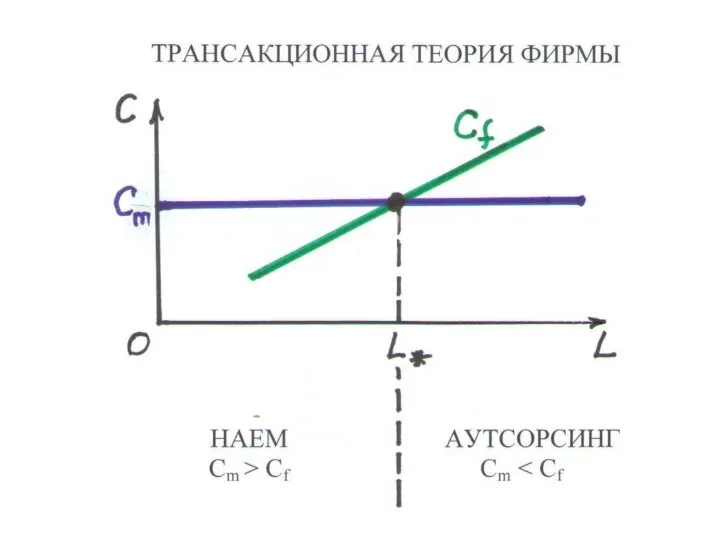
Слайд 145ТРАНСАКЦИОННАЯ ТЕОРИЯ ФИРМЫ (3.4)
РЫНОЧНАЯ ТРАНСАКЦИЯ (внешняя) – сделка с внешними агентами
ЗАТРАТЫ на

нее неизменно равны Сm (аутсорсинг )
НЕРЫНОЧНАЯ ТРАНСАКЦИЯ (внутренняя) – сделка с внутренними агентами.
ЗАТРАТЫ на нее Сf растут с увеличением объема фирмы (трудовой договор)
УСЛОВИЕ РАСШИРЕНИЯ ФИРМЫ: внутренние затраты меньше внешних затрат: Cf < Cm
ОПТИМАЛЬНЫЙ РАЗМЕР ФИРМЫ – равенство внешних и внутренних трансакционных затрат: Cf = Cm
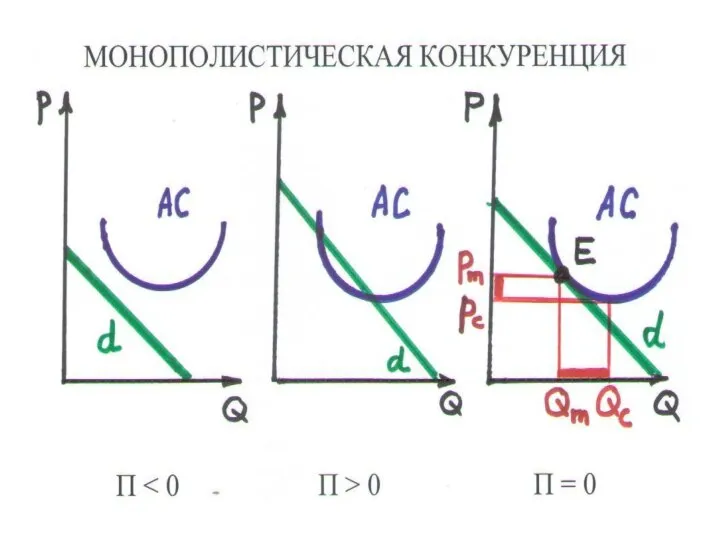
Слайд 148МОНОПОЛИСТИЧЕСКАЯ КОНКУРЕНЦИЯ (4.5)
– конкурируют производители близких заменителей (ЕXY ≈ ∞)
ДИФФЕРЕНЦИАЦИЯ ТОВАРА –

различие товаров по наблюдаемому параметру: действительная (вкус), искусственная (имидж)
ОБЩИЕ ЧЕРТЫ С СОВЕРШЕННЫМ РЫНКОМ
• большое количество продавцов и покупателей
• свободный вход и выход с рынка
• фирмы применяют одинаковые технологии
• кривые спроса на продукт фирмы одинаковы
ОБЩИЕ ЧЕРТЫ С МОНОПОЛИЕЙ
• фирма обладает рыночной властью
• фирма производит уникальный продукт
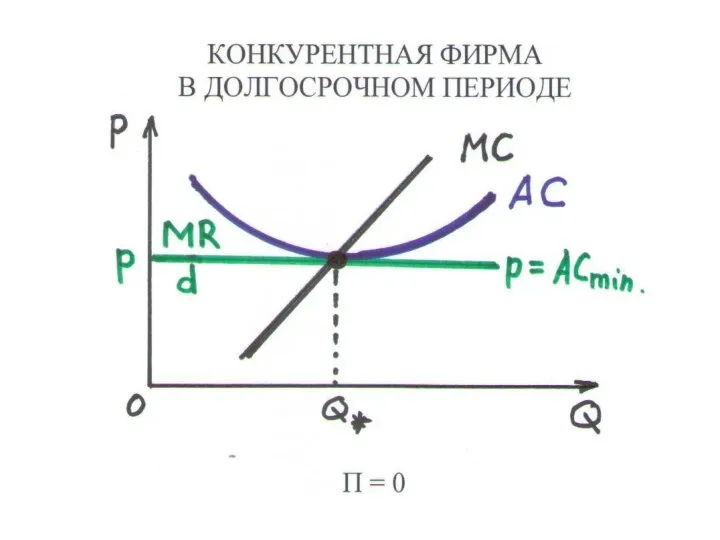
Слайд 149МОНОПОЛИСТИЧЕСКАЯ КОНКУРЕНЦИЯ
РАВНОВЕСИЕ В ДОЛГОСРОЧНОМ ПЕРИОДЕ
• единая долгосрочная кривая средних издержек (LRAC) –

единая технология
• кривая спроса на продукт фирмы d касается LRAC
• единая цена на продукты всех фирм превышает минимум средних издержек
• суммарный выпуск фирм меньше, чем при совершенной конкуренции
• прибыль каждой фирмы равна нулю
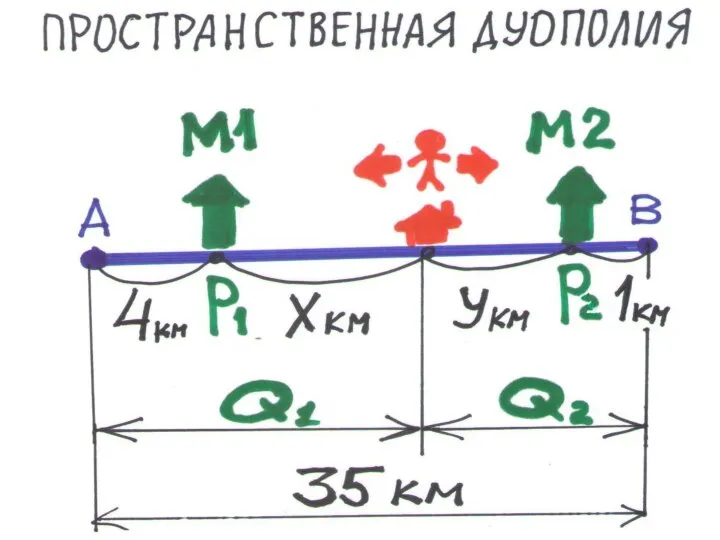
Слайд 151ОЛИГОПОЛИЯ (4.5)
– каждая фирма способна влиять на рыночную цену (несколько крупных

фирм)
СВОЙСТВА
• взаимозависимость поведения фирм
• кривая спроса на продукцию фирмы зависит от поведения конкурентов
ДУОПОЛИЯ – на рынке две фирмы
• КООПЕРИРОВАННАЯ – фирмы действуют согласованно (сговор)
• НЕКООПЕРИРОВАННАЯ – фирмы действуют независимо (нет сговора)
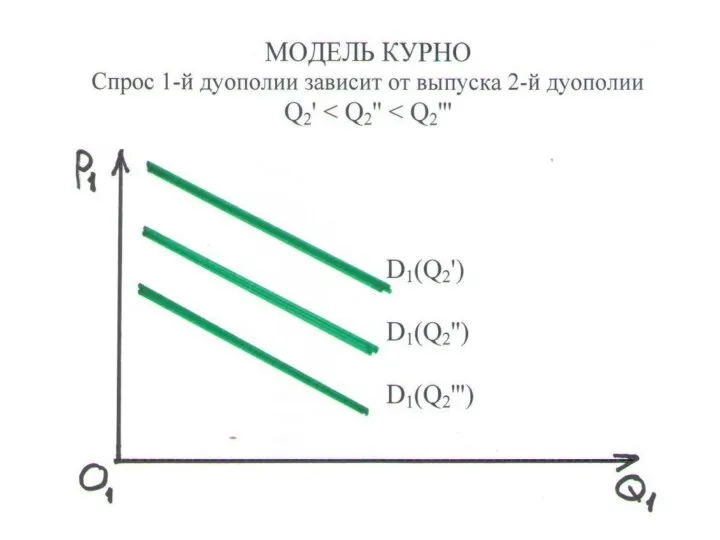
Слайд 152МОДЕЛЬ КУРНО
• некооперированная дуополия, FC = 0, MC = c
• каждая

дуополия максимизирует прибыль, считая выпуск другой заданным
• рыночный спрос зависит от Q – суммарного объема продаж:
p = a – bQ, p = a – b(Q1 +Q2)
Кривая спроса 1й дуополии (в скобках-конст.)
p = (a – bQ2) – bQ1
• при Q2 = 0 совпадает с кривой рыночного спроса
• с ростом Q2 сдвигается влево
ВЫРУЧКА 1-й дуополии при заданном Q2
TR1 = pQ1 = [(a – bQ2) – bQ1]Q1
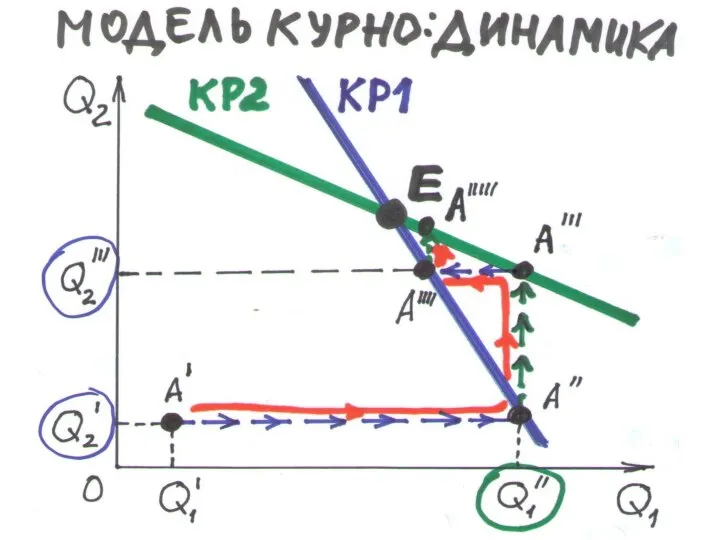
Слайд 154МОДЕЛЬ КУРНО. РАВНОВЕСИЕ
ПРИБЫЛЬ 1-Й ДУОПОЛИИ
П1(Q1) = TR1 – cQ1 = aQ1 –

b(Q1)2 – bQ1Q2 – cQ1
РАВНОВЕСИЕ 1: П1'(Q1) = 0
a – 2bQ1– bQ2 –c =0, Q1 = (a – c)/2b – Q2/2
КРИВАЯ РЕАГИРОВАНИЯ 1 – выпуски (Q1;Q2), которые удовлетворяют условию равновесия 1.
КРИВАЯ РЕАГИРОВАНИЯ 2 – выпуски (Q1;Q2), которые удовлетворяют условию равновесия 2:
Q2 = (a – c)/2b – Q1/2
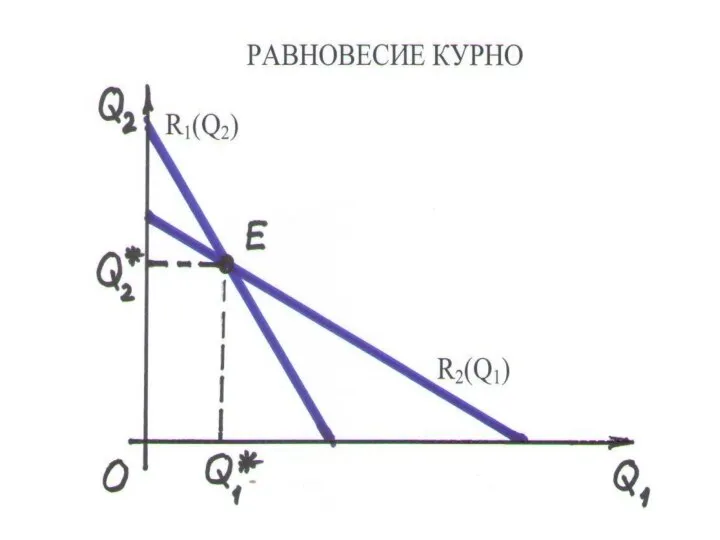
РАВНОВЕСИЕ КУРНО – выполняются условия равновесия 1 и 2, кривые реагирования 1 и 2 пересекаются: Q1*= Q2*= (a – c)/3b
Слайд 156РАВНОВЕСИЕ КУРНО И МОНОПОЛИЯ
ПРИБЫЛЬ МОНОПОЛИИ: П = TR–TC = (p–c)Q
П = (a

– bQ – c)Q, П = aQ – bQ2 – cQ
РАВНОВЕСИЕ МОНОПОЛИИ: П'(Q) = 0
a – 2bQ – c = 0, QM = (a – c)/2b
СУММА РАВНОВЕСНЫХ ВЫПУСКОВ КУРНО: QK = 2·(a – c)/3b QK > QM
ВЫВОД. При объединении дуополий (монополизации) суммарный выпуск сократится, а рыночная цена вырастет
Слайд 158МОДЕЛЬ КУРНО: ПРИМЕР. ДАНО:
p = 200 – 2Q, c1 = 40,

c2 = 80, FC = 0
СПРОС 1-й: p1 = 200 – 2(Q1 + Q2)
ВЫРУЧКА 1-й: TR1 = p1Q1 = (200 – 2Q1 – 2Q2)Q1
ПРИБЫЛЬ 1-й: П1 = TR1 – TC1 = TR1 − 40Q1 =
= 200Q1–2Q12– 2Q2Q1– 40Q1 = 160Q1 – 2Q12– 2Q2Q1
П1 → max: (TR1)'Q1 = 0. Кривая реагирования 1-й:
160 – 4Q1– 2Q2 = 0 → Q1 = 40 – 0,5Q2
Кривая реагирования 2-й: Q2 = 30 – 0,5Q1
РЕШАЕМ Q1=33,3, Q2=13,3, p=200–2·46,6=106,7
• ИЗДЕРЖКИ 1й МЕНЬШЕ → ВЫПУСК 1й БОЛЬШЕ
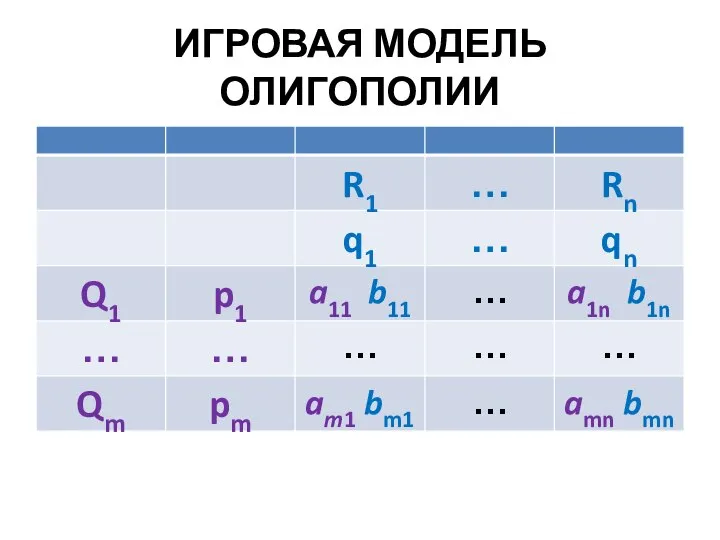
Слайд 159ИГРОВАЯ МОДЕЛЬ ОЛИГОПОЛИИ (4.5)
ВЫПУСКИ ФИРМЫ 1: Q1, …, Qm
СТРАТЕГИЯ ФИРМЫ 1

: (p1, …, pm)
pi – вероятность выпуска Qi (∑pi = 1)
ВЫПУСКИ ФИРМЫ 2: R1, …, Rn
СТРАТЕГИЯ ФИРМЫ 2: (q1, …, qn)
qj – вероятность выпуска Rj (∑qj = 1)
ПРИБЫЛЬ Ф.1 при выпусках Qi и Rj равна aij
ПРИБЫЛЬ Ф.2 при выпусках Qi и Rj равна bij
ПЛАТЕЖНЫЕ МАТРИЦЫ: A = {aij}, B = {bij}
Слайд 160ПРАВИЛА ИГРЫ (4.6)
КАЖДАЯ ФИРМА НЕЗАВИСИМО ОТ ДРУГОЙ ВЫБИРАЕТ ОБЪЕМ ВЫПУСКА С ЦЕЛЬЮ

МАКСИМИЗАЦИИ ПРИБЫЛИ
НАПРИМЕР: 1-Я ФИРМА – 4-Й ВЫПУСК
2-Я ФИРМА – 3-Й ВЫПУСК
ТОГДА ПРИБЫЛЬ: 1-Й ФИРМЫ = a43
2-Й ФИРМЫ = b43
ВЫБОР СОВЕРШАЕТСЯ МНОГОКРАТНО
Слайд 163ОСТОРОЖНАЯ СТРАТЕГИЯ
МИНИМАЛЬНАЯ ПРИБЫЛЬ ФИРМЫ 1 при выпуске Qi равна минимальному элементу i-й

строки – aimin
ГАРАНТИРОВАННАЯ ПРИБЫЛЬ ФИРМЫ 1 (МАКСИМИН) – максимальное значение из минимумов по всем строкам:
a0 = max(aimin) = max min aij
ОСТОРОЖНАЯ СТРАТЕГИЯ ФИРМЫ 1 : рio = 1
i0 – соответствующая строка матрицы А
При выпуске Qi0 прибыль не меньше a0
Слайд 164ОСТОРОЖНАЯ СТРАТЕГИЯ 2-Й ФИРМЫ
МИНИМАЛЬНАЯ ПРИБЫЛЬ ФИРМЫ 2 при выпуске Rj равна минимальному

элементу j-го столбца – bjmin
ГАРАНТИРОВАННАЯ ПРИБЫЛЬ ФИРМЫ 2 (МАКСИМИН) – максимальное значение из минимумов по всем столбцам:
b0 = max(bjmin) = max min bij
ОСТОРОЖНАЯ СТРАТЕГИЯ ФИРМЫ 2 : qjo = 1
j0 – соответствующий столбец матрицы В
При выпуске Qj0 прибыль не меньше b0
Слайд 165ОСТОРОЖНЫЕ СТРАТЕГИИ:
ПРИМЕР: i0 = 2 j0 = 3 a0 = 5
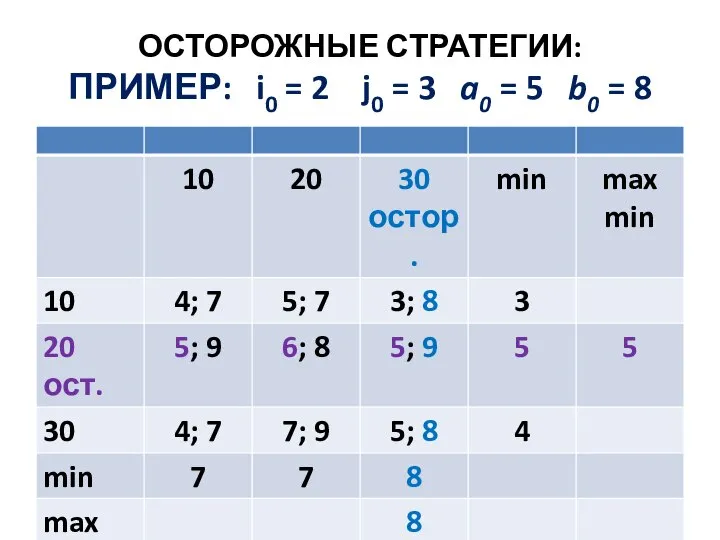
b0 = 8
Слайд 166ИГРОВОЕ РАВНОВЕСИЕ (базовые понятия)
РАВНОВЕСНАЯ СТРАТЕГИЯ – отклонение от нее влечет снижение прибыли,

если обе фирмы следуют равновесным стратегиям
S1* = (p1*, …, pm*) S2* = (q1*, …, qn*)
• метод их расчета – в курсе «Теория игр»
РАВНОВЕСНАЯ ПРИБЫЛЬ – средняя прибыль при равновесных стратегиях (a* и b*)
Если 1-я стратегия неравновесная, а 2-я равновесная (S1 ≠ S1*, S2 = S2*), то
aсредняя ≤ а*, bсредняя ≥ b*
Слайд 167ИГРА С НУЛЕВОЙ СУММОЙ
− сумма прибылей фирм всегда равна 0
aij + bij

= 0 bij = − aij В = - А
ГАРАНТИРОВАННАЯ ПРИБЫЛЬ ФИРМ:
а0 = max min aij b0 = - min max aij
ЦЕНА ИГРЫ – равновесная прибыль 1й фирмы,
лежит между максимином и минимаксом
max min aij ≤ a* ≤ min max aij
СПРАВЕДЛИВАЯ ИГРА: a* = b* = 0
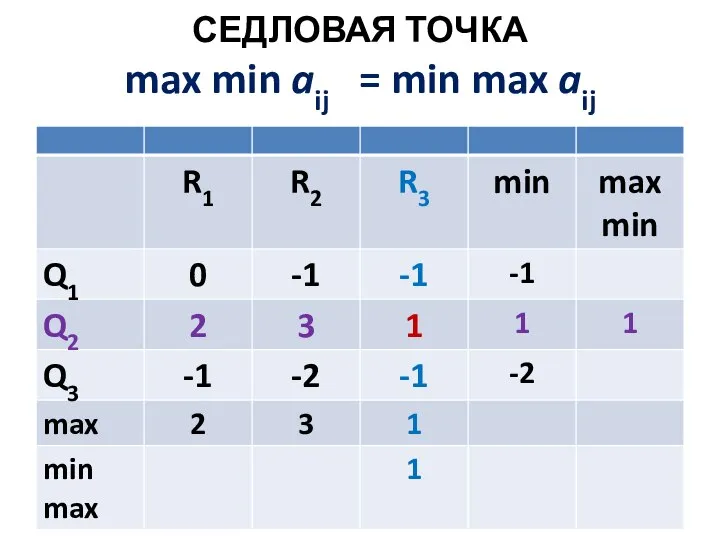
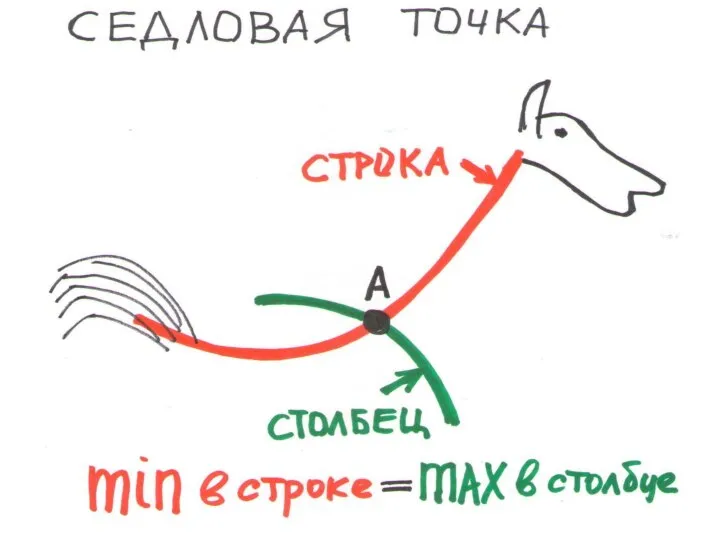
Слайд 168СЕДЛОВАЯ ТОЧКА
max min aij = min max aij
Слайд 171РЫНОК ТРУДА ОСОБЕННОСТИ
НЕОТЧУЖДАЕМОСТЬ – труд неотделим от работника
НЕОДНОРОДНОСТЬ – труд работников различен
ДИФФЕРЕНЦИРОВАННАЯ

ЦЕНА – следствие неоднородности и мотивации
НЕДЕЛИМОСТЬ – рабочий день фиксирован
АСИММЕТРИЯ ИНФОРМАЦИИ – нанимателю сложно определить продуктивность работника
НЕМОБИЛЬНОСТЬ – следствие регистрации, отсутствия рынка жилья
ВЫСОКИЕ ТРАНСАКЦИОННЫЕ ИЗДЕРЖКИ – затраты на прием, наем, оценку качества труда
Слайд 172СПРОС НА ТРУД. КОНКУРЕНТНАЯ ФИРМА (4.4)
СПРОС НА ТРУД – объем труда, при

котором прибыль максимальна π(L) = pP – wL
π – прибыль, p – цена, Р –выпуск,
w – ставка зарплаты, L – затраты труда
РАВНОВЕСИЕ π' = 0 pP' – w = 0 w = pMPL
Кривая спроса на труд конкурентной фирмы совпадает с графиком стоимости предельного продукта труда
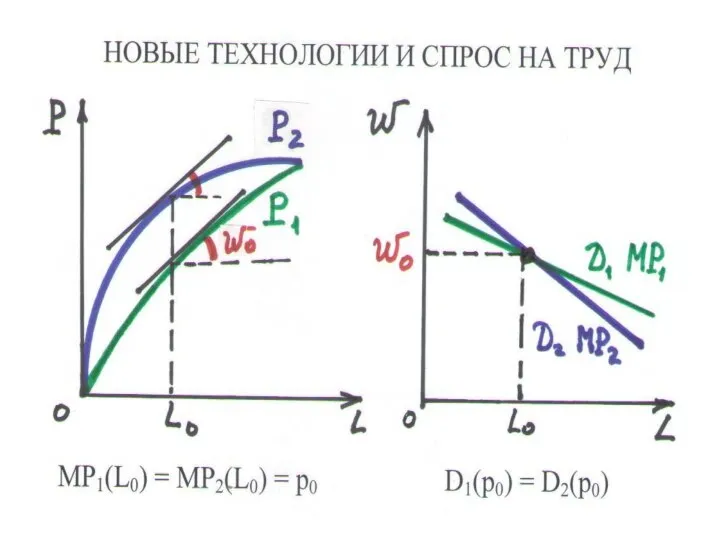
НЕЦЕНОВЫЕ ФАКТОРЫ СПРОСА
• с ростом цены продукта кривая сдвигается вправо
• внедрение новой технологии может привести к сдвигу кривой спроса вправо или влево
Слайд 174СПРОС НА ТРУД МОНОПОЛИИ (4.5)
ПРЕДЕЛЬНЫЙ ДЕНЕЖНЫЙ ПРОДУКТ ТРУДА –
прирост выручки при росте

затрат труда на 1 ед.
MRPL = ΔTR:ΔL = TR'(L)
• MRPL = (ΔTR/ΔQ) · (ΔQ/ΔL) = MR · MPL
• MRPL определяется функциями D(p) и P(L)
• MRPL падает с ростом L, т.к. падают MR и MPL
• MRPL = pMPL для конкурентной фирмы
СПРОС НА ТРУД – затраты труда при равновесии
π'(L) = 0 TR'(L) – w = 0 w = MRPL
Кривая спроса на труд совпадает с кривой MRPL
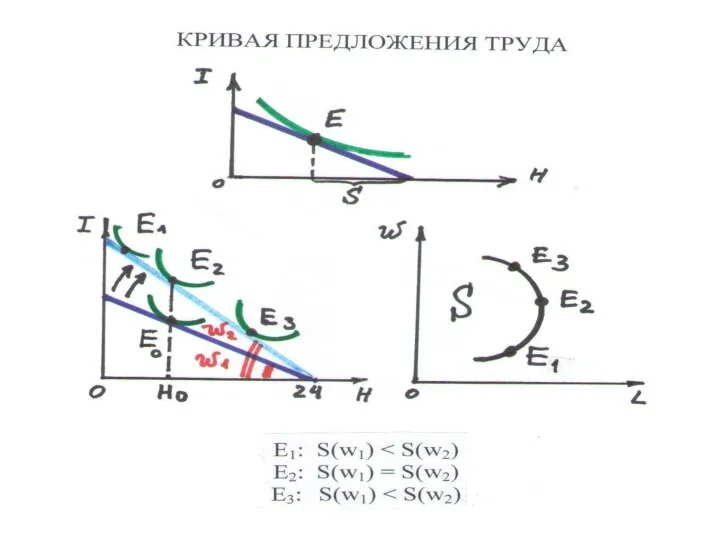
Слайд 175ПРЕДЛОЖЕНИЕ ТРУДА
ИНДИВИДУАЛЬНОЕ ПРЕДЛОЖЕНИЕ ТРУДА – объем труда, который работник желает и способен

продать при данной ставке зарплаты
РЫНОЧНОЕ ПРЕДЛОЖЕНИЕ ТРУДА – объем труда, который все работники желают и способны продать при данной ставке зарплаты
ФУНКЦИЯ ПРЕДЛОЖЕНИЯ ТРУДА S(w) – зависимость объема предложения труда от ставки зарплаты
ОСОБЕННОСТЬ S(L) – возрастает, затем убывает
Слайд 176ФУНКЦИЯ ПОЛЕЗНОСТИ РАБОТНИКА U(H, I)
– зависимость полезности от досуга Н и дохода

I
• U ≥ 0 • U(0,0)=0 • MUH > 0 • MUI > 0
ПРЕДЕЛЬНАЯ ПОЛЕЗНОСТЬ ДОСУГА:
MUH = ΔU:ΔH
ПРЕДЕЛЬНАЯ ПОЛЕЗНОСТЬ ДОХОДА:
MUI = ΔU:ΔI
КРИВАЯ БЕЗРАЗЛИЧИЯ – наборы(H, I) с равной полезностью
• нисходящая кривая
Слайд 177ПРЕДЕЛЬНАЯ НОРМА ЗАМЕЩЕНИЯ
– на столько рублей необходимо увеличить доход при уменьшении

досуга на 1 час при неизменной полезности
MRS = ΔI : ΔH = MUH : MUI
• положительная величина
• относительная ценность досуга, выраженная в рублях на 1 час досуга
• уменьшается с ростом досуга
• равна тангенсу угла наклона касательной к кривой безразличия
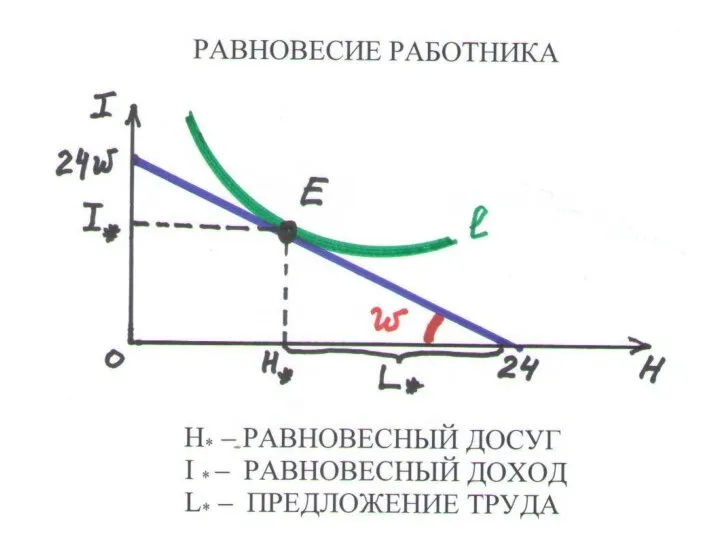
Слайд 178РАВНОВЕСИЕ РАБОТНИКА
– максимум полезности при бюджетном ограничении
I = w(24 – H) I

+ wH = 24w
wH и 24w – упущенный и максимальный доход
РАВНОВЕСИЕ – кривая безразличия касается бюджетной линии: MRS = w
ПРЕДЛОЖЕНИЕ ТРУДА = равновесные затраты труда
НЕЦЕНОВЫЕ ФАКТОРЫ ПРЕДЛОЖЕНИЯ
ЭФФЕКТ ЗАМЕЩЕНИЯ – при низких ставках доход ценнее досуга. Работник увеличивает предложение
ЭФФЕКТ ДОХОДА – при высоких ставках досуг ценнее дохода. Работник снижает предложение труда
ВЫВОД. С ростом ставки зарплаты предложение труда сначала растет, затем снижается
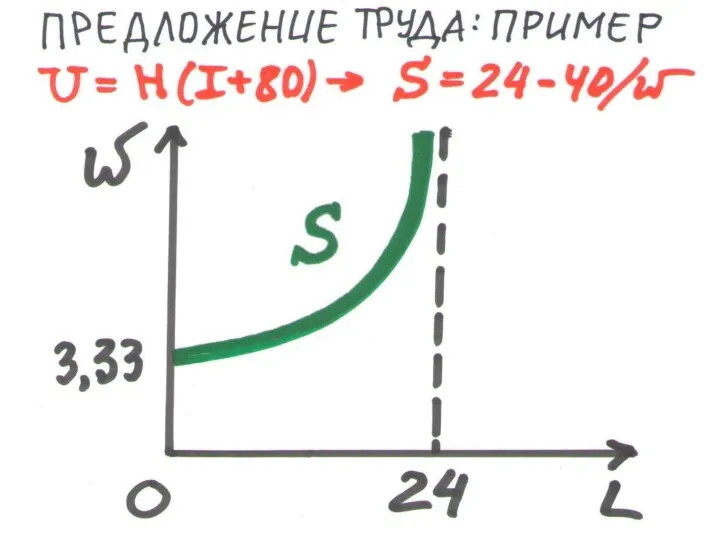
Слайд 181ПРЕДЛОЖЕНИЕ ТРУДА: ПРИМЕР
ДАНО: U = H(I+80). НАЙТИ S(w). РЕШЕНИЕ
БЮДЖ.ОГРАНИЧЕНИЕ: I = 24w

– wH
ПОДСТАВИМ В U: U = H(24w – wH + 80)
ДИФФ-ЦИРУЕМ: U' = 24w – 2wH + 80 = 0
ВЫРАЖАЕМ: H = 12 + 40/w
L = 24 – H = 24 – 40/w S = 24 – 40/w
МИНИМАЛЬНАЯ ЦЕНА ПРЕДЛОЖЕНИЯ:
24 – 40/w = 0 → w = 3,33
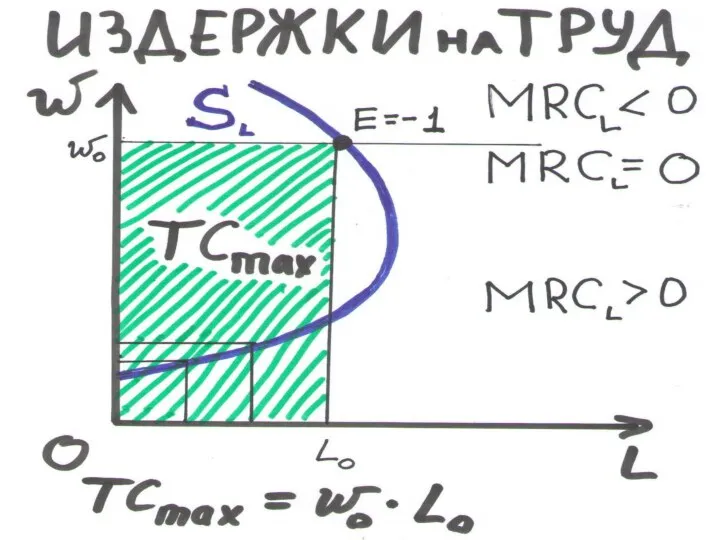
Слайд 184ИЗДЕРЖКИ НА ТРУД МОНОПСОНИИ: (4.5)
TC(L) = L·w(L)
w(L)–обратная функция к предложению

труда
ПРЕДЕЛЬНЫЕ ИЗДЕРЖКИ НА ТРУД – прирост ТС, вызванный ростом затрат труда на 1ед.
MRCL = ΔTC : ΔL = ТС'
MRCL = w +L(dw/dL) = w(1 + 1/E)
Е – эластичность S(L), часто считают Е > 0:
• Если Е = 0, то MRCL = ∞ • Е =-1, ТС–максим.
• Обычно Е > 0, и MRCL растет с ростом w
Слайд 186РАВНОВЕСИЕ ФИРМЫ НА РЫНКЕ ТРУДА
РАВНОВЕСИЕ: π'(L) = TR'(L)–TC'(L) = 0
MRPL =

MRCL
• рынок продукта совершенен:
pMPL = MRCL
• рынок труда совершенен: MRPL = w
• оба рынка совершенны: MPL = w/p Предельный продукт труда равен реальной ставке зарплаты (w/p) – столько единиц продукта зарабатывают за 1 ч
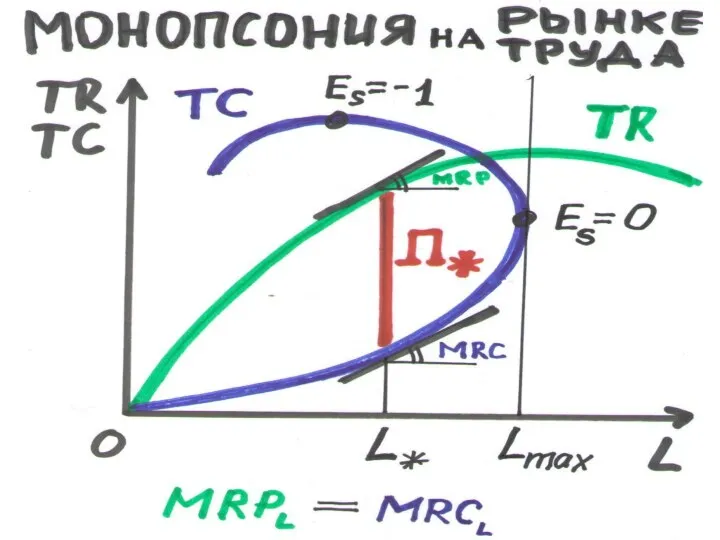
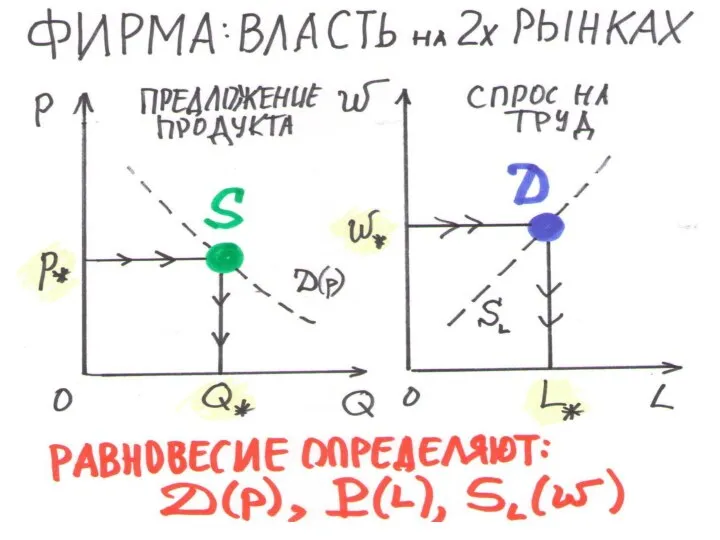
Слайд 188РАВНОВЕСИЕ МОНОПОЛИИ-МОНОПСОНИИ
1. НАЙДЕМ РАВНОВЕСНЫЕ ЗАТРАТЫ ТРУДА:
MRPL(L*) = MRCL(L*) → L*
2.НАЙДЕМ РАВНОВЕСНУЮ

СТАВКУ ЗАРПЛАТЫ
SL(w*) = L* → w*
3. РАВНОВЕСНЫЙ ВЫПУСК: P* = P(L*) → P*
4. РАВНОВЕСНАЯ ЦЕНА: D(p*) = Р* → p*
ПРЕДЛОЖЕНИЕ ТРУДА (S) – точка (p*,P*)
СПРОС НА ТРУД (D) – точка (w*,L*)
Слайд 190РЫНОК КАПИТАЛА. СТАВКА ПРОЦЕНТА
ДЕНЕЖНЫЙ КАПИТАЛ – деньги, предназначенные для получения дохода (процента)
РЫНОК

ДЕНЕЖНОГО КАПИТАЛА – рынок услуг по предоставлению ссуд (кредитов)
• покупатель – заемщик (инвесторы и др.)
• продавец – кредитор (домохозяйства и др.)
СТАВКА ПРОЦЕНТА (i) – цена денег, равная проценту по кредиту 1 руб.
С ростом ставки %: D(i) убывает, S(i) растет
РАВНОВЕСИЕ D(i*) = S(i*)
В РАВНОВЕСИИ ОБЪЕМ КРЕДИТОВ МАКСИМАЛЕН
Слайд 191ДИСКОНТИРОВАНИЕ
ДОХОДЫ: через 1 год – R1, через 2 года – R2
помещаются

на срочный вклад под i % годовых
ТЕКУЩАЯ ДИСКОНТИРОВАННАЯ СТОИМОСТЬ − текущий эквивалент будущего потока доходов
PDV = R1/(1 + i) + R2 /(1 + i)2
• Вклад в сумме PDV через 2 года обеспечит ту же выручку, что и доходы R1, R2
ДИСКОНТИРУЮЩИЙ МНОЖИТЕЛЬ: αk = 1/(1 + i)k
PDV = α1R1 + α2R2
• Чем позже получен доход, тем меньше αk
Слайд 192АННУИТЕТ
− постоянный бесконечный годовой доход R
PDV = kR + k2R +

k3R + …
где k = 1/(1 + i)
PDV – сумма бесконечной геом. прогрессии
PDV = R : i
ЦЕНА КВАРТИРЫ. Годовая аренда=240 тыс.
руб. Ставка 5%. Тогда цена квартиры равна
PDV=240:0,05=4800 т.руб.(4,8 млн.р.)
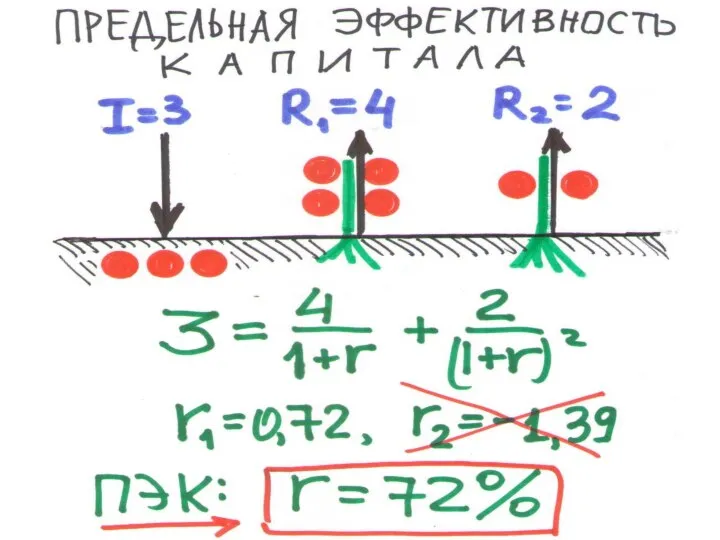
Слайд 193ИНВЕСТИЦИИ
– затраты ресурсов для получения доходов
ИНВЕСТИЦИОННЫЙ ПРОЕКТ –инвестиции (I ) и порожденный

ими поток доходов:
I → R1, R2, …
ЧИСТАЯ ДИСКОНТИРОВАННАЯ СТОИМОСТЬ
NPV = PDV – I
• если NPV > 0, то проект выгоден
• если NPV ≤ 0, то проект не выгоден
ПРИВЕДЕННАЯ ДОХОДНОСТЬ:
r = NPV : I × 100%
Слайд 194Пример. I =5, R1=5, R3=4, i=6%. r =?
|_______|_______|_______|
I → R1 0

R3
PDV = 3/1,06 + 0 + 4/1,063 = 6,19
r = PDV/I –1 =6,19/5–1=0,238(23,8%)
ВЫРУЧКА В КОНЦЕ 3-го ГОДА:
ПРОЕКТ: TR = 3∙1,062 + 4 = 7,37
ВКЛАД: TR=PDV(1+i)3=6,19∙1,063=7,37
Слайд 196ПРЕДЛОЖЕНИЕ СБЕРЕЖЕНИЙ (Доп.2)
– равновесный объем сбережений домохозяйства при данной ставке %
РАВНОВЕСИЕ СБЕРЕГАЮЩЕГО

ДОМОХОЗЯЙСТВА – полезность (U) максимальна при межвременном ограничении
U(C1,C2) → max C2 = (1 + i)·(I – C1)
• потребление в молодости равно C1
• доход в молодости равен I
• сбережение в молодости равно I – C1
• доход в старости равен нулю
• потребление в старости (C2 ) = сбережения + %
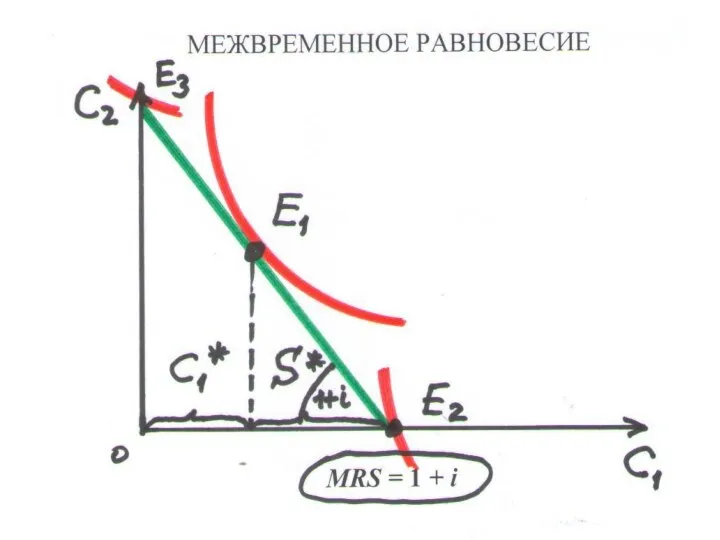
Слайд 197ПРЕДЛОЖЕНИЕ СБЕРЕЖЕНИЙ – разность дохода в молодости и равновесного потребления в молодости:

S *(i) = I – C1*(i)
УСЛОВИЕ РАВНОВЕСИЯ – предельная норма межвременного предпочтения (MRS) равна тангенсу угла наклона линии межвременного ограничения (1+ i):
MRS = MU1:MU2 = 1 + i
ФУНКЦИЯ ПРЕДЛОЖЕНИЯ S(i) ВОЗРАСТАЕТ
Слайд 199ПРЕДЛОЖЕНИЕ СБЕРЕЖЕНИЙ: КОББ-ДУГЛАС
U = C1αC2β
ПОДСТАВЛЯЕМ C2 = (1+i)(I–C1) в ФОРМУЛУ U

U(C1) = C1α(1 + i)β(I – C1)β U'(C1) = 0
C1*= I·α/(α + β) S =I·β/(α + β)
Функция Кобба-Дугласа: сбережения прямо пропорциональны коэффициенту эластичности β и не зависят от ставки %
• U = C10,3C20,7, I =50 → S =50·0,7 35
Слайд 200ПРЕДЛОЖЕНИЕ СБЕРЕЖЕНИЙ: ПРИМЕР
U = 2C10,5 + 4C20,5
ПОДСТАВЛЯЕМ: U = 2C10,5 + 4[(1

+ i)(I – C1)]0,5
ДИФФЕРЕНЦИРУЕМ: U' = 0 → C2 = 4(1 + i)2C1
ПОДСТАВЛЯЕМ: (1 + i)C1 + 4(1 + i)2C1 = (1 + i)·I
РЕШАЕМ: C1 = I·(1 + i)/(4i2 + 9i + 5)
S =I–C1 =I·(4i2+8i+4)/(4i2+9i+5)
• i = 0, S = 0,8·I • i = ∞, S = I
Слайд 201ОБЩЕСТВЕННЫЕ БЛАГА И ОБЩЕЕ БЛАГОСОСТ-НИЕ (2.4)
ВНЕШНИЕ ЭФФЕКТЫ (ЭКСТЕРНАЛИИ)
– влияние рынка на благосостояние

третьих лиц, не участвующих в производстве, потреблении или торговле товаром:
ПОЛОЖИТЕЛЬНЫЕ –благосостояние растет (книги)
ОТРИЦАТЕЛЬНЫЕ – благосостояние падает (водка)
СПОСОБЫ СОКРАЩЕНИЯ отрицательных экстерналий
1. ЗАПРЕТ на производство и потребление
2. АКЦИЗ (сигареты, алкоголь, бензин)
3. АНТИРЕКЛАМА (отказ от показа курения)
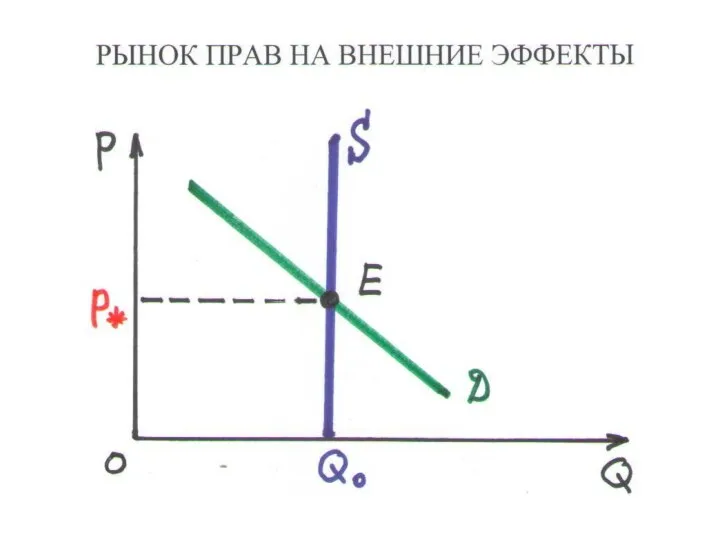
4. РЫНОК ПРАВ НА ЭКСТЕРНАЛИИ (лицензия на охоту)
Слайд 203Спос.5. ИНТЕРНАЛИЗАЦИЯ ВНЕШНЕГО ЭФФЕКТА
– превращение внешних издержек в частные
ЧАСТНЫЕ ПРЕДЕЛЬНЫЕ ИЗДЕРЖКИ (МС)

– не включают издержки на нейтрализацию внешнего эффекта (лечение курильщиков)
ВНЕШНИЕ ПРЕДЕЛЬНЫЕ ИЗДЕРЖКИ (MCвн) – затраты на нейтрализацию внешнего эффекта, порожденного дополнит. единицей продукта
ОБЩЕСТВЕННЫЕ ПРЕДЕЛЬНЫЕ ИЗДЕРЖКИ (MCоб)
MCоб = MC + MCвн
ПРИМЕР ИНТЕРНАЛИЗАЦИИ: Объединение фирм: Фирма 1 порождает эффект, Фирма 2 несет внешние издержки (химзавод и рыбохозяйство)
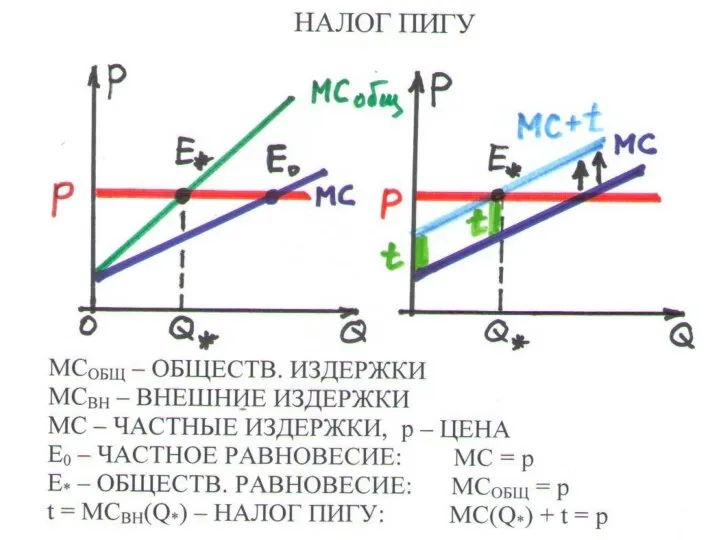
Слайд 2046. НАЛОГ ПИГУ (t ) – взимается с 1 ед. продукции, обеспечивает

общественное равновесие:
МСОБЩ (Q*)= р
• компенсирует негативные последствия экстерналий
• равен МСВНЕШ при общественно оптимальном выпуске
t = МСВНЕШ (Q*)
7. ТЕОРЕМА КОУЗА – внешний эффект может быть компенсирован без участия государства
УСЛОВИЯ ПРИМЕНЕНИЯ
• пострадавший имеет право собственности на использование ресурса, необходимого для производства «вредного» товара
• трансакционные издержки невелики
Слайд 206ОБЩЕЕ БЛАГОСОСТОЯНИЕ – набор значений индивидуального благосостояния всех членов общества): U =

(U1 , U2 , … , Un),
где n – количество членов общества
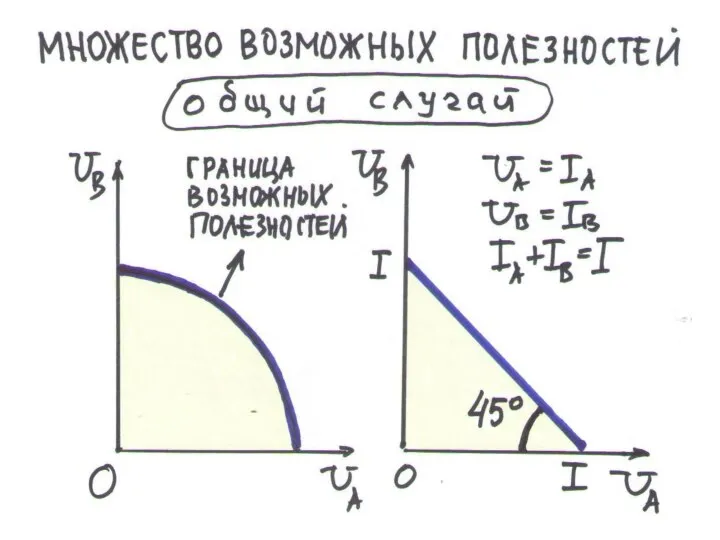
МНОЖЕСТВО ВОЗМОЖНЫХ ПОЛЕЗНОСТЕЙ – наборы значений индивидуального достояния, которые могут быть достигнуты одновременно
ГРАНИЦА ВОЗМОЖНЫХ ПОЛЕЗНОСТЕЙ – множество Парето-оптимальных состояний (точек) множества возможных полезностей
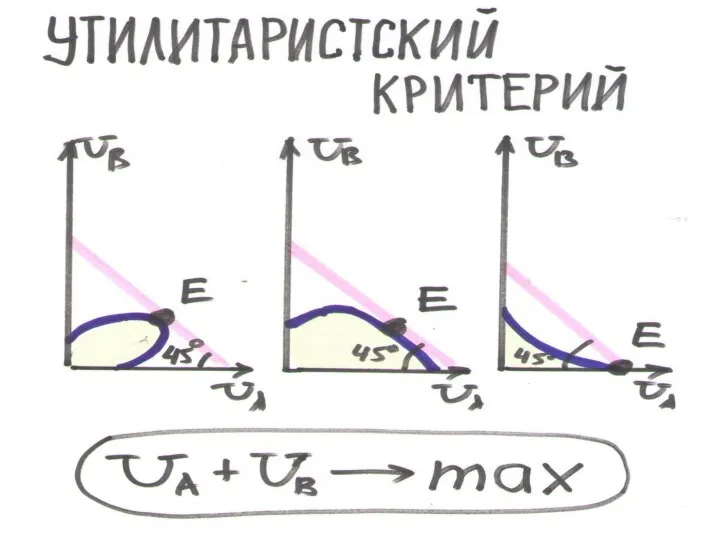
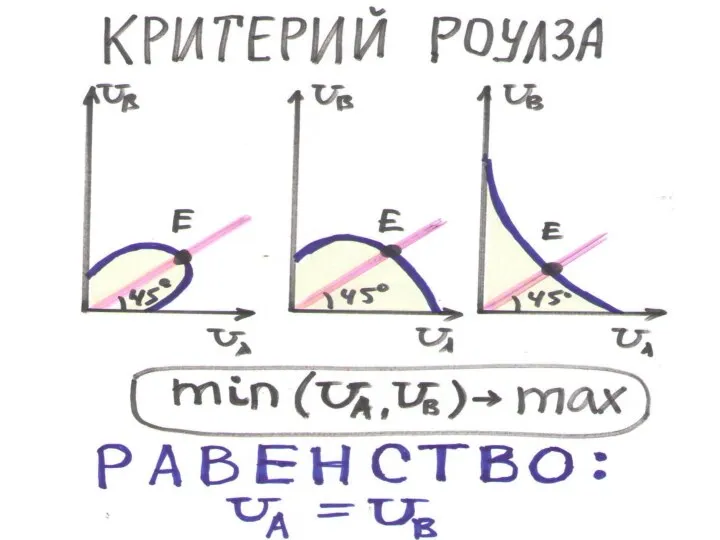
КРИТЕРИЙ БЛАГОСОСТОЯНИЯ – принцип определение наилучшего состояния на границе возможных полезностей





























![ВАЛЮТНЫЙ РЫНОК (2.2) ОБМЕННЫЙ КУРС –ЦЕНА $: p = e [руб./долл.] ОБМЕН](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1049811/slide-39.jpg)










































































































 Сущность и формы международной экономической интеграции Подготовила: Клеутина С.,группа МЭ-092
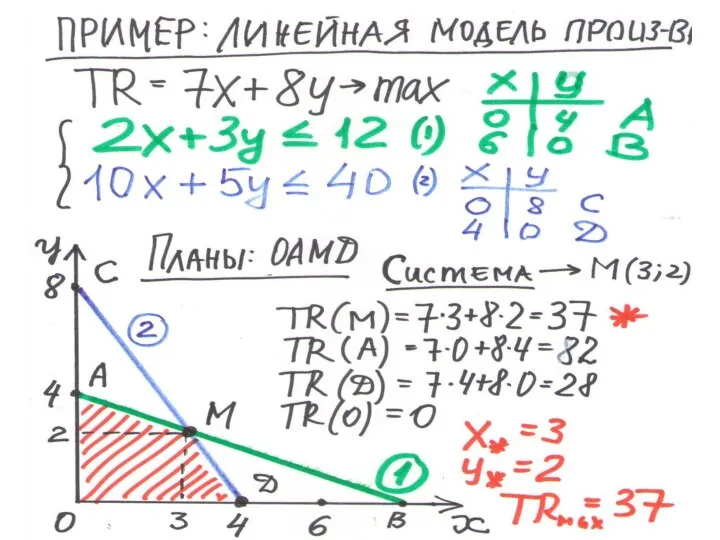
Сущность и формы международной экономической интеграции Подготовила: Клеутина С.,группа МЭ-092 Задачи определения нижних границ цен и многоступенчатого расчета маржинальной прибыли
Задачи определения нижних границ цен и многоступенчатого расчета маржинальной прибыли Сущность понятия эластичность
Сущность понятия эластичность Методические рекомендации по выполнению экономической части дипломного проекта
Методические рекомендации по выполнению экономической части дипломного проекта Россия на пути к рыночной экономике
Россия на пути к рыночной экономике Законы рынка. Издержки и условия максимизации прибыли
Законы рынка. Издержки и условия максимизации прибыли Экономический рост
Экономический рост Общее равновесие на тов и ден рынках. Кривая IS-LM
Общее равновесие на тов и ден рынках. Кривая IS-LM Экономика родного края. Удмуртская Республика
Экономика родного края. Удмуртская Республика ФИНАНСОВЫЕ РЫНКИ И ИХ ХАРАКТЕРИСТИКА Подготовила: Клеутина С., Группа МЭ-092
ФИНАНСОВЫЕ РЫНКИ И ИХ ХАРАКТЕРИСТИКА Подготовила: Клеутина С., Группа МЭ-092 Исторические условия возникновения, общая характеристика и этапы Классической школы
Исторические условия возникновения, общая характеристика и этапы Классической школы Социальные процессы в российской экономике
Социальные процессы в российской экономике Організація управлінського обліку та узагальнення даних для цілей управління. Лекція 15
Організація управлінського обліку та узагальнення даних для цілей управління. Лекція 15 Перспективы реформирования бюджетной сети
Перспективы реформирования бюджетной сети Инфраструктура интернет-экономики: понятие,развитие
Инфраструктура интернет-экономики: понятие,развитие Обмен торговля реклама (7 класс)
Обмен торговля реклама (7 класс) Экономические школы
Экономические школы Брокерская компания «Приоритет Консалтинг»
Брокерская компания «Приоритет Консалтинг» Принцип спроса и предложения
Принцип спроса и предложения Экономика фирмы. Тема 1
Экономика фирмы. Тема 1 XVI Всероссийский Фестиваль Nauka 2021
XVI Всероссийский Фестиваль Nauka 2021 Рынок как форма хозяйства. Лекции 9
Рынок как форма хозяйства. Лекции 9 Экономика фирмы. 10 класс
Экономика фирмы. 10 класс Интеграция украинской экономики в мировую хозяйственную систему
Интеграция украинской экономики в мировую хозяйственную систему Понятие, этапы развития и функции денег
Понятие, этапы развития и функции денег Задания ЕГЭ. Варианты В1
Задания ЕГЭ. Варианты В1 Рынки факторов производства и распределение доходов
Рынки факторов производства и распределение доходов Семейный бюджет
Семейный бюджет