Содержание
- 2. Пәннің мақсаты телекоммуникациялық жүйелердегі электр сигналын таратудың негізгі заңдылықтарын оқып білу. Одан басқа студенттерді электр байланынысын
- 3. Тақырып: Негізгі түсініктер мен анықтамалар. Электр сигналдарын тарату жүйесінің құрлымы
- 4. Дәрістің мақсаты: Хабарды электр сигналына түрлендіріп тарату процестерін анықтау. Электр байланыс схемасының құрлымын анықтау.
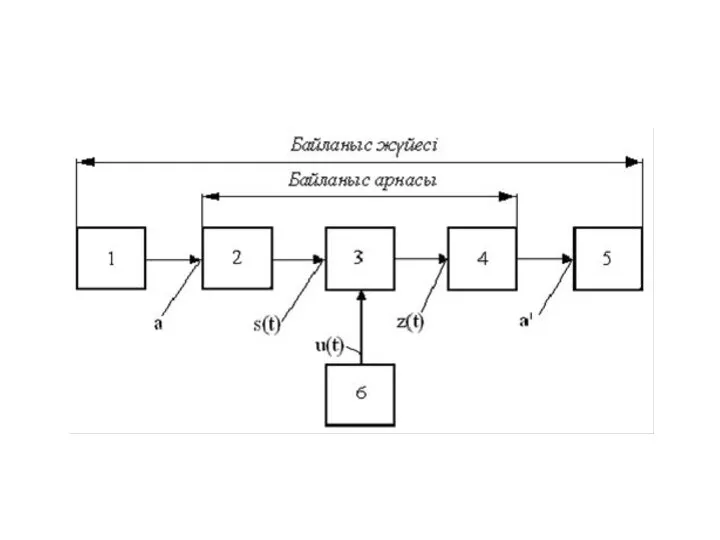
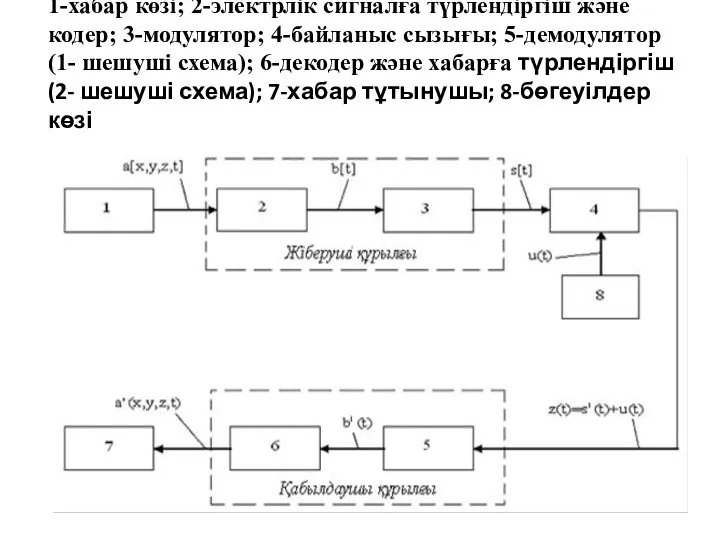
- 6. 1-хабар көзі; 2-электрлік сигналға түрлендіргіш және кодер; 3-модулятор; 4-байланыс сызығы; 5-демодулятор (1- шешуші схема); 6-декодер және
- 7. 1-хабар көзі; 2-жіберуші құрылғы; 3-байланыс сызығы; 4-қабылдаушы құрылғы; 5-хабар тұтынушы; 6-бөгеуілдер көзі
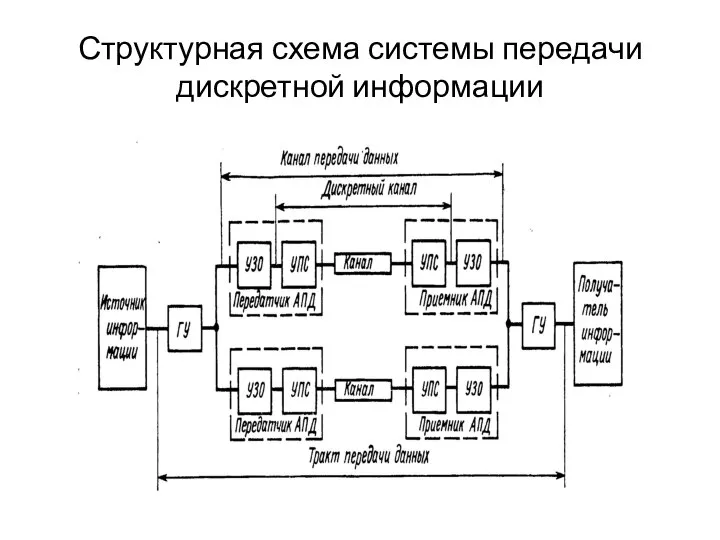
- 8. Структурная схема системы передачи дискретной информации
- 9. 1 қорек көзін форматтау и кодтау 2 видиосигдарды тарату 3 Жолақты сигналдарды тарату 4 Түзету 5
- 10. Сигнал можно классифицировать как детерминированный (при отсутствии неопределенности относительно его значения в любой момент времени) или
- 11. Периодические и непериодические сигналы Сигнал x(t) называется периодическим во времени, если существует постоянное Т0>0, такое, что
- 12. Цифровой сигнал, описываемый уровнем напряжения или тока,-сигнал (импульс - для узкополосной передачи или синусоида - для
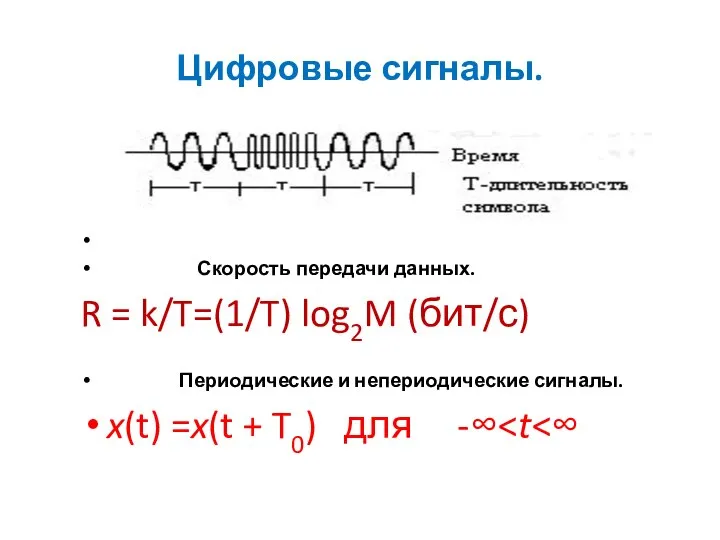
- 13. Цифровые сигналы. Скорость передачи данных. R = k/T=(1/T) log2M (бит/с) Периодические и непериодические сигналы. x(t) =x(t
- 14. Аналоговый сигнал х(t) является непрерывной функцией времени, т.е. х(t) однозначно определяется для всех t. Электрический аналоговый
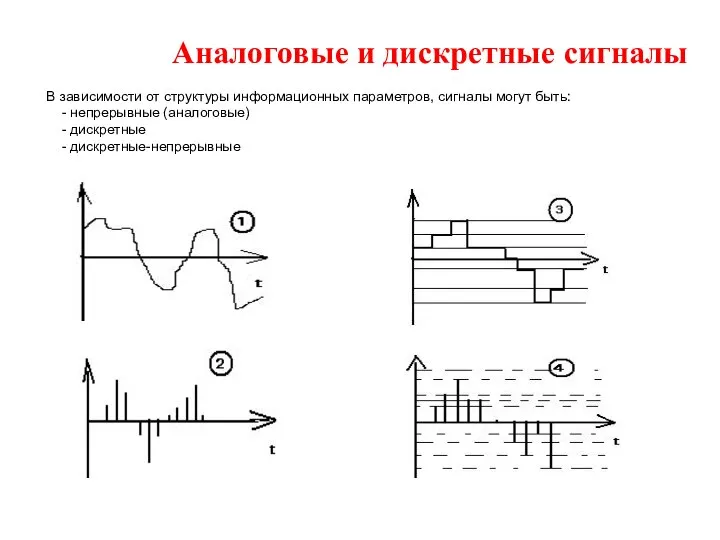
- 15. Аналоговые и дискретные сигналы В зависимости от структуры информационных параметров, сигналы могут быть: - непрерывные (аналоговые)
- 16. Производительность системы связи зависит от энергии принятого сигнала; сигналы с более высокой энергией детектируются более достоверно.
- 17. Сигналы, выраженные через энергию или мощность p{t)=ν2(t)/R p{t)=i2(t)R p{t)=x2(t) где x(t) — это либо напряжение, либо
- 18. Рассеивание энергии в течении времени для реального сигнала с мгновенной мощностью
- 19. Средняя мощность
- 20. Энергия сигнала
- 21. Мощность сигнала
- 22. Энергетический сигнал
- 23. Спектральная плотность энергии Где, X(f) — Фурье-образ непериодического сигнала x(t).
- 24. Спектральная плотность энергии x{f) является спектральной плотностью энергии (ESD) сигнала x(t). Величина
- 25. Спектральная плотность мощности. Gx(f) Спектральная плотность мощности (PSD) периодического сигнала x(t)
- 26. Автокорреляция энергетического сигнала Корреляция — это процесс согласования; автокорреляцией называется согласование сигнала с собственной запаздывающей версией.
- 27. Автокорреляция периодического сигнала значение в нуле равно энергии сигнала автокорреляция и ESD являются Фурье - образами
- 28. Спектральная плотность мощности и автокорреляция случайного процесса Основные свойства функций спектральной плотности мощности 4. Рх =
- 30. Ортогональность сигналов
- 32. Скачать презентацию














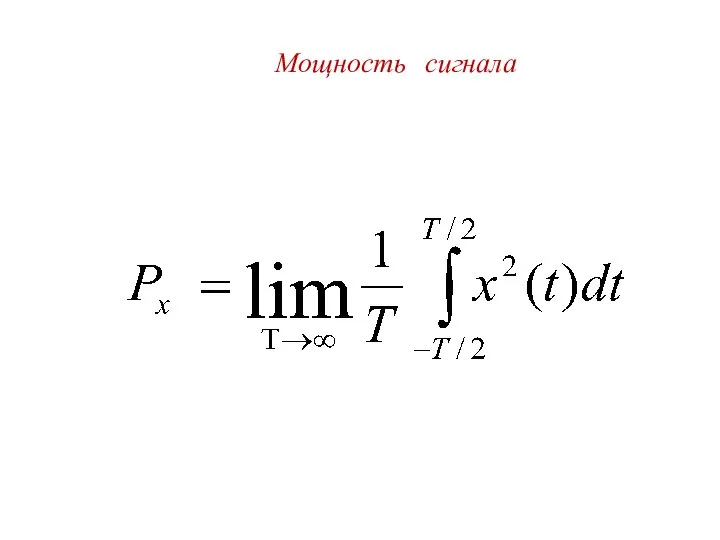








 Напрямки і показники розвитку зовнішньоекономічної діяльності в Україн
Напрямки і показники розвитку зовнішньоекономічної діяльності в Україн Соціально-економічний розвиток Наддніпрянської України у складі Російської імперії
Соціально-економічний розвиток Наддніпрянської України у складі Російської імперії  Общественное разделение труда и денежная система. Практическое занятие 4
Общественное разделение труда и денежная система. Практическое занятие 4 Последствия инфляции для различных социальных групп населения
Последствия инфляции для различных социальных групп населения Понятия, используемые в анализе систем, и проблемы их развития Подготовили: студенты 2 курса, Т-1202 Токманова Сандира Сембина Айга
Понятия, используемые в анализе систем, и проблемы их развития Подготовили: студенты 2 курса, Т-1202 Токманова Сандира Сембина Айга ВКР: Анализ экономической деятельности организации
ВКР: Анализ экономической деятельности организации Традиционная экономика
Традиционная экономика Программа содействия развитию постоянного гражданства Вануату
Программа содействия развитию постоянного гражданства Вануату Экономические системы, 8 класс
Экономические системы, 8 класс Финансы
Финансы Товарищество с Ограниченной Ответственностью КазМедФарма
Товарищество с Ограниченной Ответственностью КазМедФарма Время инвестиций прошло
Время инвестиций прошло Світовий ринок
Світовий ринок Общественные блага и принципы их классификации
Общественные блага и принципы их классификации Экономический анализ. (Модуль 2)
Экономический анализ. (Модуль 2) Получение нобелевских премий в отрасли Экономики
Получение нобелевских премий в отрасли Экономики Кадры организации и производительность труда
Кадры организации и производительность труда Суспільство ризику як суспільство споживання та наслідок кризи сучасної цивілізації
Суспільство ризику як суспільство споживання та наслідок кризи сучасної цивілізації Экономическая составляющая перехода Крыма в РФ
Экономическая составляющая перехода Крыма в РФ 3н61 Творческий проект. Школа инженерного предпринимательства
3н61 Творческий проект. Школа инженерного предпринимательства Рынок земли
Рынок земли Микроэкономика
Микроэкономика Классический этап экономической теории. Жан Батист Сэи
Классический этап экономической теории. Жан Батист Сэи Макроэкономика (2). Задания для выполнения
Макроэкономика (2). Задания для выполнения Economic overview of the project
Economic overview of the project Рынок и его функции
Рынок и его функции Типы производства и организация производственного процесса. (Тема 3)
Типы производства и организация производственного процесса. (Тема 3) Ограниченность ресурсов
Ограниченность ресурсов