2.Уравнение Бернулли. Давление жидкости на плоские и криволинейные поверхности

Коэффициент кинематической вязкости

Ньютоновские жидкости – жидкости,
которые полностью подчиняются закону Ньютона:
Напряжение сдвига не зависит от градиента скорости.
Вязкость – постоянная величина, оценивающаяся
коэффициентом вязкости
Неньтоновские жидкости – жидкости,
Которые не подчиняются закону Ньютона:
напряжение сдвига определяется
градиентом скорости.
Вязкость – величина переменная и зависит
от напряжения сдвига.

Гипотеза сплошности. Характеристики движения жидкости.
Уравнение Бернулли
Уравнение неразрывности для элементарной струйки несжимаемой жидкости:
Уравнение неразрывности:
Уравнение Бернулли для линии тока реальной жидкости:
При движении жидкости полная механическая энергия уменьшается
По длине элементарной струйки. Уравнение Бернулли для потока реальной жидкости

Геометрическая характеристика (диаграмма) уравнения Бернулли.

Линия Р-Р – пьезометрическая линия, характеризуется пьезометрическимуклоном

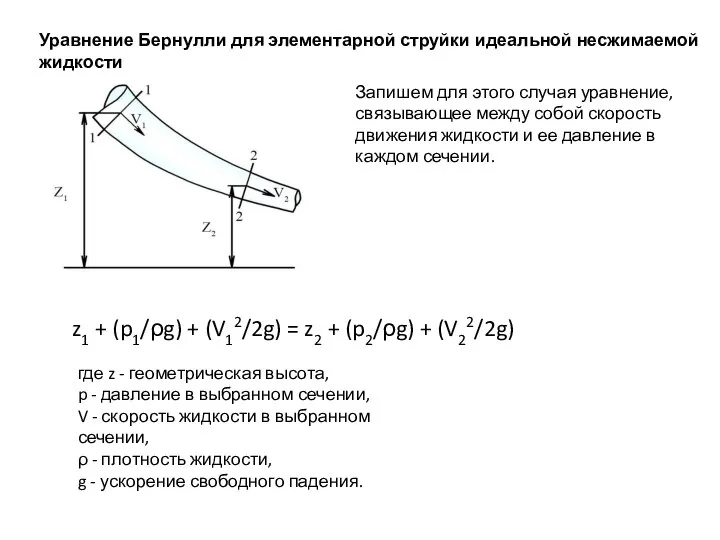
Уравнение Бернулли для элементарной струйки идеальной несжимаемой жидкости
Запишем для этого случая уравнение, связывающее между собой скорость движения жидкости и ее давление в каждом сечении.
z1 + (p1/ρg) + (V12/2g) = z2 + (p2/ρg) + (V22/2g)
где z - геометрическая высота,
p - давление в выбранном сечении,
V - скорость жидкости в выбранном сечении,
ρ - плотность жидкости,
g - ускорение свободного падения.

Для каждого рассматриваемого сечения полный напор есть сумма геометрического, пьезометрического и скоростного напора. Для идеальной жидкости (т.е. при отсутствии потерь энергии) полный напор - величина постоянная.
z + p/ρg + V2/2g = Н = const
где z - геометрический напор,
p/ρg - пьезометрический напор,
z + p/ρg - статический напор,
V2/2g - скоростной напор,
z + p/ρg + V2/2g = Н - полный напор.
Уравнение Бернулли можно записать и в другом виде, умножим обе части уравнения на g получим:
gz1 + p1/ρ + V12/2 = gz2 + p2/ρ + V22/2

Физический смысл уравнения Бернулли
Составляющие уравнения Бернулли являются различными формами удельной (отнесенной к единице массы) механической энергии жидкости:
gz - удельная энергия положения,
p/ρ - удельная энергия давления движущейся жидкости,
V12/2 - удельная кинетическая энергия жидкости,
gz + p/ρ + V2/2 = Hg - полная удельная энергия движущейся идеальной жидкости.
Физический и энергетический смысл уравнения Бернулли заключается в постоянстве полной удельной энергии вдоль элементарной струйки идеальной жидкости.

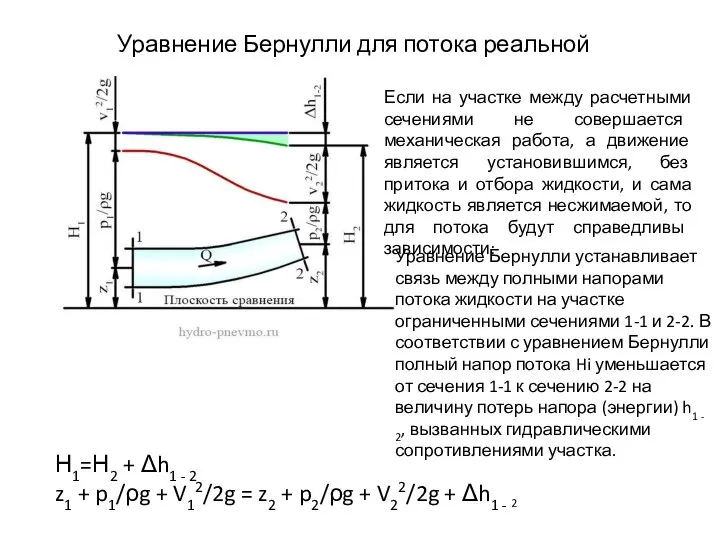
Уравнение Бернулли для потока реальной жидкости
Если на участке между расчетными сечениями не совершается механическая работа, а движение является установившимся, без притока и отбора жидкости, и сама жидкость является несжимаемой, то для потока будут справедливы зависимости:
Н1=Н2 + Δh1 - 2
z1 + p1/ρg + V12/2g = z2 + p2/ρg + V22/2g + Δh1 - 2
Уравнение Бернулли устанавливает связь между полными напорами потока жидкости на участке ограниченными сечениями 1-1 и 2-2. В соответствии с уравнением Бернулли полный напор потока Hi уменьшается от сечения 1-1 к сечению 2-2 на величину потерь напора (энергии) h1 - 2, вызванных гидравлическими сопротивлениями участка.

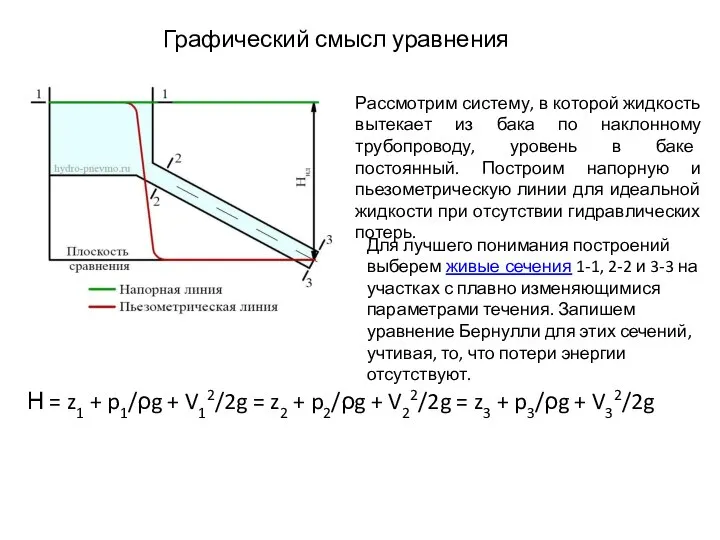
Графический смысл уравнения Бернулли
Рассмотрим систему, в которой жидкость вытекает из бака по наклонному трубопроводу, уровень в баке постоянный. Построим напорную и пьезометрическую линии для идеальной жидкости при отсутствии гидравлических потерь.
Для лучшего понимания построений выберем живые сечения 1-1, 2-2 и 3-3 на участках с плавно изменяющимися параметрами течения. Запишем уравнение Бернулли для этих сечений, учтивая, то, что потери энергии отсутствуют.
Н = z1 + p1/ρg + V12/2g = z2 + p2/ρg + V22/2g = z3 + p3/ρg + V32/2g

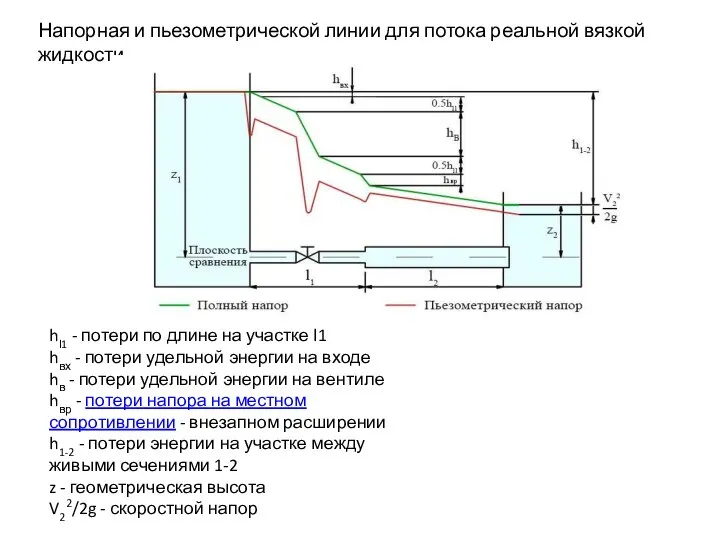
Напорная и пьезометрической линии для потока реальной вязкой жидкости
hl1 - потери по длине на участке l1
hвх - потери удельной энергии на входе
hв - потери удельной энергии на вентиле
hвр - потери напора на местном сопротивлении - внезапном расширении
h1-2 - потери энергии на участке между живыми сечениями 1-2
z - геометрическая высота
V22/2g - скоростной напор

Уравнение Бернулли для горизонтальной трубы
p1 + ρV12 = p2 + ρV22 + Δp1о

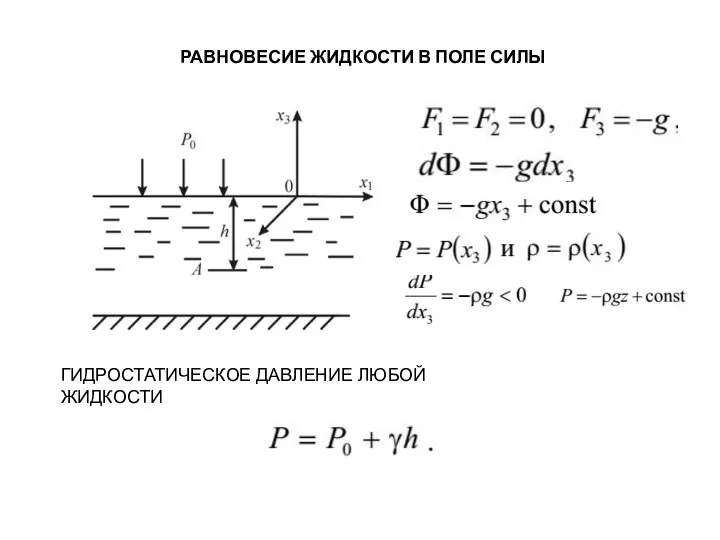
РАВНОВЕСИЕ ЖИДКОСТИ В ПОЛЕ СИЛЫ ТЯЖЕСТИ
ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ ЛЮБОЙ ЖИДКОСТИ

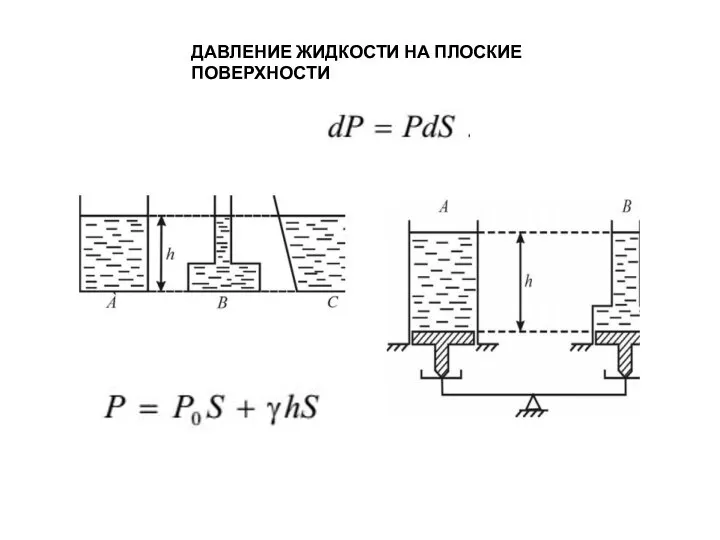
ДАВЛЕНИЕ ЖИДКОСТИ НА ПЛОСКИЕ ПОВЕРХНОСТИ

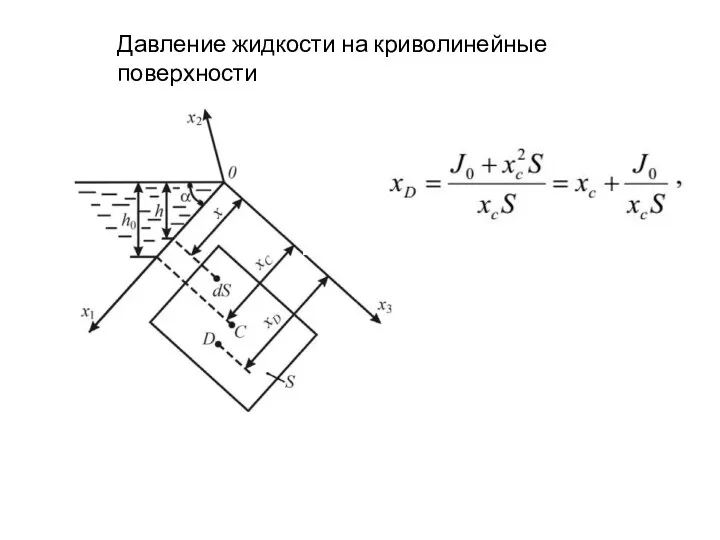
Давление жидкости на криволинейные поверхности

ЕСЛИ
ТО

Тело давления