Содержание
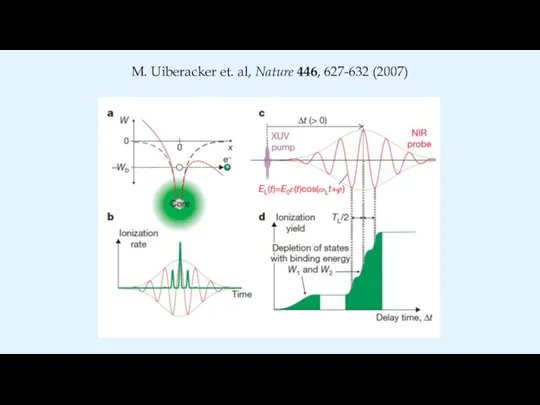
- 2. M. Uiberacker et. al, Nature 446, 627-632 (2007)
- 5. Туннельное время и неадиабатичность ионизации.
- 6. P. Eckle, A. Pfeiffer, C. Cirelli, A. Staudte, R. Dörner, H.-G. Muller, M. Büttiker, U. Keller,
- 7. Аттосекундные часы
- 8. Аттосекундные часы
- 9. Время Келдыша везде определяется как время, которое нужно электрону, имеющему скорость, определяющейся энергией его связанного состояния,
- 10. Туннельные времена Время Эйзенбада-Вигнера Время Поллака-Миллера Время Лармора Время Буттикера-Ландауэра
- 11. Неадиабатичность ионизации и туннельные времена Процесс туннелирования сопровождается противодействием атомного потенциала переходу электронов из связанных состояний
- 12. Временная задержка ионизации при туннелировании волнового пакета в переменном лазерном поле Время туннелирования (passage time), описывающее
- 13. Задержка ионизации при туннелировании волнового пакета в переменном лазерном поле Процесс туннелирования в высокоинтенсивном переменном лазерном
- 14. Физический смысл Фурье преобразования заключается в том, что производная фазы волнового пакета (по координате z) в
- 15. Полуклассическая модель формирования волнового пакета свободных электронов Фаза волнового пакета в импульсном представлении. С точки зрения
- 16. Если теперь в уравнении (7) мы учтём зависимость точки выхода от времени tb, в которое электрон
- 17. Из этого следует, что модуль амплитуды волнового пакета можно записать как квадратный корень из следующего выражения:
- 18. Импульсные спектры волновых пакетов свободных электронов |ψc(p)|2 в конце полуцикла поля, полученные в результате численного решения
- 19. Волновой пакет свободных электронов (показан розовым цветом) в конце полуцикла поля (пространственное представление реальной части волновой
- 20. Импульсные спектры волновых пакетов свободных электронов в конце полуцикла поля (T(ε)), рассчитанные при помощи полуклассической модели
- 21. Населённость континуума, рассчитанная в результате численного решения уравнения Шредингера (зелёная линия), а также в результате применения
- 22. Волновой пакет свободных электронов (показан розовым цветом) в конце полуцикла поля (пространственное представление реальной части волновой
- 23. Импульсные спектры волновых пакетов свободных электронов в конце полуцикла поля (T(ε)), рассчитанные при помощи полуклассической модели
- 24. Населённость континуума, рассчитанная в результате численного решения уравнения Шредингера (зелёная линия), а также в результате применения
- 25. Волновой пакет свободных электронов (показан розовым цветом) в конце полуцикла поля (пространственное представление реальной части волновой
- 26. Импульсные спектры волновых пакетов свободных электронов в конце полуцикла поля (T(ε)), рассчитанные при помощи полуклассической модели
- 27. Населённость континуума, рассчитанная в результате численного решения уравнения Шредингера (зелёная линия), а также в результате применения
- 28. Зависимость ширины стационарного барьера при пиковой интенсивности поля в сравнении с разницей средней координаты центра масс
- 29. и (c) – фазовое время, характеризующее фазовую задержку ионизации в результате наличия ненулевой точки выхода в
- 30. Время задержки профиля населённости континуума. Данное время было извлечено из пространственного представления волнового пакета, сформированного в
- 31. Сравнение дипольного момента внутри одиночного полуцикла, получаемого при помощи полуклассической модели и численного решения уравнения Шредингера
- 32. Сравнение дипольного момента внутри одиночного полуцикла, получаемого при помощи полуклассической модели и численного решения уравнения Шредингера
- 33. Сравнение дипольного момента внутри одиночного полуцикла, получаемого при помощи полуклассической модели и численного решения уравнения Шредингера
- 34. (а) – населённости континуума, полученные на основании численного решения уравнения Шредингера (синие линии), а также адиабатической
- 35. (с) – населённости континуума, полученные на основании численного решения уравнения Шредингера (синие линии), а также адиабатической
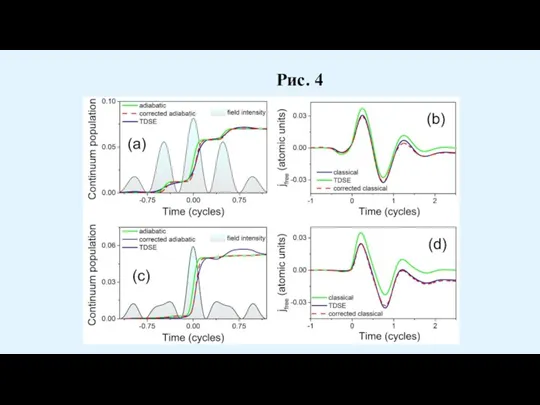
- 36. Рис. 4
- 37. Рассмотрим случай оптического нелинейного отклика атомарного водорода на действие двухчастотного поля, состоящего из основной частоты и
- 39. Скачать презентацию
Слайд 5Туннельное время и неадиабатичность ионизации.
Туннельное время и неадиабатичность ионизации.

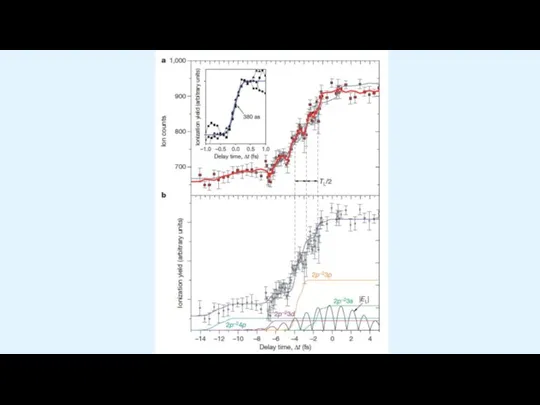
Слайд 6P. Eckle, A. Pfeiffer, C. Cirelli, A. Staudte, R. Dörner, H.-G. Muller,
P. Eckle, A. Pfeiffer, C. Cirelli, A. Staudte, R. Dörner, H.-G. Muller,

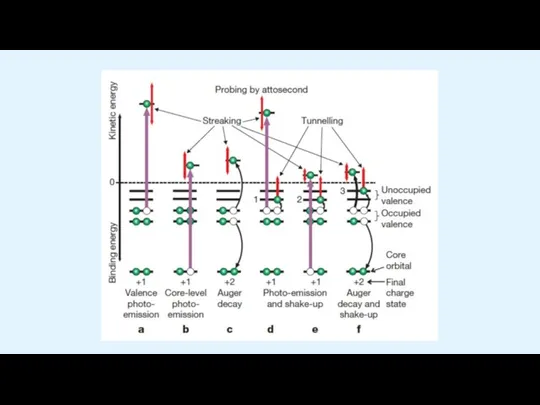
Аттосекундные часы
Слайд 7Аттосекундные часы
Аттосекундные часы
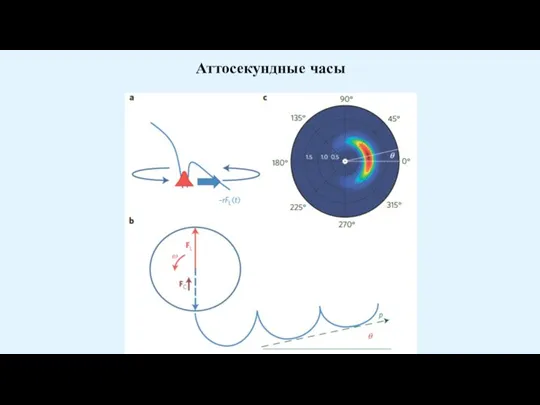
Слайд 8Аттосекундные часы
Аттосекундные часы
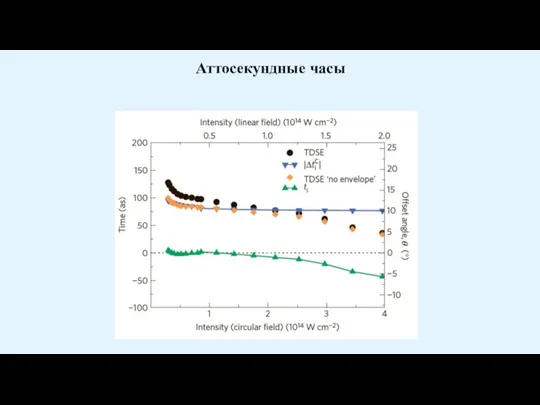
Слайд 9 Время Келдыша везде определяется как время, которое нужно электрону, имеющему скорость, определяющейся
Время Келдыша везде определяется как время, которое нужно электрону, имеющему скорость, определяющейся

Скорость электрона принимается равной:
В этом случае время Келдыша будет иметь вид:
С учётом того, что параметр Келдыша равен:
Время туннелирования по Келдышу принимает следующее значение:
Время туннелирования Келдыша
Слайд 10Туннельные времена
Время Эйзенбада-Вигнера
Время Поллака-Миллера
Время Лармора
Время Буттикера-Ландауэра
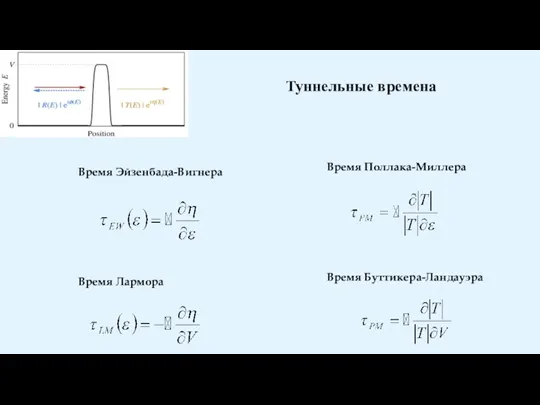
Туннельные времена
Время Эйзенбада-Вигнера
Время Поллака-Миллера
Время Лармора
Время Буттикера-Ландауэра
Слайд 11Неадиабатичность ионизации и туннельные времена
Процесс туннелирования сопровождается противодействием атомного потенциала переходу электронов
Неадиабатичность ионизации и туннельные времена
Процесс туннелирования сопровождается противодействием атомного потенциала переходу электронов

Существуют четыре основных выражения для времён туннелирования (Buttiker-Landauer time, Larmor time, Eisenbud–Wigner и Pollac-Miller time), записанных в терминах прошедшего (туннелировавшего через барьер) электронного волнового пакета. В обзорной статье Урсулы Келлер показано [Ursula Keller 2014 J. Phys. B: At. Mol. Opt. Phys], что эти времена могут быть попарно объединены в рамках формализма интегралов Феймана. Первая пара времён (Buttiker-Landauer time и Larmor time) является действительной и мнимой частью среднего времени, которое частица проводит под барьером (нужно усреднить время, которое частица с некоторой энергией проводит под барьером). Эти времена можно назвать временами жизни частицы под барьером (resident or dwell time). Альтернативное определение времени жизни частицы под барьером приводит к так называемому времени прохода под барьером passage time (усреднение времени, определяющегося как разница между моментом выхода из под барьера и моментом входа под барьер). В этом случае время туннелирования представляется в виде комплексного выражения, в котором действительная часть представляет из себя время Эйзенбада-Вигнера, а мнимая часть соответствует времени Поллака-Миллера.
Слайд 12Временная задержка ионизации при туннелировании волнового пакета в переменном лазерном поле
Время туннелирования
Временная задержка ионизации при туннелировании волнового пакета в переменном лазерном поле
Время туннелирования
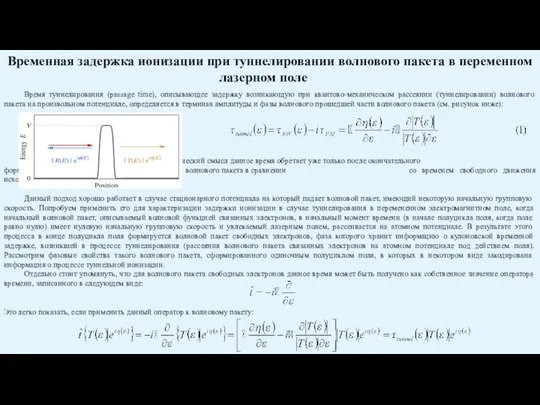
Причём физический смысл данное время обретает уже только после окончательного формирования исходящего (туннелировавшей части) волнового пакета в сравнении со временем свободного движения исходного волнового пакета.
Данный подход хорошо работает в случае стационарного потенциала на который падает волновой пакет, имеющий некоторую начальную групповую скорость. Попробуем применить его для характеризации задержки ионизации в случае туннелирования в перемененном электромагнитном поле, когда начальный волновой пакет, описываемый волновой функцией связанных электронов, в начальный момент времени (в начале полуцикла поля, когда поле равно нулю) имеет нулевую начальную групповую скорость и увлекаемый лазерным полем, рассеивается на атомном потенциале. В результате этого процесса в конце полуцикла поля формируется волновой пакет свободных электронов, фаза которого хранит информацию о кулоновской временной задержке, возникшей в процессе туннелирования (рассеяния волнового пакета связанных электронов на атомном потенциале под действием поля). Рассмотрим фазовые свойства такого волнового пакета, сформированного одиночным полуциклом поля, в которых в некотором виде закодирована информация о процессе туннельной ионизации.
Отдельно стоит упомянуть, что для волнового пакета свободных электронов данное время может быть получено как собственное значение оператора времени, записанного в следующем виде:
Это легко показать, если применить данный оператор к волновому пакету:
Слайд 13 Задержка ионизации при туннелировании волнового пакета в переменном лазерном поле
Процесс туннелирования
Задержка ионизации при туннелировании волнового пакета в переменном лазерном поле
Процесс туннелирования

TDSE
В случае численного анализа нестационарного уравнения Шредингера для одиночного атома водорода волновой пакет свободных электронов в конце полуцикла поля получался в результате вычитания из полной волновой функции волнового пакета связанных электронов. Полученная часть волновой функции, зависящей от поперечной координаты и координаты z, направленной вдоль направления поляризации поля, использовалась для получения импульсного спектра волнового пакета свободных электронов. Характерные импульсные распределения волновых пакетов в конце полуцикла поля для атома водорода показаны на последнем слайде данной презентации. Для упрощения анализа было произведено интегрирование по поперечной координате, что позволило рассматривать зависимость характеристик волнового пакета только от координаты z:
Импульсный спектр полученного одномерного волнового пакета находился благодаря Фурье преобразованию:
Слайд 14 Физический смысл Фурье преобразования заключается в том, что производная фазы волнового пакета
Физический смысл Фурье преобразования заключается в том, что производная фазы волнового пакета

Фазовое время находится из импульсного распределения волнового пакета дифференцирования его фазы по энергии:
Это фазовое время, как видно из формулы (3), равно отношению координаты электрона, которую он имеет в конце полуцикла к набранной им скорости:
Так как можно считать, что электроны в момент своего рождения в континууме имеют нулевую начальную скорость, то в нашем случае vz – это скорость, которую электрон набрал за время своего свободного распространения в лазерном поле (с момента рождения до конца полуцикла поля, а z(ε) –это координата электрона, в которую попадает электрон в конце полуцикла поля с энергией ε.
Квадрат амплитуды волнового пакета в зависимости от энергии электронов в соответствии с (1) имеет следующий вид:
Полученные свойства волновых пакетов в результате численного моделирования нестационарного уравнения Шредингера сравним с результатом полуклассической модели, описание которой приведено на следующих слайдах.
Слайд 15Полуклассическая модель формирования волнового пакета свободных электронов
Фаза волнового пакета в импульсном представлении.
С
Полуклассическая модель формирования волнового пакета свободных электронов
Фаза волнового пакета в импульсном представлении.
С

Расстояние, которое электрон пролетает за это время (от tb до π/ω), будет равняться следующему значению:
Формула (6) задаёт обратную зависимость энергии электрона от момент в который он перешёл в континуум:
Используя которую, в формуле (7) мы получаем зависимость координаты электрона в конце полуцикла от его энергии
Как показывает сравнение численного решения уравнения Шредингера (см. формулу (3)) с полуклассической моделью (формула (8)), удаление электронов от начала координат в квантово-механическом случае оказывается большим по сравнении с полуклассической моделью (см. слайды 6, 9, 12). Усреднение этой разницы по ансамблю электронов в полном соответствии с теорией туннелирования Келдыша даёт нам величину очень близкую к ширине потенциального барьера (см. слайд 15), который получается при пиковой интенсивности поля (в центре полуцикла):
Слайд 16Если теперь в уравнении (7) мы учтём зависимость точки выхода от времени
Если теперь в уравнении (7) мы учтём зависимость точки выхода от времени

Формула (10) совместно с формулой (6) определяют производную фазы волнового пакета свободных электронов, которая получается при учёте не нулевой точки выхода электронов в континуум, которая равна мгновенной ширине барьера (в момент перехода электрона в свободное состояние).
Амплитуда волнового пакета в импульсном представлении.
В отличии от фазы, амплитуда волнового пакета в импульсном представлении вообще не зависит от того, в какой точке электрон перешёл в континуум. Для амплитуды важно только сколько именно электронов стало свободными в каждый конкретный момент времени (чем раньше в пределах полуцикла электрон стал свободным, тем больше у него будет энергия). Это значит, что амплитуда волнового пакета континуума однозначным образом определяется профилем населённости континуума C(tb) (точнее скоростью ионизации, которая является производной от C(tb)) и параметрами цикла лазерного поля. Для вычисления скорости ионизации и населённости континуума в рамках полуклассической модели была использована адиабатическая модель ионизации (см. предпоследний слайд).
Квадрат амплитуды волнового пакета свободных электронов (волновой функции) в зависимости от энергии T(ε) -- это функция плотности вероятности. Связать её с профилем населённости континуума можно с помощью следующего простого соображения. Так как мы рассматриваем зависимость волновой функции от энергии, то количество электронов вылетевших в континуум за интервал времени dtb, окажется распределёнными по энергии в окрестности точки ε = f(tb) (которая через скорость является однозначной функцией времени tb) на интервале dε, определяющемся производной этой функции:
Количество электронов в на этом интервале по определению функции плотности вероятности будет равно:
а с другой стороны это количество электронов равно приращению населённости континуума в момент времени tb за интервал времени dtb, что позволяет связать амплитуду волновой функции свободных электронов в конце полуцикла со скоростью изменения населённости континуума внутри полуцикла:
Слайд 17Из этого следует, что модуль амплитуды волнового пакета можно записать как квадратный
Из этого следует, что модуль амплитуды волнового пакета можно записать как квадратный

Фазовое время в полуклассической модели.
Для нахождения фазового времени в полуклассической модели перепишем формулу (5) с учётом известных нам скорости и координаты электронов в конце полуцикла:
Если использовать для координаты формулу (10), которая учитывает ненулевую точку выхода, то мы получим следующее выражение:
Формулы (12) и (13) были использованы для построения фазовых времён на слайдах 7, 10 и 13.
Слайд 18Импульсные спектры волновых пакетов свободных электронов |ψc(p)|2 в конце полуцикла поля, полученные
Импульсные спектры волновых пакетов свободных электронов |ψc(p)|2 в конце полуцикла поля, полученные
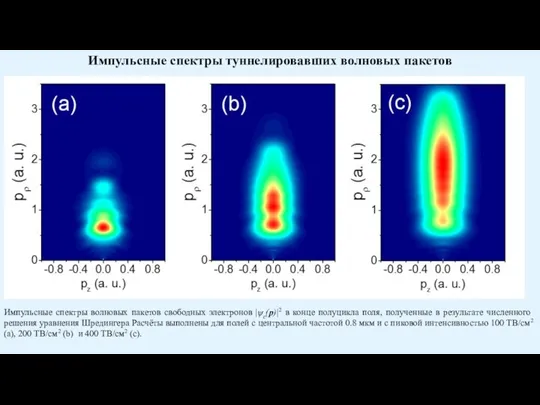
Импульсные спектры туннелировавших волновых пакетов
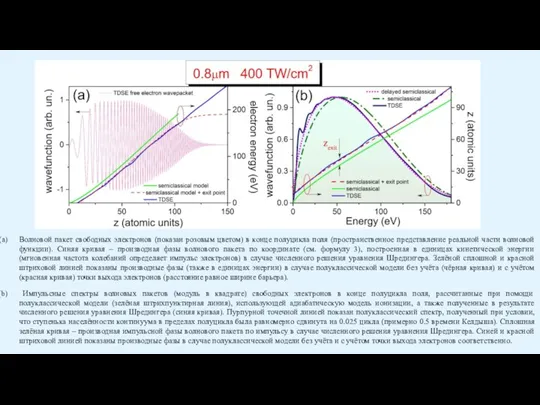
Слайд 19Волновой пакет свободных электронов (показан розовым цветом) в конце полуцикла поля (пространственное
Волновой пакет свободных электронов (показан розовым цветом) в конце полуцикла поля (пространственное
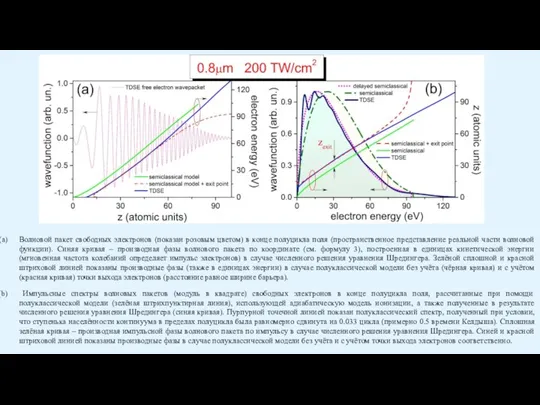
Импульсные спектры волновых пакетов (модуль в квадрате) свободных электронов в конце полуцикла поля, рассчитанные при помощи полуклассической модели (зелёная штрихпунктирная линия), использующей адиабатическую модель ионизации, а также полученные в результате численного решения уравнения Шредингера (синяя кривая). Пурпурной точечной линией показан полуклассический спектр, полученный при условии, что ступенька населённости континуума в пределах полуцикла была равномерно сдвинута на 0.033 цикла (примерно 0.5 времени Келдыша). Сплошная зелёная кривая – производная импульсной фазы волнового пакета по импульсу в случае численного решения уравнения Шредингера. Синей и красной штриховой линией показаны производные фазы в случае полуклассической модели без учёта и с учётом точки выхода электронов соответственно.
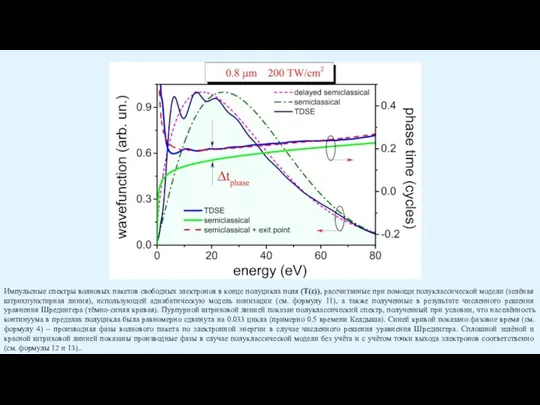
Слайд 20Импульсные спектры волновых пакетов свободных электронов в конце полуцикла поля (T(ε)), рассчитанные
Импульсные спектры волновых пакетов свободных электронов в конце полуцикла поля (T(ε)), рассчитанные
Слайд 21Населённость континуума, рассчитанная в результате численного решения уравнения Шредингера (зелёная линия), а
Населённость континуума, рассчитанная в результате численного решения уравнения Шредингера (зелёная линия), а
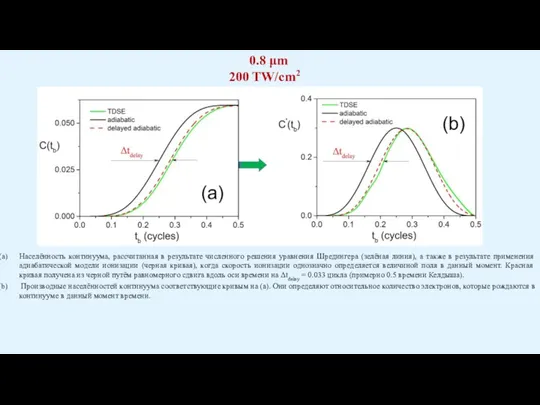
Производные населённостей континуума соответствующие кривым на (а). Они определяют относительное количество электронов, которые рождаются в континууме в данный момент времени.
0.8 μm
200 TW/cm2
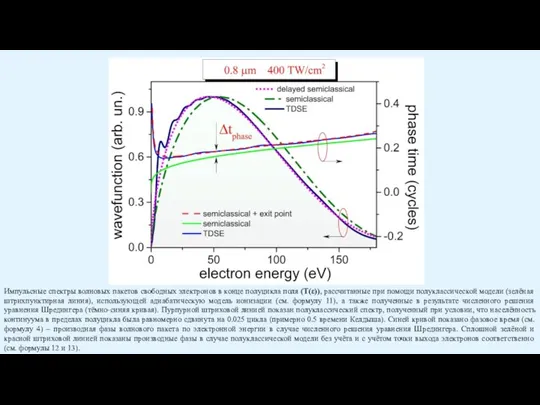
Слайд 22Волновой пакет свободных электронов (показан розовым цветом) в конце полуцикла поля (пространственное
Волновой пакет свободных электронов (показан розовым цветом) в конце полуцикла поля (пространственное
Импульсные спектры волновых пакетов (модуль в квадрате) свободных электронов в конце полуцикла поля, рассчитанные при помощи полуклассической модели (зелёная штрихпунктирная линия), использующей адиабатическую модель ионизации, а также полученные в результате численного решения уравнения Шредингера (синяя кривая). Пурпурной точечной линией показан полуклассический спектр, полученный при условии, что ступенька населённости континуума в пределах полуцикла была равномерно сдвинута на 0.025 цикла (примерно 0.5 времени Келдыша). Сплошная зелёная кривая – производная импульсной фазы волнового пакета по импульсу в случае численного решения уравнения Шредингера. Синей и красной штриховой линией показаны производные фазы в случае полуклассической модели без учёта и с учётом точки выхода электронов соответственно.
Слайд 23Импульсные спектры волновых пакетов свободных электронов в конце полуцикла поля (T(ε)), рассчитанные
Импульсные спектры волновых пакетов свободных электронов в конце полуцикла поля (T(ε)), рассчитанные
Слайд 24Населённость континуума, рассчитанная в результате численного решения уравнения Шредингера (зелёная линия), а
Населённость континуума, рассчитанная в результате численного решения уравнения Шредингера (зелёная линия), а
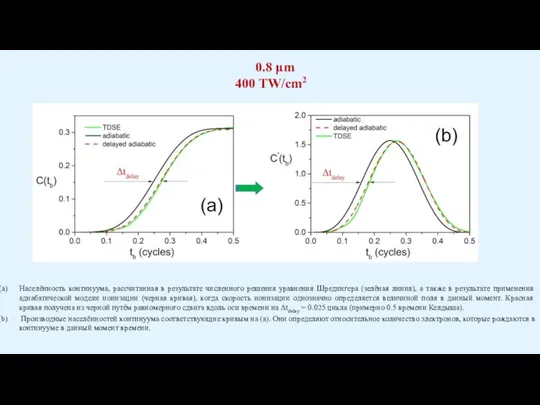
Производные населённостей континуума соответствующие кривым на (а). Они определяют относительное количество электронов, которые рождаются в континууме в данный момент времени.
0.8 μm
400 TW/cm2
Слайд 25Волновой пакет свободных электронов (показан розовым цветом) в конце полуцикла поля (пространственное
Волновой пакет свободных электронов (показан розовым цветом) в конце полуцикла поля (пространственное
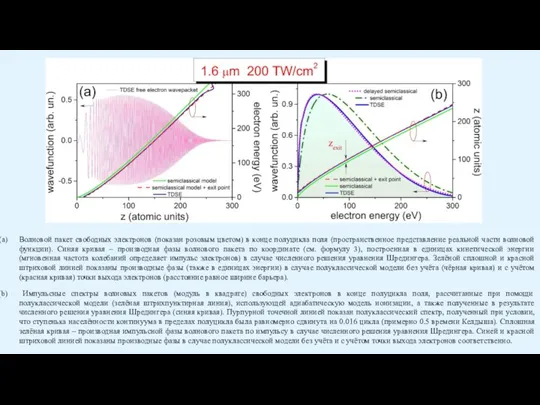
Импульсные спектры волновых пакетов (модуль в квадрате) свободных электронов в конце полуцикла поля, рассчитанные при помощи полуклассической модели (зелёная штрихпунктирная линия), использующей адиабатическую модель ионизации, а также полученные в результате численного решения уравнения Шредингера (синяя кривая). Пурпурной точечной линией показан полуклассический спектр, полученный при условии, что ступенька населённости континуума в пределах полуцикла была равномерно сдвинута на 0.016 цикла (примерно 0.5 времени Келдыша). Сплошная зелёная кривая – производная импульсной фазы волнового пакета по импульсу в случае численного решения уравнения Шредингера. Синей и красной штриховой линией показаны производные фазы в случае полуклассической модели без учёта и с учётом точки выхода электронов соответственно.
Слайд 26Импульсные спектры волновых пакетов свободных электронов в конце полуцикла поля (T(ε)), рассчитанные
Импульсные спектры волновых пакетов свободных электронов в конце полуцикла поля (T(ε)), рассчитанные
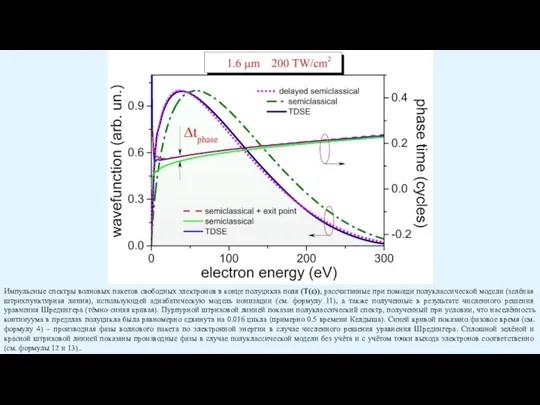
Слайд 27Населённость континуума, рассчитанная в результате численного решения уравнения Шредингера (зелёная линия), а
Населённость континуума, рассчитанная в результате численного решения уравнения Шредингера (зелёная линия), а
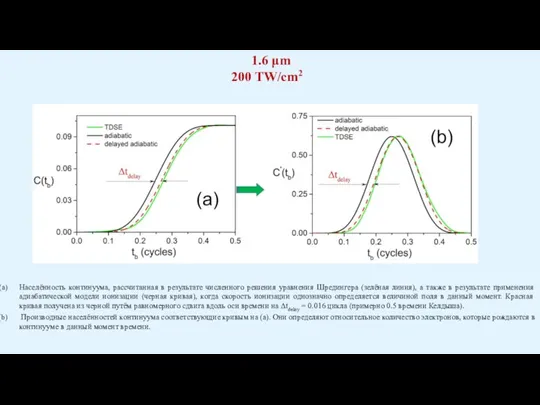
Производные населённостей континуума соответствующие кривым на (а). Они определяют относительное количество электронов, которые рождаются в континууме в данный момент времени.
1.6 μm
200 TW/cm2
Слайд 28Зависимость ширины стационарного барьера при пиковой интенсивности поля в сравнении с разницей
Зависимость ширины стационарного барьера при пиковой интенсивности поля в сравнении с разницей
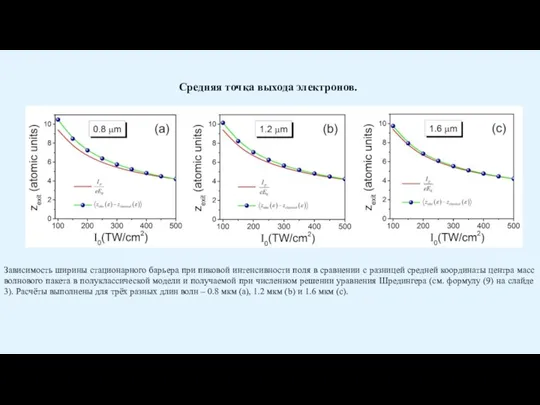
Средняя точка выхода электронов.
Слайд 29и (c) – фазовое время, характеризующее фазовую задержку ионизации в результате наличия
и (c) – фазовое время, характеризующее фазовую задержку ионизации в результате наличия
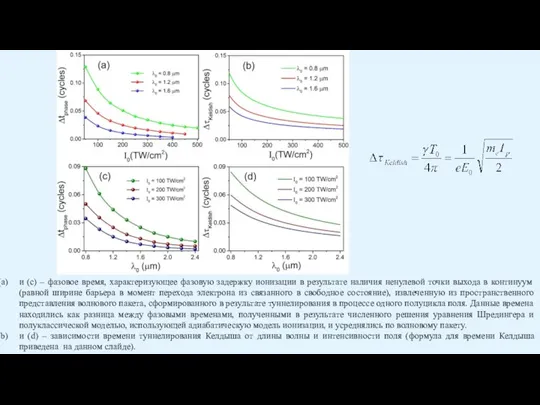
и (d) – зависимости времени туннелирования Келдыша от длины волны и интенсивности поля (формула для времени Келдыша приведена на данном слайде).
Слайд 30Время задержки профиля населённости континуума. Данное время было извлечено из пространственного представления
Время задержки профиля населённости континуума. Данное время было извлечено из пространственного представления
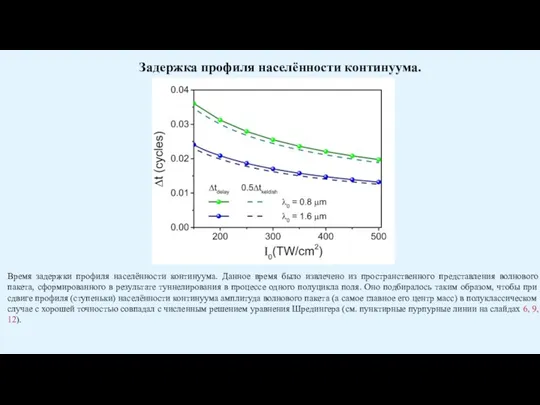
Задержка профиля населённости континуума.
Слайд 31Сравнение дипольного момента внутри одиночного полуцикла, получаемого при помощи полуклассической модели
и
Сравнение дипольного момента внутри одиночного полуцикла, получаемого при помощи полуклассической модели
и
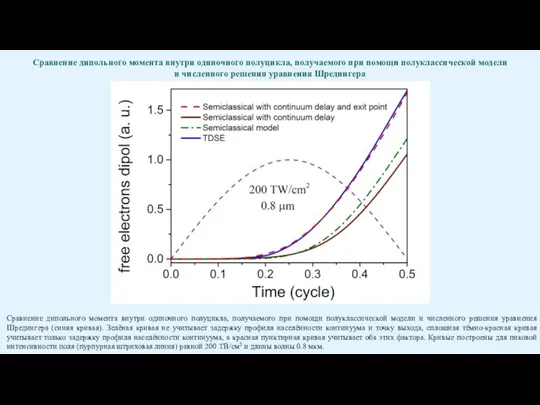
Сравнение дипольного момента внутри одиночного полуцикла, получаемого при помощи полуклассической модели и численного решения уравнения Шредингера (синяя кривая). Зелёная кривая не учитывает задержку профиля населённости континуума и точку выхода, сплошная тёмно-красная кривая учитывает только задержку профиля населённости континуума, а красная пунктирная кривая учитывает оба этих фактора. Кривые построены для пиковой интенсивности поля (пурпурная штриховая линия) равной 200 ТВ/см2 и длины волны 0.8 мкм.
Слайд 32Сравнение дипольного момента внутри одиночного полуцикла, получаемого при помощи полуклассической модели
и
Сравнение дипольного момента внутри одиночного полуцикла, получаемого при помощи полуклассической модели
и
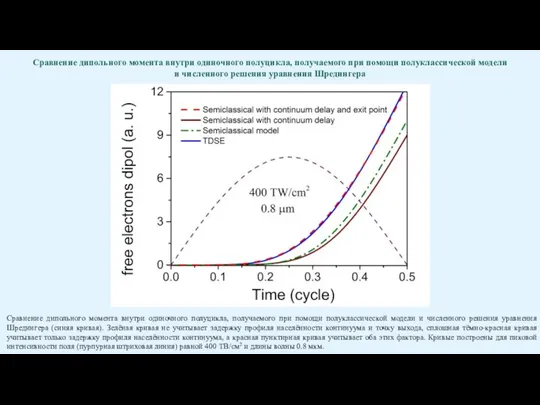
Сравнение дипольного момента внутри одиночного полуцикла, получаемого при помощи полуклассической модели и численного решения уравнения Шредингера (синяя кривая). Зелёная кривая не учитывает задержку профиля населённости континуума и точку выхода, сплошная тёмно-красная кривая учитывает только задержку профиля населённости континуума, а красная пунктирная кривая учитывает оба этих фактора. Кривые построены для пиковой интенсивности поля (пурпурная штриховая линия) равной 400 ТВ/см2 и длины волны 0.8 мкм.
Слайд 33Сравнение дипольного момента внутри одиночного полуцикла, получаемого при помощи полуклассической модели
и
Сравнение дипольного момента внутри одиночного полуцикла, получаемого при помощи полуклассической модели
и
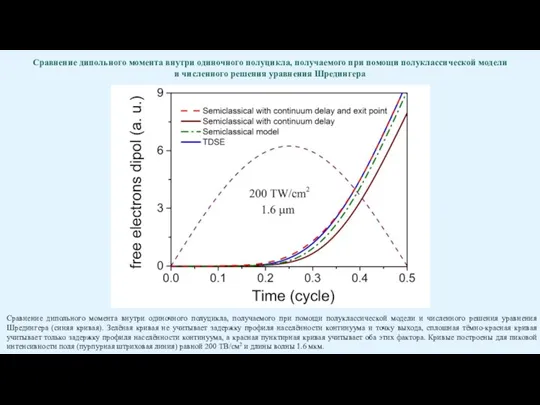
Сравнение дипольного момента внутри одиночного полуцикла, получаемого при помощи полуклассической модели и численного решения уравнения Шредингера (синяя кривая). Зелёная кривая не учитывает задержку профиля населённости континуума и точку выхода, сплошная тёмно-красная кривая учитывает только задержку профиля населённости континуума, а красная пунктирная кривая учитывает оба этих фактора. Кривые построены для пиковой интенсивности поля (пурпурная штриховая линия) равной 200 ТВ/см2 и длины волны 1.6 мкм.
Слайд 34(а) – населённости континуума, полученные на основании численного решения уравнения Шредингера (синие
(а) – населённости континуума, полученные на основании численного решения уравнения Шредингера (синие
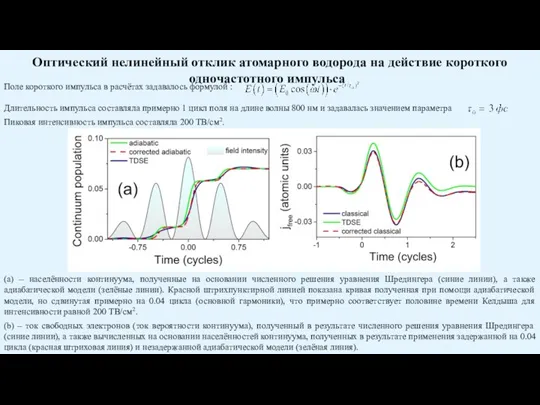
(b) – ток свободных электронов (ток вероятности континуума), полученный в результате численного решения уравнения Шредингера (синие линии), а также вычисленных на основании населённостей континуума, полученных в результате применения задержанной на 0.04 цикла (красная штриховая линия) и незадержанной адиабатической модели (зелёная линия).
Поле короткого импульса в расчётах задавалось формулой :
Длительность импульса составляла примерно 1 цикл поля на длине волны 800 нм и задавалась значением параметра
Пиковая интенсивность импульса составляла 200 ТВ/см2.
Оптический нелинейный отклик атомарного водорода на действие короткого одночастотного импульса
Слайд 35(с) – населённости континуума, полученные на основании численного решения уравнения Шредингера (синие
(с) – населённости континуума, полученные на основании численного решения уравнения Шредингера (синие
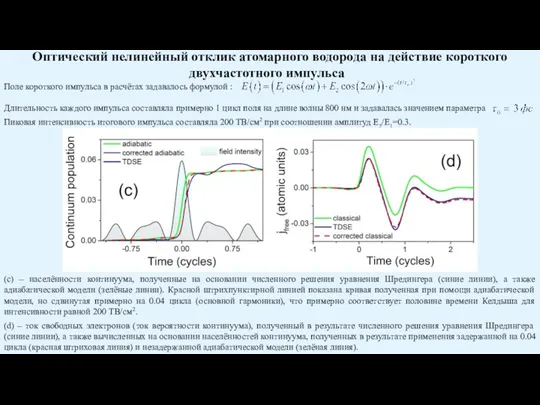
(d) – ток свободных электронов (ток вероятности континуума), полученный в результате численного решения уравнения Шредингера (синие линии), а также вычисленных на основании населённостей континуума, полученных в результате применения задержанной на 0.04 цикла (красная штриховая линия) и незадержанной адиабатической модели (зелёная линия).
Поле короткого импульса в расчётах задавалось формулой :
Длительность каждого импульса составляла примерно 1 цикл поля на длине волны 800 нм и задавалась значением параметра
Пиковая интенсивность итогового импульса составляла 200 ТВ/см2 при соотношении амплитуд Е2/Е1=0.3.
Оптический нелинейный отклик атомарного водорода на действие короткого двухчастотного импульса
Слайд 36Рис. 4
Слайд 37Рассмотрим случай оптического нелинейного отклика атомарного водорода на действие двухчастотного поля, состоящего

Импульс в расчётах задавался формулой :
В расчётах, представленных на следующем слайде, соотношение амплитуд первой и второй гармоник всегда было одинаковым:
Длительность импульса основной и второй гармоник в расчётах была одинаковой и задавалась значением параметра
Несущие импульсов с разной фазовой расстройкой между гармониками, а также их спектр (не зависит от расстройки), показаны на графиках (а) и (b) соответственно (см. следующий слайд). Населённость континуума, полученная при помощи численного решения уравнения Шредингера показана синей линией на панелях (с) и (е). Результат, который получается на основании адиабатической модели представлена на этих графиках зелёной линией, а красной штрихпунктирной линией показана эта же кривая, но сдвинутая примерно на 0.04 цикла (основной гармоники), что примерно соответствует половине времени Келдыша для интенсивности равной 200 ТВ/см2.
На панелях (d) и (f) показан ток свободных электронов. Синей кривой показан результат численного решения уравнения Шредингера, а красной штриховой и сплошной зелёной линиями представлены зависимости полуклассического тока свободных электронов, вычисленных на основании населённостей континуума, полученных в результате применения задержанной (на 0.04 цикла) и незадержанной адиабатической модели.
Оптический нелинейный отклик атомарного водорода на действие короткого двухчастотного импульса
 Механика. Гравитационные силы. Силы инерции
Механика. Гравитационные силы. Силы инерции Презентация на тему Механические свойства твердых тел
Презентация на тему Механические свойства твердых тел  Опыт Милликена. АФ1.4
Опыт Милликена. АФ1.4 Электроемкость.Конденсаторы
Электроемкость.Конденсаторы Презентация на тему Влияние радиоактивного излучения на живые организмы
Презентация на тему Влияние радиоактивного излучения на живые организмы  Использование электромагнитной индукции
Использование электромагнитной индукции Управление электродвигателем в заданной последовательности
Управление электродвигателем в заданной последовательности Розкладання білого світла на кольори. Утворення кольорів
Розкладання білого світла на кольори. Утворення кольорів Презентация на тему Постоянные магниты Магнитное поле Земли
Презентация на тему Постоянные магниты Магнитное поле Земли  Презентация на тему Давление света
Презентация на тему Давление света  Расчет некоторых оптических систем по теории аберраций третьих порядков
Расчет некоторых оптических систем по теории аберраций третьих порядков АМ БМ ОМ - математические модели сигналов. Тест
АМ БМ ОМ - математические модели сигналов. Тест Действие магнитного поля на проводник с током и движущийся заряд
Действие магнитного поля на проводник с током и движущийся заряд Сравнительная характеристика проводниковых материалов. Медь и алюминий
Сравнительная характеристика проводниковых материалов. Медь и алюминий Двигатель внутреннего сгорания
Двигатель внутреннего сгорания Оптические явления во сне и наяву
Оптические явления во сне и наяву Разряд вдоль поверхности твердого диэлектрика. Лекция 4
Разряд вдоль поверхности твердого диэлектрика. Лекция 4 Динамика. Инерциальные системы отсчета. Законы Ньютона
Динамика. Инерциальные системы отсчета. Законы Ньютона Фотоэффект
Фотоэффект Преобразование диаграммы условного напряжения - деформация в диаграмму истинного напряжения - деформация в программе Abaqus
Преобразование диаграммы условного напряжения - деформация в диаграмму истинного напряжения - деформация в программе Abaqus Динамическая метеорология. Термический ветер
Динамическая метеорология. Термический ветер Магнитное взаимодействие. Искусственные и естественные магниты
Магнитное взаимодействие. Искусственные и естественные магниты Устройство карданной передачи, разработка технологической карты
Устройство карданной передачи, разработка технологической карты Лазерные технологии
Лазерные технологии Водяная ракета
Водяная ракета Разработка привода руля направления транспортного самолета
Разработка привода руля направления транспортного самолета Поле чудес для знатоков физики
Поле чудес для знатоков физики Сила тяжести
Сила тяжести