Примеры решения задач по теме Кинематика твёрдого тела

Рекомендации:
При решении задач по этой теме обращайте внимание на связь кинематических характеристик поступательного и вращательного движений. При этом могут быть в одних случаях одинаковыми угловые скорости (например, задача 2), а в других — линейные скорости движения (например, задача 1).

Задача 1.
Два шкива соединены ременной передачей, передающей вращение от одного шкива к другому. Ведущий шкив вращается с частотой ν1 = 3000 об/мин, ведомый шкив — с частотой ν2 = 600 об/мин. Ведомый шкив имеет диаметр D2 = 500 мм. Какой диаметр D1 у ведущего шкива?
Р е ш е н и е. Ведущий шкив вращается с угловой скоростью ω1 = 2πν1, а ведомый — со скоростью ω2 = 2πν2. Скорость приводного ремня равна линейной скорости точек окружностей того и другого шкива: υ = ω1R1 = ω2R2.
Отсюда
Следовательно, искомый диаметр
.

Задача 2
Колесо, радиус которого 40 см, катится по
горизонтальной дороге со скоростью 2 м/с.
Определите скорости относительно дороги
точек колеса, находящихся на концах его
вертикального и горизонтального диаметров,
а также ускорения этих точек.
Р е ш е н и е. Точка О1 неподвижна относительно земли, следовательно, υ1=0. Если считать, что через точку О1 проходит мгновенная ось вращения, то относительно неё скорости всех точек, согласно уравнению (1.29), будут равны υ=ωr, где r — расстояние от точки O1 до выбранной точки обода. Угловая скорость вращения ω=υ0/R.
Тогда υc = υD = ωR√2 = υ0√2 ≈ 2,8 м/с.
Скорость точки A υA = 2ωR = 2υ0 = 4 м/с.
Все точки обода относительно оси вращения движутся с одинаковыми линейными скоростями и, следовательно, с одинаковым ускорениями
Заметим, что эту задачу также можно решить на основе закона сложения скоростей. Так, например, скорость точки D равна сумме скорости υ0 подвижной системы отсчёта, связанной с осью колеса, и скорости υ1 точки обода D относительно этой оси.

Задача 3
Катушка с намотанной на неё нитью может катиться по поверхности горизонтального стола без скольжения. С какой скоростью υ0 и в каком направлении будет перемещаться ось катушки, если конец нити тянуть в горизонтальном направлении со скоростью υ? Радиус внутренней части катушки r, внешней — R
Р е ш е н и е. Скорость υ — скорость движения нити — совпадает со скоростью точки А внутренней части катушки. Омгн — мгновенная ось вращения.
Угловая скорость относительно мгновенной оси вращения ω = υ/(R - r), так как расстояние
ОмгнА = R - r. Отсюда υ0 = ωR = υR/(R - r).
Очевидно, что катушка перемещается в направлении движения конца нити. Скорость перемещения катушки будет больше, чем скорость нити.

Задача 4
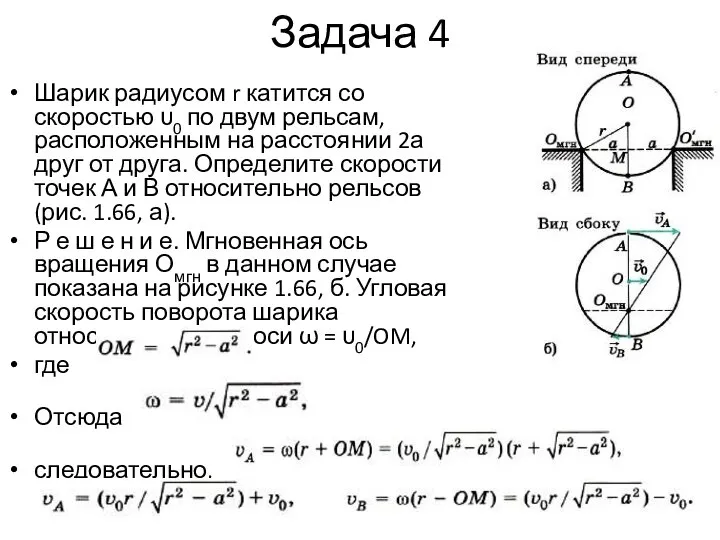
Шарик радиусом r катится со скоростью υ0 по двум рельсам, расположенным на расстоянии 2а друг от друга. Определите скорости точек А и В относительно рельсов (рис. 1.66, а).
Р е ш е н и е. Мгновенная ось вращения Омгн в данном случае показана на рисунке 1.66, б. Угловая скорость поворота шарика относительно этой оси ω = υ0/OM,
где
Отсюда
следовательно,

Домашнее задание:
§ 17
Задачи для самостоятельного решения (стр. 63)
ТЕСТ «Кинематика твёрдого тела»