Содержание
- 2. Тема № 3 «ДИНАМИКА КРИСТАЛЛИЧЕСКОЙ РЕШЁТКИ» 1.Квантование колебаний кристаллической решетки. Метод квазичастиц. Фононы. 2. Затруднения классической
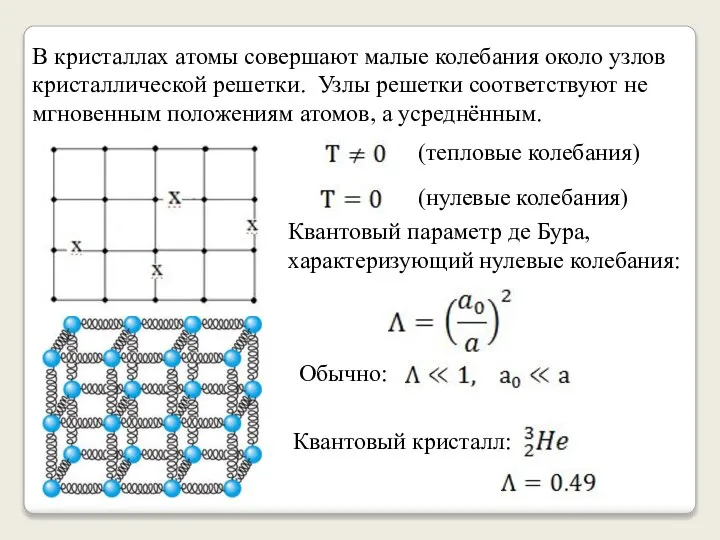
- 3. В кристаллах атомы совершают малые колебания около узлов кристаллической решетки. Узлы решетки соответствуют не мгновенным положениям
- 4. 1.Квантование колебаний кристаллической решетки. Метод квазичастиц. Фононы. В классической механике малые колебания системы со многими степенями
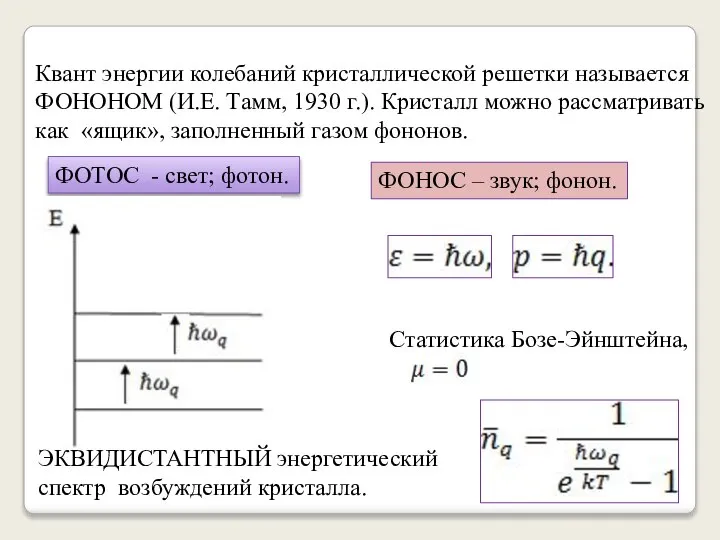
- 5. Квант энергии колебаний кристаллической решетки называется ФОНОНОМ (И.Е. Тамм, 1930 г.). Кристалл можно рассматривать как «ящик»,
- 6. Метод квазичастиц для описания систем из большого числа частиц. Сформулирован Л.Д.Ландау в 1941 г. при создании
- 7. Элементарные возбуждения (квазичастицы) в твердых телах: Фонон – квант энергии колебаний кристаллической решетки. Экситон – электронное
- 8. 2. Затруднения классической теории теплоёмкости кристаллов. Кристалл рассматривается как совокупность N независимых гармонических осцилляторов, имеющих 3N
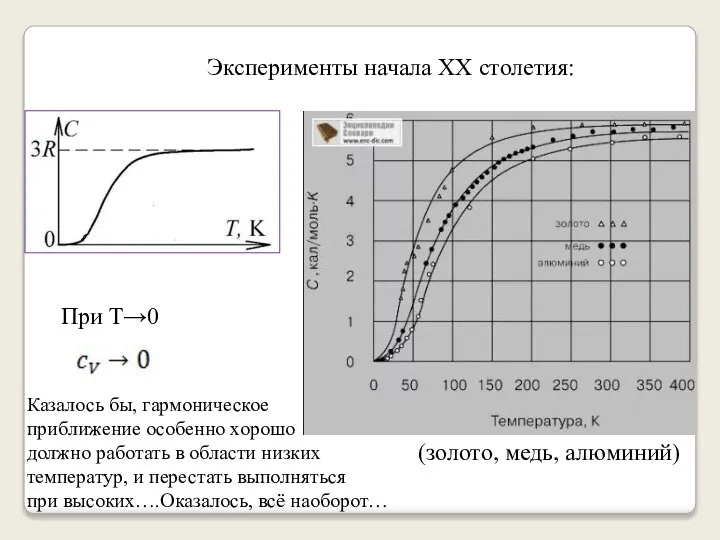
- 9. Эксперименты начала ХХ столетия: (золото, медь, алюминий) При Т→0 Казалось бы, гармоническое приближение особенно хорошо должно
- 10. 3. Квантовая теория теплоёмкости твердых тел Эйнштейна (1906 г.) Кристалл рассматривается как совокупность независимых гармонических осцилляторов,
- 11. б) Область низких температур: по экспоненциальному закону.
- 12. ВЫВОДЫ Теория Эйнштейна позволила объяснить стремление теплоёмкости к нулю при . Эйнштейн показал, что колебания механических
- 13. 4. Квантовая теория теплоёмкости твёрдых тел по Дебаю (1912 г.) . Модель упругого континуума (кристалл рассматривается
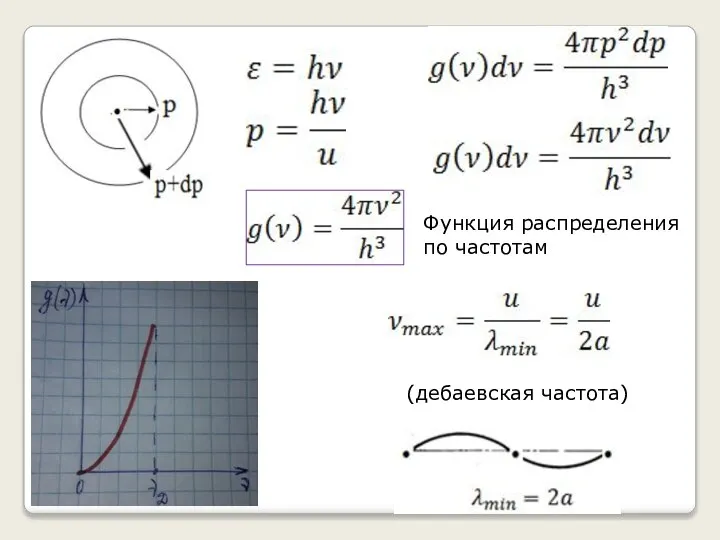
- 14. Функция распределения по частотам (дебаевская частота)
- 15. (полное число колебаний) Интерполяционная формула Дебая.
- 16. а) Область высоких температур: (Температура Дебая) (выполняется предельный переход к классическому результату и имеется согласие с
- 17. б) Область низких температур: При низких температурах возбуждаются низкие частоты колебаний, т.е. длинные волны. А длинная
- 18. При Т→0 теплоёмкость стремится к нулю, что согласуется с опытными данными.
- 20. Скачать презентацию













 Научное открытие России: Гравитационные волны
Научное открытие России: Гравитационные волны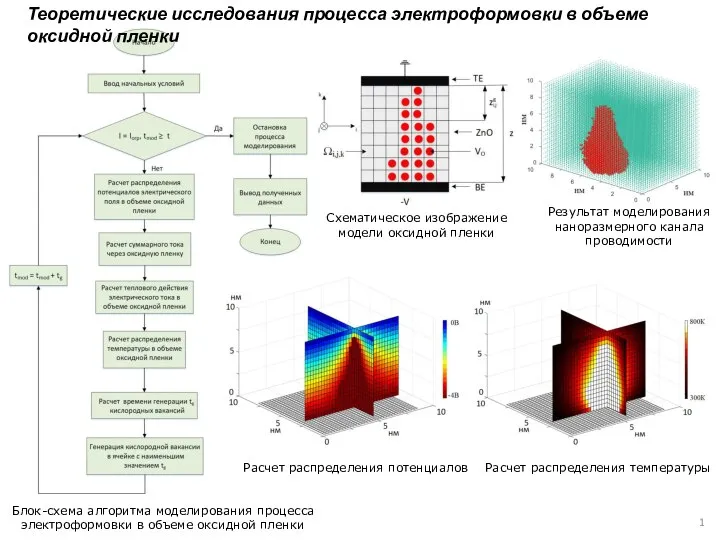 Модель исследования процесса электроформовки в объеме оксидной пленки
Модель исследования процесса электроформовки в объеме оксидной пленки Фотометрия Бугера, Ламберта, Бера
Фотометрия Бугера, Ламберта, Бера Деформированное состояние в точке. Обобщенный закон Гука. Лекция 10
Деформированное состояние в точке. Обобщенный закон Гука. Лекция 10 Презентация на тему Паровые машины
Презентация на тему Паровые машины  Электромагнитные колебания
Электромагнитные колебания Принципы действия различных типов двигателей. Двигатели внешнего сгорания
Принципы действия различных типов двигателей. Двигатели внешнего сгорания Техническое состояние трансмиссии автомобилей
Техническое состояние трансмиссии автомобилей Чувствительность взрывчатых систем к внешним воздействиям
Чувствительность взрывчатых систем к внешним воздействиям Закон сохранения механической энергии
Закон сохранения механической энергии Нефтегазовая и рудная геофизика. Сейсмические методы при изучении строения земной коры
Нефтегазовая и рудная геофизика. Сейсмические методы при изучении строения земной коры Реологиялық әдістер. Кернеу және пішін өзгерісі
Реологиялық әдістер. Кернеу және пішін өзгерісі Радиоволны. История открытия
Радиоволны. История открытия Выдающиеся физики
Выдающиеся физики Ядерная геофизика
Ядерная геофизика Визуальный и измерительный метод неразрушающего контроля. Электронный учебный курс
Визуальный и измерительный метод неразрушающего контроля. Электронный учебный курс Кинематика твердого тела/ Простейшие движения твердого тела
Кинематика твердого тела/ Простейшие движения твердого тела Сила трения. Сила упругости
Сила трения. Сила упругости Становление физиологии. Ятрофизика, ятромеханика
Становление физиологии. Ятрофизика, ятромеханика 840842
840842 Ангармонизм, упругость
Ангармонизм, упругость Взаимные превращения жидкостей и газов
Взаимные превращения жидкостей и газов Диадинамические токи
Диадинамические токи Презентация на тему Взаимодействие частиц вещества
Презентация на тему Взаимодействие частиц вещества  Выпускная бакалаврская работа Повышение безопасности труда при ремонте сельскохозяйственной техники
Выпускная бакалаврская работа Повышение безопасности труда при ремонте сельскохозяйственной техники Особенности эксплуатации оборудования для ТО и ТР колес и шин (урок 20-23)
Особенности эксплуатации оборудования для ТО и ТР колес и шин (урок 20-23) Блоки. Простые механизмы
Блоки. Простые механизмы Определение толщины зуба на любом радиусе
Определение толщины зуба на любом радиусе