Содержание
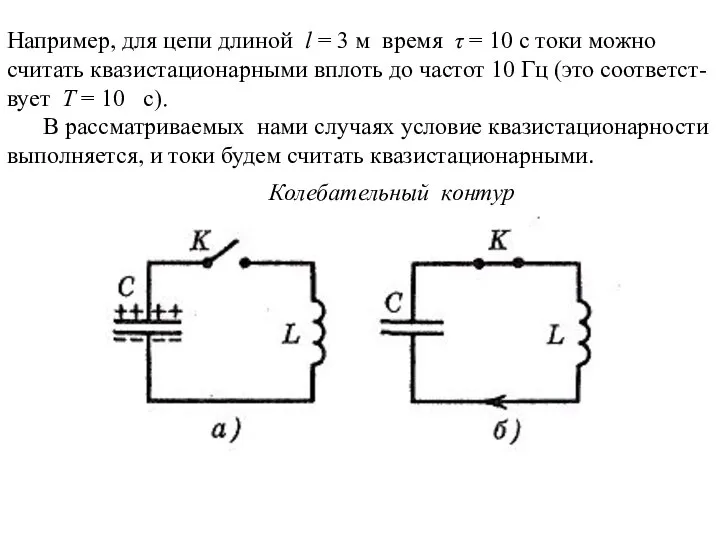
- 2. Например, для цепи длиной l = 3 м время τ = 10 с токи можно считать
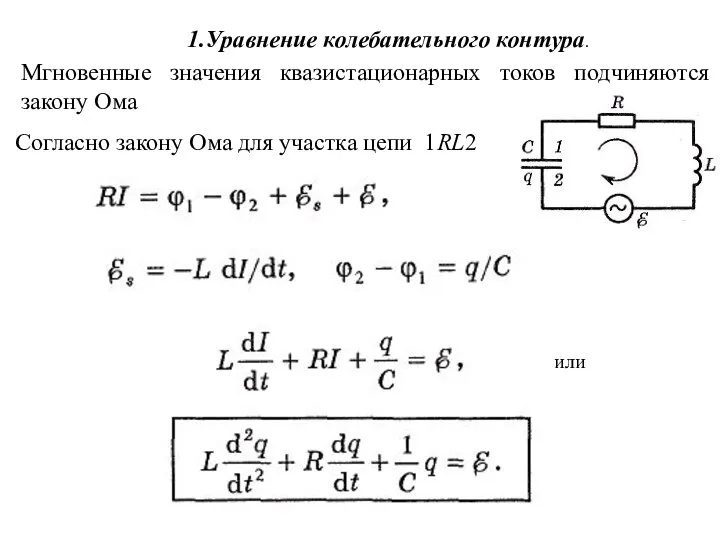
- 3. 1.Уравнение колебательного контура. Согласно закону Ома для участка цепи 1RL2 или Мгновенные значения квазистационарных токов подчиняются
- 4. Уравнению колебательного контура можно придать иной вид: 2.Свободные электрические колебания Свободные незатухающие колебания. Решением этого уравнения
- 5. 3. Свободные затухающие колебания амплитуда затухающих колебаний.
- 6. Напряжение на конденсаторе Ток в контуре или
- 7. Величины, характеризующие затухание 1.Коэффициент затухания β и время релаксации τ — время, за которое амплитуда колебаний
- 8. Если затухание мало,т.е. 3.Добротность колебательного контура − Q Чем меньше затухание, тем больше добротность Q При
- 9. β ≥ ω0 вместо колебаний будет происходить апериодичес-кий разряд конденсатора. Активное сопротивление контура, при котором наступает
- 10. Вынужденные электромагнитные колебания В контур включена внешняя переменная э. д. с. Уравнение колебаний в RCL контуре
- 11. Частное решение этого уравнения имеет вид qm — амплитуда заряда на конденсаторе ; ψ — разность
- 12. или Im — амплитуда тока, φ — сдвиг по фазе между током и внешней э. д.
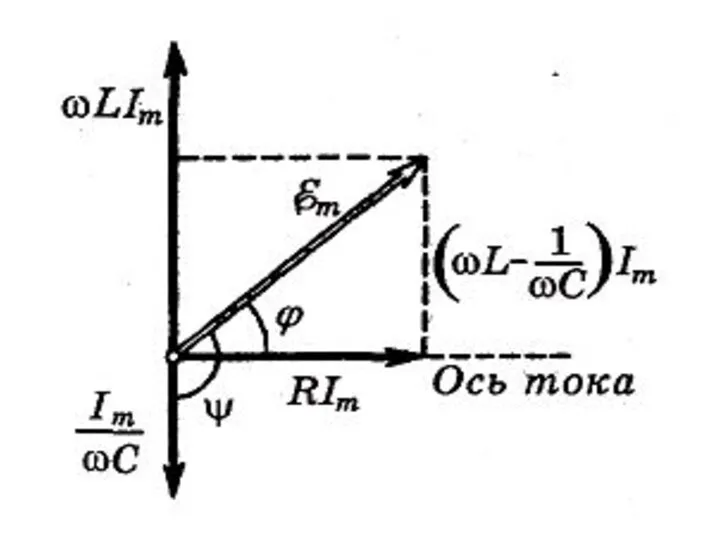
- 13. С помощью векторной диаграммы изобразим амплитуды напряжений как векторы, модули которых и найдем их векторную сумму,
- 15. Из прямоугольного треугольника этой диаграммы следуют выражения для . ,. .
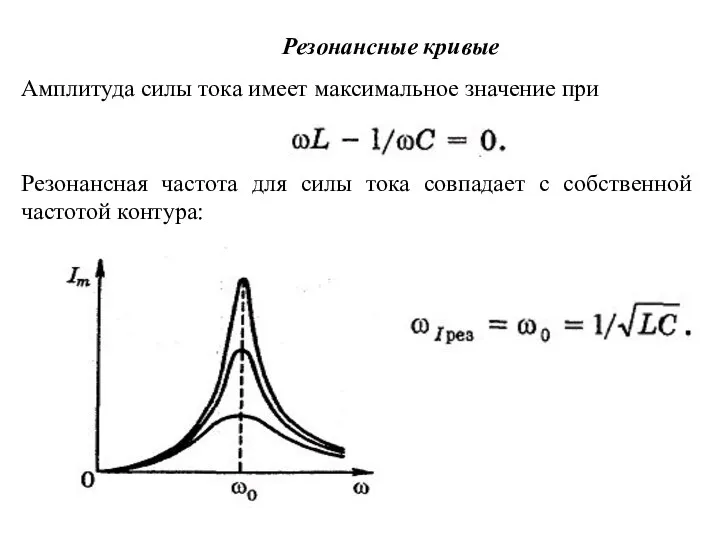
- 16. Резонансные кривые Амплитуда силы тока имеет максимальное значение при Резонансная частота для силы тока совпадает с
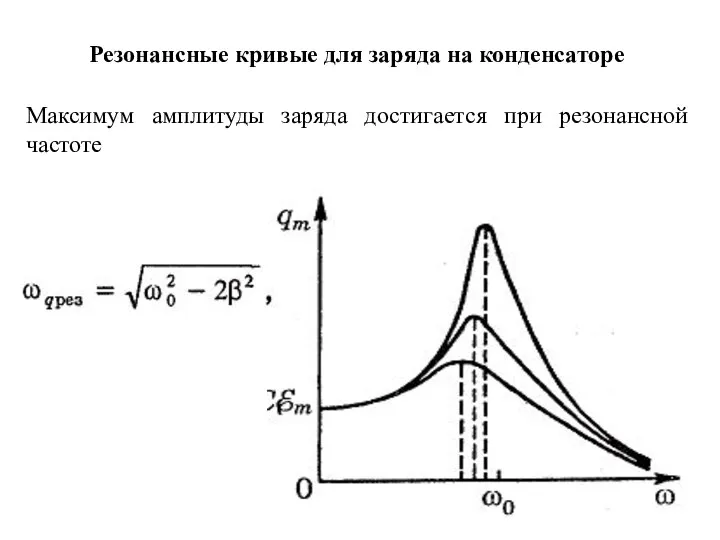
- 17. Резонансные кривые для заряда на конденсаторе Максимум амплитуды заряда достигается при резонансной частоте
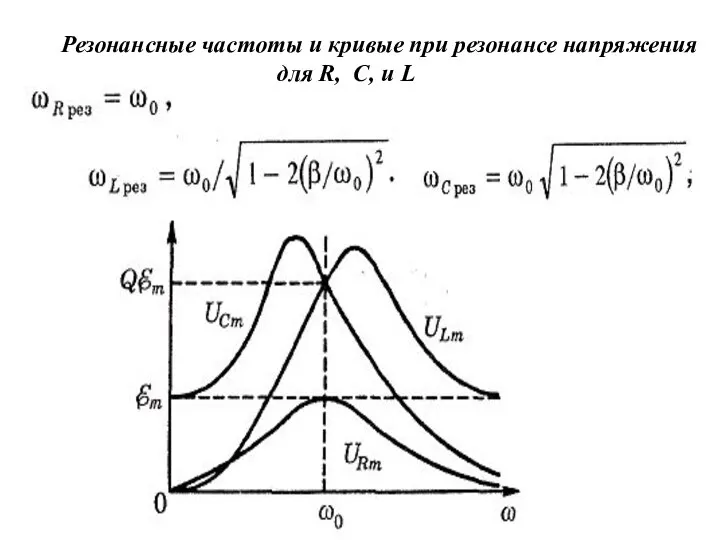
- 18. Резонансные частоты и кривые при резонансе напряжения для R, С, и L
- 19. Резонансные кривые и добротность Q. Слабое затухание, т. е. . В этом случае Добротность контура показывает
- 21. Скачать презентацию












 Метрология. Случайные погрешности: статистические методы оценивания
Метрология. Случайные погрешности: статистические методы оценивания Единицы работы электрического тока, применяемые на практике
Единицы работы электрического тока, применяемые на практике Оптические явления
Оптические явления МБОУ «Юхмачинская средняя общеобразовательная школа» Алькеевского муниципального района Республики Татарстан ФИЗИКА В ПРИРОДЕ
МБОУ «Юхмачинская средняя общеобразовательная школа» Алькеевского муниципального района Республики Татарстан ФИЗИКА В ПРИРОДЕ  Презентация на тему Электрическая цепь
Презентация на тему Электрическая цепь  Адиабатическое приближение
Адиабатическое приближение Лётные и эксплуатационные ограничения многодвигательного ВС DA-42. Тема 7
Лётные и эксплуатационные ограничения многодвигательного ВС DA-42. Тема 7 Физика. Физические явления
Физика. Физические явления Динер Никита Физика Инерция
Динер Никита Физика Инерция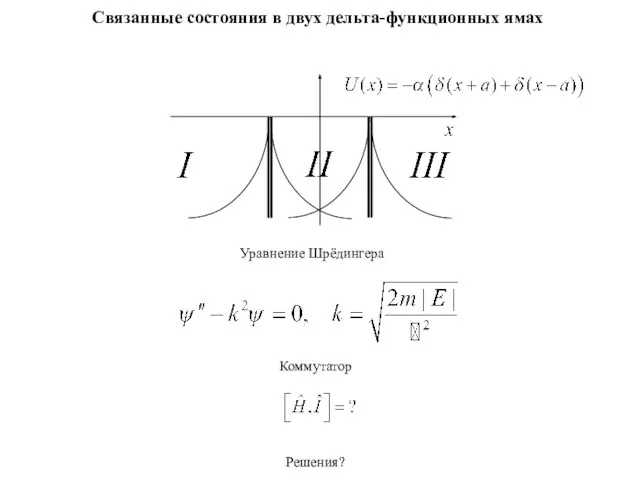 Связанные состояния в двух дельта - функционных ямах
Связанные состояния в двух дельта - функционных ямах Солнце, воздух и вода – наши лучшие друзья
Солнце, воздух и вода – наши лучшие друзья Револьверный станок
Револьверный станок Магнитное поле
Магнитное поле Внутренняя энергия. Работа в термодинамике. Количество теплоты
Внутренняя энергия. Работа в термодинамике. Количество теплоты Иллюзии и Физика. Вечная Борьба
Иллюзии и Физика. Вечная Борьба Теория пластин
Теория пластин Расчёт кругового поворота автомобиля
Расчёт кругового поворота автомобиля Сила трения
Сила трения Презентация на тему Кипение
Презентация на тему Кипение  Интерактивные лабораторные работы по физике
Интерактивные лабораторные работы по физике Нанотехнологии вокруг нас
Нанотехнологии вокруг нас Презентация на тему Сложение сил, направленных вдоль одной прямой. Равнодействующая сила
Презентация на тему Сложение сил, направленных вдоль одной прямой. Равнодействующая сила  Физика и В.О.В
Физика и В.О.В Способы увеличения подачи воздуха и топлива в цилиндры двигателя внутреннего сгорания (ДВС)
Способы увеличения подачи воздуха и топлива в цилиндры двигателя внутреннего сгорания (ДВС)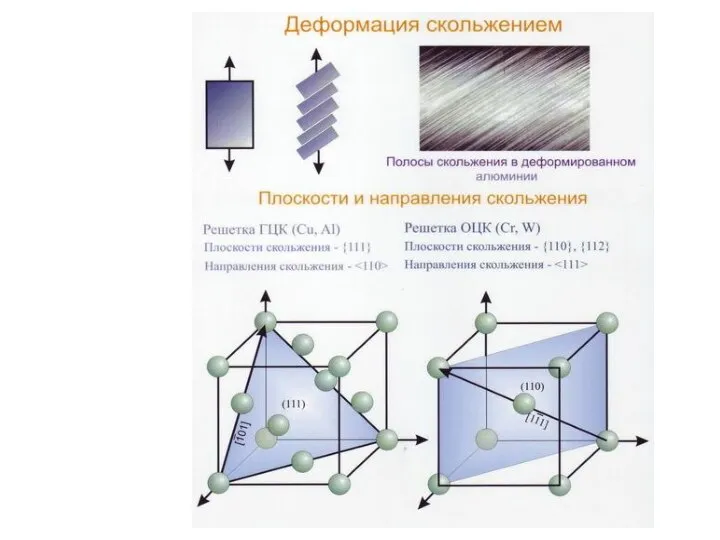 Пластическая деформация металлов
Пластическая деформация металлов ИК-спектроскопия
ИК-спектроскопия Техобслуживание
Техобслуживание Термодинамические системы и термодинамические параметры
Термодинамические системы и термодинамические параметры