Содержание
- 2. §5. Однородные уравнения Функция M(x , y) называется однородной степени m (или изме- рения m), если
- 3. Дифференциальное уравнение первого порядка y ′ = f(x , y) называется однородным относительно x и y,
- 4. §6. Уравнения, приводящиеся к однородным 1. Уравнения вида Рассмотрим уравнение (7) Если c1 = c2 =
- 5. а) Если Δ ≠ 0 , то (7) приводится к однородному уравнению. Действительно, если Δ ≠
- 6. б) Если Δ = 0 , то уравнение (7) приводится к уравнению с разделяющимися переменными. Действительно,
- 8. Скачать презентацию





 Презентация по физике "Что? Где? Когда?" -
Презентация по физике "Что? Где? Когда?" -  Магнитное поле. Сила Ампера
Магнитное поле. Сила Ампера Построение эпюр внутренних силовых факторов в рамах. Тема 8
Построение эпюр внутренних силовых факторов в рамах. Тема 8 Электростатика. Закон Кулона
Электростатика. Закон Кулона Необыкновенные оптические явления
Необыкновенные оптические явления Шум, вібрація. Електромагнітні поля різних частот як фактори навколишнього середовища, їх вплив на здоров’я, шляхи профілактики
Шум, вібрація. Електромагнітні поля різних частот як фактори навколишнього середовища, їх вплив на здоров’я, шляхи профілактики Байесовские процедуры принятия решений о состоянии объектов авиационного оборудования
Байесовские процедуры принятия решений о состоянии объектов авиационного оборудования Полное отражение
Полное отражение Агрегатные состояния вещества
Агрегатные состояния вещества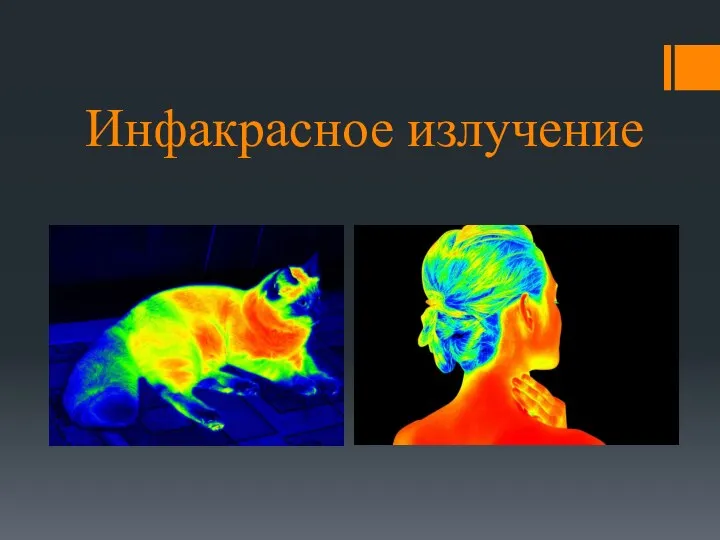 Инфакрасное излучение
Инфакрасное излучение Сопротивление материалов
Сопротивление материалов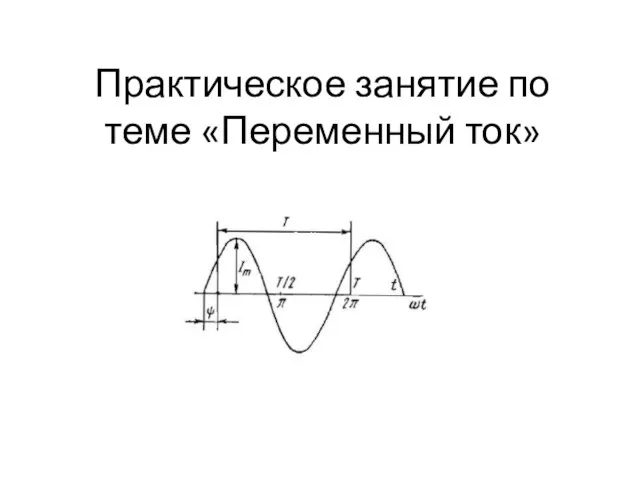 Переменный ток. Практическое занятие
Переменный ток. Практическое занятие Физика твердого тела
Физика твердого тела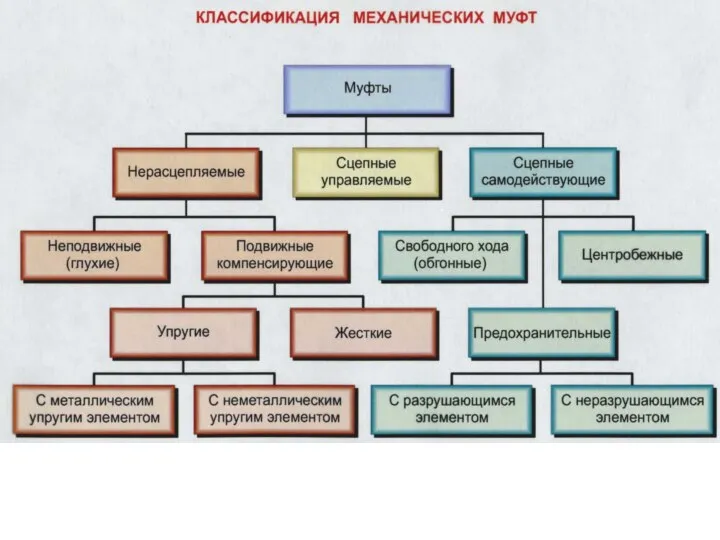 Классификация механических муфт
Классификация механических муфт Звуковые волны
Звуковые волны Семинар 15. Изгибные колебания стержня (самостоятельная)
Семинар 15. Изгибные колебания стержня (самостоятельная) Действие жидкости и газа на погруженное в них тело
Действие жидкости и газа на погруженное в них тело Метод размерностей
Метод размерностей Теория управления. Тест
Теория управления. Тест Производная в физике и технике
Производная в физике и технике Энергия
Энергия Электрическая цепь. Основные законы
Электрическая цепь. Основные законы Схема процесса работы кровельной машины ЛУЧ
Схема процесса работы кровельной машины ЛУЧ Давление жидкости на стенки и на дно сосуда
Давление жидкости на стенки и на дно сосуда Первичные и вторичные параметры длинной линии. Лекция Д1
Первичные и вторичные параметры длинной линии. Лекция Д1 Уровнемеры. Задачи и способы измерения и контроля уровня жидкости
Уровнемеры. Задачи и способы измерения и контроля уровня жидкости Своя игра. 7 класс
Своя игра. 7 класс Математическое моделирование процесса теплопередачи в атмосферном газификаторе СПГ
Математическое моделирование процесса теплопередачи в атмосферном газификаторе СПГ