Электроника

ФИЗИЧЕСКИЕ ОСНОВЫ ПОЛУПРОВОДНИКОВОЙ ЭЛЕКТРОНИКИ

Удельное электрическое сопротивление ρ – промежуточное положение между проводниками и диэлектриками.
Высокая чувствительность их электропроводности к добавлению примесей других веществ даже в незначительных количествах.
Сильная, нелинейная, обратная зависимость удельного сопротивления от температуры.
Зависимость удельного сопротивления от различного рода излучений.
Определяющие свойства полупроводников

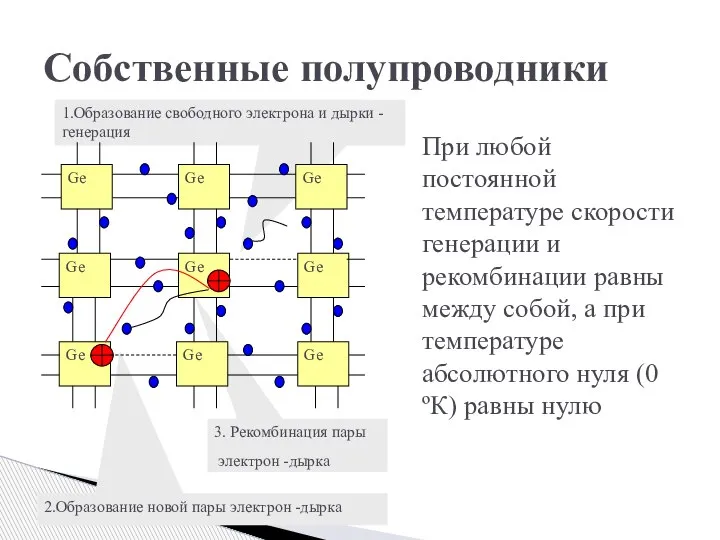
При любой постоянной температуре скорости генерации и рекомбинации равны между собой, а при температуре абсолютного нуля (0 ºК) равны нулю
Собственные полупроводники

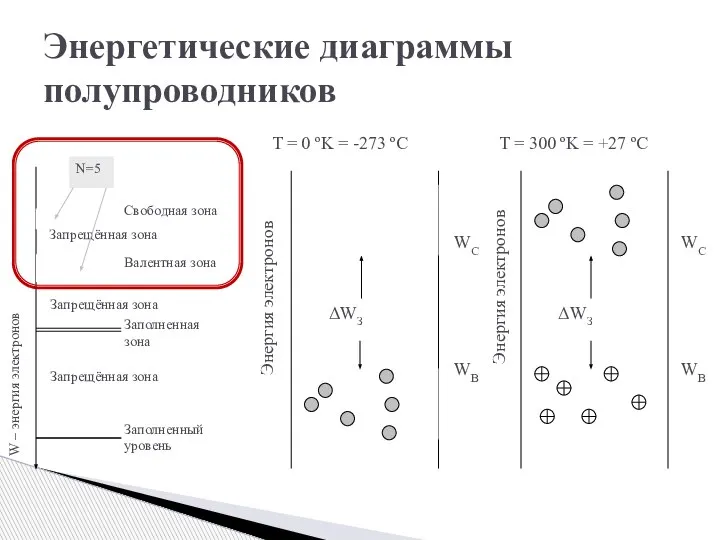
Энергетические диаграммы полупроводников
Энергия электронов

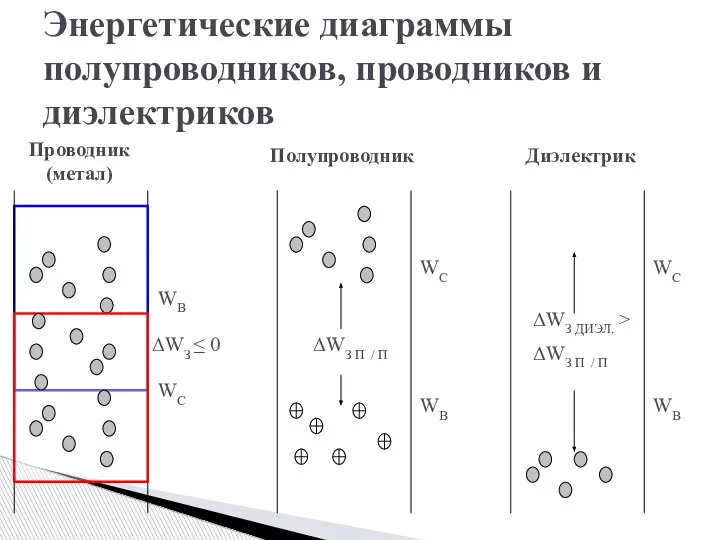
Энергетические диаграммы полупроводников, проводников и диэлектриков
Проводник (метал)
Полупроводник
Диэлектрик

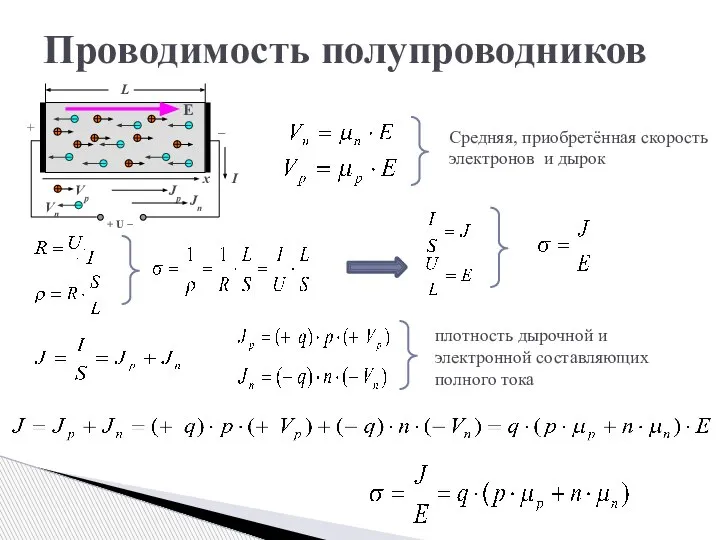
Проводимость полупроводников
Средняя, приобретённая скорость электронов и дырок
плотность дырочной и электронной составляющих полного тока

Поскольку у собственных полупроводников
, то:
Здесь и далее индекс i означает собственный полупроводник.
Электропроводность собственных полупроводников

Функция распределения
Ферми-Дирака
Fn(W) + Fp(W) = 1,
Fp(W) = 1 - Fn(W),
Fp(W) = 1/(1 + exp((WF - W) / kT ))
Fn(W) = 1/(1 + exp((W - WF) / kT ))
Вероятность заполнения электроном энергетического уровня с энергией W, при заданной температуре T, количественно выражается функцией распределения Ферми-Дирака:
k – постоянная Больцмана
T – абсолютная температура
WF – уровень Ферми.
Fp(W) – вероятность нахождения дырки на энергетическом уровне W.
Уровень Ферми – энергетический уровень равно-вероятный как для электрона, так и для дырки.

Свойства функции распределения
Ферми-Дирака
При T=0 функция Ферми превращается в ступенчатую.
Для собственного полупроводника уровень Ферми лежит в середине запрещённой зоны, т.к. функция вероятности симметрична относительно него при любой фиксированной температуре.
Функция Ферми имеет смысл только в валентной и свободной зонах, т.к. в запрещённой зоне носители заряда находиться не могут.

Энергетические уровни зоны проводимости, а также и валентной зоны распределены неравномерно, т.е. их плотность зависит от энергии.
P(W) – число энергетических уровней в зоне проводимости, попадающих в единичный, бесконечно малый энергетический интервал dW. Т.е. P(W) – функция, характеризующая плотность энергетических уровней.
dW·P(W) – число уровней в элементарной полосе dW.
Fn(W) – вероятностью заполнения энергетических уровней.
Тогда количество электронов, занимающих разрешённые энергетические уровни в некоторой полосе dW
dni = P(W)·Fn(W)·dW.
Определение концентрации электронов и дырок в собственном полупроводнике

Полное число электронов, приходящихся на 1 см3 вещества и занимающих энергетические уровни в полосе энергий от W1 до W2 будет равно:
Аналогичным образом для концентрации дырок валентной зоны получим:
В обоих случаях интегрирование ведётся по всей ширине зоны проводимости (сonductivity) или валентной (valency) зоны.
В результате интегрирования получим:
Определение концентрации электронов и дырок в собственном полупроводнике (продолжение)
NС и NV – эфективная плотность состояний (на 1 см3) в зоне проводимости и валентной зоне соответственно.
h = 4,14·10-15 эв·сек – постоянная Планка.
mn и mp – эффективная масса электрона и дырки соответственно.

В большинстве практических случаев можно считать, что mn = mp = m – массе электрона в состоянии покоя. Тогда:
Положив далее, что ΔWз = Wc -Wv и учитывая, что в собственном полупроводнике ni = pi , выражения для концентрации электронов и дырок можно привести к виду:
Определение концентрации электронов и дырок в собственном полупроводнике (продолжение)

При этих условиях уровень Ферми лежит точно посередине запрещённой зоны, т.е.
WFi = (Wс-Wv) / 2.
Подставляя найденное значение концентрации ni в выражение для проводимости собственного полупроводника придем к следующей зависимости:
Определение концентрации электронов и дырок в собственном полупроводнике (продолжение)

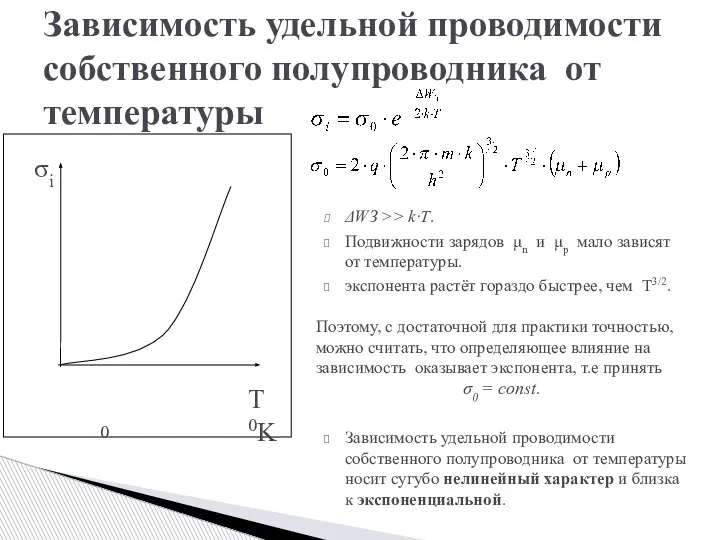
Зависимость удельной проводимости собственного полупроводника от температуры
0
ΔWЗ >> k·T.
Подвижности зарядов μn и μp мало зависят от температуры.
экспонента растёт гораздо быстрее, чем T3/2.
Поэтому, с достаточной для практики точностью, можно считать, что определяющее влияние на зависимость оказывает экспонента, т.е принять
σ0 = const.
Зависимость удельной проводимости собственного полупроводника от температуры носит сугубо нелинейный характер и близка к экспоненциальной.

Ион примеси не является носителем заряда, он неподвижен – это не дырка.
Полупроводник типа – n или электронного типа
Примеси отдающие лишний электрон и обусловливающие электронную проводимость называются донорными.
Процесс введения примеси в полупроводник называется легированием, а примесный полупроводник - легированным.

Уравнение n-полупроводника
Концентрации электронов и дырок в полупроводнике типа n рассчитываются также на основе статистики Ферми-Дирака.
где WFn – уровень Ферми в полупроводнике типа n, определяемый выражением
Величина Nд представляет собой концентрацию доноров. Из выражения видно, что уровень Ферми лежит ниже уровня дна зоны проводимости. Произведение концентраций электронов и дырок равно:
Уравнение полупроводника:

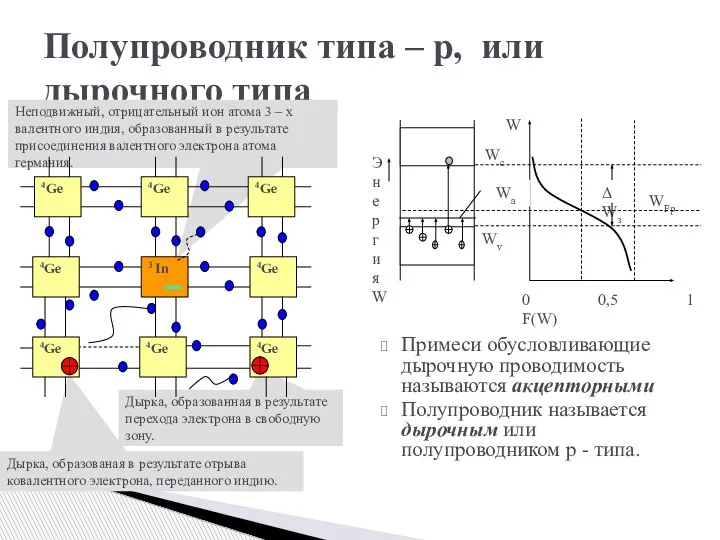
Примеси обусловливающие дырочную проводимость называются акцепторными
Полупроводник называется дырочным или полупроводником p - типа.
Полупроводник типа – p, или дырочного типа

Уравнение p-полупроводника
Концентрации электронов и дырок в полупроводнике типа p рассчитываются также на основе статистики Ферми-Дирака.
где WFp – уровень Ферми в полупроводнике типа p, определяемый выражением
Величина Nа представляет собой концентрацию акцепторов.
Так же как и для n – полупроводника, для полупроводников типа p справедливо равенство:
Это равенство означает, что произведение концентраций электронов и дырок при данной температуре T для данного полупроводника постоянно и не зависит от характера и количества примесей.

Следствие из уравнения полупроводника
В силу симметрии выражений, определяющих концентрацию основных и неосновных носителей заряда в примесных полупроводниках, независимо от типа проводимости, их можно записать в следующем виде:
где WF – уровень Ферми, определяемый для соответствующего типа полупроводника
Поделив эти выражения друг на друга, приняв при этом n = ni2 / p и p = ni2 / n, можно привести их к следующему виду:
где WFi = (Wc - Wv) / 2 – уровень Ферми в собственном полупроводнике, а WF – уровень Ферми в соответствующем примесном полупроводнике.
Учитывая, что энергия электрона (дырки) W = q·φ, последние выражения для дырок и электронов соответственно можно привести к виду:
φF i – потенциал Ферми в (вольтах) собственного полупроводника,
φF - потенциал Ферми в (вольтах) соответствующего собственного полупроводника,
φT = k·T/q – температурный потенциал (в вольтах). При комнатной температуре φT =0,025В.

Следствие из уравнения полупроводника (продолжение)
Заменим потенциал Ферми в собственном полупроводнике – φFi потенциалом середины запрещённой зоны примесного полупроводника - φE, что практически одно и то же, т.к. φFi ≈ φE.
Тогда:
Из этих выражений непосредственно следует:
φFn = φE + φT · ln(n / n i ) – для полупроводников n – типа уровень Ферми смещён от середины запрещённой зоны вверх по диаграмме к свободной зоне на величину ln(n / n i ).
φFp = φE - φT · ln(p / n i ) – для полупроводников p – типа уровень Ферми смещён от середины запрещённой зоны вниз по диаграмме к валентной зоне на величину ln(p / n i ) .

в электронном полупроводнике n>>p,
σn ≈ q·n·μn
в дырочном полупроводнике p>>n,
σp ≈ q·p·μp
Электропроводность примесных полупроводников

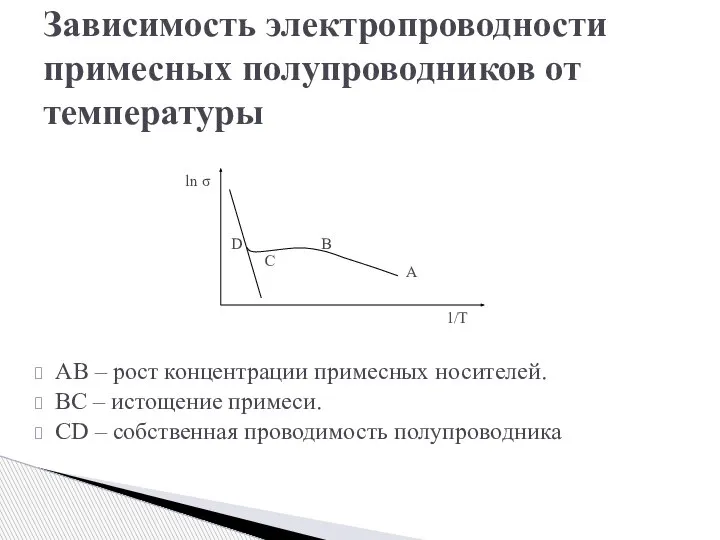
AB – рост концентрации примесных носителей.
BC – истощение примеси.
CD – собственная проводимость полупроводника
Зависимость электропроводности примесных полупроводников от температуры