Содержание
- 2. Электростатика – раздел теории электричества, изучающий взаимодействие неподвижных друг относительно друга электрических зарядов и связанные с
- 3. Существуют два вида электрических зарядов: заряды подобные тем, которые возникают на стекле, потертом о шелк -
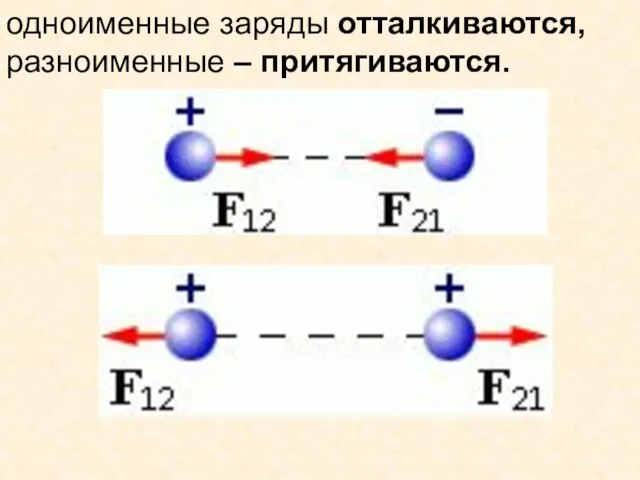
- 4. одноименные заряды отталкиваются, разноименные – притягиваются.
- 5. Если поднести заряженное тело (с любым зарядом) к легкому – незаряженному, то между ними будет притяжение
- 6. Таким образом, всякий процесс заряжения есть процесс разделения зарядов. Сумма зарядов не изменяется, заряды только перераспределяются.
- 7. Закон сохранения заряда Алгебраическая сумма электрических зарядов любой изолированной (или замкнутой) системы остается постоянной, какие бы
- 8. Электрические заряды не существуют сами по себе, а являются внутренними свойствами элементарных частиц – электронов, протонов
- 9. Заряд q любого тела составляет целое кратное от элементарного электрического заряда (n – целое число):
- 10. Земля имеет отрицательный заряд q= - 6 * 105Кл это установлено по измерению напряженности электростатического поля
- 11. 2. Взаимодействие электрических зарядов в вакууме. Точечным зарядом (q) называется заряженное тело, размеры которого пренебрежительно малы
- 12. Закон Кулона сила взаимодействия точечных зарядов в вакууме пропорциональна величине зарядов и обратно пропорциональна квадрату расстояния
- 13. В СИ единица заряда 1 Кл = 1А * 1с где ε0 – электрическая постоянная; 4π
- 14. Электрическая постоянная относится к числу фундаментальных физических констант и равна Элементарный заряд в СИ: Отсюда следует,
- 15. Закон Кулона векторной форме: где F1 – сила, действующая на заряд q1 F2 – сила, действующая
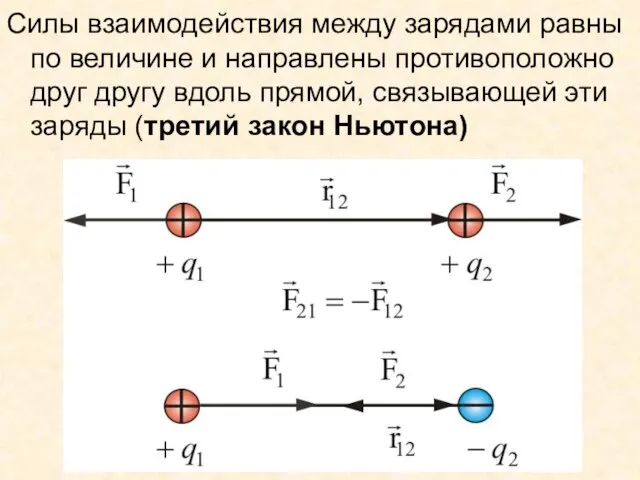
- 16. Силы взаимодействия между зарядами равны по величине и направлены противоположно друг другу вдоль прямой, связывающей эти
- 17. Если заряды не точечные, то в такой форме закон Кулона использовать нельзя - нужно интегрировать по
- 18. Закон Кулона в основных чертах подобен закону всемирного тяготения Ньютона Различие заключаются в том, что заряженные
- 19. Сила кулоновского притяжения между электроном и протоном в атоме водорода в 1039 раз больше их гравитационного
- 20. 3. Электростатическое поле. Напряженность электростатического поля Теории взаимодействия: теория дальнодействия – Ньютон, Ампер теория близкодействия –
- 21. Вокруг заряда всегда есть электрическое поле, основное свойство которого заключается в том, что на всякий другой
- 22. ЭМП – есть не абстракция, а объективная реальность – форма существования материи, обладающая определенными физическими свойствами,
- 23. Силовой характеристикой поля создаваемого зарядом q является отношение силы действующей на заряд к величине этого заряда
- 24. Напряженность в векторной форме здесь r – расстояние от заряда до точки, где мы изучаем это
- 25. Вектор напряженности электростатического поля равен силе, действующей в данной точке на помещенный в нее пробный единичный
- 26. В СИ размерность напряженности:
- 27. 4. Сложение электростатических полей. Принцип суперпозиции Если поле создается несколькими точечными зарядами, то на пробный заряд
- 28. Результирующая сила: – это принцип суперпозиции или независимости действия сил
- 29. Результирующая напряженность поля в точке, где расположен пробный заряд, так же подчиняется принципу суперпозиции: Напряженность результирующего
- 30. Пример 1 т. е. и
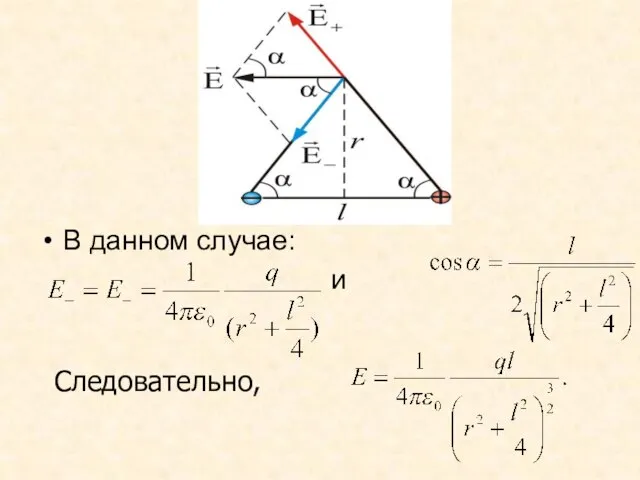
- 31. В данном случае: и Следовательно,
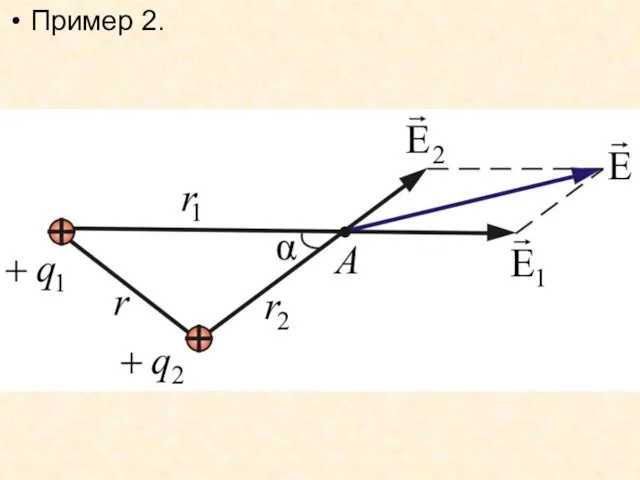
- 32. Пример 2.
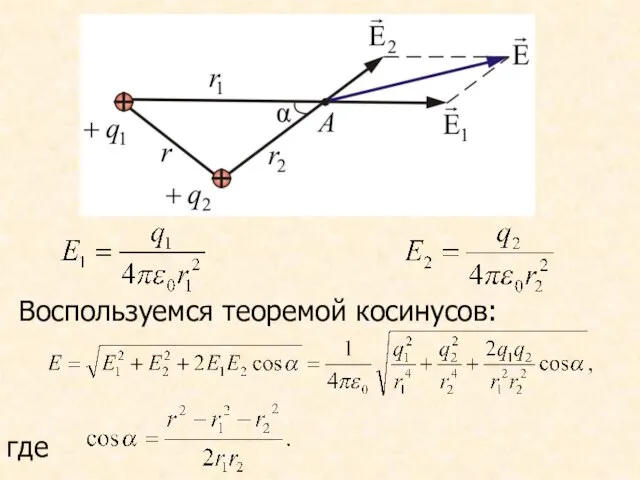
- 33. Воспользуемся теоремой косинусов: где
- 34. Если поле создается не точечными зарядами, то используют обычный в таких случаях прием. Тело разбивают на
- 35. Плотности заряда: – линейная плотность заряда, измеряется в Кл/м; - поверхностная плотность заряда измеряется в Кл/м2;
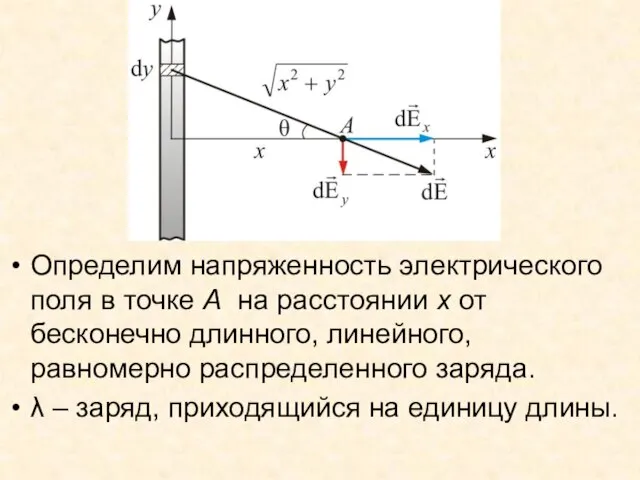
- 36. Определим напряженность электрического поля в точке А на расстоянии х от бесконечно длинного, линейного, равномерно распределенного
- 37. Считаем, что х – мало по сравнению с длиной проводника. Элемент длины dy, несет заряд dq
- 38. Вектор имеет проекции dEx и dEy причем Т.к. проводник бесконечно длинный, а задача симметричная, то у
- 39. Тогда Теперь выразим y через θ. Т.к. То и тогда
- 40. Напряженность электрического поля линейно распределенных зарядов изменяется обратно пропорционально расстоянию до заряда.
- 41. 5. Электростатическое поле диполя Электрическим диполем называется система двух одинаковых по величине, но разноименных точечных зарядов,
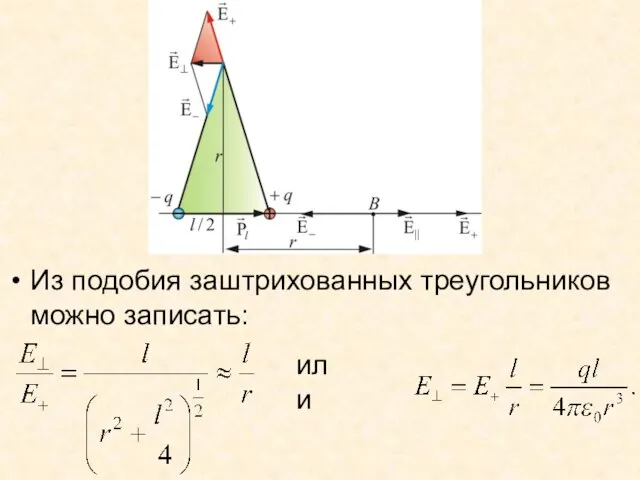
- 42. Пример 1. Найдем Е⊥ в точке А на прямой, проходящей через центр диполя и перпендикулярной к
- 43. Из подобия заштрихованных треугольников можно записать: или
- 44. Электрический момент диполя (или дипольный момент) – произведение положительного заряда диполя на плечо . Направление совпадает
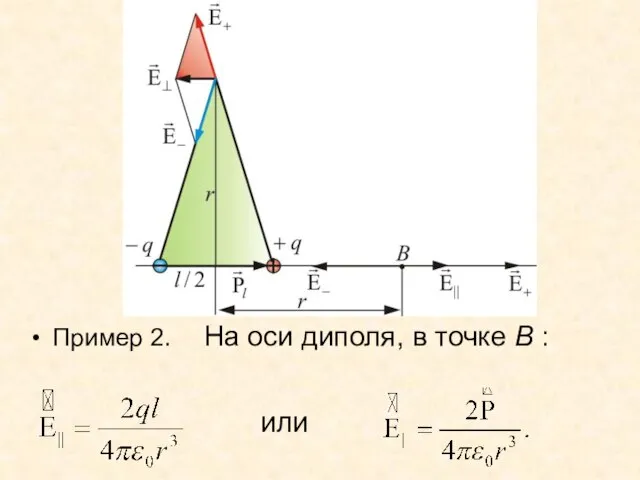
- 45. Пример 2. На оси диполя, в точке В : или
- 47. Скачать презентацию






















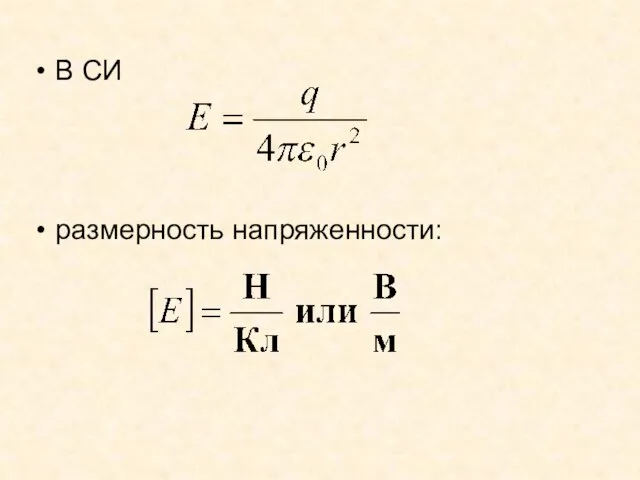








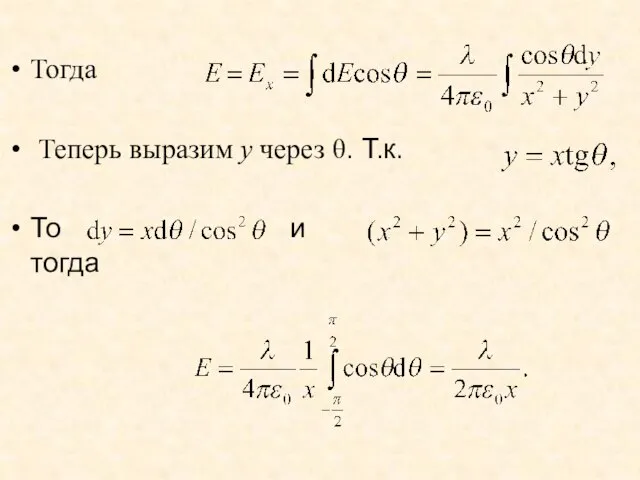




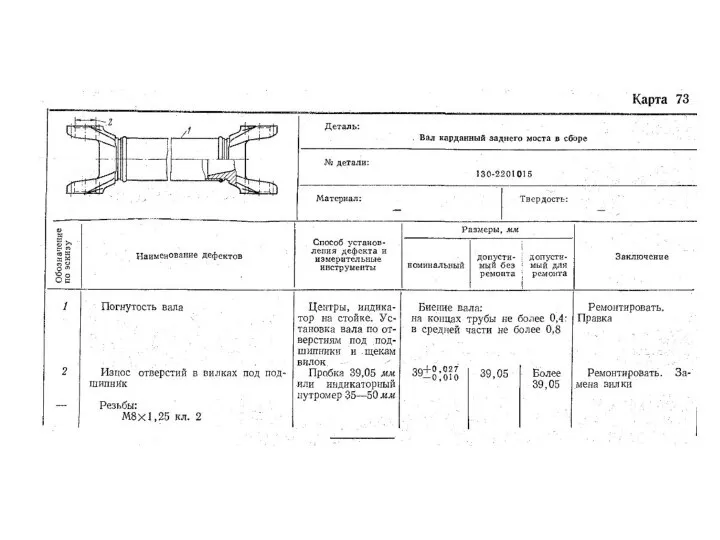 Ремонт автомобилей. Детали
Ремонт автомобилей. Детали zakony_nyutona_9_k
zakony_nyutona_9_k Радиоволны. Рудольф Генрих
Радиоволны. Рудольф Генрих Динамика. Законы Ньютона: область применимости
Динамика. Законы Ньютона: область применимости Бесконтактная передача электроэнергии
Бесконтактная передача электроэнергии Валы и оси
Валы и оси Приходченко ФЕР-2032и
Приходченко ФЕР-2032и Презентация на тему Собирающие линзы
Презентация на тему Собирающие линзы  Винт Архимеда
Винт Архимеда Физика за чашкой чая. Тепловые явления. Проще простого
Физика за чашкой чая. Тепловые явления. Проще простого Давление твердых тел
Давление твердых тел Электризация тел и строение атома
Электризация тел и строение атома Презентация на тему Момент силы (7 класс)
Презентация на тему Момент силы (7 класс)  Механические колебания. Звуковые волны. Акустика
Механические колебания. Звуковые волны. Акустика Создание трехмерных деталей и сборки
Создание трехмерных деталей и сборки Электрометр. Опыты Ломоносова
Электрометр. Опыты Ломоносова Основные понятия и аксиомы динамики. Понятие о трении
Основные понятия и аксиомы динамики. Понятие о трении Метрология. Случайные погрешности: статистические методы оценивания
Метрология. Случайные погрешности: статистические методы оценивания Оптимизация методики разделения лечебного препарата Clopidogrel Hydrogen Sulfate с сопутствующей примесью (А)
Оптимизация методики разделения лечебного препарата Clopidogrel Hydrogen Sulfate с сопутствующей примесью (А) Презентация на тему Решение задач по теме «Фотоэффект»
Презентация на тему Решение задач по теме «Фотоэффект»  Атомная энергетика. Биологическое действие радиации. Термоядерная реакция Учитель физики Борисова С.А. ГБОУ СОШ №924
Атомная энергетика. Биологическое действие радиации. Термоядерная реакция Учитель физики Борисова С.А. ГБОУ СОШ №924 Паралельне з’єднання провідників. Урок 51
Паралельне з’єднання провідників. Урок 51 Потенциал электрического поля. Разность потенциалов
Потенциал электрического поля. Разность потенциалов Радиоактивные превращения атомных ядер
Радиоактивные превращения атомных ядер Простые механизмы
Простые механизмы Первый закон Ньютона
Первый закон Ньютона Презентация на тему Постоянные магниты
Презентация на тему Постоянные магниты  Уравнения переменного тока. Задачи
Уравнения переменного тока. Задачи