решетки
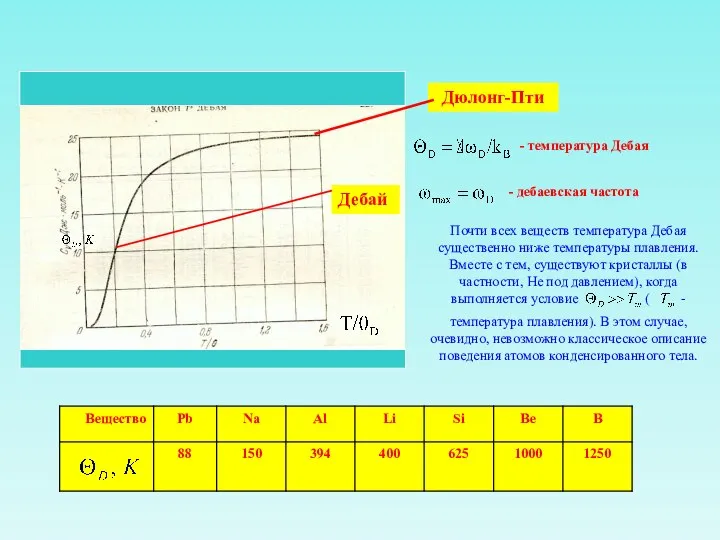
В конденсированном теле при нулевой температуре фононы отсутствуют (положение атомов в узлах – основное состояние конденсированного тела - является вакуумом для фононов), а их появление связано с нагревом тела
С ростом температуры число фононов растет и их число в коллективном движении атомов является весьма большой (макроскопической) величиной. Таким образом, возникает картина большого числа фононов как носителей коллективного возбуждения конденсированного тела. Поскольку фононы могут возбуждаться поодиночке, а значит, имеют целый спин, то они являются бозе-частицами и подчиняются в ансамбле статистике Бозе-Эйнштейна. Следует также заметить, что введение фононов только тогда имеет смысл, если они между собой либо вообще не взаимодействуют, либо взаимодействуют слабо. Следовательно, сам ансамбль фононов можно рассматривать как газ. В этом случае общую энергию конденсированного тела можно рассматривать как сумму энергии основного состояния – энергия связи атомов в положении равновесия и энергия нулевых (квантовых) колебаний атомов (вакуум для фононов) и суммы энергий отдельных фононов:
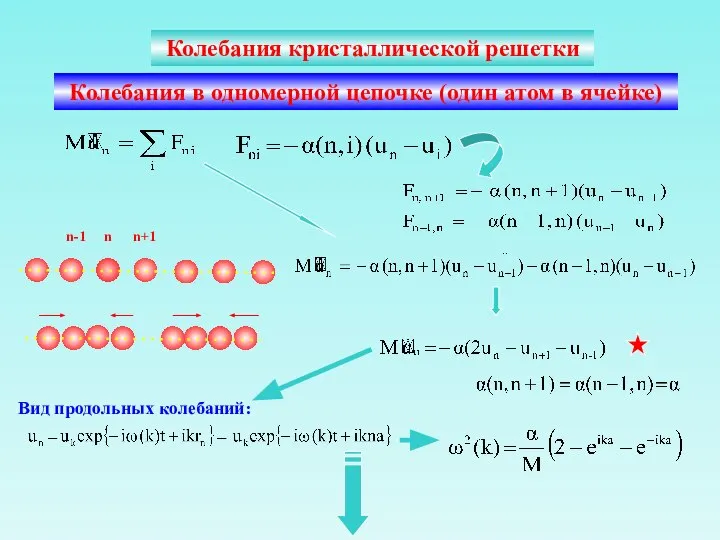
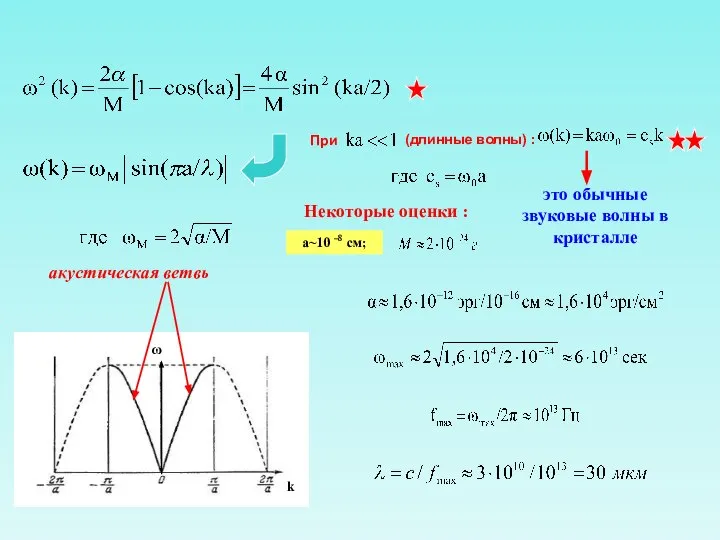
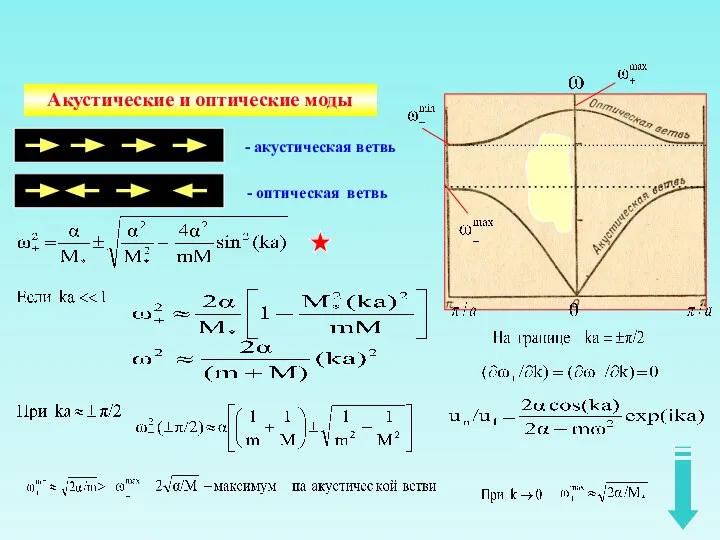
В кристаллах может быть несколько типов фононов (например, акустические и оптические, причем при наличии в ячейке j атомов – 3j типов фононов








 Кинетическая и потенциальная энергия. Открытый урок по физике
Кинетическая и потенциальная энергия. Открытый урок по физике Фазовые переходы
Фазовые переходы Определить импульс фотона с энергией
Определить импульс фотона с энергией Энергия. Работа. Мощность
Энергия. Работа. Мощность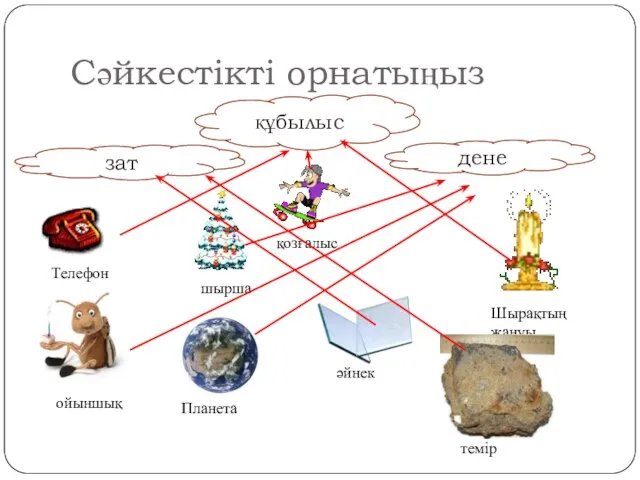 Физикалық шама
Физикалық шама Электромагнитные волны
Электромагнитные волны Стартовый ускоритель
Стартовый ускоритель Явления тяготения. Сила тяжести
Явления тяготения. Сила тяжести Электрическая винто-моторная установка для БПЛА С
Электрическая винто-моторная установка для БПЛА С Эрнест Резерфорд
Эрнест Резерфорд Физика в эпоху античности
Физика в эпоху античности Исследование цепей с последовательным и параллельным соединением резисторов
Исследование цепей с последовательным и параллельным соединением резисторов Параметры сопряжения деталей
Параметры сопряжения деталей Системы АРУ. Примеры и реализация
Системы АРУ. Примеры и реализация Биологическое действие радиоактивных излучений
Биологическое действие радиоактивных излучений Механическая работа
Механическая работа Электромагнитные явления
Электромагнитные явления Использование электромагнитной индукции
Использование электромагнитной индукции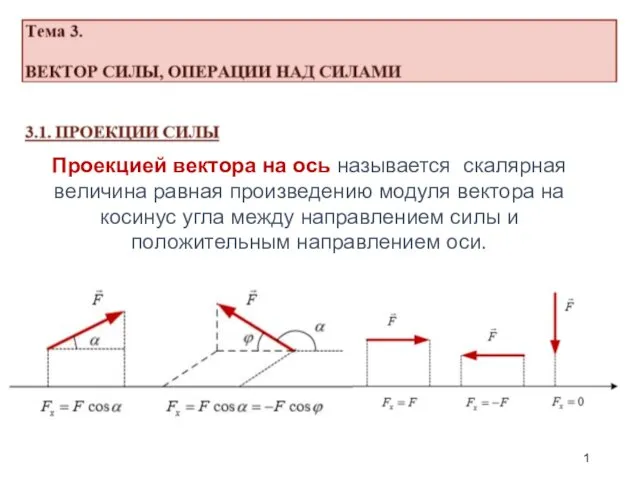 Вектор силы, операции над силами
Вектор силы, операции над силами M_P_Rezistivnye_M (1)
M_P_Rezistivnye_M (1) Радіо. Історія виникнення радіозв'язку
Радіо. Історія виникнення радіозв'язку Математическое введение
Математическое введение Фотоэффект
Фотоэффект Презентация ученицы 11 «А» класса Очеретиной Александры
Презентация ученицы 11 «А» класса Очеретиной Александры Последовательность операций
Последовательность операций Измерение температуры
Измерение температуры Шалаев Хиггс
Шалаев Хиггс Три состояния вещества
Три состояния вещества