Элементы специальной теории относительности

Некоторые эксперименты с “драматическими” результатами
a) Заряженная частица и провод с током
В лабораторной системе провод не заряжен,
но в нем существует ток i, который создает
магнитное поле, в котором на частицу действует
сила Лоренца, заставляющая притягиваться
частицу к проводу.
НО! В системе, связанной с частицей этой
силы НЕТ! Так как частица покоится!
Как же так? Выходит, что факт притяжения
(или его отсутствия) зависит от точки зрения
наблюдателя. НЕ МОГУ С ЭТИМ СМИРИТЬСЯ!

б) Предельная скорость

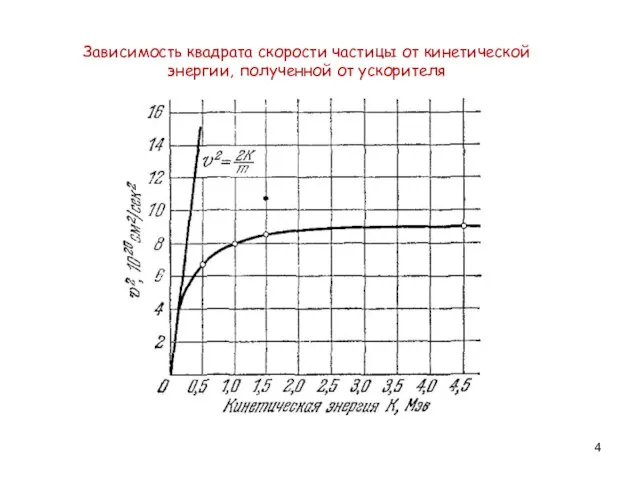
Зависимость квадрата скорости частицы от кинетической
энергии, полученной от ускорителя

в) Опыт Майкельсона и Морли (1887 г).

II. Преобразования Лоренца
Рассмотрим поверхность фронта световой волны от точечного
источника света, находящегося в начале координат. Это сфера
и ее уравнение:
Но в другой системе (двигающейся со скоростью ) скорость света
такая же, следовательно и уравнение такое же:
Если преобразования Галилея верны, то какое-то из этих уравнений
точно не верно! Действительно, если подставить преобразования:
получим:
Но, если положить, что
То:
А вот это подойдет:

Сложение скоростей
Частные случаи, ломающие мировоззрение:

Преобразование длин и временных интервалов

III. Что же там на самом деле в динамике?
Если импульс по-прежнему будем определять как
то при переходе в другую “быструю” инерциальную систему он
сохраняться не будет!!!
Выполнение закона сохранения количества движения можно
обеспечить лишь приняв, что:
Эх, не побоимся и признаем, что:
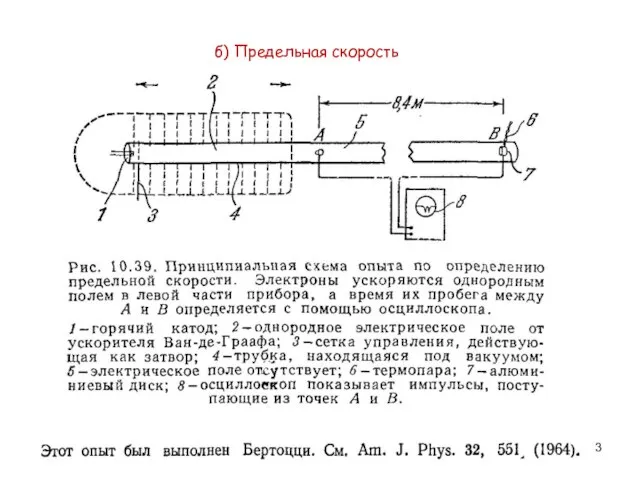
Тогда понятен результат
эксперимента Бертоцци!

Будем последовательны и наложим руки на энергию!
Так как: то:
После подстановки получим: или:
Здесь ПОЛНАЯ энергия:
Кроме кинематического есть и другой инвариант: