Содержание
- 2. Основные положения: электроны в атоме (в твердом теле) подчиняются законам волновой, квантовой механики. энергия электронов в
- 3. Элементы зонной теории твердых тел. Энергетические зоны. В изолированном атоме состояние электрона определяется набором 4-х квантовых
- 4. Зонная теория твердых тел Число энергетических уровней в атоме равно номеру периода: Орбитальное квантовое число определяет
- 5. По принципу Паули в атоме не может быть двух одинаковых электронов, т.е. находящихся в одинаковых состояниях
- 6. Расщепление энергетических уровней в зависимости от расстояния между атомами. Зонная теория твердых тел
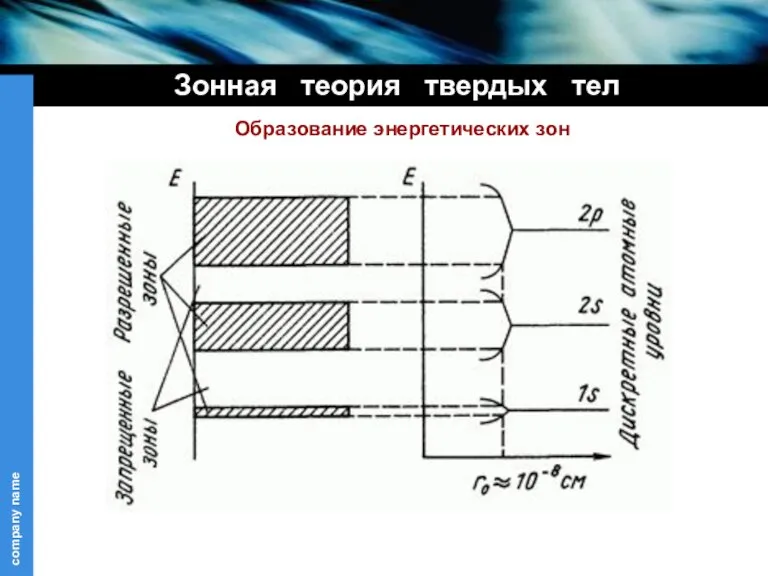
- 7. Образование энергетических зон Зонная теория твердых тел
- 8. Проводники, полупроводники и диэлектрики в зонной теории твердого тела Зонная теория твердых тел Для того, чтобы
- 9. Зонная теория твердых тел
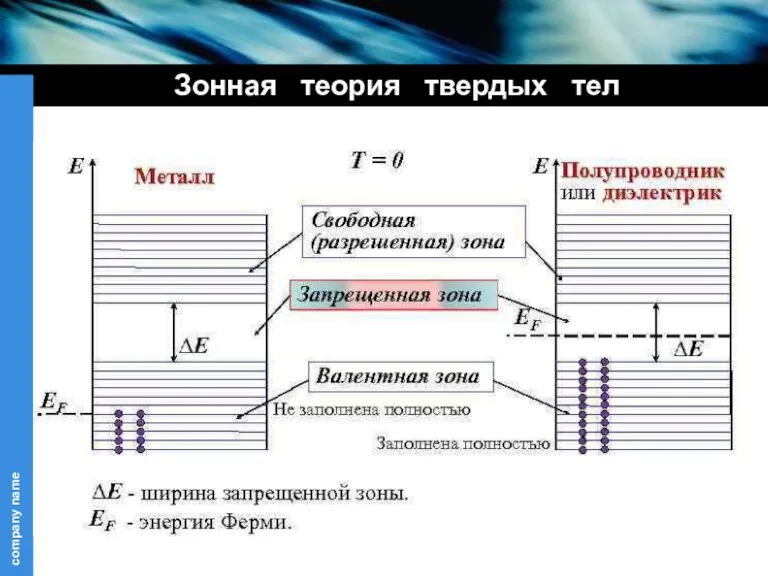
- 10. Зонная теория твердых тел Металлы Зона проводимости образована не полностью заполненной валентной зоной. Например: K, Na,
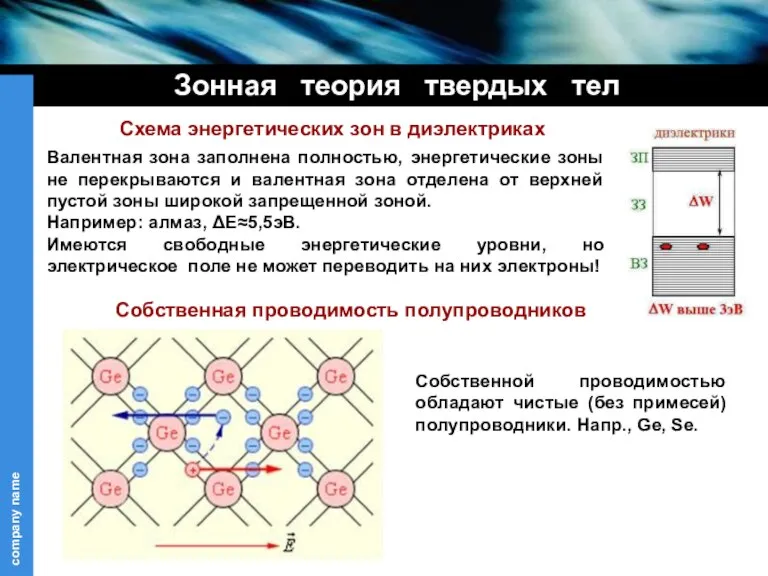
- 11. Зонная теория твердых тел Схема энергетических зон в диэлектриках Валентная зона заполнена полностью, энергетические зоны не
- 12. Зонная теория твердых тел Полупроводники имеют сравнительно узкую запрещенную зону, отделяющую заполненную валентную зону от верхней
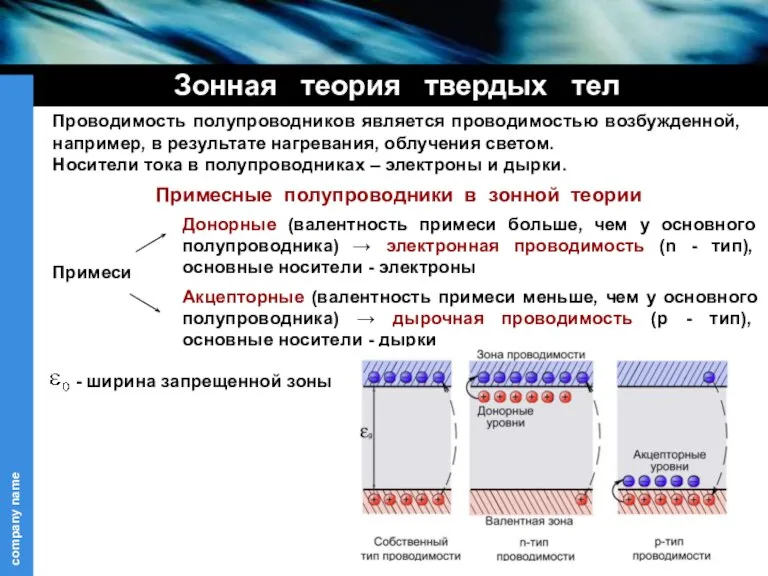
- 13. Зонная теория твердых тел Проводимость полупроводников является проводимостью возбужденной, например, в результате нагревания, облучения светом. Носители
- 14. Примесные полупроводники Донорные примеси (элементы V группы As, Sb, и т.д.) Донор – это примесный атом
- 15. Акцепторные примеси Акцепторные примеси (элементы III группы B, Al, и т.д.) Акцептор – это примесный атом,
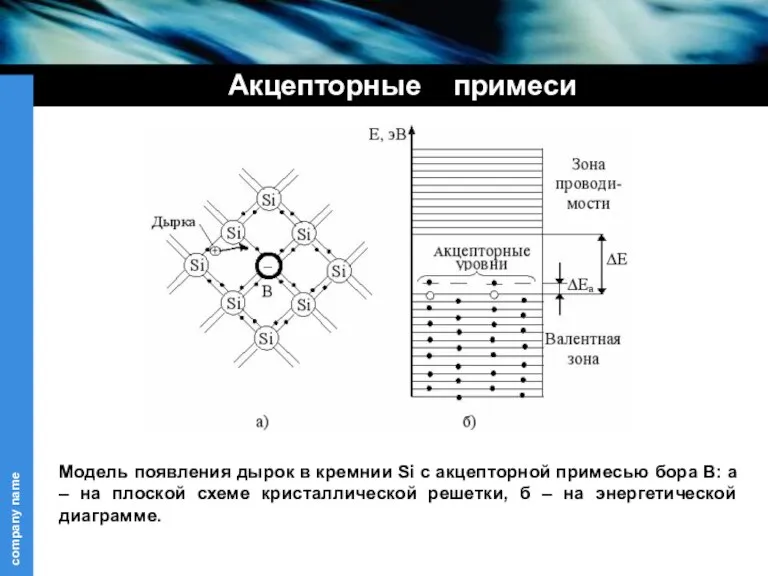
- 16. Акцепторные примеси Модель появления дырок в кремнии Si с акцепторной примесью бора B: а – на
- 17. Уровень Ферми В собственном полупроводнике уровень Ферми находится в середине запрещенной зоны. - уровень Ферми в
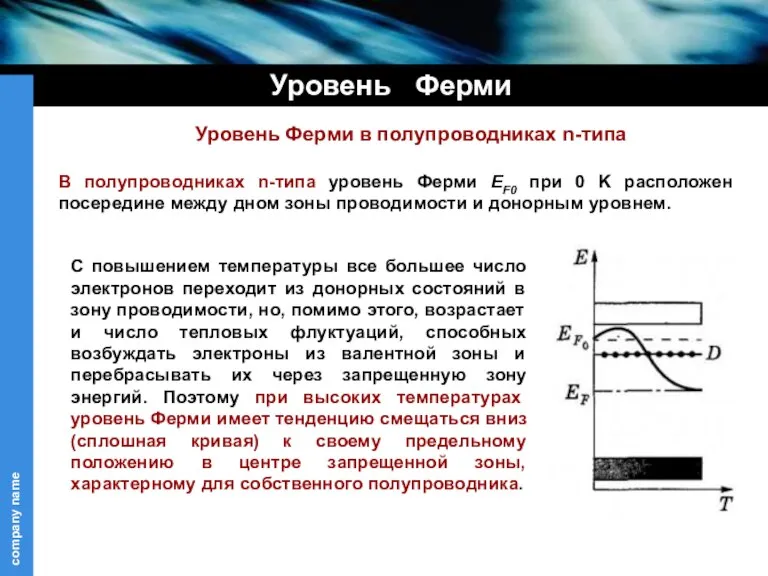
- 18. Уровень Ферми В полупроводниках n-типа уровень Ферми EF0 при 0 K расположен посередине между дном зоны
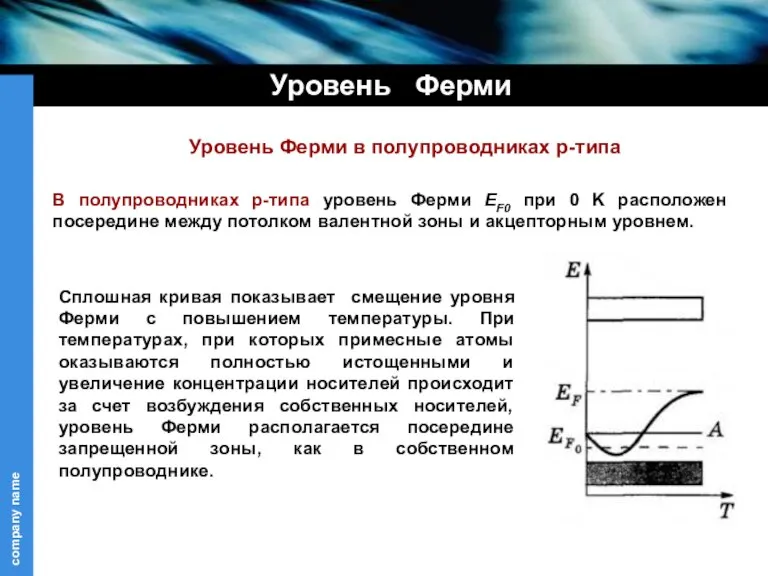
- 19. Уровень Ферми В полупроводниках p-типа уровень Ферми EF0 при 0 K расположен посередине между потолком валентной
- 20. Уровень Ферми Проводимость примесного полупроводника определяется концентрацией носителей и их подвижностью. Зависимость проводимости примесного полупроводника от
- 21. При комнатной температуре практически все свободные электроны находятся внутри металла. Их удерживает электрическое поле положительных ионов.
- 22. электростатическое притяжение между положительно заряженным металлом и отрицательно заряженным электроном, потенциальный барьер между положительно заряженным металлом
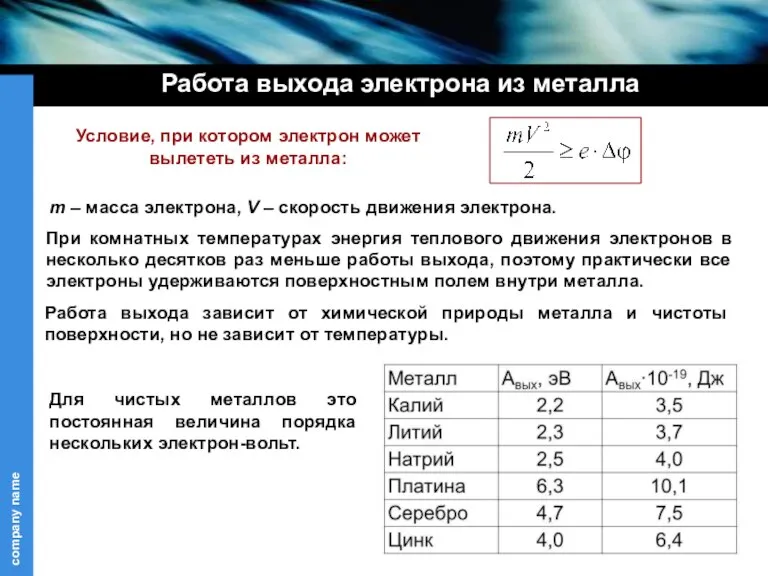
- 23. m – масса электрона, V – скорость движения электрона. При комнатных температурах энергия теплового движения электронов
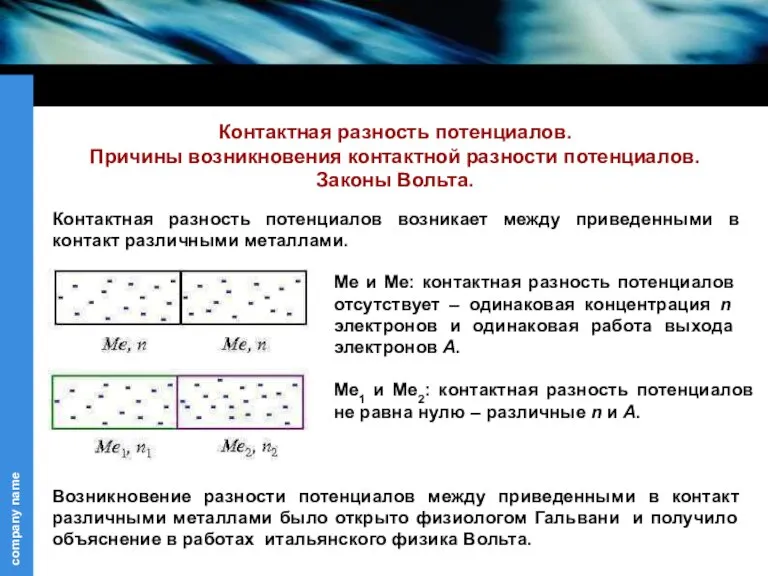
- 24. Контактная разность потенциалов возникает между приведенными в контакт различными металлами. Контактная разность потенциалов. Причины возникновения контактной
- 25. Луиджи Гальвани (1737-1798 г.) Итальянский врач, физиолог и физик. Один из основоположников учения об электричестве, обнаруживший
- 26. 1. При соединении двух проводников, изготовленных из различных металлов, между ними возникает контактная разность потенциалов, которая
- 27. Контактная разность потенциалов Возникающая разность потенциалов Δφ’ создает электрическое поле, которое затрудняет дальнейший переход электронов из
- 28. Контактная разность потенциалов Под действием перепада давления электроны будут переходить из первого металла во второй. Процесс
- 29. 2. Разность потенциалов между концами цепи, состоящей из последовательно соединенных проводников, находящихся при одинаковой температуре, не
- 30. Законы Вольта Термоэлектрический эффект основан на зависимости контактной разности потенциалов от температуры и заключается в следующем:
- 31. Эффект Зеебека В результате в цепи появляется ЭДС, называемая термоэлектродвижущей силой. Используя формулу для контактной разности
- 32. Законы Вольта Для поддержания постоянного тока в цепи необходимо поддерживать постоянную разность температур. Замкнутая цепь проводников,
- 34. Скачать презентацию






















 Классификация химических, физических и механических свойств порошка
Классификация химических, физических и механических свойств порошка Электроннолучевая обработка
Электроннолучевая обработка Источники света. Распространение света
Источники света. Распространение света Электромагнитные явления
Электромагнитные явления Измерение мощности и работы тока в электрической лампе. Лабораторная работа
Измерение мощности и работы тока в электрической лампе. Лабораторная работа Ядерные реакции
Ядерные реакции Расчет пути и времени движения
Расчет пути и времени движения Понятие давления
Понятие давления Достижения в науке и технике в строительстве паровых тубин
Достижения в науке и технике в строительстве паровых тубин Классификация тепловых двигателей
Классификация тепловых двигателей otkritie_elektromagnitnoi_indukcii
otkritie_elektromagnitnoi_indukcii Швейная машина. 5 класс
Швейная машина. 5 класс Свет
Свет В.А. Грибов. Я сдам ЕГЭ. Физика
В.А. Грибов. Я сдам ЕГЭ. Физика Волшебный магнит
Волшебный магнит Электрооборудование автомобиля. Система зажигания
Электрооборудование автомобиля. Система зажигания Динамика. Законы Ньютона
Динамика. Законы Ньютона Вынужденные колебания
Вынужденные колебания Молекула, наименьшая частица вещества
Молекула, наименьшая частица вещества Презентация на тему Законы геометрической оптики
Презентация на тему Законы геометрической оптики  Использование элементов проблемного обучения на уроках физики
Использование элементов проблемного обучения на уроках физики Теоретические основы электротехники. Теория электромагнитного поля. Лекция 10
Теоретические основы электротехники. Теория электромагнитного поля. Лекция 10 Линзы. Построение изображения, даваемое тонкой линзой
Линзы. Построение изображения, даваемое тонкой линзой Магнитное поле тока. Вектор магнитной индукции
Магнитное поле тока. Вектор магнитной индукции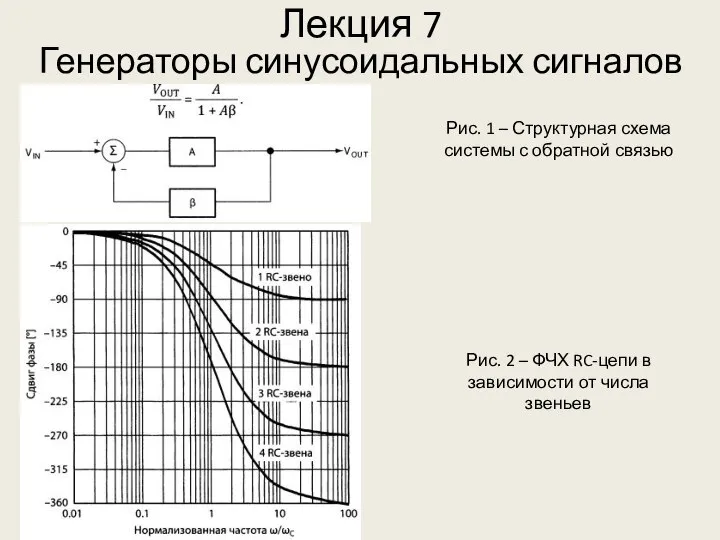 Генераторы синусоидальных сигналов. (Лекция 7)
Генераторы синусоидальных сигналов. (Лекция 7) Формула Планка
Формула Планка Характеристика и свойства электромагнитных волн
Характеристика и свойства электромагнитных волн Электромагнитные явления
Электромагнитные явления