Физические основы акустических методов исследования

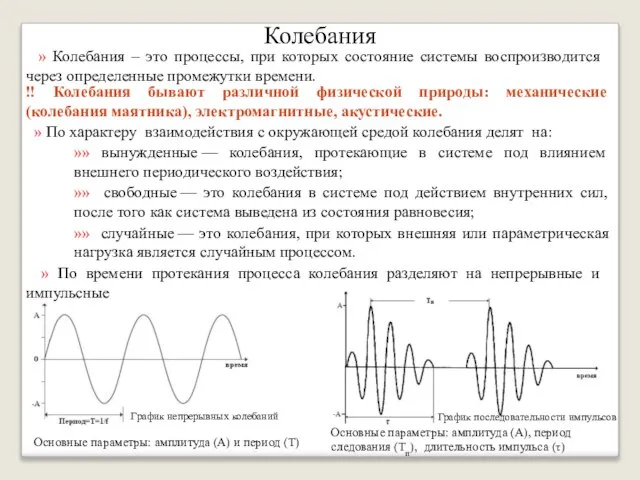
Колебания
» Колебания – это процессы, при которых состояние системы воспроизводится через определенные промежутки времени.
‼ Колебания бывают различной физической природы: механические (колебания маятника), электромагнитные, акустические.
График непрерывных колебаний
» По характеру взаимодействия с окружающей средой колебания делят на:
»» вынужденные — колебания, протекающие в системе под влиянием внешнего периодического воздействия;
»» свободные — это колебания в системе под действием внутренних сил, после того как система выведена из состояния равновесия;
» По времени протекания процесса колебания разделяют на непрерывные и импульсные
График последовательности импульсов
Основные параметры: амплитуда (А) и период (Т)
Основные параметры: амплитуда (А), период следования (Тп), длительность импульса (τ)
»» случайные — это колебания, при которых внешняя или параметрическая нагрузка является случайным процессом.

Диапазоны частот упругих колебаний
» В зависимости от частоты упругие колебания и волны подразделяются на:
»» инфразвуковые (частота колебаний ниже 20 Гц)
»» звук (частота колебаний от 20 Гц до 2*104 Гц)
»» ультразвук (частота колебаний от 2*104 Гц до 1*109 Гц)
»» гиперзвук (частота колебаний выше 1*109 Гц)
» В практике УЗК на железнодорожном транспорте наиболее употребим диапазон частот 0,4-5,0 МГц
» Для справки:
»» 1 Гц – один Герц (одно колебание в секунду);
»» 1000 Гц = 1 кГц – один килогерц;
»» 1 000 000 Гц = 1000 кГц = 1 МГц – один мегагерц;
»» 1 000 000 000 Гц = 1000 МГц = 1 ГГц – один гигагерц;

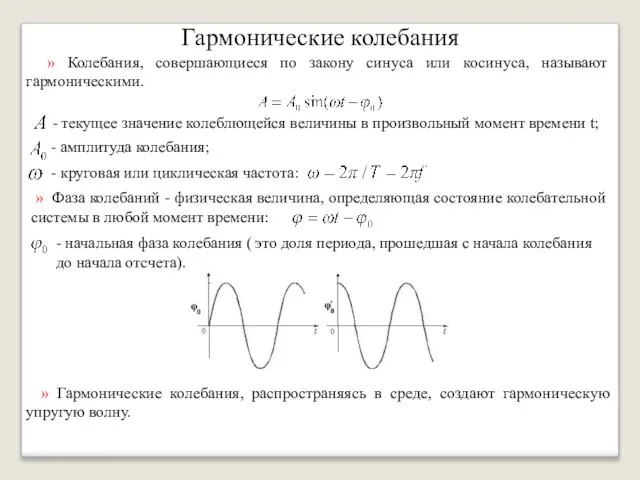
Гармонические колебания
» Колебания, совершающиеся по закону синуса или косинуса, называют гармоническими. - текущее значение колеблющейся величины в произвольный момент времени t;
- амплитуда колебания;
- круговая или циклическая частота:
- начальная фаза колебания ( это доля периода, прошедшая с начала колебания до начала отсчета).
» Фаза колебаний - физическая величина, определяющая состояние колебательной системы в любой момент времени:
» Гармонические колебания, распространяясь в среде, создают гармоническую упругую волну.

Таблица отношений амплитуд и соответствующие значения в децибелах
дБ

Упругие колебания и волны
» Упругость – это свойство твердых тел восстанавливать свою форму и объем после прекращения действия внешних сил. Среду обладающей упругостью называют упругой средой.
» Упругие колебания – это колебания упругой среды или ее частиц, возникающие под действием механического возмущения.
» Упругие или акустические волны – механические возмущения, распространяющиеся в упругой среде.
или
» Упругие или акустические волны – это процесс распространения упругих колебаний (механических возмущений - деформаций) в материальной среде (твердой, жидкой и газообразной)
Различают:
»» в твердых, жидких и газообразных средах существует упругость объема (эти среды восстанавливают свой объем после сжатия или растяжения)
»» в твердых средах помимо упругости объема существует также упругость формы (свойство восстанавливать свою форму после сжатия или растяжения)
‼ Упругие волны осуществляют перенос энергии без переноса вещества

Упругие модули среды
» Изотропная среда – это среда свойства которой одинаковы по всем направлениям.
» Анизотропная среда – это среда свойства которой отличаются в разных направлениях.
» Свойства упругой среды характеризуются её упругими модулями: модулем Юнга E и коэффициентом Пуассона ν.
»» Модуль Юнга - коэффициент, характеризующий сопротивление материала растяжению/сжатию при упругой деформации и равный нормальному напряжению, при котором линейный размер тела изменится в два раза. Модуль Юнга для стали 210 ГПа, а для алюминия 70 ГПа.
»» Коэффициент Пуассона показывает, во сколько раз поперечная деформация деформируемого тела больше продольной деформации при растяжении или сжатии тела. Для абсолютно хрупкого материала коэффициент Пуассона равен 0, для абсолютно упругого — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он примерно равен 0,5.
» Модуль сдвига G - описывает отклик материала на сдвиговую нагрузку. Модуль сдвига равен касательному напряжению, которое возникло бы в образце при относительном сдвиге, равном единице. Модуль сдвига выражается через модуль Юнга и коэффициент Пуассона.

Закон Гука
» Закон Гука: напряжение упруго деформированного тела прямо пропорционально его относительной деформации.
» Мерой деформации служит относительная деформация, равная отношению абсолютной деформации △l к первоначальному значению величины l, характеризующей форму или размеры тела.
» Kl – модуль упругости, числено равный напряжению, которое возникает при относительной деформации равной единице.

Основные параметры ультразвуковой волны
» Упругие волны характеризуются следующими параметрами:
»» длиной волны – λ, [м], [мм]
»» частотой– f, [Гц], [МГц]
»» скоростью распространения – с, [м/с], [мм/мкс]
» Длина волны – минимальное расстояние между двумя точками колеблющимися в одной фазе (или расстояние, на которое распространяется процесс за время, равное одному периоду T )
» Частота – количество колебаний материальной точки, измеряемое в герцах
» Скорость распространения – это скорость, с которой колебания передаются от одной материальной частицы среды к другой (или скорость распространения одинакового фазового состояния колебаний)
Три основных параметра ультразвуковой волны связаны между собой формулой:
‼ Длину волны в любой среде можно изменить путем изменения частоты колебаний
‼ Все параметры колебаний относятся и к волнам

Волновой фронт
» Совокупность точек, колеблющихся в одинаковой фазе, образуют волновой фронт. » Распространение волны происходит в направлении нормали к волновому фронту в каждой точке. Существует три основных вида волнового фронта: плоский, цилиндрический и сферический
» Плоские волны образуются на малых расстояниях от плоского излучателя. Цилиндрические волны создает излучатель, удлиненный в одном направлении. Сферические волны получаются, если волна прошла расстояние, много больше размера излучателя.

Типы поляризаций упругих волн
» Поляризацией волны называется траектория и направление движения частиц упругой среды по отношению к направлению распространения.
» В общем случае волна имеет эллиптическую поляризацию (т.е. частицы совершают движение по эллипсу).
» В частном случае эллипс вырождается в линию . Говорят, что такие волны имеют линейную поляризацию, они относятся к объемным волнам.

Типы ультразвуковых волн
» В зависимости от упругих свойств среды в ней могут возникать ультразвуковые волны различных типов, отличающиеся направлением смещения колеблющихся частиц и скоростью распространения:
»» продольные волны или волны растяжения-сжатия (L-волны): существуют во всех средах;
»» поперечные или сдвиговые волны (T-волны): существуют в твердых средах, обладают упругостью формы;
‼ обобщенное название продольных и поперечных волн – объемные волны
»» поверхностные волны (R-волны или волны Рэлея, распространяются вдоль поверхности твердого тела);
»» нормальные волны ( например волны Лэмба, распространяющиеся в пластинах или волны Похгаммера, распространяющиеся в стержнях, прутках).
‼ В ультразвуковой дефектоскопии на железной дороге чаще всего используют продольные, поперечные и поверхностные волны.
»» головные (подповерхностные) волны – это волны, распространяющиеся вблизи поверхности твердого тела;

Продольные волны
» Продольной называется такая волна, у которой направление движение частиц происходит в том же направлении, в котором распространяется волна.
» При распространении продольной волны в среде образуются области растяжения и сжатия.
» Скорость продольной волны можно рассчитать по известным значениям плотности ρ, модуля Юнга E и коэффициента Пуассона ν.
» Для некоторых материалов:
в стали – 5900 м/с;
в воде – 1450 м/с;
в органическом стекле – 2670 м/с;
в воздухе (при температуре 0ºС) – 331 м/с;

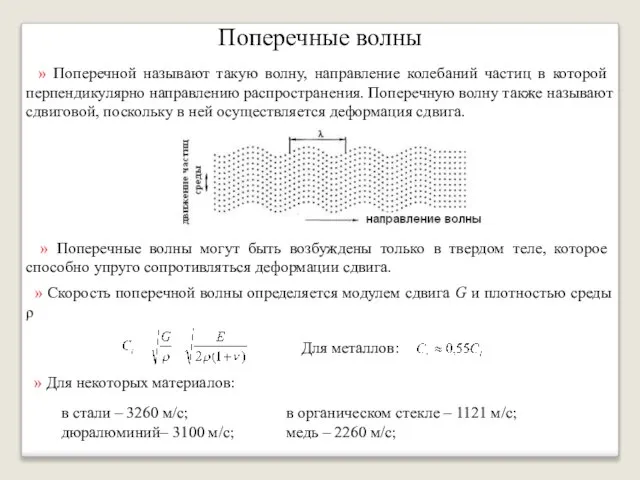
Поперечные волны
» Поперечной называют такую волну, направление колебаний частиц в которой перпендикулярно направлению распространения. Поперечную волну также называют сдвиговой, поскольку в ней осуществляется деформация сдвига.
» Поперечные волны могут быть возбуждены только в твердом теле, которое способно упруго сопротивляться деформации сдвига.
» Для некоторых материалов:
в стали – 3260 м/с;
дюралюминий– 3100 м/с;
в органическом стекле – 1121 м/с;
медь – 2260 м/с;
» Скорость поперечной волны определяется модулем сдвига G и плотностью среды ρ
Для металлов:

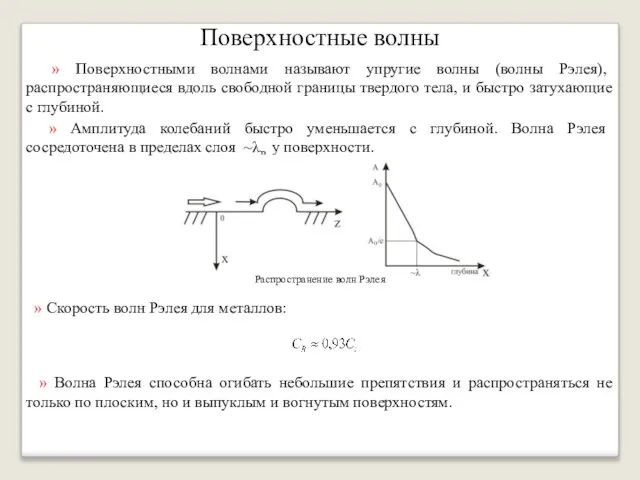
Поверхностные волны
» Поверхностными волнами называют упругие волны (волны Рэлея), распространяющиеся вдоль свободной границы твердого тела, и быстро затухающие с глубиной.
» Амплитуда колебаний быстро уменьшается с глубиной. Волна Рэлея сосредоточена в пределах слоя ~λR у поверхности.
Распространение волн Рэлея
» Скорость волн Рэлея для металлов:
» Волна Рэлея способна огибать небольшие препятствия и распространяться не только по плоским, но и выпуклым и вогнутым поверхностям.

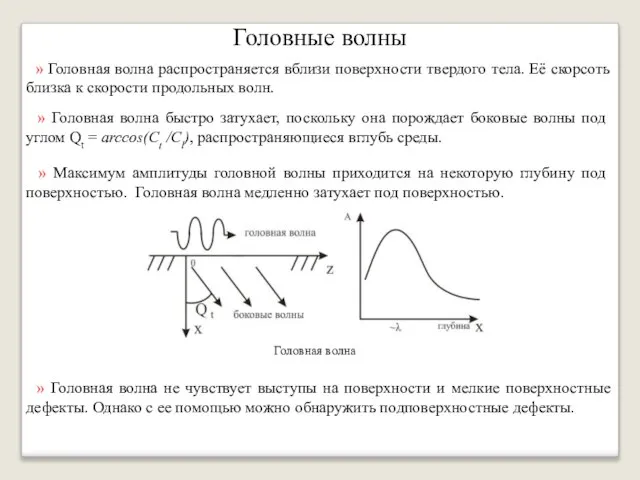
Головные волны
» Головная волна распространяется вблизи поверхности твердого тела. Её скорсоть близка к скорости продольных волн.
» Головная волна быстро затухает, поскольку она порождает боковые волны под углом Qt = arccos(Сt /Cl), распространяющиеся вглубь среды.
» Максимум амплитуды головной волны приходится на некоторую глубину под поверхностью. Головная волна медленно затухает под поверхностью.
» Головная волна не чувствует выступы на поверхности и мелкие поверхностные дефекты. Однако с ее помощью можно обнаружить подповерхностные дефекты.
Головная волна

Волны Лэмба
» Волнами в пластинах называют упругие волны, распространяющиеся в твердой пластине (слое) со свободными или слабо нагруженными гранями.
» Существует несколько типов волн Лэмба. Моды, колебания которых симметричны относительно оси пластины, называют симметричными (обозначение sн). Моды, колебания которых асимметричны относительно оси, называют асимметричными (обозначение aн).
симметричная мода
асимметричная мода
» В волнах Лэмба скорость распространения фазы волны вдоль пластины (фазовая скорость) не равна групповой скорости, с которой переносится энергия. Фазовая скорость волны Лэмба зависит от частоты ультразвуковой волны и от толщины пластины.
‼ Зависимость скорости распространения волны от частоты называется дисперсией. Волны Лэмба обладают дисперсией.

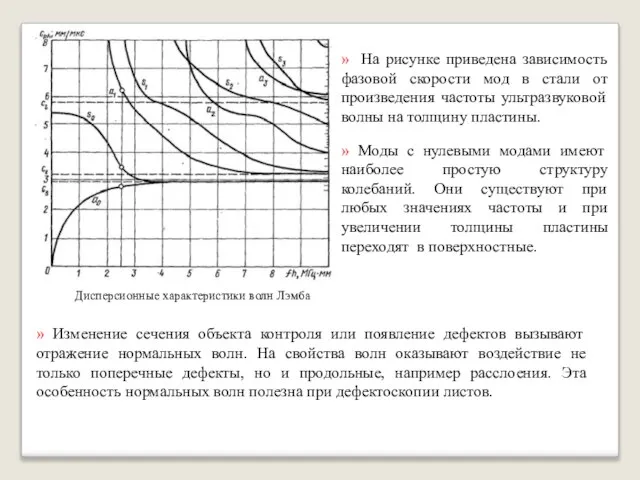
» На рисунке приведена зависимость фазовой скорости мод в стали от произведения частоты ультразвуковой волны на толщину пластины.
» Моды с нулевыми модами имеют наиболее простую структуру колебаний. Они существуют при любых значениях частоты и при увеличении толщины пластины переходят в поверхностные.
Дисперсионные характеристики волн Лэмба
» Изменение сечения объекта контроля или появление дефектов вызывают отражение нормальных волн. На свойства волн оказывают воздействие не только поперечные дефекты, но и продольные, например расслоения. Эта особенность нормальных волн полезна при дефектоскопии листов.

Волны в стержнях
» В стержнях, как и в пластинах, существуют нормальные волны. Волны в круглых стержнях называют волнами Похгаммера.
» Различают симметричные и несимметричные моды. Наиболее применяемые волны в стержнях:
»» Волны изгиба
»» Волны расширения-сжатия
»» Крутильные волны. Они характеризуются поворотом частиц вокруг оси стержня.
‼ Волны в стержнях обладают дисперсией скорости.
» Нормальные моды в стержнях возбуждают наклонным падением продольной волны из внешней среды, а крутильную волну – электромагнитно-акустическими преобразователями. Волны в стержнях применяют для контроля прутков и проволок.

Волновое сопротивление
» Волновое сопротивление представляет собой характеристический импеданс среды и характеризует степень её жесткости, т.е. способность среды сопротивляться образованию деформаций.
» Волновое сопротивление — важнейшая характеристика среды, определяющая условия отражения и преломления волн на её границе.
ρ – плотность среды, с –скорость волны заданного типа.
» Пример расчета:
Для стали ρ =7800 кг/м3 ; сl =5900 м/с ; сt =3200 м/с
Для продольных волн:
Для поперечных волн:

Ослабление волн при распространении. Коэффициент затухания
» Основные причины ослабления волн: расхождение фронта волны и затухание.
» Ослабление из-за расхождения происходит вследствие того, что с пройденным расстоянием фронт волны расширяется, следовательно, происходит перераспределение энергии в пространстве, охваченном волновым фронтом.
» Уменьшение амплитуды сферических волн пропорционально 1/R, где R – пройденное расстояние, цилиндрических – 1/√R.
В плоских волнах расхождения нет.
» Ослабление волн из-за затухания пропорционально e-δ*R , где e≈2,73, δ – коэффициент затухания. Коэффициент затухания складывается из их коэффициентов поглощения δп и рассеяния δр.
» При поглощении звуковая энергия переходит в другие виды, в первую очередь в тепловую. Рассеяние связано с процессами преломления, отражения волн на границах кристаллов, зерен или включений в неоднородных материалах, а также огибанием волнами этих внутренних неоднородностей.
» Коэффициенты δ, δп , δр измеряются в [1/м и 1/см]. В технике часто используют единицы [дБ/м и дБ/см]

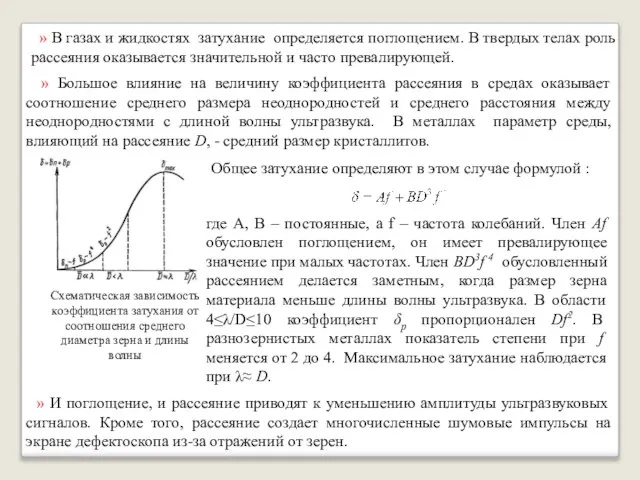
» Большое влияние на величину коэффициента рассеяния в средах оказывает соотношение среднего размера неоднородностей и среднего расстояния между неоднородностями с длиной волны ультразвука. В металлах параметр среды, влияющий на рассеяние D, - средний размер кристаллитов.
» В газах и жидкостях затухание определяется поглощением. В твердых телах роль рассеяния оказывается значительной и часто превалирующей.
Схематическая зависимость коэффициента затухания от соотношения среднего диаметра зерна и длины волны
Общее затухание определяют в этом случае формулой :
где A, B – постоянные, а f – частота колебаний. Член Af обусловлен поглощением, он имеет превалирующее значение при малых частотах. Член BD3f 4 обусловленный рассеянием делается заметным, когда размер зерна материала меньше длины волны ультразвука. В области 4≤λ/D≤10 коэффициент δр пропорционален Df2. В разнозернистых металлах показатель степени при f меняется от 2 до 4. Максимальное затухание наблюдается при λ≈ D.
» И поглощение, и рассеяние приводят к уменьшению амплитуды ультразвуковых сигналов. Кроме того, рассеяние создает многочисленные шумовые импульсы на экране дефектоскопа из-за отражений от зерен.

Отражение и прохождение волн на границе сред
» При падении упругой волны на границу раздела двух сред происходит несколько явлений: отражение, преломление и трансформация.
»» Отражением называется изменение направления распространения волн на границе раздела, при котором волна не переходит в другую среду.
»» Преломлением называется изменение направления и скорости волны на границе раздела, при котором волна переходит в другую среду.
»» Трансформацией называют преобразование типа или поляризации волн, происходящее на границе раздела сред.
» В наиболее общем случае границы двух твердых сред возникает две отраженные (продольная и поперечная), две преломленные волны.
‼ Для падающей, отраженных и преломленных волн отношение синуса угла (между направлением распространения и нормалью к поверхности раздела) к скорости волны есть величина постоянная.
Закон отражения и преломления для двух сред или закон Снеллиуса

» n – коэффициент преломления
» Чем больше скорость прошедшей (преломленной) волны, тем больше угол.
а)
б)
» В случае а) преломленная волна существует всегда, при значения угла падения от 0º до 90º .
» В случае б) α>β. При увеличении β обязательно настанет момент, когда преломленная волна пойдет параллельно поверхности. Говорят, что в этом случае волна падает под критическим углом.
‼ В ультразвуковом контроле вводятся три критических угла.
» Угол падения, при котором преломленная продольная волна выходит на поверхность раздела сред, называется первым критическим углом β1. Преломленная волна при этом превращается в головную. При значениях угла падения, превышающих первый критический, во второй среде продольная волна отсутствует.

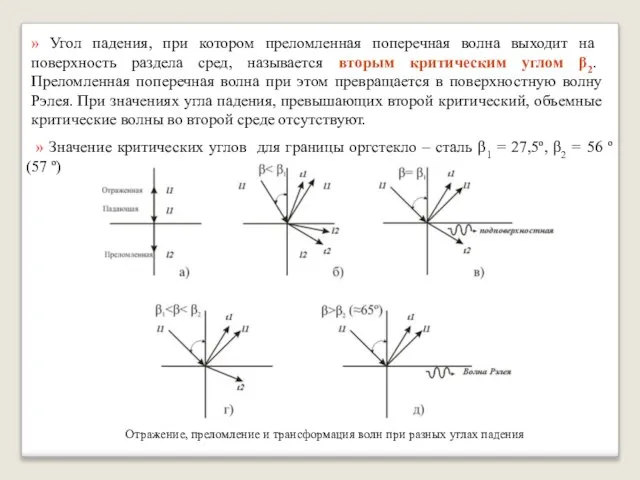
» Угол падения, при котором преломленная поперечная волна выходит на поверхность раздела сред, называется вторым критическим углом β2. Преломленная поперечная волна при этом превращается в поверхностную волну Рэлея. При значениях угла падения, превышающих второй критический, объемные критические волны во второй среде отсутствуют.
» Значение критических углов для границы оргстекло – сталь β1 = 27,5º, β2 = 56 º (57 º)
Отражение, преломление и трансформация волн при разных углах падения

» В случае нормального падения отсутствует преломление лучей. Падающая, отраженная и преломленная (прошедшая) волны направлены по нормали к поверхности контроля. Трансформации волн тоже нет.
» При значении угла падения, меньшим первого критического, во второй среде есть две преломленные волны, продольная и поперечная.
» В случае падения под первым критическим углом вместо вышедшей на поверхность продольной преломленной волны образуется головная.
» Если β1 <β< β2 , то во второй среде есть только поперечная волна.
» При β > β2 , объемных волн во второй среде нет, а вдоль границы раздела бежит поверхностная волна.
» Угол падения поперечной волны, при котором отраженная продольная волна выходит на поверхность, называется третьим критическим углом β3 . Для стали этот угол равен 33º. В этом случая продольная волна сливается с поверхностью и становится неоднородной.
‼ Для практики важны случаи, когда на границу твердого тела (объекта контроля) падает из жидкости продольная волна (иммерсионный контроль) или она падает из другого твердого тела (призмы преобразователя), отделенного от объекта контроля тонким слоем жидкости

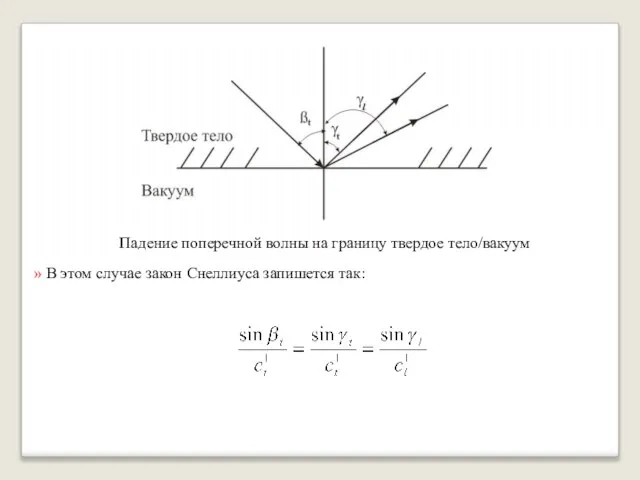
Падение поперечной волны на границу твердое тело/вакуум
» В этом случае закон Снеллиуса запишется так:

Отражение и прохождение волн на границе сред
» Падение волны на границу раздела называется нормальным, если угол падения равен нулю. В этом случае не происходит видимого преломления луча. Углы преломления и отражения равны нулю. Трансформации волн при нормальном падении не происходит.
» Для количественной характеристики степени отражения и преломления волн вводят коэффициенты отражения и прохождения.
» При нормальном падении волны коэффициент отражения по энергии:
где z - характеристический импеданс
» Коэффициент прохождения по энергии связан с коэффициентом отражения по энергии соотношением, вытекающим из закона сохранения энергии:
» Например при нормальном падении продольной волны на границу сталь/вода коэффициент отражения приблизительно равен 0,9, следовательно коэффициент прохождения равен 0,1.
‼ Чем больше отличаются характеристические импедансы сред, тем большая часть энергии отражается, и меньшая проходит во вторую среду.

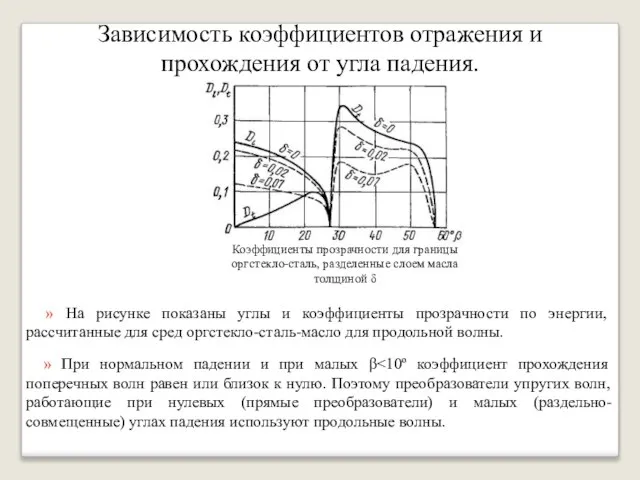
Зависимость коэффициентов отражения и прохождения от угла падения.
» На рисунке показаны углы и коэффициенты прозрачности по энергии, рассчитанные для сред оргстекло-сталь-масло для продольной волны.
Коэффициенты прозрачности для границы оргстекло-сталь, разделенные слоем масла толщиной δ
» При нормальном падении и при малых β<10º коэффициент прохождения поперечных волн равен или близок к нулю. Поэтому преобразователи упругих волн, работающие при нулевых (прямые преобразователи) и малых (раздельно-совмещенные) углах падения используют продольные волны.

» При значении угла падения, равном первому критическому, коэффициенты прохождения близки к нулю. Значительная часть энергии излучения переносится подповерхностной волной. Падение волны под первым критическим углом используют для возбуждения подповерхностных волн.
» При углах падения, больших первого критического, продольной преломленной волны нет.
» В интервале углов β1 <β< β2 во второй среде (стали) распространяется только поперечная волна. Этот интервал углов падения, приблизительно от 30º до 55º, используется в преобразователях поперечных волн. Пластина преобразователя возбуждает в призме наклонного преобразователя продольную волну. После преломления и трансформации в объекте контроля распространяется поперечная волна.
» Поперечная волна исчезает при величине угла падения β> β2 . Если угол падения равен или немного превышает второй критический, то возбуждается и распространяется вдоль поверхности поверхностная волна. Углы падения 60º - 65º используются для возбуждения поверхностной волны.

Отражение от двугранного угла
» Отраженная волна того же типа что и падающая имеет некоторое смещение по расстоянию
» Если на двугранный угол падает сферическая волна от источника в точке О, то можно представить, что отраженные лучи излучаются мнимыми источником, расположенным в точке О1 . При этом нижние лучи становятся верхними, и наоборот.
» Из-за трансформации волн амплитуда отраженной волны зависит от угла падения, так как энергия падающей волны частично превращается в энергию волны другого типа.
» Для поперечной волны коэффициент отражения будет равен единице, если углы падения на обе грани (это углы α, 90º-α) больше третьего критического. Это интервал углов от 33,5º до 56,5º
» Зависимость коэффициента отражения от угла падения волны на двугранный угол используется для настройки чувствительности дефектоскопа при контроле наклонным преобразователем.

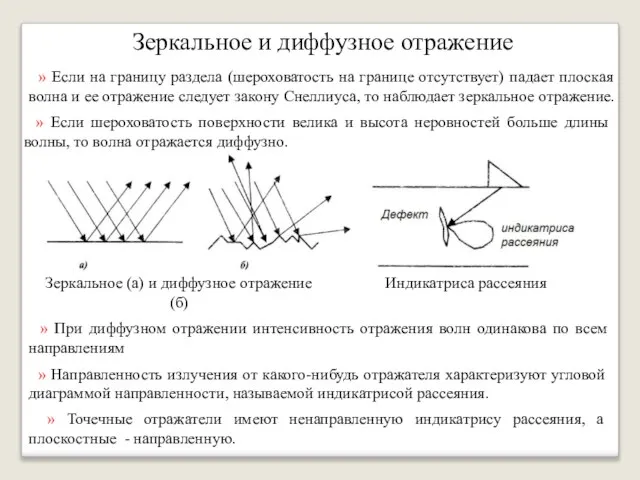
Зеркальное и диффузное отражение
» Если на границу раздела (шероховатость на границе отсутствует) падает плоская волна и ее отражение следует закону Снеллиуса, то наблюдает зеркальное отражение.
» Если шероховатость поверхности велика и высота неровностей больше длины волны, то волна отражается диффузно.
Зеркальное (а) и диффузное отражение (б)
» При диффузном отражении интенсивность отражения волн одинакова по всем направлениям
Индикатриса рассеяния
» Направленность излучения от какого-нибудь отражателя характеризуют угловой диаграммой направленности, называемой индикатрисой рассеяния.
» Точечные отражатели имеют ненаправленную индикатрису рассеяния, а плоскостные - направленную.

Интерференция и дифракция ультразвуковых волн
» Интерференция - это сложение в пространстве двух или нескольких ультразвуковых волн, при котором в разных точках получается усиление или ослабление амплитуды результирующей волны.
Примеры интерференционных картин
» Дифракция – это явление огибания волной препятствия, находящегося на пути его распространения.
Дифракция волн. Частичное огибание пучком препятствия
Дифракция проявляется тем сильнее, чем меньше размеры препятствий, например отражателей. Если размеры отражателя существенно меньше длины волны, то волна огибает отражатель и сколь-нибудь существенного отражения не возникает.

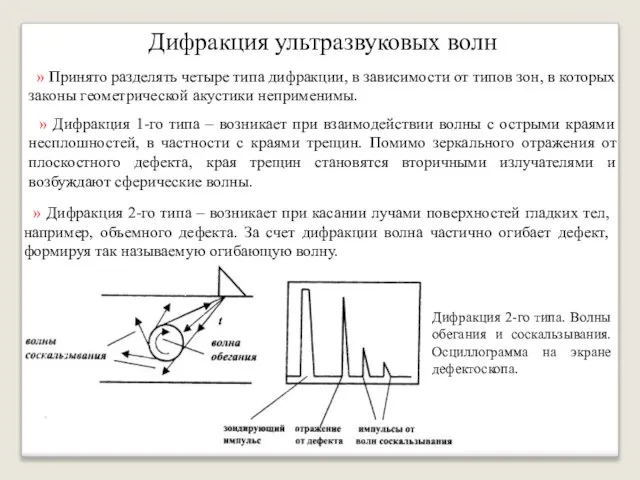
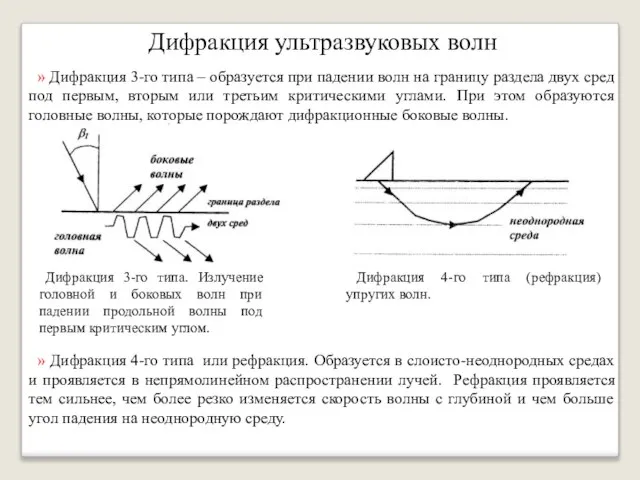
Дифракция ультразвуковых волн
» Принято разделять четыре типа дифракции, в зависимости от типов зон, в которых законы геометрической акустики неприменимы.
» Дифракция 1-го типа – возникает при взаимодействии волны с острыми краями несплошностей, в частности с краями трещин. Помимо зеркального отражения от плоскостного дефекта, края трещин становятся вторичными излучателями и возбуждают сферические волны.
» Дифракция 2-го типа – возникает при касании лучами поверхностей гладких тел, например, объемного дефекта. За счет дифракции волна частично огибает дефект, формируя так называемую огибающую волну.
Дифракция 2-го типа. Волны обегания и соскальзывания. Осциллограмма на экране дефектоскопа.

Дифракция ультразвуковых волн
Дифракция 3-го типа. Излучение головной и боковых волн при падении продольной волны под первым критическим углом.
» Дифракция 4-го типа или рефракция. Образуется в слоисто-неоднородных средах и проявляется в непрямолинейном распространении лучей. Рефракция проявляется тем сильнее, чем более резко изменяется скорость волны с глубиной и чем больше угол падения на неоднородную среду.
» Дифракция 3-го типа – образуется при падении волн на границу раздела двух сред под первым, вторым или третьим критическими углами. При этом образуются головные волны, которые порождают дифракционные боковые волны.
Дифракция 4-го типа (рефракция) упругих волн.

Акустическое поле преобразователя
» Акустическим полем называют область пространства, упругие колебания в точках которого определяются положением относительно объекта, порождающего это поле. Применительно к преобразователю различают: поле излучения, поле приема, поле излучения-приема.
» Поле излучения – определяется давлением которое создается преобразователем и действует на элементарный приемник в произвольной точке пространства.
» Поле приема – определяет амплитуду и фазу колебаний приемного преобразователя при действии на него точечного ненаправленного сферического излучателя, находящегося в некоторой точке пространства.
» Поле излучения-приема определяется сигналом приемного преобразователя, возникающим при отражении излучения этого же преобразователя от точечного отражателя, помещенного в некоторой точке пространства и равномерно рассеивающего падающие волны по всем направлениям.
» Параметры акустического поля зависят от следующих факторов:
- размер преобразователя;
- конструкция преобразователя;
- тип преобразователя;
- рабочая частота колебаний;
- длительность импульса;
- свойства упругой среды, в которой создается поле.

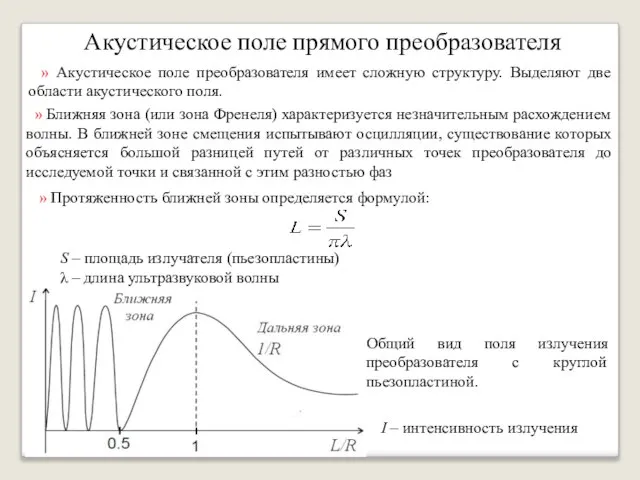
Акустическое поле прямого преобразователя
» Акустическое поле преобразователя имеет сложную структуру. Выделяют две области акустического поля.
» Ближняя зона (или зона Френеля) характеризуется незначительным расхождением волны. В ближней зоне смещения испытывают осцилляции, существование которых объясняется большой разницей путей от различных точек преобразователя до исследуемой точки и связанной с этим разностью фаз
» Протяженность ближней зоны определяется формулой:
S – площадь излучателя (пьезопластины)
λ – длина ультразвуковой волны
Общий вид поля излучения преобразователя с круглой пьезопластиной.
I – интенсивность излучения

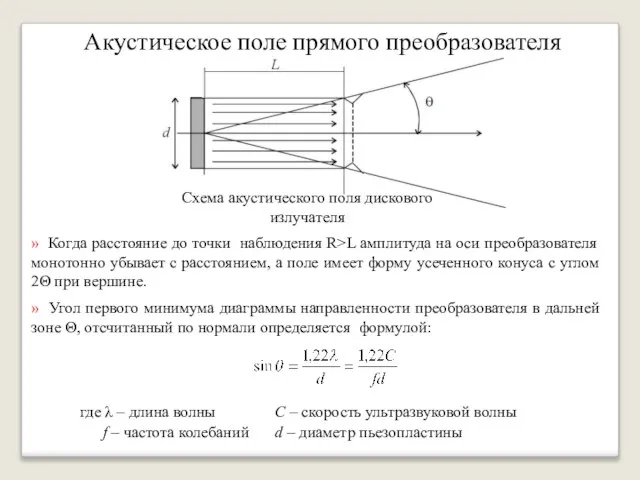
Акустическое поле прямого преобразователя
» Когда расстояние до точки наблюдения R>L амплитуда на оси преобразователя монотонно убывает с расстоянием, а поле имеет форму усеченного конуса с углом 2Θ при вершине.
Схема акустического поля дискового излучателя
» Угол первого минимума диаграммы направленности преобразователя в дальней зоне Θ, отсчитанный по нормали определяется формулой:
где λ – длина волны
f – частота колебаний
С – скорость ультразвуковой волны
d – диаметр пьезопластины

Диаграмма направленности
» Диаграмма направленности – это зависимость амплитуды акустического поля в дальней зоне от угла между акустической осью и направлением конкретного луча.
» Акустическая ось – геометрическая ось, проходящая через точку выхода преобразователя и служащая направлением, от которого отсчитываются угловые координаты, используемые для построения характеристики направленности преобразователя.
» Акустическое поле преобразователя в дальней зоне характеризуется диаграммой направленности.
»» Центральная часть диаграммы, в пределах которой интенсивность изменяется от 1 до нуля, называют основным лепестком. В его пределах заключается 80-85% энергии излучения.
»» Для измерения ширины диаграммы направленности можно использовать СО-2

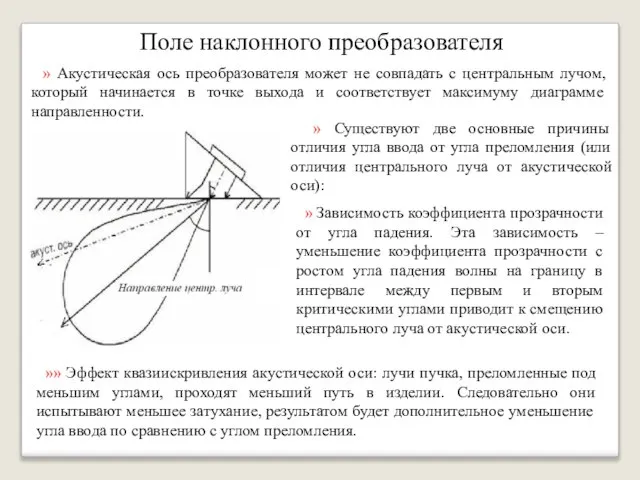
Поле наклонного преобразователя
» В наклонном преобразователе упругие волны сначала распространяются в материале призмы, затем преломляются на границе призма-изделие, трансформируются в поперечные и попадают в объект контроля.
» Призму также называют акустической задержкой, имея в виду то, что благодаря ей прохождение фронта волны задерживается на одинаковые или разные промежутки времени. В последнем (чаще всего применяемом) варианте призма обеспечивает наклонный ввод волн в ОК.
» Акустической осью (ON) преобразователя в ОК называют преломленную акустическую ось пьезопластины.
» Точку преломления O называют точкой выхода.
» Угол преломления центрального луча называется углом ввода.

Поле наклонного преобразователя
» Акустическая ось преобразователя может не совпадать с центральным лучом, который начинается в точке выхода и соответствует максимуму диаграмме направленности.
» Существуют две основные причины отличия угла ввода от угла преломления (или отличия центрального луча от акустической оси):
» Зависимость коэффициента прозрачности от угла падения. Эта зависимость – уменьшение коэффициента прозрачности с ростом угла падения волны на границу в интервале между первым и вторым критическими углами приводит к смещению центрального луча от акустической оси.
»» Эффект квазиискривления акустической оси: лучи пучка, преломленные под меньшим углами, проходят меньший путь в изделии. Следовательно они испытывают меньшее затухание, результатом будет дополнительное уменьшение угла ввода по сравнению с углом преломления.

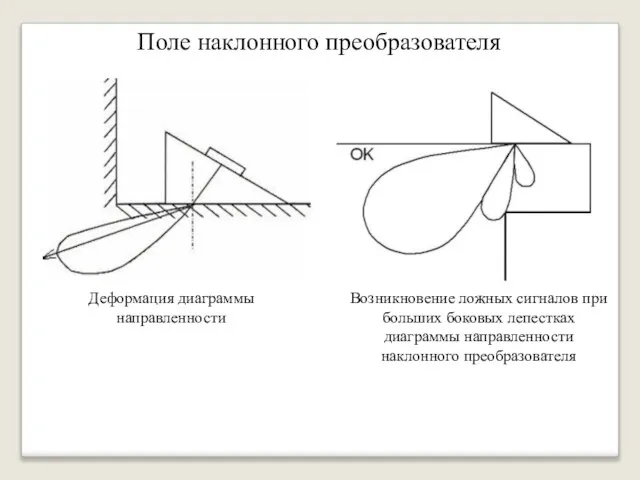
Поле наклонного преобразователя
» При использовании наклонного преобразователя наблюдаются следующие эффекты:
»» Вблизи критических углов наблюдается отклонение от закона Снеллиуса, при этом искажается акустическое поле в объекте контроля. Следствием этого является несовпадение акустической оси и направления центрального луча. Увеличение волнового размера пьезопластины приводит к сужению диаграммы направленности в призме и ослаблению данного эффекта. Увеличение угла призмы приводит к усилению эффекта.
»» В случае, когда боковые лепестки диаграммы направленности достаточно велики, возможно ухудшение чувствительности контроля за счет возникновения дополнительных шумов. Причиной их возникновения является отражение лучей боковых лепестков от различных препятствий в объекте контроля. Как следствие , возникают ложные сигналы, мешающие проведению контроля.
»» Чем больше угол ввода, тем сильнее будут сглаживаться осцилляции амплитуды в ближней зоне. Возникает деформация диаграммы направленности, эффект проявляется тем сильнее, чем меньше произведение радиуса пьезопластины на частоту колебаний.

Деформация диаграммы направленности
Возникновение ложных сигналов при больших боковых лепестках диаграммы направленности наклонного преобразователя
Поле наклонного преобразователя

Мешающие факторы при УЗК контроле
» Помехами называют возмущения, накладывающиеся на принимаемый сигнал и мешающие его приему.
» Шумом называют помехи, случайные по амплитуде, времени прихода, фазе колебаний.
» Помехами при УЗК контроле (преимущественно для эхо-метода) в более узком смысле называют мешающие приему полезных сигналов импульсы, не меняющие своего положения во времени относительно зондирующего импульса при неизменных условиях контроля.
» Различают аддитивные и мультипликативные помехи и шумы. Аддитивные складываются с полезным сигналом, а мультипликативные перемножаются с ним.
» Различают аддитивные и мультипликативные помехи и шумы.
» Аддитивные помехи складываются с полезным сигналом, а мультипликативные перемножаются с ним.
» Примеры источников мультипликативных помех: изменение качества акустического контакта, локальные изменения коэффициентов затухания.
» Далее будут рассмотрены помехи относящиеся к аддитивным.

Внешние шумы
» Импульсы внешних шумов имеют электромагнитную или акустическую природу.
» Источниками электромагнитных помех могут быть:
естественные источники излучения (радиоизлучение Земли и объектов солнечной системы, атмосферные помехи Земли);
искусственные помехи (излучение промышленных установок, бытовых электроприборов, радиолокаторов и т.д.).
» Акустические шумы встречаются гораздо реже, они возникают в результате ударов по ОК. Например, контролю рельсов с помощью вагона-дефектоскопа мешают удары колес о рельсовые стыки.
Шумы электрических цепей
» Обусловлены хаотичным изменением электрических потенциалов и токов на входе приемника – усилителя дефектоскопа. Основной причиной являются тепловые шумы электронных элементов схемы.
Помехи преобразователя
» При контроле по совмещенной схеме контактным способом проявляются в том, что после зондирующего импульса наблюдают отражения ультразвуковых импульсов (иногда многократные) в пьезоэлементе, протекторе, демпфере, призме. При ручном контроле помехи преобразователя отличают от полезного сигнала тем, что не перемещаются по линии развертки во время движения преобразователя по поверхности изделия. По мере удаления во времени от зондирующего импульса эти помехи уменьшаются и исчезают.