Содержание
- 2. Основные особенности и принципы квантовой механики. Соотношение неопределенностей Гейзенберга Понятие о зонной теории твердых тел. Основные
- 3. Основные особенности и принципы квантовой механики. Луи де Бройль 1892 - 1987 Гипотеза де Бройля (1924)
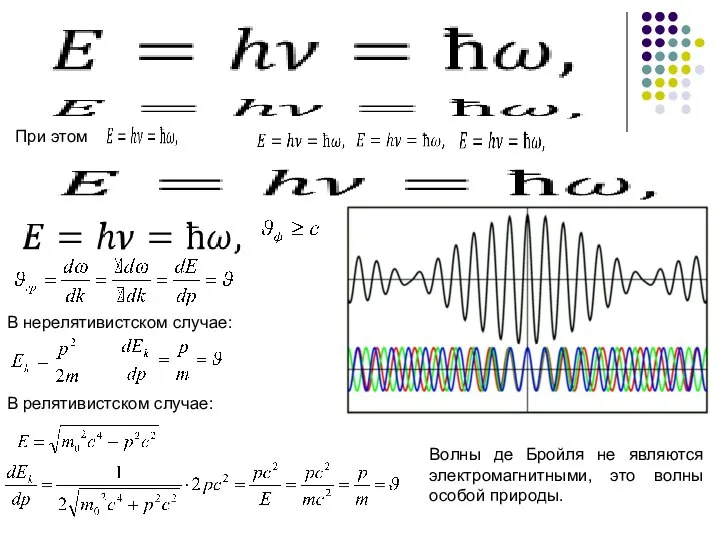
- 4. В нерелятивистском случае: При этом В релятивистском случае: Волны де Бройля не являются электромагнитными, это волны
- 5. . Движение электрона или другой микрочастицы можно представить как суперпозицию плоских гармонических волн, образующих волновой пакет.
- 6. Соотношение неопределенностей Гейзенберга В классической механике состояние материальной точки определяется координатами, энергией, импульсом и т.д. Эти
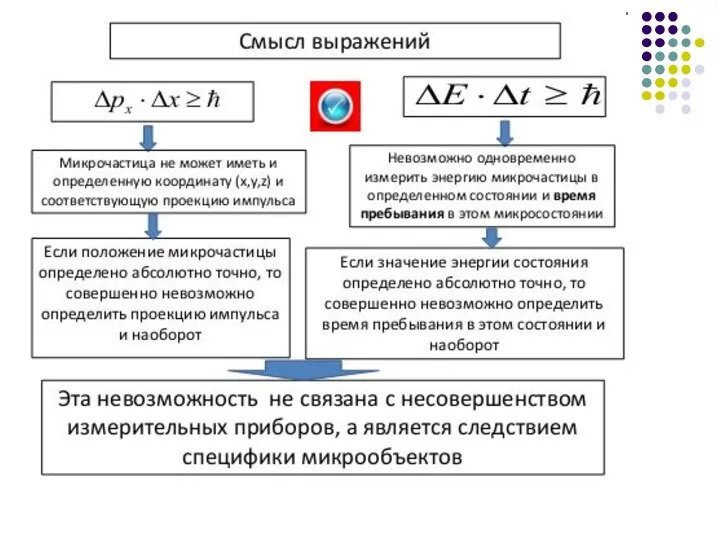
- 7. Утверждение о том, что произведение неопределенности значений двух сопряженных величин не может быть по порядку меньше
- 8. Соотношения неопределенности Гейзенберга показывают, что волновая механика дает возможность одновременно использовать два, казалось бы, противоречащих друг
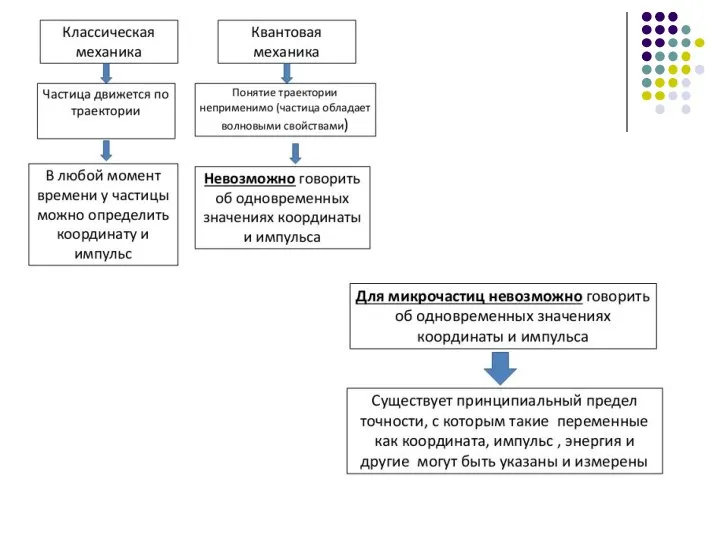
- 11. Соотношение неопределенностей является квантовым ограничением применимости классической механики к микрообъектам 1. Невозможно состояние, в котором частица
- 12. Понятие о зонной теории твердых тел. Основные положения Твердое тело – многоядерная и многоэлектронная система, в
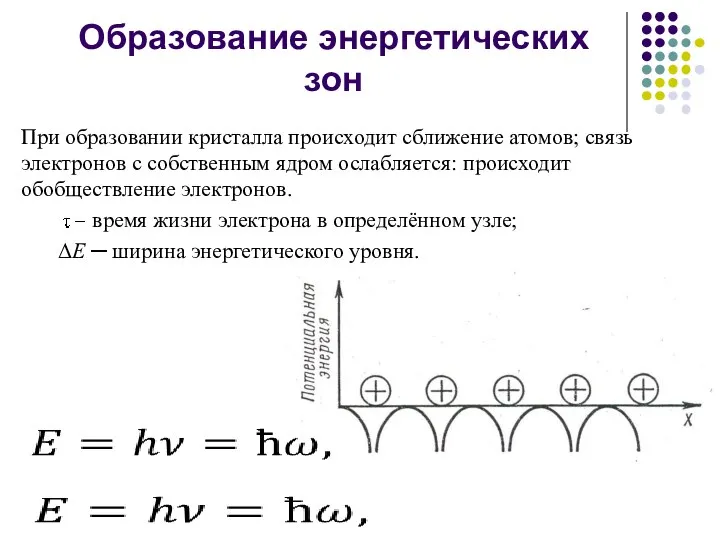
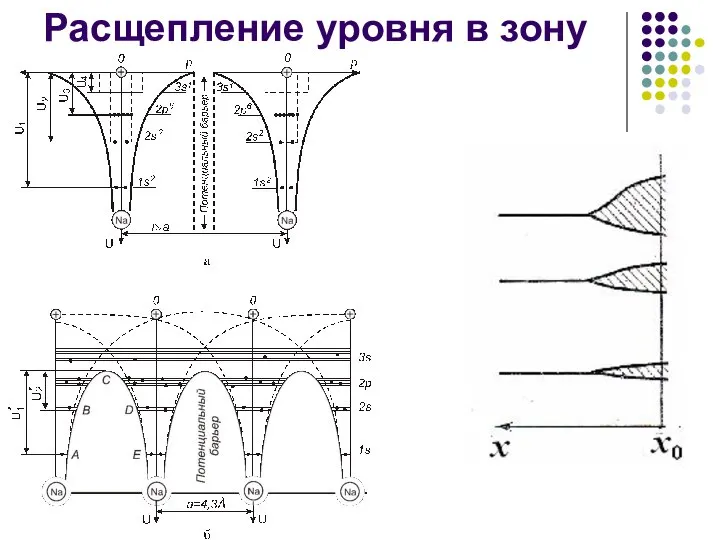
- 13. Образование энергетических зон При образовании кристалла происходит сближение атомов; связь электронов с собственным ядром ослабляется: происходит
- 14. Расщепление уровня в зону
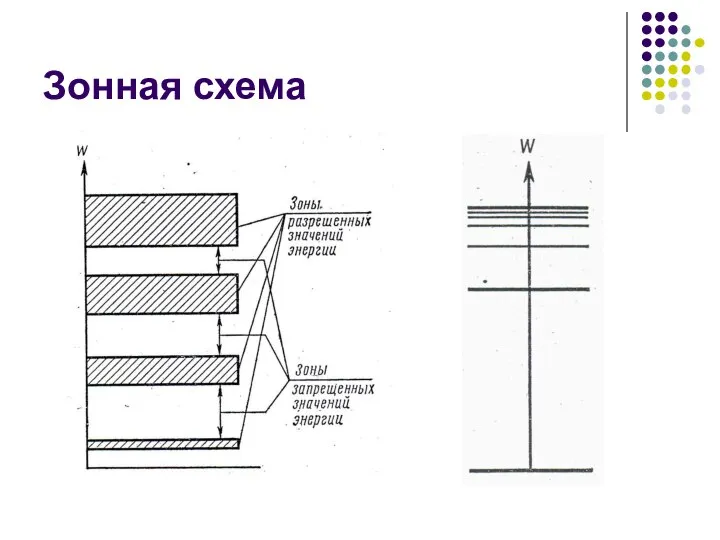
- 15. Зонная схема
- 16. Особенности зонной схемы Зоны энергетических уровней образуются как уровнями, занятыми электронами, так и свободными уровнями. В
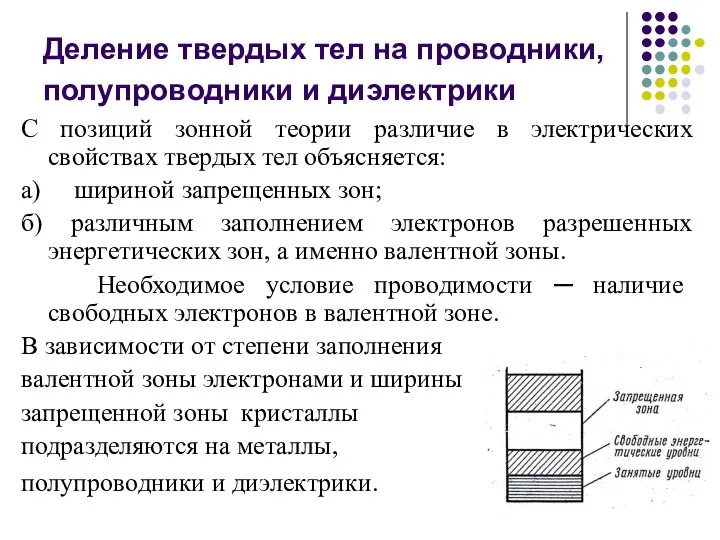
- 17. Деление твердых тел на проводники, полупроводники и диэлектрики С позиций зонной теории различие в электрических свойствах
- 18. Электропроводность металлов Согласно квантовой теории проводимость металлов время релаксации. В проводимости участвуют не все электроны, а
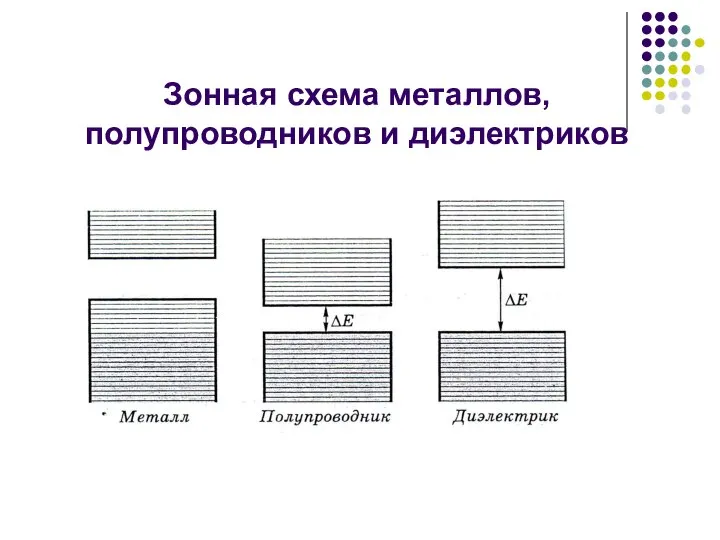
- 19. Зонная схема металлов, полупроводников и диэлектриков
- 20. Собственная проводимость полупроводников У полупроводников и диэлектриков валентная зона полностью заполнена электронами. При T = 0
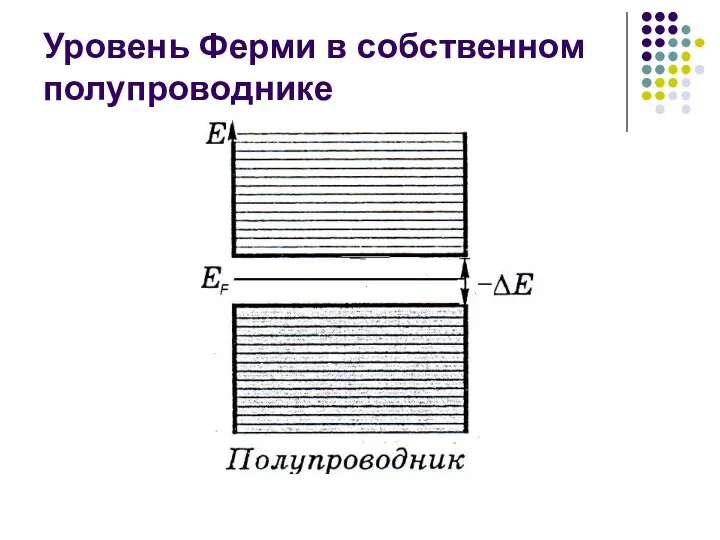
- 21. Уровень Ферми в собственном полупроводнике
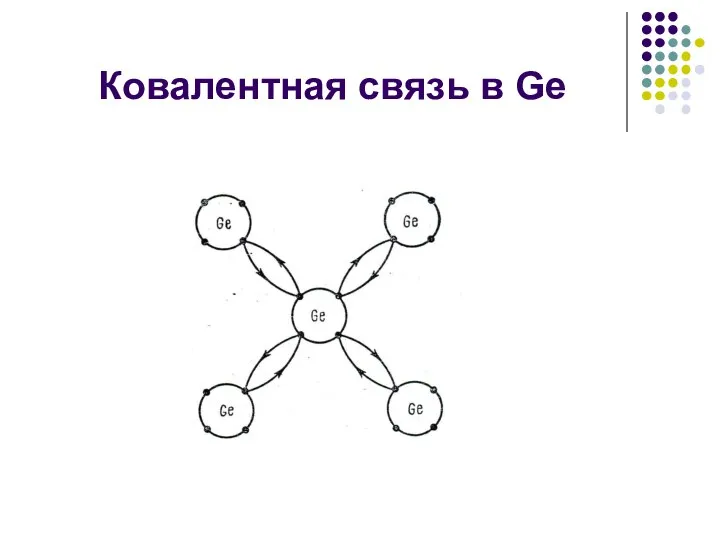
- 22. Ковалентная связь в Ge
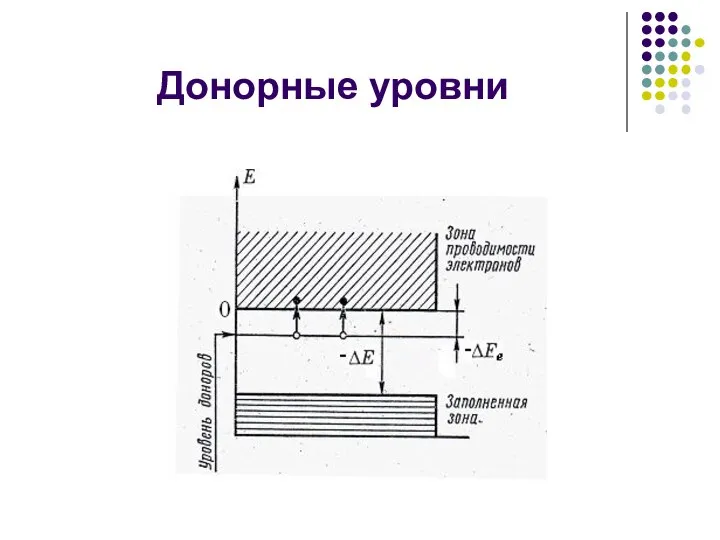
- 23. Донорные уровни
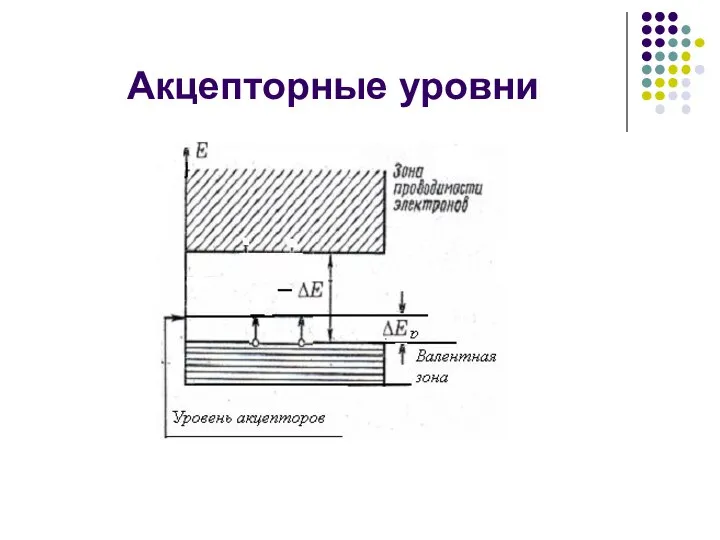
- 24. Акцепторные уровни
- 26. Скачать презентацию











 Презентация на тему Сила
Презентация на тему Сила  Оценка одновременно нескольких параметров
Оценка одновременно нескольких параметров Давление. Обобщение
Давление. Обобщение Поляризация света
Поляризация света Движение тела, брошенного вертикально вверх
Движение тела, брошенного вертикально вверх Магнитное поле
Магнитное поле Механическое движение в живой и неживой природе
Механическое движение в живой и неживой природе Естествознание как источник развития техники
Естествознание как источник развития техники Методы подобия физических процессов
Методы подобия физических процессов Определение скоростей и ускорений точек АТТ при плоском движении
Определение скоростей и ускорений точек АТТ при плоском движении Уровни описания технических систем
Уровни описания технических систем Солнечная энергия
Солнечная энергия Классификация томографов и магнитов
Классификация томографов и магнитов Кипение. Удельная теплота парообразования и конденсации
Кипение. Удельная теплота парообразования и конденсации Задачи ЕГЭ и олимпиад по молекулярной физике и термодинамике
Задачи ЕГЭ и олимпиад по молекулярной физике и термодинамике Бумажные тиски. Вторичная (и окончательная) теория
Бумажные тиски. Вторичная (и окончательная) теория Определение коэффициента силы трения
Определение коэффициента силы трения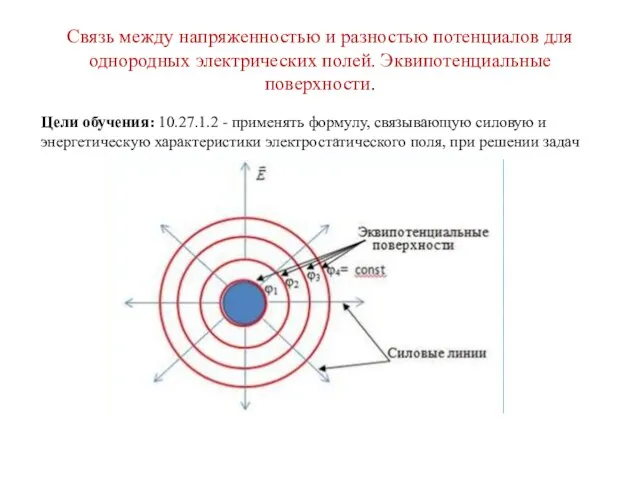 Связь между напряженностью и разностью потенциалов для однородных электрических полей. Эквипотенциальные поверхности
Связь между напряженностью и разностью потенциалов для однородных электрических полей. Эквипотенциальные поверхности законы ньютона
законы ньютона Апробация системы цифрового сопровождения индивидуализированного образования в условиях смешанного очного и удаленного обучения
Апробация системы цифрового сопровождения индивидуализированного образования в условиях смешанного очного и удаленного обучения Тепловые балансы ВТУ, их разновидности. Тепловой баланс теплотехнологического реактора
Тепловые балансы ВТУ, их разновидности. Тепловой баланс теплотехнологического реактора Альтернативная энергетика
Альтернативная энергетика Розробка макета RC-генератора ультразвукового діапазону
Розробка макета RC-генератора ультразвукового діапазону Ионное испарение. Механизм распыления при ионном испарении. Катодное испарение: диодное, диодное со смещением и триодное
Ионное испарение. Механизм распыления при ионном испарении. Катодное испарение: диодное, диодное со смещением и триодное Магнитное взаимодействие Изучение свойств магнита Учитель И.А. Попова
Магнитное взаимодействие Изучение свойств магнита Учитель И.А. Попова Қазақ танымындағы шаңырақ концептісі
Қазақ танымындағы шаңырақ концептісі Формула Планка
Формула Планка Магнитное поле
Магнитное поле