Анализ сложной линейной электрической цепи постоянного тока

Содержание
1. Основные теоретические сведения: первый и второй законы Кирхгофа, метод контурных токов, баланс мощностей.
2. Практическое задание: расчет сложной линейной цепи постоянного тока.
3. Математическая поддержка: решение систем уравнений.
4. Задачи для самостоятельного решения.
Продолжить

Основные теоретические сведения
Электрической цепью называют совокупность тел и сред, образующих замкнутые пути для протекания электрического тока.
Обычно физические объекты и среду, в которой протекает электрический ток, упрощают до условных элементов и связей между ними. Тогда определение цепи можно сформулировать как совокупность различных элементов, объединенных друг с другом соединениями или связями, по которым может протекать электрический ток.
Продолжить

Элементами электрической цепи являются источники электрической энергии, активные и реактивные сопротивления.
Связи в электрической цепи изображаются линиями и по смыслу соответствуют идеальным проводникам с нулевым сопротивлением.
Связи элементов электрической цепи обладают топологическими свойствами, т.е. они не изменяются при любых преобразованиях, производимых без разрыва связей.
Продолжить

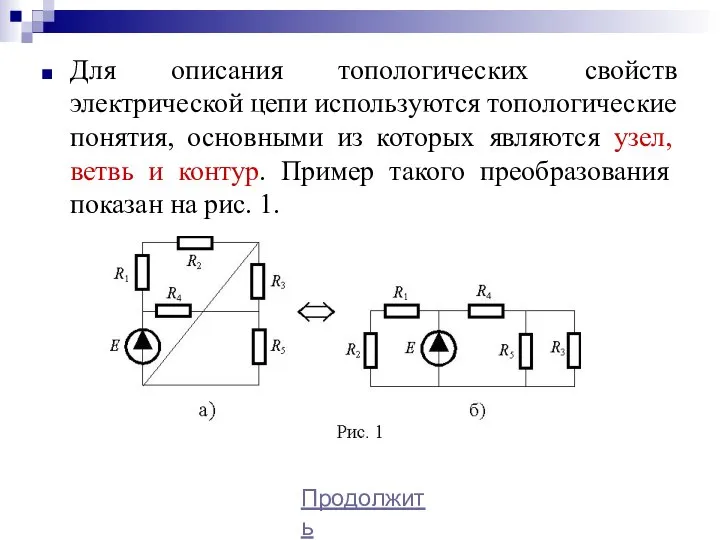
Для описания топологических свойств электрической цепи используются топологические понятия, основными из которых являются узел, ветвь и контур. Пример такого преобразования показан на рис. 1.
Продолжить

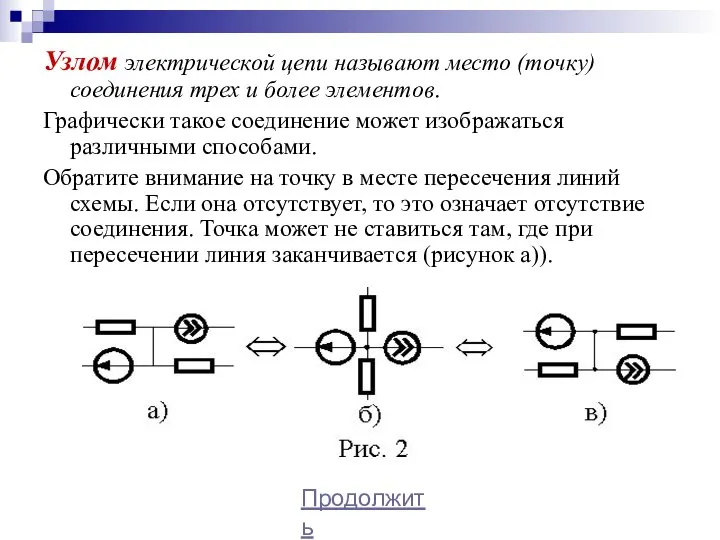
Узлом электрической цепи называют место (точку) соединения трех и более элементов.
Графически такое соединение может изображаться различными способами.
Обратите внимание на точку в месте пересечения линий схемы. Если она отсутствует, то это означает отсутствие соединения. Точка может не ставиться там, где при пересечении линия заканчивается (рисунок а)).
Продолжить

Ветвью называют совокупность связанных элементов электрической цепи между двумя узлами.
Ветвь по определению содержит элементы, поэтому вертикальные связи рис.2 а) и б) ветвями не являются. Не является ветвью и диагональная связь рис.1а).
Продолжить

Контуром (замкнутым контуром) называют совокупность ветвей, образующих путь, при перемещении вдоль которого мы можем вернуться в исходную точку, не проходя более одного раза по каждой ветви и по каждому узлу.
По определению различные контуры электрической цепи должны отличаться друг от друга по крайней мере одной ветвью.
Количество контуров, которые могут быть образованы для данной электрической цепи ограничено и определено.
Продолжить

Законы Кирхгофа являются одной из форм закона сохранения энергии и потому относятся к фундаментальным законам природы.
Первый закон Кирхгофа является следствием принципа непрерывности электрического тока, в соответствии с которым суммарный поток зарядов через любую замкнутую поверхность равен нулю, т.е. количество зарядов выходящих через эту поверхность должно быть равно количеству входящих зарядов. Основание этого принципа очевидно, т.к. при нарушении его электрические заряды внутри поверхности должны были бы либо исчезать, либо возникать без видимых причин.
Продолжить

Первый закон Кирхгофа
Алгебраическая сумма токов в узле электрической цепи равна нулю:
При этом токи, направленные к узлу, записываются со знаком «плюс», а токи, направленные от узла, - со знаком «минус».
-I1+ I2+ I3- I4 = 0
Продолжить

Второй закон Кирхгофа
Алгебраическая сумма падений напряжений в ветвях любого замкнутого контура равна алгебраической сумме ЭДС, действующих в этом контуре,:
Направление обхода контура выбираем произвольно (в примере против часовой стрелки).
I1R1+I2R2-I3R3-I4R4=
=E1-E2
Примечание: знак + для ЭДС выбирается в том случае, если направление ее действия совпадает с направлением обхода контура, а для напряжений на резисторах знак + выбирается, если в них совпадают направление протекания тока и направление обхода.
Продолжить

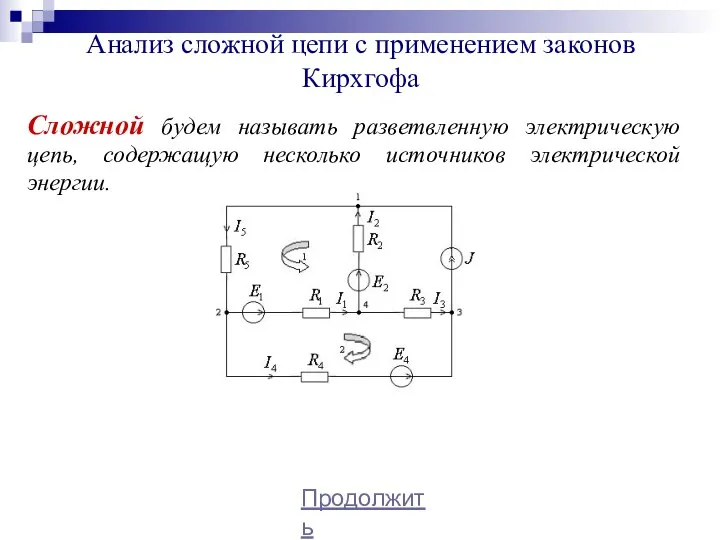
Анализ сложной цепи с применением законов Кирхгофа
Сложной будем называть разветвленную электрическую цепь, содержащую несколько источников электрической энергии.
Продолжить

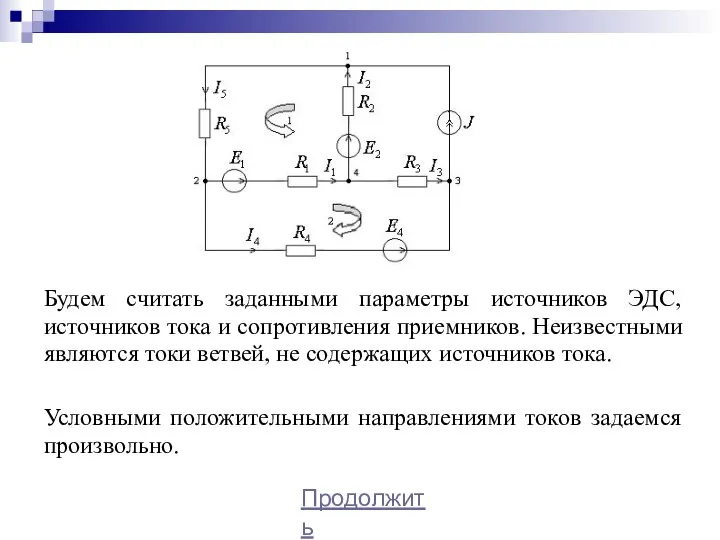
Будем считать заданными параметры источников ЭДС, источников тока и сопротивления приемников. Неизвестными являются токи ветвей, не содержащих источников тока.
Условными положительными направлениями токов задаемся произвольно.
Продолжить

Введем обозначения:
k – число узлов схемы
m – число ветвей, не содержащих источников тока
В рассматриваемом примере k = 4, m = 5.
Расчет и анализ сложной электрической цепи основан на уравнениях, составляемых по 1 и 2 законам Кирхгофа, в количестве, достаточном для решения системы. Все уравнения в системе должны быть независимыми.
Число независимых уравнений, составляемых по 1 закону Кирхгофа, на единицу меньше числа узлов:
Продолжить

Число независимых уравнений, составляемых по второму закону Кирхгофа:
Независимость уравнений по второму закону Кирхгофа будет обеспечена, если контуры выбирать таким образом, чтобы каждый последующий контур отличался от предыдущего хотя бы одной новой ветвью.
Для контура, содержащего ветвь с источником тока, уравнение не составляется.
Направление обхода – произвольное.
Продолжить

Таким образом, порядок анализа сложной цепи с применением законов Кирхгофа следующий:
1) выбирают произвольно положительные условные направления токов в ветвях;
2) составляют (k-1) независимых уравнений по первому закону Кирхгофа.
3) выбирают произвольно направления обхода независимых контуров,
4) составляют m-(k-1) независимых уравнений по второму закону Кирхгофа,
5) решают совместно полученную систему уравнений.
Продолжить

Метод контурных токов
Введем новые условные (фиктивные) неизвестные, называемые «контурными токами».
«Контурный» ток замыкается по соответствующему контуру.
Составляются уравнения по 2-му закону Кирхгофа. Для того, чтобы уравнения были независимыми, каждый последующий контур должен отличаться от предыдущих хотя бы одной новой ветвью.
Для контура, содержащего ветвь с источником тока, уравнение не составляется.
Продолжить

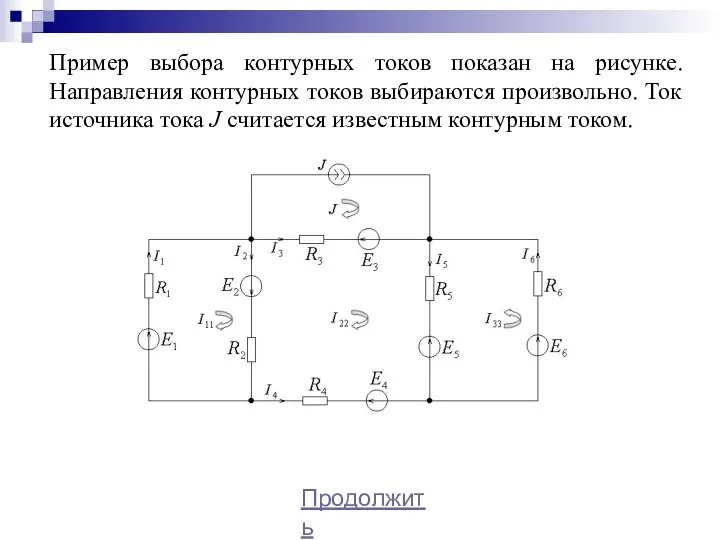
Пример выбора контурных токов показан на рисунке. Направления контурных токов выбираются произвольно. Ток источника тока J считается известным контурным током.
Продолжить

При использовании данного метода уравнения составляются только по второму закону Кирхгофа.
Метод контурных токов позволяет сократить число совместно решаемых в системе уравнений до
При этом учитывается, что падение напряжения на отдельных участках цепи создаются совместным действием контурных токов, проходящих через данные участки.
Продолжить

Уравнение для К-го контура любой схемы по методу контурных токов записывается как:
Здесь I11, I22, Ipp, Ikk, Ill,… - контурные токи 1-го, 2-го, р-го, к-го, l-го контуров,
Ekk - алгебраическая сумма ЭДС всех ветвей, составляющих к-ый контур,
Rkk - арифметическая сумма сопротивлений ветвей, составляющих рассматриваемый к-ый контур. Значения Rkk всегда положительны.
Rk1, Rk2, …, Rkp, Rkl - сопротивления ветвей, смежных между соответственно к-ым и первым, к-ым и вторым, к-ым и l-ым и т.д. контурами,
Rkp>0, если направления токов Ipp, Ikk через рассматриваемую ветвь совпадают. В противном случае Rkp<0.
Продолжить

Система уравнений по методу контурных токов сравнительно легко решается с помощью определителей.
После решения системы и определения контурных токов I11, I22, I33 переходим к определению токов отдельных ветвей.
Ток какой-либо ветви определяется как алгебраическая сумма контурных токов через данную ветвь. Со знаком «плюс» будем записывать контурный ток, совпадающий по направлению с током данной ветви.
Продолжить

Баланс мощностей
Уравнение энергетического баланса:
Σ RI2 = Σ EI
Произведение записываются с «+», если направления ЭДС и тока совпадают, и с «-», если направления противоположны.
Продолжить

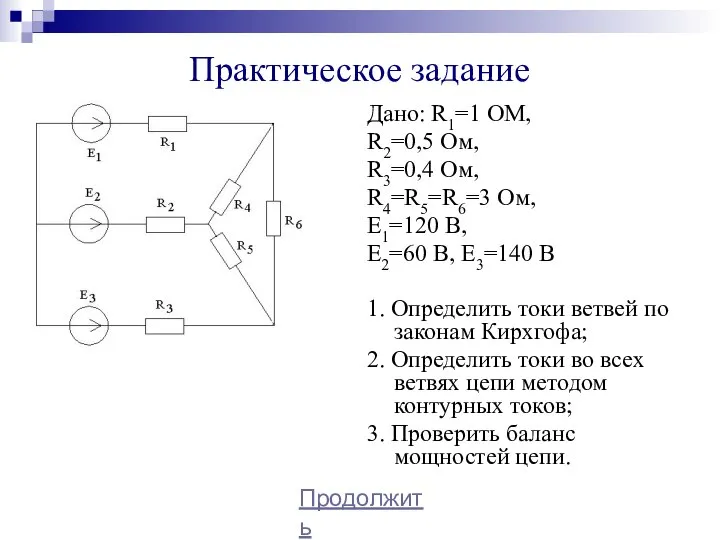
Практическое задание
Дано: R1=1 ОМ,
R2=0,5 Ом,
R3=0,4 Ом,
R4=R5=R6=3 Ом,
Е1=120 В,
Е2=60 В, Е3=140 В
1. Определить токи ветвей по законам Кирхгофа;
2. Определить токи во всех ветвях цепи методом контурных токов;
3. Проверить баланс мощностей цепи.
Продолжить

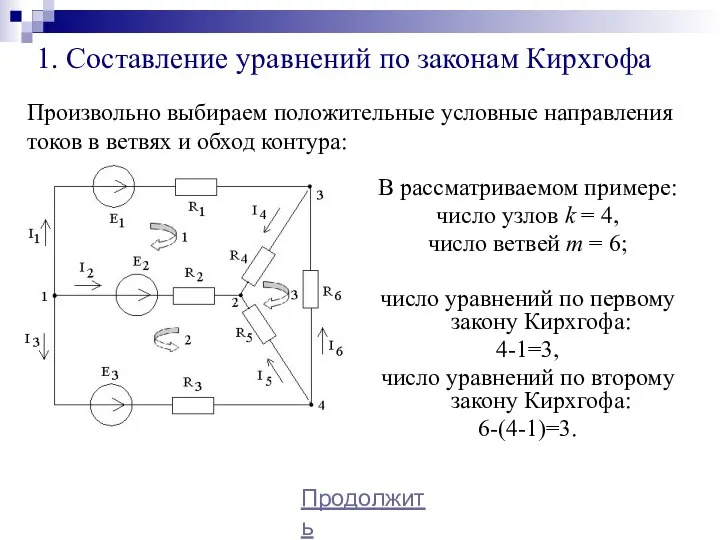
1. Составление уравнений по законам Кирхгофа
В рассматриваемом примере:
число узлов k = 4,
число ветвей m = 6;
число уравнений по первому закону Кирхгофа:
4-1=3,
число уравнений по второму закону Кирхгофа:
6-(4-1)=3.
Произвольно выбираем положительные условные направления токов в ветвях и обход контура:
Продолжить

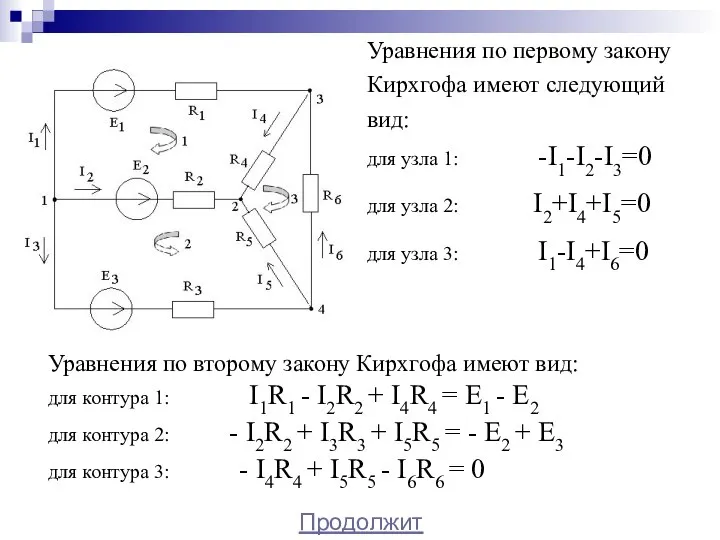
Уравнения по первому закону Кирхгофа имеют следующий вид:
для узла 1: -I1-I2-I3=0
для узла 2: I2+I4+I5=0
для узла 3: I1-I4+I6=0
Уравнения по второму закону Кирхгофа имеют вид:
для контура 1: I1R1 - I2R2 + I4R4 = E1 - E2
для контура 2: - I2R2 + I3R3 + I5R5 = - E2 + E3
для контура 3: - I4R4 + I5R5 - I6R6 = 0
Продолжить

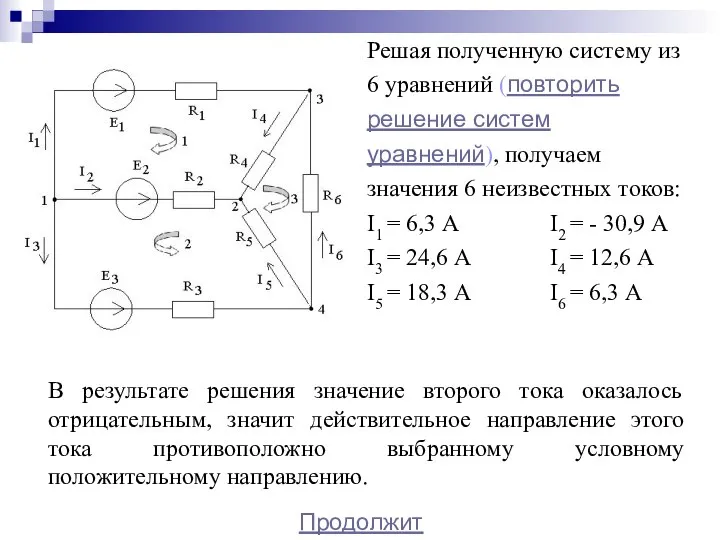
Решая полученную систему из 6 уравнений (повторить решение систем уравнений), получаем значения 6 неизвестных токов:
I1 = 6,3 А I2 = - 30,9 А
I3 = 24,6 А I4 = 12,6 А
I5 = 18,3 А I6 = 6,3 А
В результате решения значение второго тока оказалось отрицательным, значит действительное направление этого тока противоположно выбранному условному положительному направлению.
Продолжить

2. Определение токов во всех ветвях цепи методом контурных токов
Вводим новые неизвестные – контурные токи I11, I22, I33 и составляем уравнения для данных контуров по второму закону Кирхгофа:
E1-E2=(R1+R2+R4)I11+R2I22-R4I33
-E2+E3=(R2+R3+R5)I22+R2I11+R5I33
0=(R4+R5+R6)I33-R4I11+R5I22
Продолжить

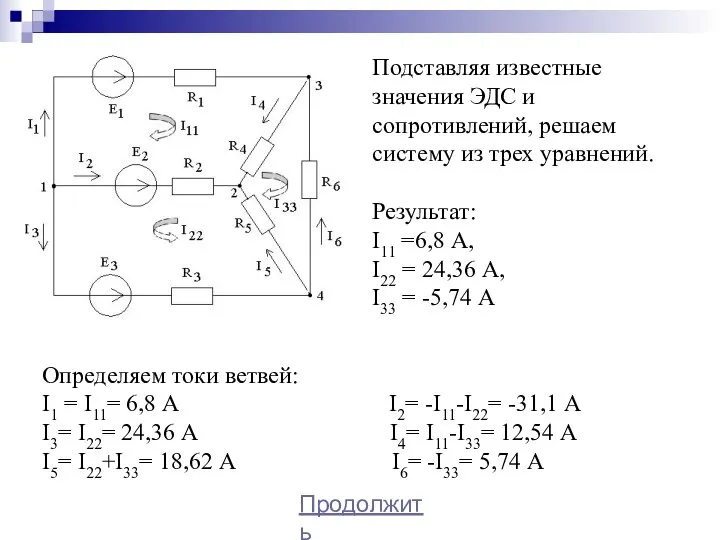
Подставляя известные значения ЭДС и сопротивлений, решаем систему из трех уравнений.
Результат:
I11 =6,8 А,
I22 = 24,36 А,
I33 = -5,74 А
Определяем токи ветвей:
I1 = I11= 6,8 А I2= -I11-I22= -31,1 А
I3= I22= 24,36 А I4= I11-I33= 12,54 А
I5= I22+I33= 18,62 А I6= -I33= 5,74 А
Продолжить

3. Проверка баланса мощностей
R1I12+R2I22+R3I32+R4I42+R5I52+R6I62= = E1I1+E2I2+E3I3
Поставляем значения и определяем:
2365,56 = 2360,4
Продолжить

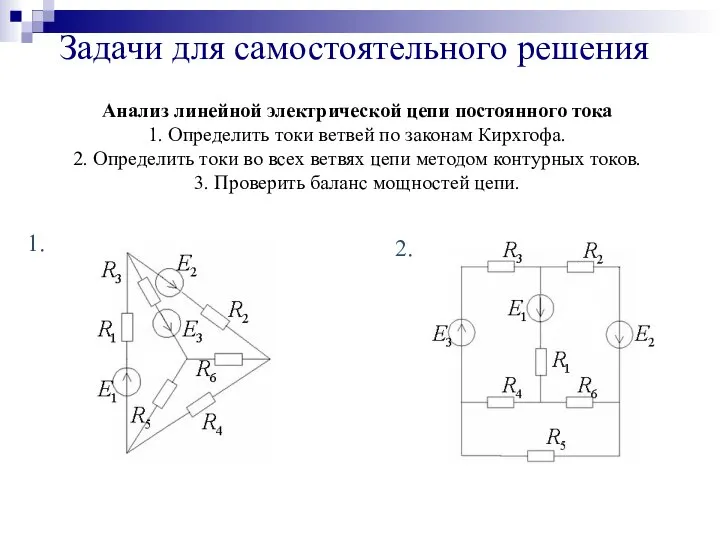
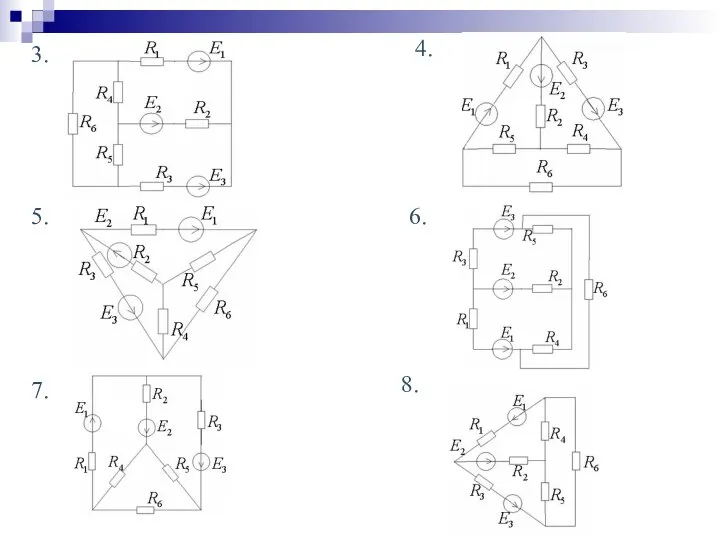
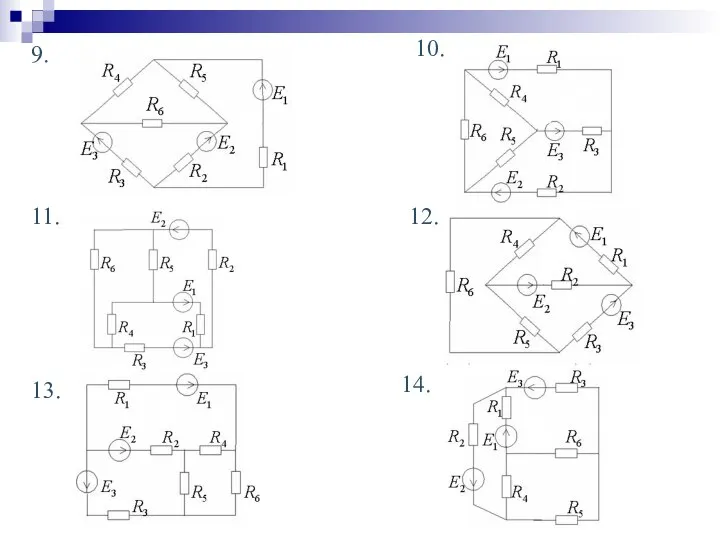
Задачи для самостоятельного решения
Анализ линейной электрической цепи постоянного тока
1. Определить токи ветвей по законам Кирхгофа.
2. Определить токи во всех ветвях цепи методом контурных токов.
3. Проверить баланс мощностей цепи.
1.
2.

5.
6.
7.
8.
3.
4.

11.
12.
13.
14.
9.
10.

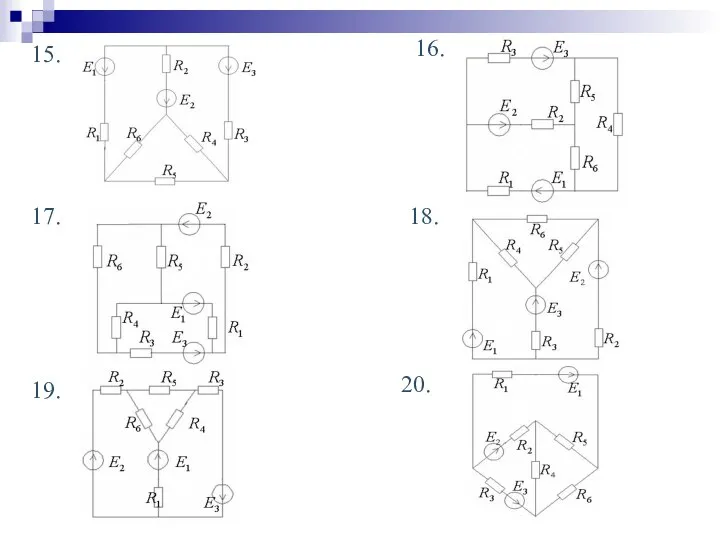
17.
18.
19.
20.
15.
16.

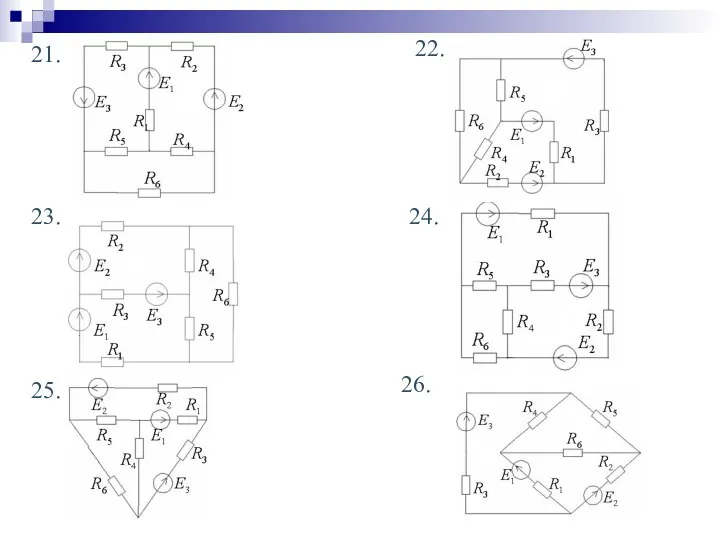
23.
24.
25.
26.
21.
22.

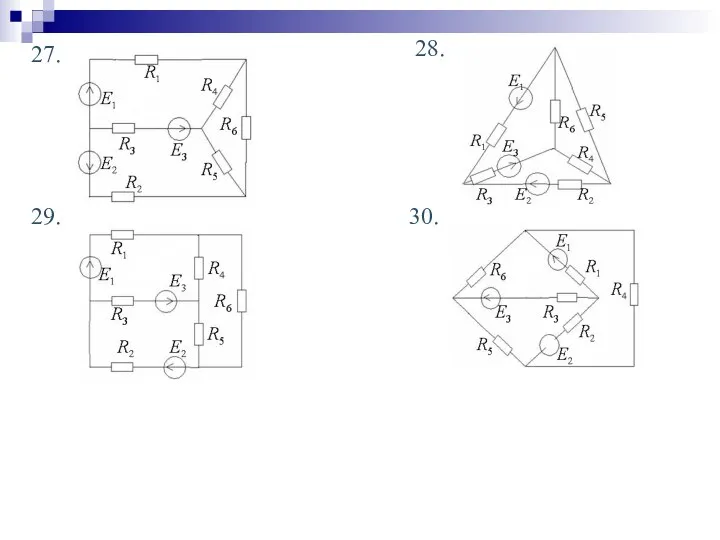
29.
30.
27.
28.

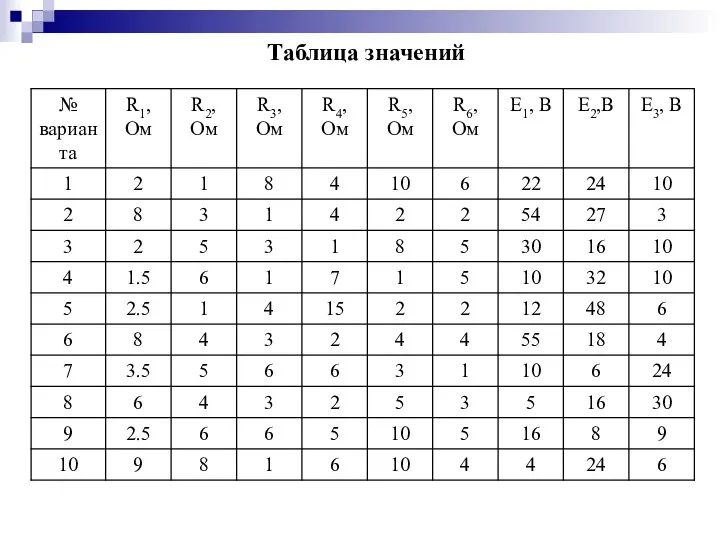
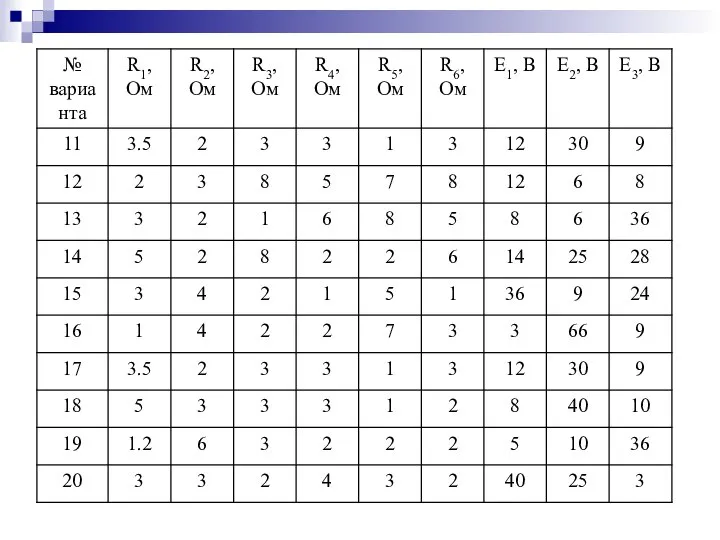
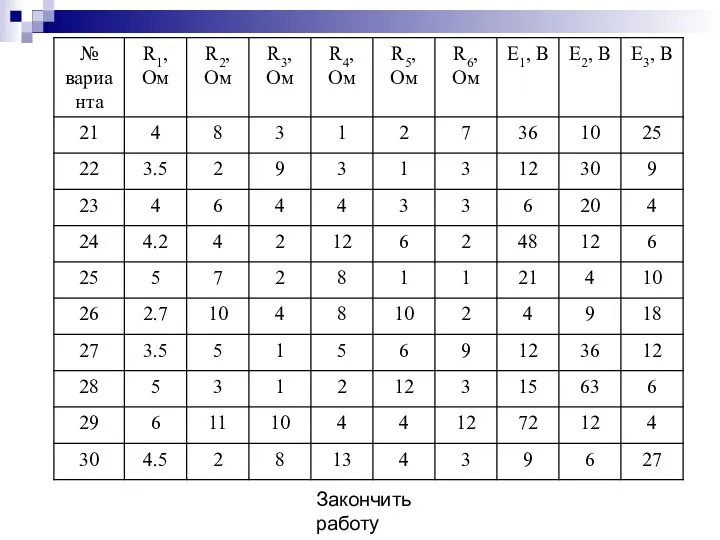
Таблица значений

Закончить работу

Решение систем уравнений со многими неизвестными
В данной задаче необходимо решить систему из шести уравнений с шестью неизвестными.
Принцип решения системы - выражать из каждого уравнения какую-либо переменную и поставлять это выражение в последующие уравнения.
Главное– последовательность и аккуратность при решении.
Продолжить

Сначала подставим в систему известные значения ЭДС и сопротивлений:
-I1-I2-I3=0
I2+I4+I5=0
I1-I4+I6=0
I1 – 0,5I2 + 3I4 = 120 – 60
- 0,5 I2 + 0,4 I3 + 3I5 = - 60 +140
- 3I4 + 3I5 - 3I6 = 0
Из первого уравнения выражаем переменную: I1=-I2-I3
И подставляем правую часть данного выражения во все последующие уравнения.
Продолжить

I1=-I2-I3
I2+I4+I5=0
(-I2-I3) -I4+I6=0
(-I2-I3) – 0,5I2 + 3I4 = 120 – 60
- 0,5 I2 + 0,4 I3 + 3I5 = - 60 +140
- 3I4 + 3I5 - 3I6 = 0
Из второго уравнения выражаем переменную: I4=-I2-I5
I1=-I2-I3
I4=-I2-I5
(-I2-I3) –(-I2-I5)+I6=0
(-I2-I3) – 0,5I2 + 3(-I2-I5) = 120 – 60
- 0,5 I2 + 0,4 I3 + 3I5 = - 60 +140
- 3(-I2-I5) + 3I5 - 3I6 = 0
Продолжить

Рассмотрим отдельно третье уравнение, раскроем скобки, приведем подобные слагаемые и выразим одно из неизвестных:
(-I2-I3) –(-I2-I5)+I6=0
-I2-I3+I2+I5+I6=0
-I3+I5+I6=0
I6= I3 - I5
Также отдельно рассмотрим четвертое уравнение:
-I2-I3 – 0,5I2 + 3(-I2-I5) = 60
-I2-I3 – 0,5I2 - 3I2-3I5 = 60
- 4,5I2 - I3 -3I5 = 60
I3 = - 4,5I2 -3I5 - 60
Продолжить

Преобразуем пятое уравнение:
- 0,5 I2 + 0,4 I3 + 3I5 = - 60 +140
- 0,5 I2 + 0,4(- 4,5I2 -3I5 - 60) + 3I5 = 80
- 0,5 I2 – 1,8 I2 -1,2 I5 - 24 + 3 I5 = 80
- 2,3 I2 + 1,8 I5 = 80 + 24
I5 = (104 + 2,3 I2 ) / 1,8
I5 = 57,8 + 1,28 I2
Продолжить

Преобразуем шестое уравнение:
- 3(-I2-I5) + 3I5 – 3(I3 - I5) = 0
3I2 + 3I5 + 3I5 – 3I3 + 3I5 = 0
3I2 – 3I3 + 9I5 = 0
3I2 – 3(- 4,5I2 -3I5 - 60) + 9I5 = 0
3I2 + 13,5 I2 + 9I5 + 180 + 9I5 = 0
16,5 I2 + 18 I5 + 180 = 0
16,5 I2 + 18 (57,8 + 1,28 I2) + 180 = 0
16,5 I2 + 1040,4 + 23,04 I2 + 180 = 0
39,54 I2 + 1220,4 = 0
I2 = - 30,9
Продолжить