Слайд 11Характеристика системы GAP
Cистема поставляется вместе с исходными текстами, которые написаны на двух

языках: ядро системы написано на Си, а библиотека функций - на специальном языке, также называемом GAP, который по синтаксису напоминает Pascal, однако является объектно-ориентированным языком. Помимо уже упомянутых пакетов, система состоит из следующих четырех основных компонент:
ядра системы, обеспечивающего поддержку языка GAP, работу с системой в программном и интерактивном режиме;
библиотеки функций, в которой реализованы разнообразные алгебраические алгоритмы (более 4000 пользовательских функций, более 140000 строк программ на языке GAP);
библиотеки данных, включая, например, библиотеку всех групп порядка не более 2000 (за исключением 49487365422 групп порядка 1024, точное количество которых, кстати, также было определено с помощью системы GAP), библиотеку примитивных групп подстановок, таблицы характеров конечных групп и т.д., что в совокупности составляет эффективное средство для выдвижения и тестирования научных гипотез;
обширной (около полутора тысяч страниц) документации, доступной в разнообразных форматах (txt, pdf, html), а также через Интернет.





















 Интерференция, дифракция, поляризация
Интерференция, дифракция, поляризация Определение температуры вспышки в закрытом тигле. Лабораторная работа
Определение температуры вспышки в закрытом тигле. Лабораторная работа Электрические машины
Электрические машины Презентация на тему Источники света. Распространение света
Презентация на тему Источники света. Распространение света  Рентгеновская астрономия
Рентгеновская астрономия Билет № 1, 4 (вопрос 3). Задача на формулу силы Лоренца
Билет № 1, 4 (вопрос 3). Задача на формулу силы Лоренца История телеграфа
История телеграфа Мир вокруг нас
Мир вокруг нас Определение эффекта Томпсона
Определение эффекта Томпсона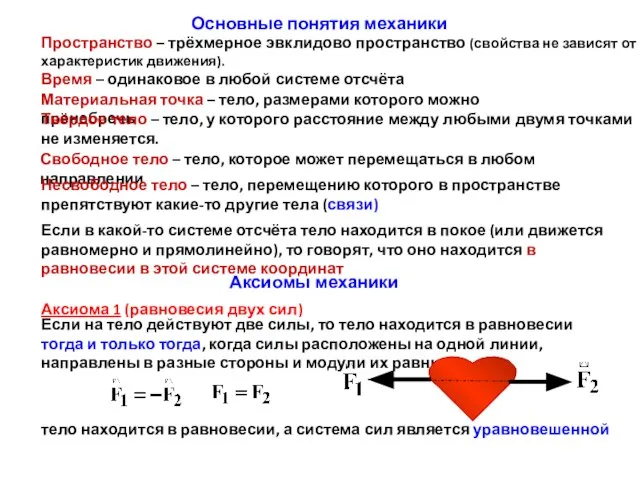 Аксиомы механики
Аксиомы механики Презентация на тему Волны. Звуковые волны. Звук
Презентация на тему Волны. Звуковые волны. Звук  Световые кванты
Световые кванты Холодильные машины
Холодильные машины Наблюдение интерференции и дифракции свет
Наблюдение интерференции и дифракции свет Юные физики. Игра. 7 класс
Юные физики. Игра. 7 класс Деформація
Деформація Третий этап развития естествознания: Современное естествознание (с начала XX века и до наших дней)
Третий этап развития естествознания: Современное естествознание (с начала XX века и до наших дней) Презентация на тему Плавление и кристаллизация
Презентация на тему Плавление и кристаллизация  Расчет на прочность при кручении
Расчет на прочность при кручении Резонансные методы передачи электрической энергии
Резонансные методы передачи электрической энергии Домашнее задание по физике
Домашнее задание по физике Игра-КВН Первый урок в 8 классе
Игра-КВН Первый урок в 8 классе Невидимая сила
Невидимая сила Презентация на тему Механическая работа и мощность
Презентация на тему Механическая работа и мощность  Физические характеристики сигнала
Физические характеристики сигнала Энергетические балансы ВТУ
Энергетические балансы ВТУ Звёздный час. Игра по физике
Звёздный час. Игра по физике