Содержание
- 2. Разреженный газ – газ, существующий при не слишком низких температурах и довольно малых давлениях.
- 3. Идеальный газ – это физическая модель газа, взаимодействие, между молекулами которого пренебрежительно мало. - вводится для
- 4. УСЛОВИЯ ИДЕАЛЬНОСТИ ГАЗА:
- 5. СВОЙСТВА ИДЕАЛЬНОГО ГАЗА: - взаимодействие между молекулами пренебрежительно мало; - расстояние между молекулами много больше размеров
- 6. Система, состоящая из большого числа частиц, характеризуется через
- 7. В 1860 году английский физик Дж. Максвелл теоретически обосновал распределение молекул по скоростям. В 1920 году
- 8. Обозначим модули скоростей отдельных молекул через ʋ1, ʋ2, ʋ3,…, ʋn , где n - число молекул
- 9. В теории газов часто используется понятие средней кинетической энергии молекул.
- 10. ОСНОВНОЕ УРАВНЕНИЕ МКТ ГАЗА
- 11. Давление газа на стенки сосуда пропорцио-нально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.
- 12. - средний квадрат скорости молекул (м2/с2) ρ (ро) - плотность газа (кг/м3) где Р - давление
- 13. Формула для расчета концентрации молекул: где N - число молекул газа, V - объем газа (м3)
- 14. РЕШЕНИЕ ЗАДАЧ Задача 1 Как изменится давление газа, если концентра-ция его молекул увеличится в 3 раза,
- 16. Скачать презентацию













 Решение задач на закон Ома для однородного участка
Решение задач на закон Ома для однородного участка Презентация на тему Солнце (11 класс)
Презентация на тему Солнце (11 класс)  7_Sily_v_prirode_sila_tyazhesti_ves (1)
7_Sily_v_prirode_sila_tyazhesti_ves (1) Понятия релятивистской динамики - масса, импульс. Закон взаимодействия массы и энергии. Связь между импульсом и энергией тела
Понятия релятивистской динамики - масса, импульс. Закон взаимодействия массы и энергии. Связь между импульсом и энергией тела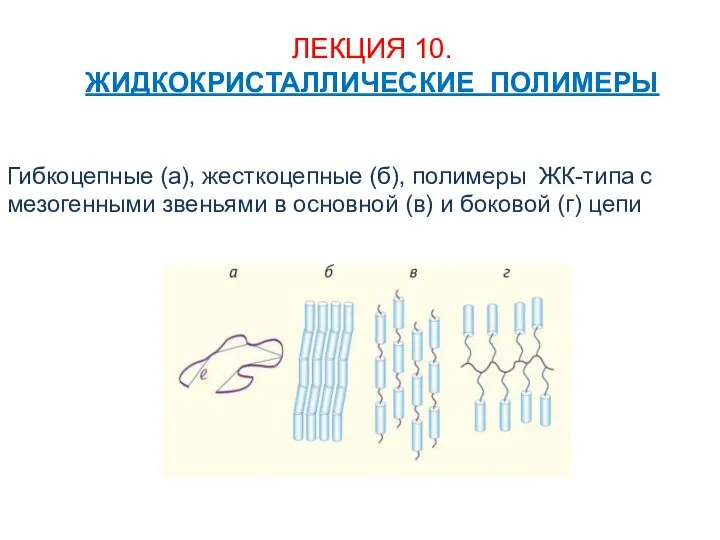 Жидкокристаллические полимеры
Жидкокристаллические полимеры Презентация на тему Тепловые электростанции
Презентация на тему Тепловые электростанции  Презентация к уроку _Инерциальные системы отсчета
Презентация к уроку _Инерциальные системы отсчета Презентация на тему Тепловое равновесие
Презентация на тему Тепловое равновесие  Презентация на тему Тест по теме «Электрический ток в разных средах»
Презентация на тему Тест по теме «Электрический ток в разных средах»  Определение выталкивающей силы, действующей на погруженное в жидкость тело. ЛР №8
Определение выталкивающей силы, действующей на погруженное в жидкость тело. ЛР №8 Усилитель звуковой частоты
Усилитель звуковой частоты Гамма- излучение
Гамма- излучение Электромагнитные колебания. Метод векторных диаграмм. Метод комплексных амплитуд. Переменный ток
Электромагнитные колебания. Метод векторных диаграмм. Метод комплексных амплитуд. Переменный ток Кручение. Основные понятия
Кручение. Основные понятия Напряжённость электрического поля
Напряжённость электрического поля Электризация тел
Электризация тел Puzyrkovaya_kamera
Puzyrkovaya_kamera Элементарные частицы - презентация_
Элементарные частицы - презентация_ Динамическая метеорология. Термический ветер
Динамическая метеорология. Термический ветер Презентация на тему Получение и передача переменного электрического тока
Презентация на тему Получение и передача переменного электрического тока  Байр зүйн холбогч машины тухай
Байр зүйн холбогч машины тухай Квазихимический метод описания дефектов
Квазихимический метод описания дефектов Электрические нагрузки. Методы определения расчетных нагрузок. Тема 2.2
Электрические нагрузки. Методы определения расчетных нагрузок. Тема 2.2 Законы сохранения. Самостоятельная работа
Законы сохранения. Самостоятельная работа Магнитное поле
Магнитное поле Основные понятия теории механизмов и машин
Основные понятия теории механизмов и машин Области применения ультрафиолетового и инфракрасного излучений
Области применения ультрафиолетового и инфракрасного излучений Закон Архимеда
Закон Архимеда