Колебания математического и пружинного маятников

Сегодня на уроке мы узнаем и вспомним:
Какие колебания называют гармоническими
Уравнение гармонических
колебаний
Что такое математический
и пружинный маятник
Что такое фаза колебаний
Формулу для нахождения периода математического и пружинного маятника

Научимся
Определять период маятника по формуле
Записывать и анализировать уравнения колебаний
Определять амплитуду, частоту и период колебаний по уравнению и графику
Определять фазу колебаний

Итак, давайте вспомним один из видов движения – колебательное движение.
Колебательное движение широко распространено в окружающей нас жизни.
Примером такого движения является: движение качелей, маятника часов, вагона на рессорах и т.д.

ПОВТОРЕНИЕ – МАТЬ УЧЕНИЯ!!!
1. Что называют колебаниями?
3.Какие колебания называют свободными?
5.Что такое период? Единица, обозначение, формула.
7.Т = t / N, (c)
2. Какие виды колебаний вы знаете?
4. Какие колебания называют вынужденными?
6. Что такое частота? Единица, обозначение, формула.
8. V = N / t, (Гц)

ПРИВЕСТИ В СООТВЕТСТВИЕ:
Период измеряется в … время одного полного
колебания Частота измеряется в … наибольшее смещение от
положения равновесия
Период – измеряется в … в секундах
Период – это … число колебаний в
единицу времени
Частота – это … в герцах
Вынужденные колебания – … колебания, происходящие
под действием силы

Что такое маятник?
Устройства, в которых могут осуществляться колебательные процесс, называются колебательными системами.
Простейшая такая система – это маятник.
Маятник – любое тело, подвешенное так, что его центр тяжести находиться ниже точки подвеса.
Рассмотрим математический маятник

3º~5º
Маятник ?? - НЕТ
Условия для существования математического маятника
** Длина нити гораздо больше размера груза
** Масса нити мала
** Растяжение нити невелико
Математическим маятником называют тяжелый шарик малого размера, подвешенный на длиной, невесомой нерастяжимой нити.

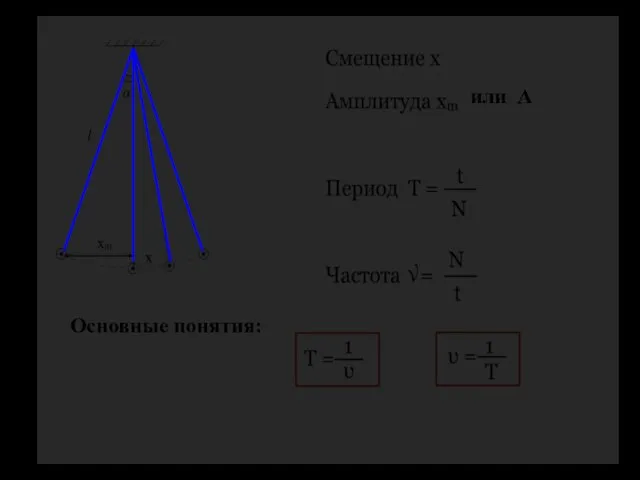
Основные понятия:
или А

Период колебаний математического маятника
Формула Гюйгенса

Пружинный маятник и его основные характеристики
Fупр
Период – Т, с
F тяж Частота – v, Гц
Жесткость пружины – k, Н/м
Масса груза – m, кг
Т = 2π m/k
Под действием силы тяжести груз движется вниз, а под действием силы упругости – вверх.

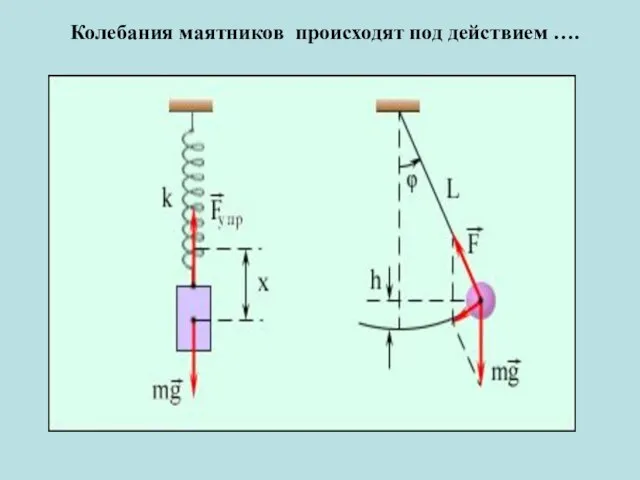
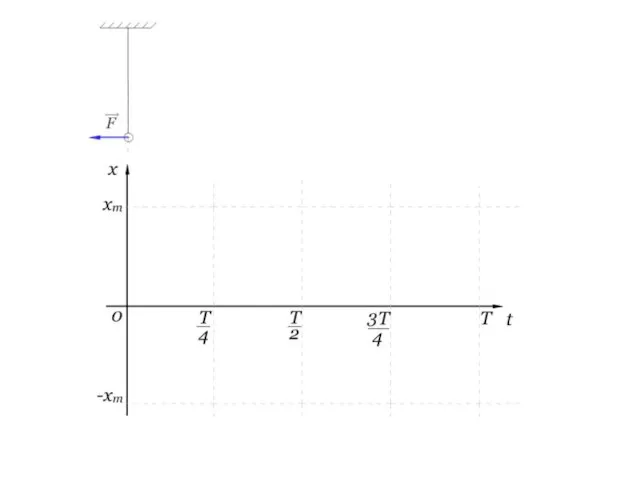
Колебания маятников происходят под действием ….

Выясним, от чего зависит период колебаний нитяного маятника

ПРАКТИЧЕСКАЯ РАБОТА
Измерьте период колебания и длину математического маятника
Измените длину маятника вдвое и вновь измерьте период
Сделайте вывод о зависимости периода маятника от его длины. Заполнить таблицу.

ВЫВОД:
Период математического маятника не зависит от массы груза
Период математического маятника не зависит от амплитуды колебаний
Период колебаний пружинного маятника зависит от массы груза
Период колебаний пружинного маятника зависит от жесткости пружины

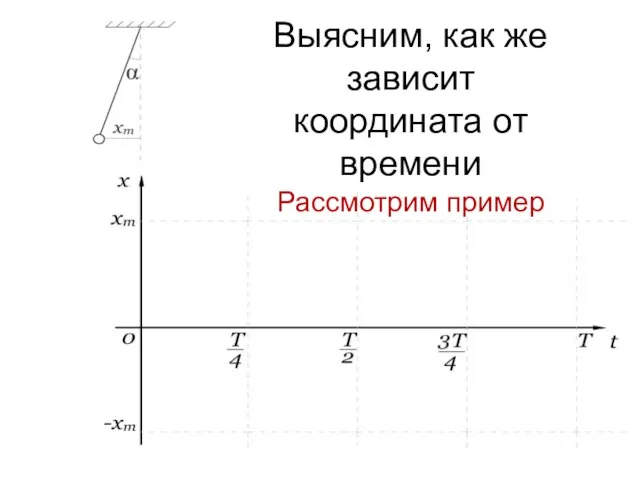
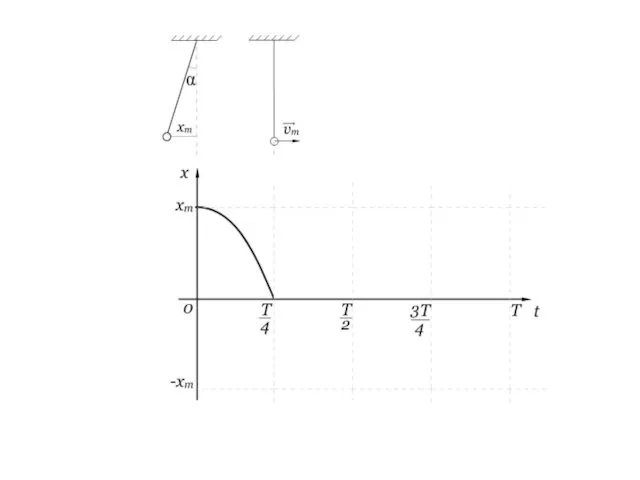
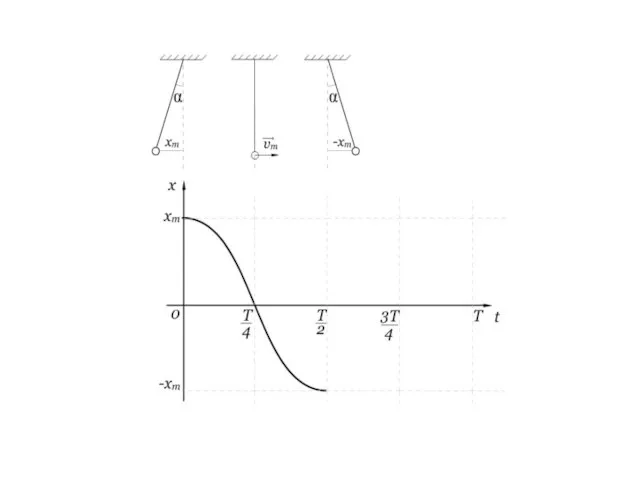
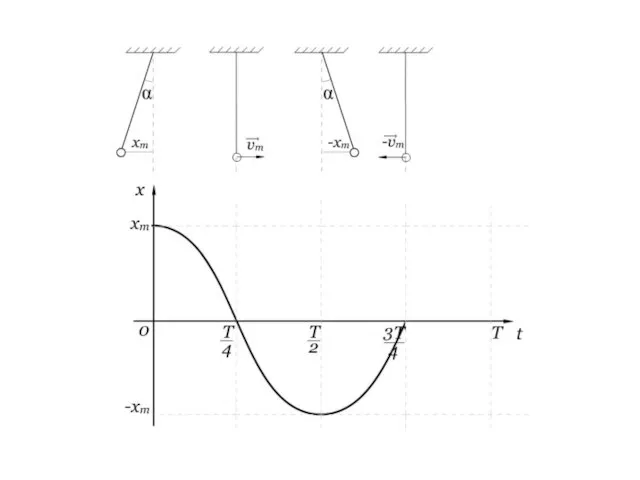
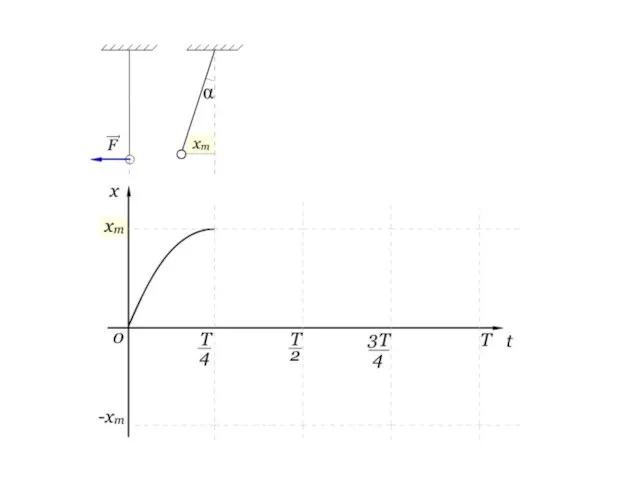
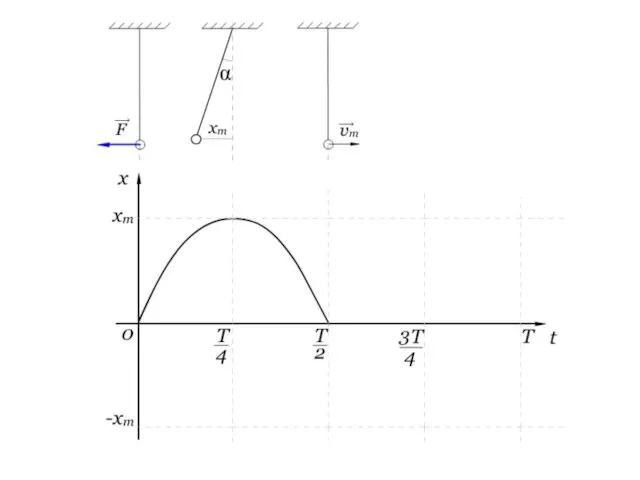
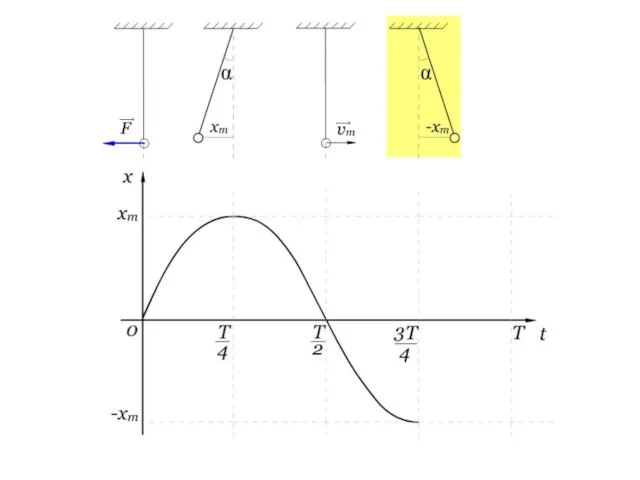
Выясним, как же зависит координата от времени
Рассмотрим пример

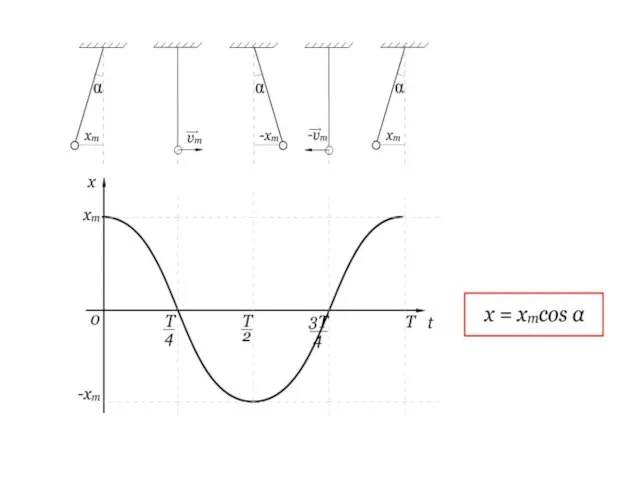
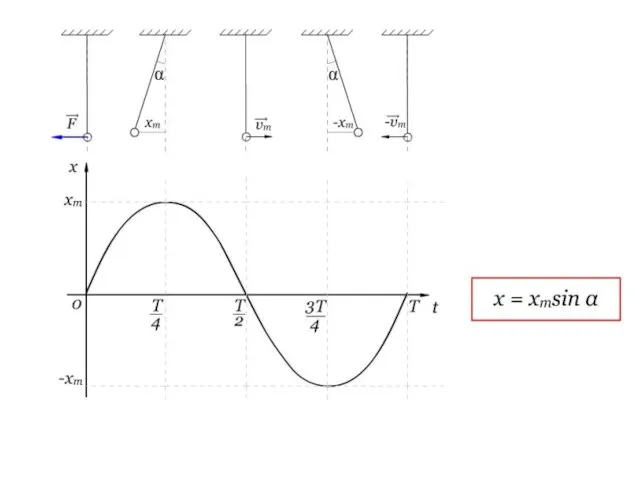
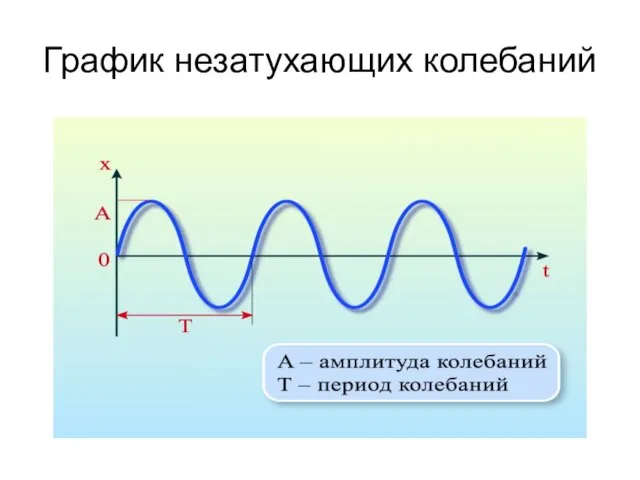
График незатухающих колебаний

Фаза колебаний
Фаза колебаний-φ (аргумент синуса или косинуса)-величина стоящая под знаком косинуса или синуса

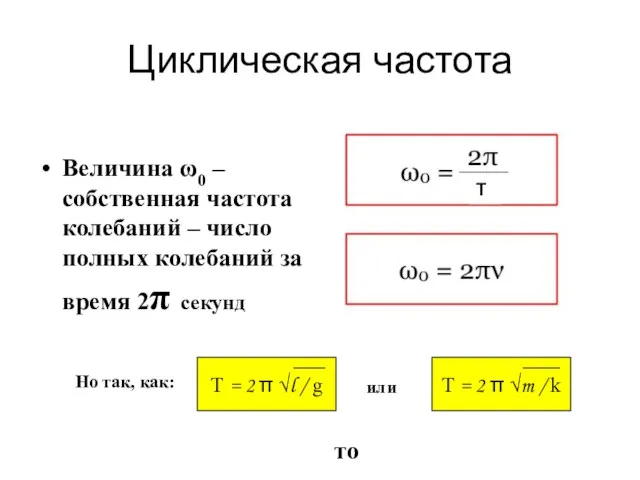
Циклическая частота
Величина ω0 – собственная частота колебаний – число полных колебаний за время 2π секунд
Т
Но так, как:
Т = 2 π √l / g
Т = 2 π √m / k
или
то

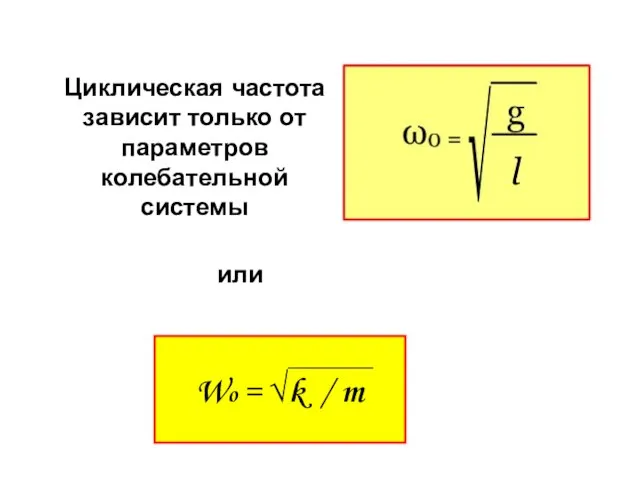
Циклическая частота зависит только от параметров колебательной системы
или
Wo = √k / m

Уравнение гармонических колебаний координаты

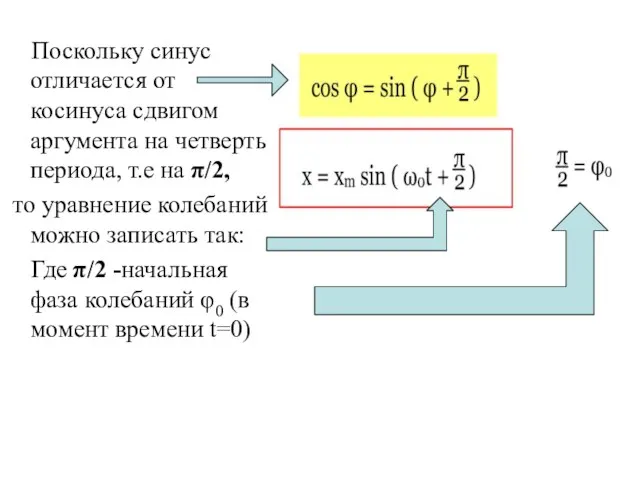
Поскольку синус отличается от косинуса сдвигом аргумента на четверть периода, т.е на π/2,
то уравнение колебаний можно записать так:
Где π/2 -начальная фаза колебаний φ0 (в момент времени t=0)

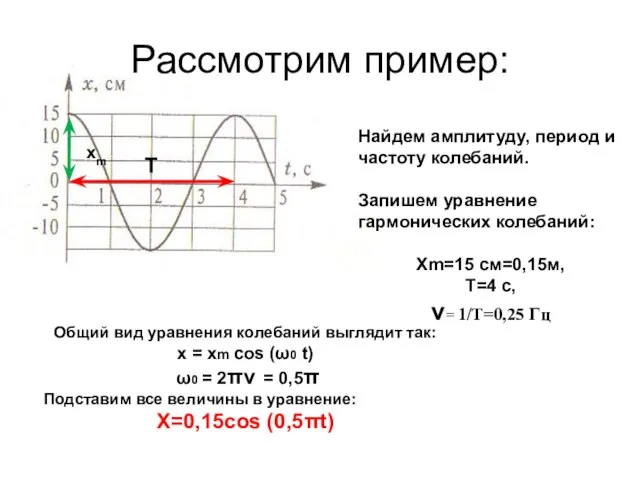
Рассмотрим пример:
Найдем амплитуду, период и частоту колебаний.
Запишем уравнение гармонических колебаний:
Хm=15 см=0,15м,
Т=4 с,
ν= 1/Т=0,25 Гц
Т
хm
Общий вид уравнения колебаний выглядит так:
х = хm cos (ω0 t)
ω0 = 2πν = 0,5π
Подставим все величины в уравнение:
X=0,15cos (0,5πt)

Домашнее задание
А)Прочитать §§ 26 - 27, выучить конспект
В)Ответить на 3,5 вопросы после § 27 письменно
С) Решить Упр 22 (4,5)
Д)Изучить описание лабораторной работы № 3
на стр 107 – 108.
Е) Ответить на вопросы:
1) Как изменится период математического маятника с железным шариком, если под ним поместить магнит?

Рассмотрим пример 1
А = 0,5 м
Х = А соs2πt/Т
2π/Т = π/2
Т = 4с

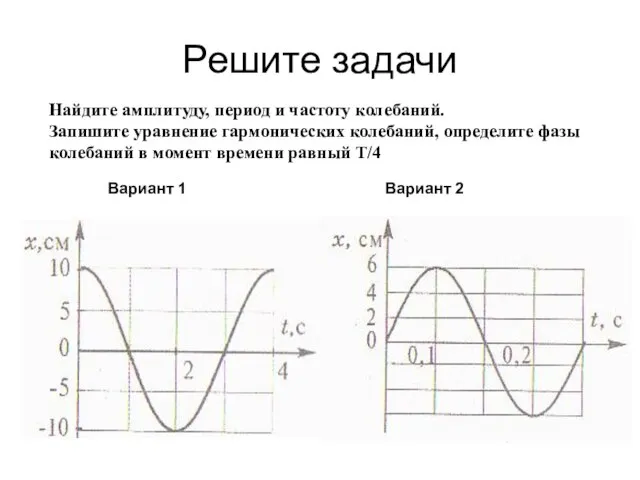
Решите задачи
Найдите амплитуду, период и частоту колебаний.
Запишите уравнение гармонических колебаний, определите фазы колебаний в момент времени равный Т/4
Вариант 1
Вариант 2