Содержание
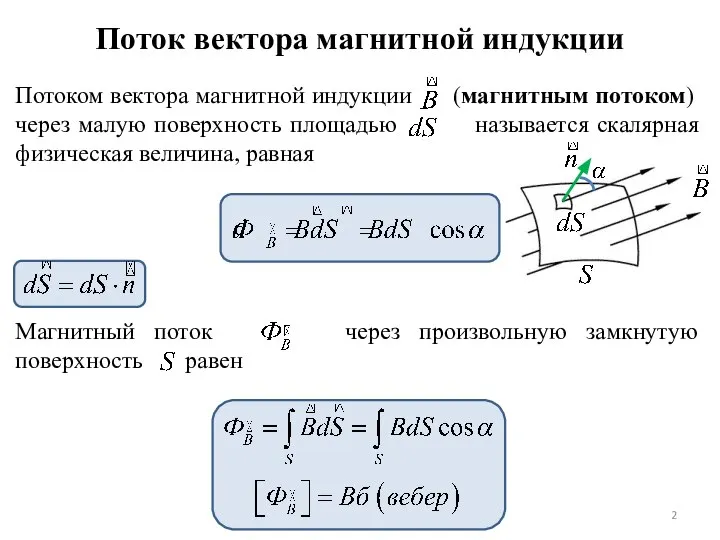
- 2. Поток вектора магнитной индукции Потоком вектора магнитной индукции (магнитным потоком) через малую поверхность площадью называется скалярная
- 3. Отсутствие в природе магнитных зарядов приводит к тому, что линии вектора не имеют ни начала, ни
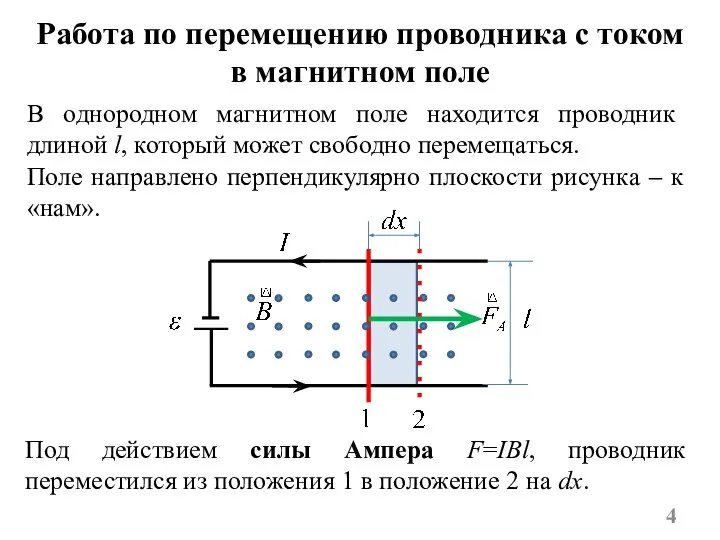
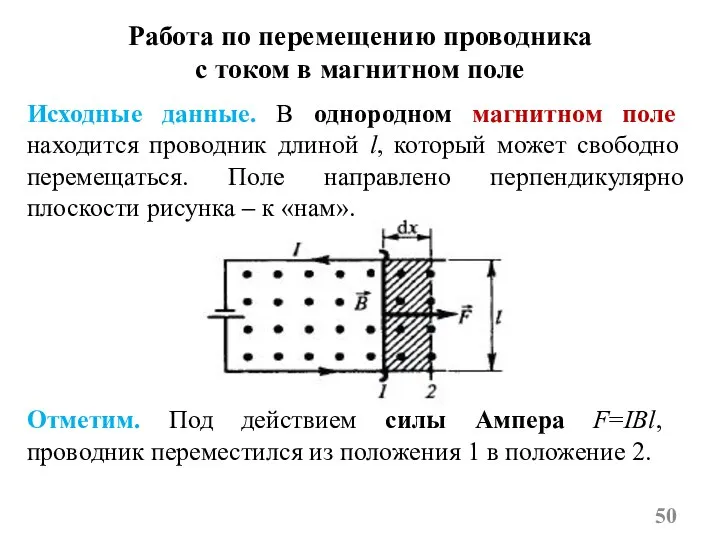
- 4. Работа по перемещению проводника с током в магнитном поле Под действием силы Ампера F=IBl, проводник переместился
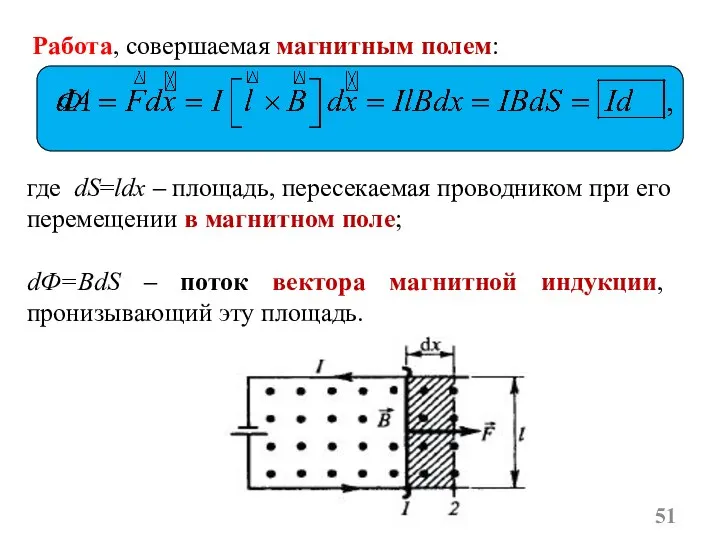
- 5. где dS=ldx – площадь, пересекаемая проводником при его перемещении в магнитном поле; dФ=BdS – поток вектора
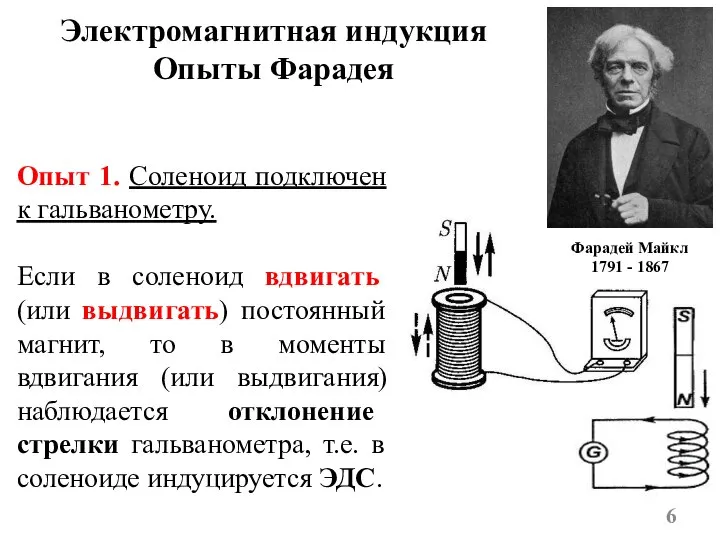
- 6. Электромагнитная индукция Опыты Фарадея Опыт 1. Соленоид подключен к гальванометру. Если в соленоид вдвигать (или выдвигать)
- 7. Направление отклонения стрелки при вдвигании и выдвигании противоположны. Если постоянный магнит развернуть так, чтобы полюса поменялись
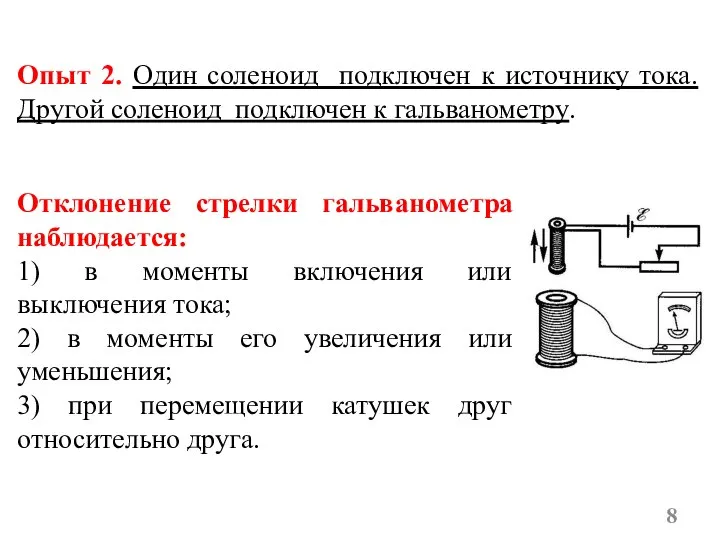
- 8. Отклонение стрелки гальванометра наблюдается: 1) в моменты включения или выключения тока; 2) в моменты его увеличения
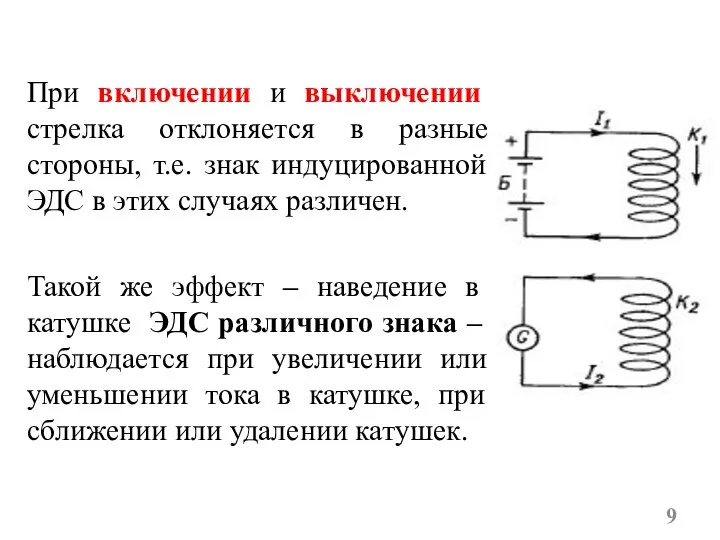
- 9. При включении и выключении стрелка отклоняется в разные стороны, т.е. знак индуцированной ЭДС в этих случаях
- 10. В опытах Фарадея было открыто явление электромагнитной индукции. В замкнутом проводящем контуре при изменении потока магнитной
- 11. Свойства индукционного тока Индукционный ток возникает всегда, когда происходит изменение сцепленного с контуром потока магнитной индукции.
- 12. Экспериментальные факты. В опытах Фарадея при любом изменении потока магнитной индукции, сцепленного с контуром, всегда возникал
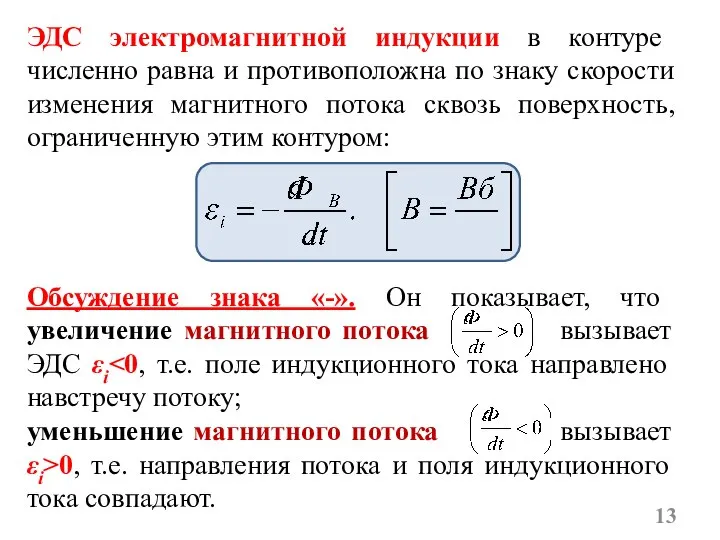
- 13. ЭДС электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь
- 14. Направление индукционного тока. Правило Ленца Индукционный ток в контуре всегда принимает такое направление, что созданное им
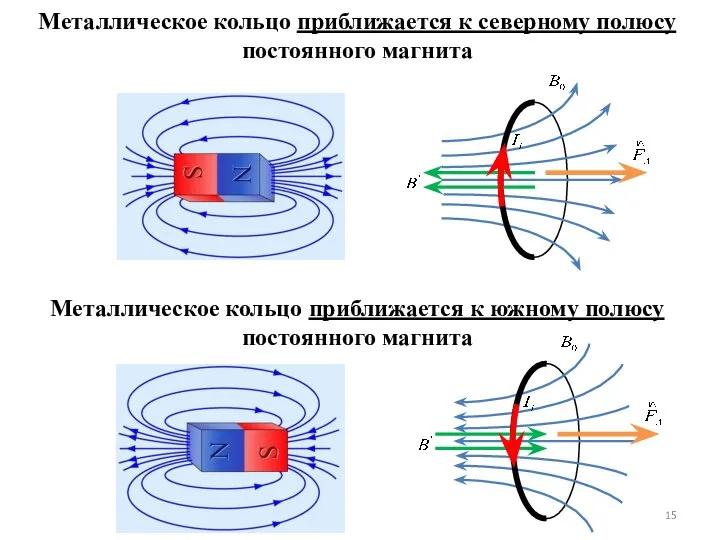
- 15. Металлическое кольцо приближается к северному полюсу постоянного магнита Металлическое кольцо приближается к южному полюсу постоянного магнита
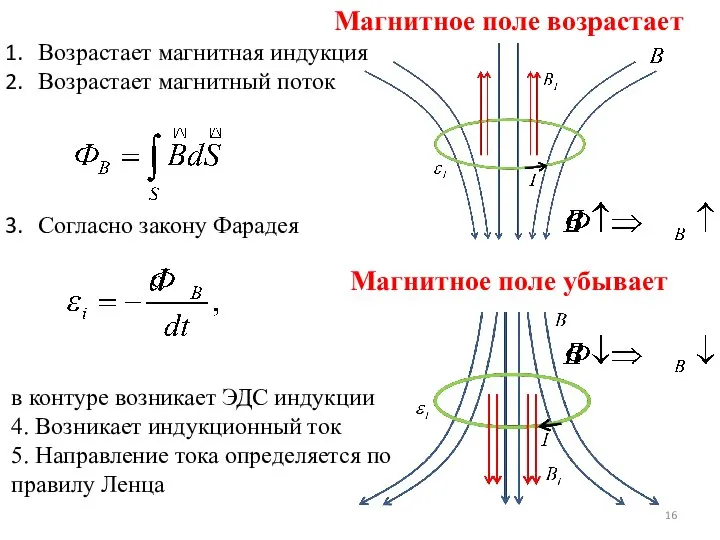
- 16. Магнитное поле возрастает Возрастает магнитная индукция Возрастает магнитный поток Согласно закону Фарадея в контуре возникает ЭДС
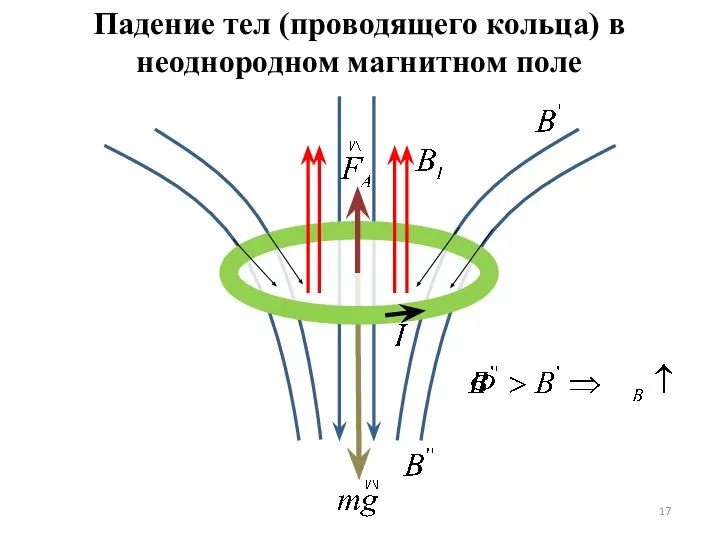
- 17. Падение тел (проводящего кольца) в неоднородном магнитном поле
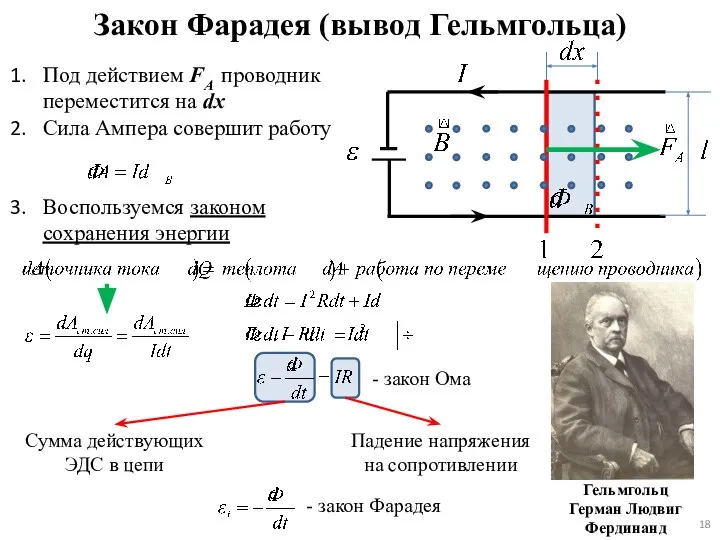
- 18. Закон Фарадея (вывод Гельмгольца) Под действием FA проводник переместится на dx Сила Ампера совершит работу Воспользуемся
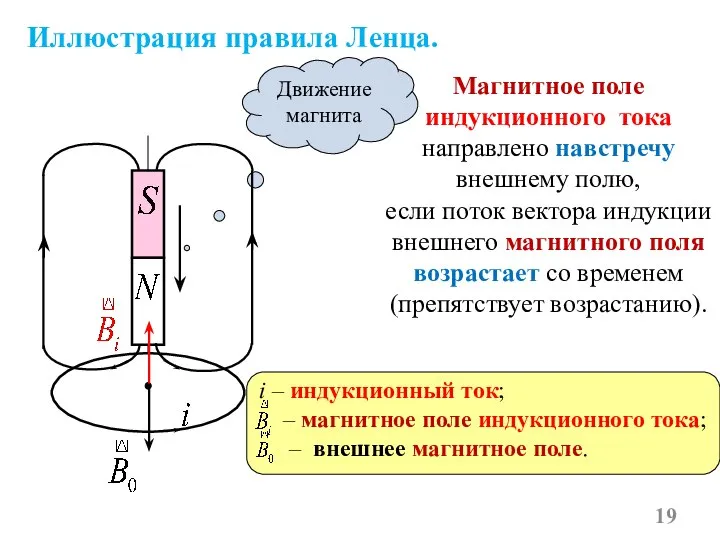
- 19. Иллюстрация правила Ленца. Магнитное поле индукционного тока направлено навстречу внешнему полю, если поток вектора индукции внешнего
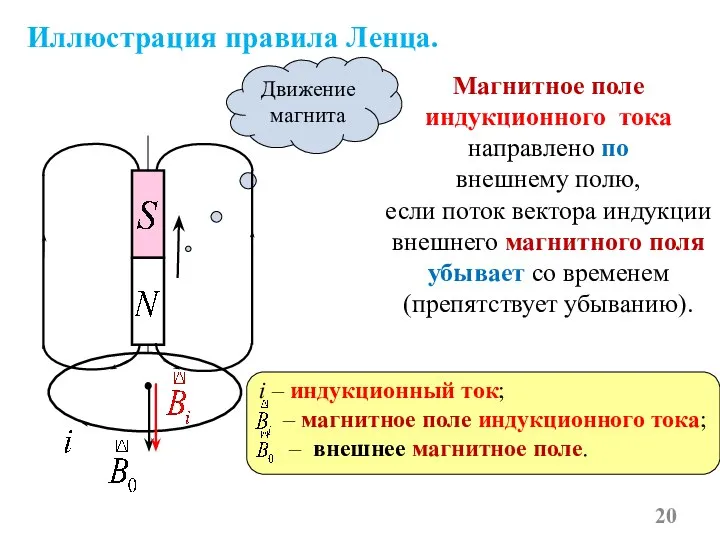
- 20. Иллюстрация правила Ленца. Магнитное поле индукционного тока направлено по внешнему полю, если поток вектора индукции внешнего
- 21. Вихревой ток - это индукционный ток, возникающий в массивных сплошных проводниках, помещенных в переменное магнитное поле.
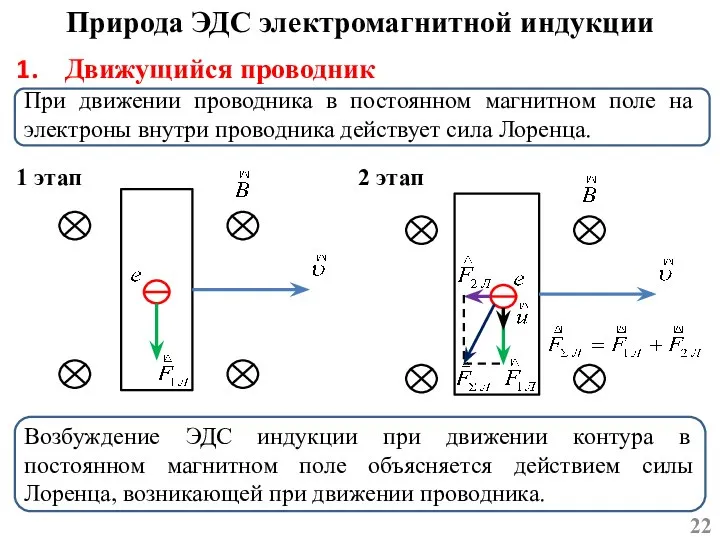
- 22. Движущийся проводник При движении проводника в постоянном магнитном поле на электроны внутри проводника действует сила Лоренца.
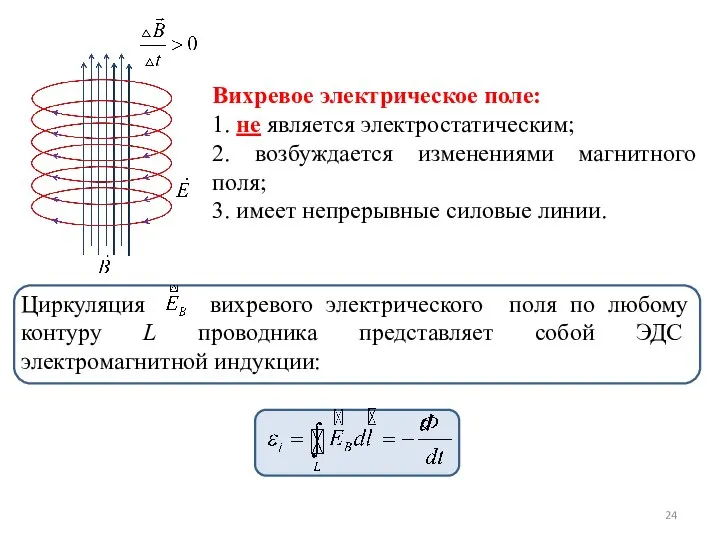
- 23. Переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле, которое и является причиной возникновения индукционного
- 24. Вихревое электрическое поле: 1. не является электростатическим; 2. возбуждается изменениями магнитного поля; 3. имеет непрерывные силовые
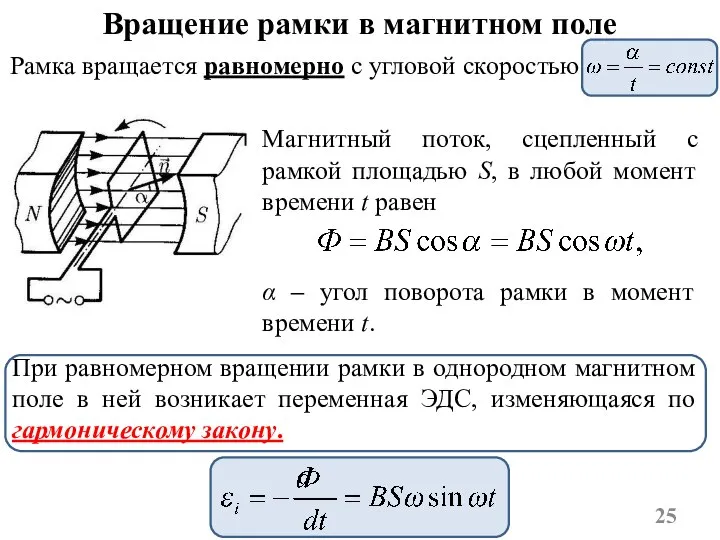
- 25. Рамка вращается равномерно с угловой скоростью Вращение рамки в магнитном поле Магнитный поток, сцепленный с рамкой
- 26. Электрический ток, текущий в замкнутом контуре, создаёт вокруг себя магнитное поле, индукция которого, по закону Био-Савара-Лапласа,
- 27. N – число витков соленоида, l – его длина, S – площадь, μ0 – магнитная постоянная,
- 28. Явление самоиндукции При изменении силы тока в контуре будет изменяться и сцепленный с ним магнитный поток,
- 29. ЭДС самоиндукции (закона Фарадея): Если контур не деформируется и магнитная проницаемость среды не изменяется, то L=const
- 30. Если ток со временем возрастает, то εs Если ток со временем убывает, то εs>0, т.е. ток
- 31. При замыкании цепи ЭДС самоиндукции вызывает ток, препятствующий увеличению основного тока в цепи, что делает конечной
- 32. Ток в цепи определяется законом Ома Разделяем переменные: и интегрируем по I (от I0 до I)
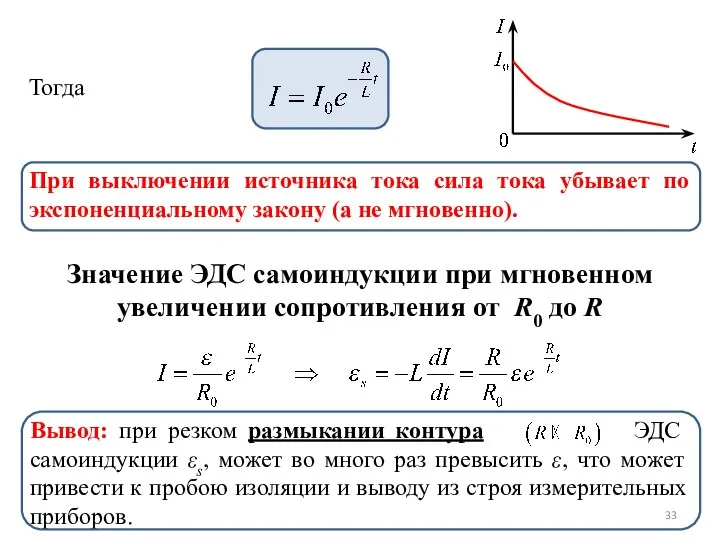
- 33. Тогда При выключении источника тока сила тока убывает по экспоненциальному закону (а не мгновенно). Значение ЭДС
- 34. При замыкании цепи помимо внешней ЭДС ε возникает ЭДС самоиндукции εs, препятствующая возрастанию тока. По закону
- 35. Взаимной индукцией называется явление возбуждения ЭДС электромагнитной индукции в одной электрической цепи при изменении электрического тока
- 36. Коэффициенты пропорциональности L21 и L12 равны друг L12=L21=L другу и называются взаимной индуктивностью контуров. При изменении
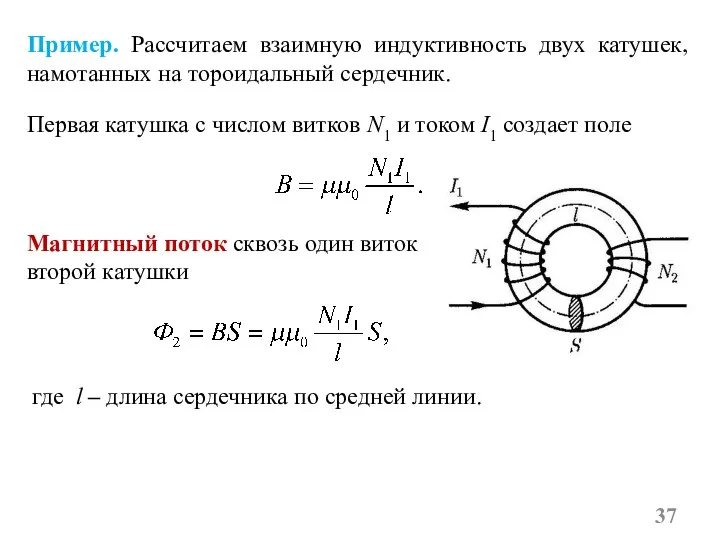
- 37. Пример. Рассчитаем взаимную индуктивность двух катушек, намотанных на тороидальный сердечник. Первая катушка с числом витков N1
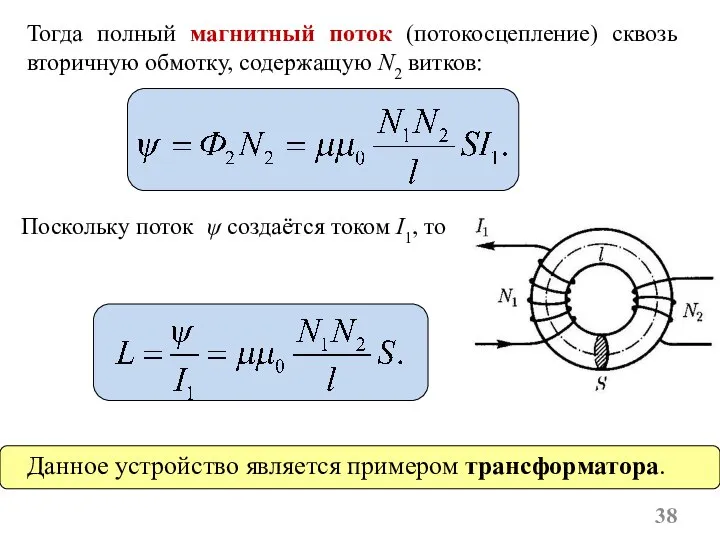
- 38. Поскольку поток ψ создаётся током I1, то Тогда полный магнитный поток (потокосцепление) сквозь вторичную обмотку, содержащую
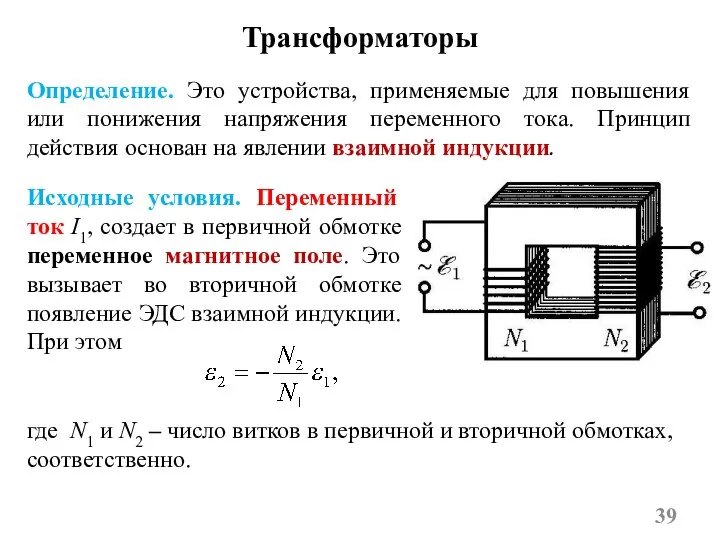
- 39. Определение. Это устройства, применяемые для повышения или понижения напряжения переменного тока. Принцип действия основан на явлении
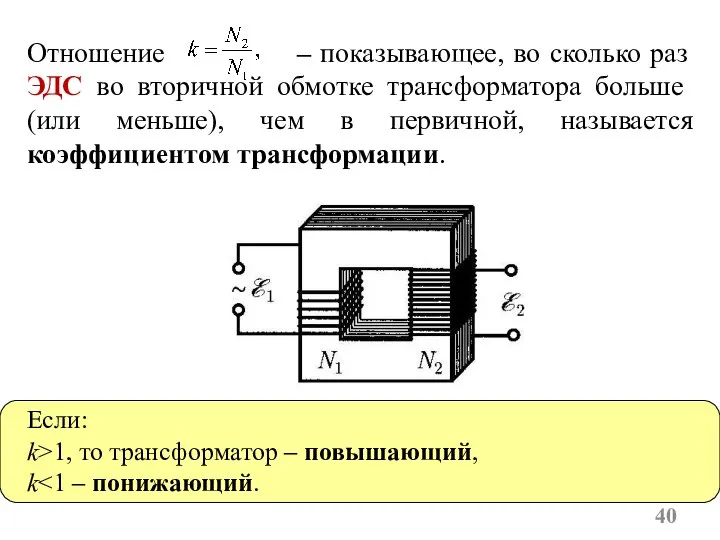
- 40. Отношение – показывающее, во сколько раз ЭДС во вторичной обмотке трансформатора больше (или меньше), чем в
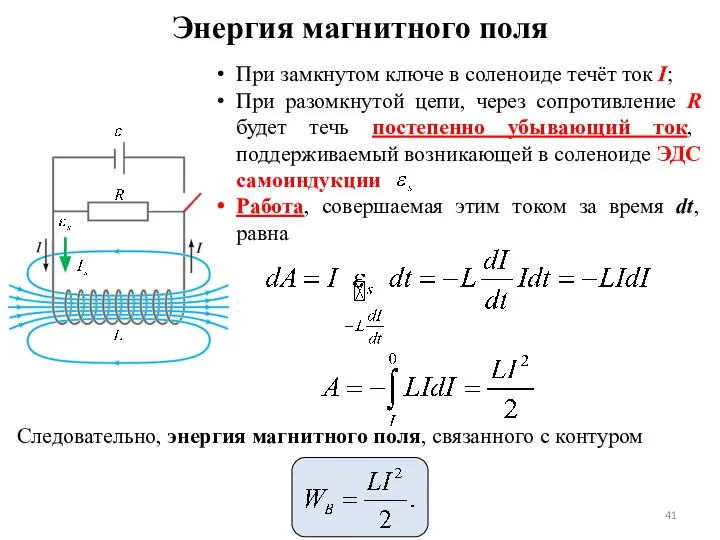
- 41. Энергия магнитного поля Следовательно, энергия магнитного поля, связанного с контуром
- 42. Исходные условия. Рассчитаем магнитное поле длинного соленоида, используя уже известные формулы: Используя эти соотношения, получим где
- 43. Магнитное поле длинного соленоида однородно и сосредоточено внутри него, поэтому энергия заключена в объеме соленоида и
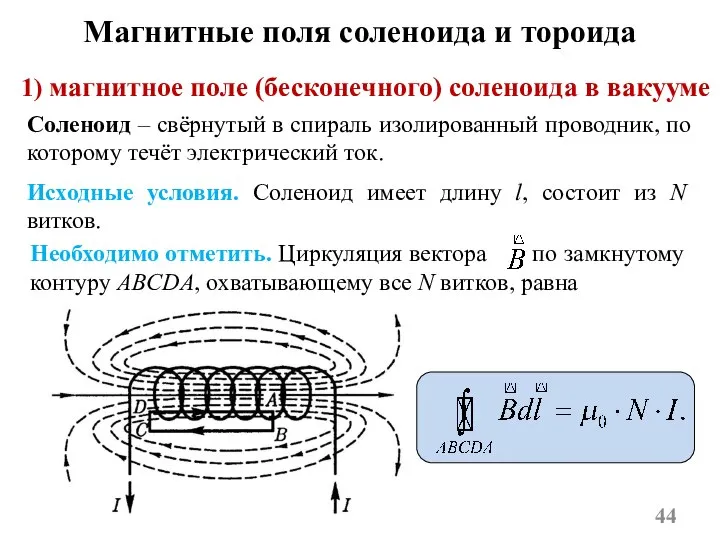
- 44. 1) магнитное поле (бесконечного) соленоида в вакууме Соленоид – свёрнутый в спираль изолированный проводник, по которому
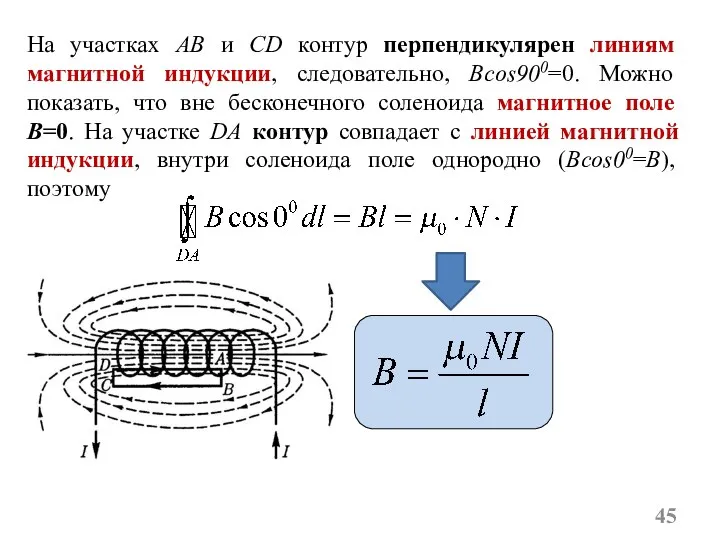
- 45. На участках AB и CD контур перпендикулярен линиям магнитной индукции, следовательно, Bcos900=0. Можно показать, что вне
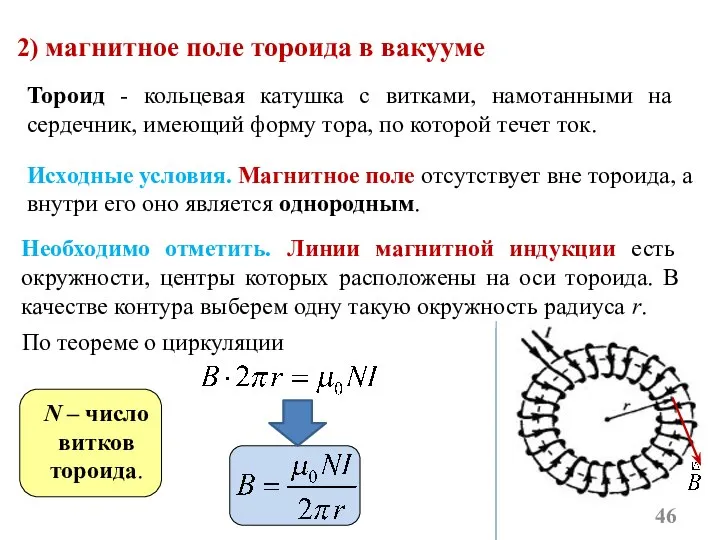
- 46. 2) магнитное поле тороида в вакууме Тороид - кольцевая катушка с витками, намотанными на сердечник, имеющий
- 47. Поток вектора магнитной индукции (магнитный поток) через площадку dS – СФВ, равная где α – угол
- 48. Поток вектора связывают с контуром, по которому течет ток. Положительное направление нормали к контуру связано с
- 49. Теорема Гаусса для магнитного поля в вакууме: поток вектора магнитной индукции сквозь любую замкнутую поверхность S
- 50. Работа по перемещению проводника с током в магнитном поле Отметим. Под действием силы Ампера F=IBl, проводник
- 51. где dS=ldx – площадь, пересекаемая проводником при его перемещении в магнитном поле; dФ=BdS – поток вектора
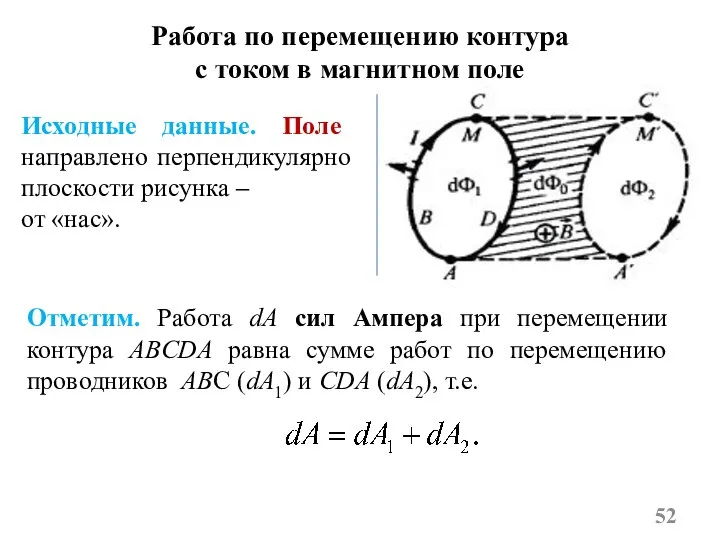
- 52. Работа по перемещению контура с током в магнитном поле Отметим. Работа dA сил Ампера при перемещении
- 53. Особенно важно. 1) При перемещении участка CDA силы Ампера направлены в сторону перемещения (образуют с направлением
- 54. В сумме Работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока
- 56. Скачать презентацию


























 Основное уравнение динамики вращательного движения твердого тела. (Лекция 7)
Основное уравнение динамики вращательного движения твердого тела. (Лекция 7) Видатні вчені фізики
Видатні вчені фізики Температура. Виды термометров
Температура. Виды термометров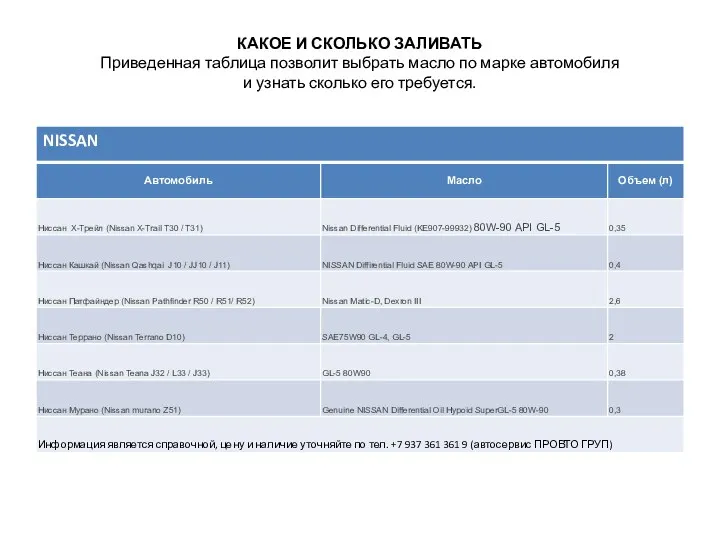 Объем заправочных масел
Объем заправочных масел Тепловые процессы: нагревание, охлаждение, конденсация и выпаривание
Тепловые процессы: нагревание, охлаждение, конденсация и выпаривание Маса. інертність
Маса. інертність Выталкивающая сила. Закон Архимеда
Выталкивающая сила. Закон Архимеда Презентация на тему Ультрафиолетовые лучи
Презентация на тему Ультрафиолетовые лучи  ВКР: Совершенствование системы ТО с разработкой приспособления для обслуживания тормозной системы
ВКР: Совершенствование системы ТО с разработкой приспособления для обслуживания тормозной системы Курс лекций по молекулярной физике и термодинамике
Курс лекций по молекулярной физике и термодинамике Аэродинамика
Аэродинамика Методологические основы и структура научного познания. Лекция №1
Методологические основы и структура научного познания. Лекция №1 Поля и взаимодействия. Лекция 01. Введение
Поля и взаимодействия. Лекция 01. Введение Гамма излучение
Гамма излучение Распространение радиоволн
Распространение радиоволн Электростатика. Электродинамика
Электростатика. Электродинамика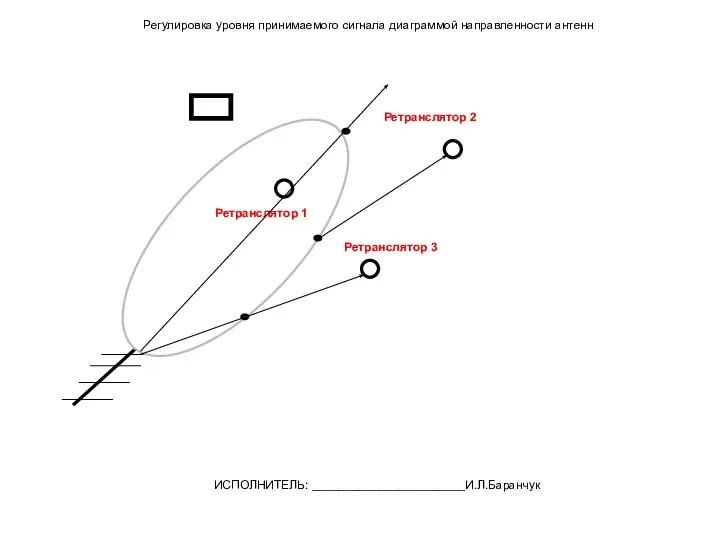 Регулировка уровня принимаемого сигнала диаграммой направленности антенн
Регулировка уровня принимаемого сигнала диаграммой направленности антенн Электромагнитные явления
Электромагнитные явления Звуковые волны. Свойства звука
Звуковые волны. Свойства звука Нерезьбовые соединения. Шпоночное соединение
Нерезьбовые соединения. Шпоночное соединение Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения. Развитие ядерной энергетики
Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения. Развитие ядерной энергетики Распределение скоростей течения в речном потоке
Распределение скоростей течения в речном потоке Изучение магнитооптической дифракции в пленках ферритов-гранатов
Изучение магнитооптической дифракции в пленках ферритов-гранатов Приймачі світла
Приймачі світла Ток, протекающий в нейтралях трансформаторов и автотрансформаторов при КЗ на землю
Ток, протекающий в нейтралях трансформаторов и автотрансформаторов при КЗ на землю Физические основы механики. Лекция 1.1
Физические основы механики. Лекция 1.1 Курвиметр. Велокомпьютер с цифровым одометром
Курвиметр. Велокомпьютер с цифровым одометром 3. Работа и энергия
3. Работа и энергия