Содержание
- 2. де Бройль (1924): материя так же, как и электромагнитное излучение, может одновременно проявлять свойства частицы и
- 3. Любой частице с импульсом p ставится в соответствие волновой процесс длина волны де Бройля Вывод: Корпускулярно-волновой
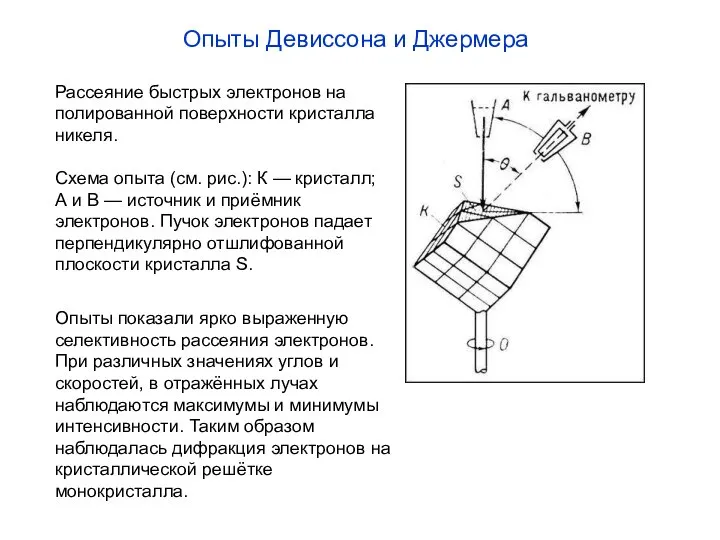
- 4. Опыты Девиссона и Джермера Рассеяние быстрых электронов на полированной поверхности кристалла никеля. Схема опыта (см. рис.):
- 5. Свойства волн де Бройля 1) Фазовая скорость волн де Бройля больше скорости света в вакууме. 2)
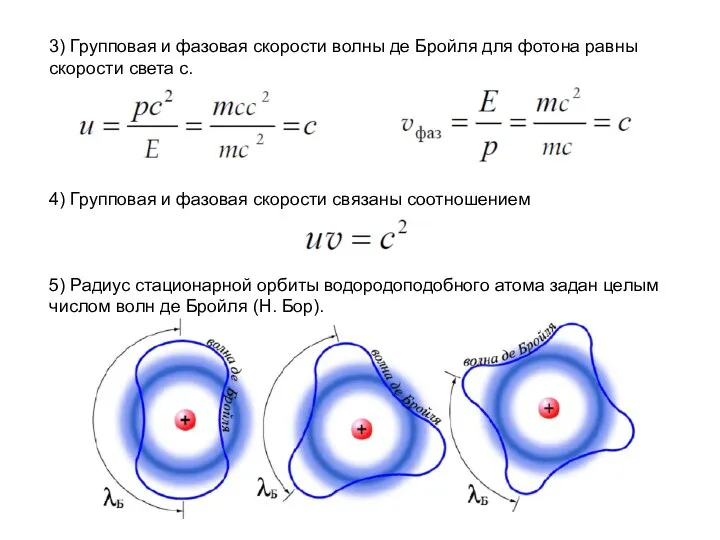
- 6. 3) Групповая и фазовая скорости волны де Бройля для фотона равны скорости света c. 4) Групповая
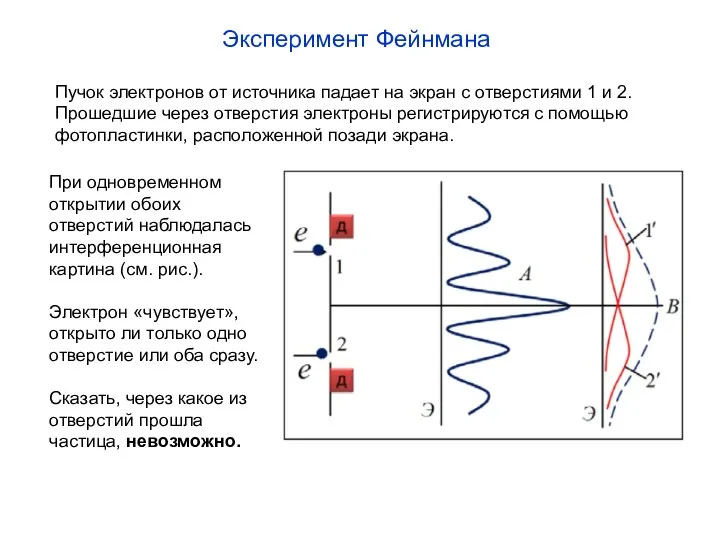
- 7. Эксперимент Фейнмана Пучок электронов от источника падает на экран с отверстиями 1 и 2. Прошедшие через
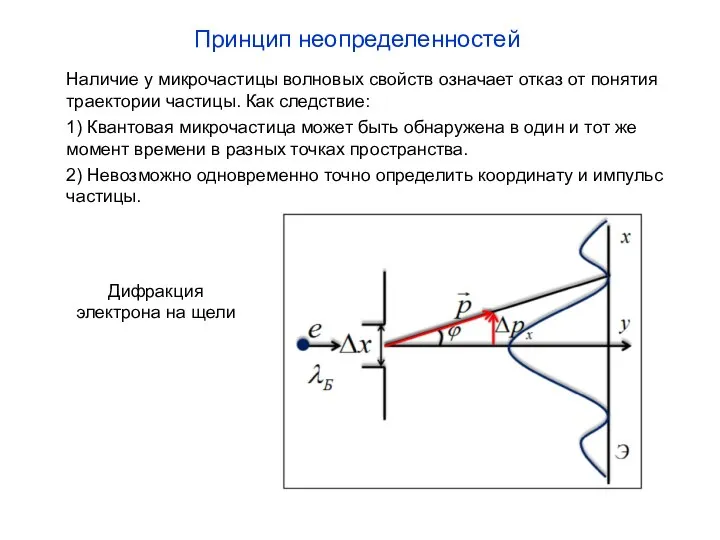
- 8. Наличие у микрочастицы волновых свойств означает отказ от понятия траектории частицы. Как следствие: 1) Квантовая микрочастица
- 9. Соотношение неопределенностей. 1) Неопределенности координаты и импульса до прохождения щели 2) ... после прохождения щели 3)
- 10. Таким образом, чем точнее мы определяем координату частицы, тем менее определенной становится проекция импульса частицы на
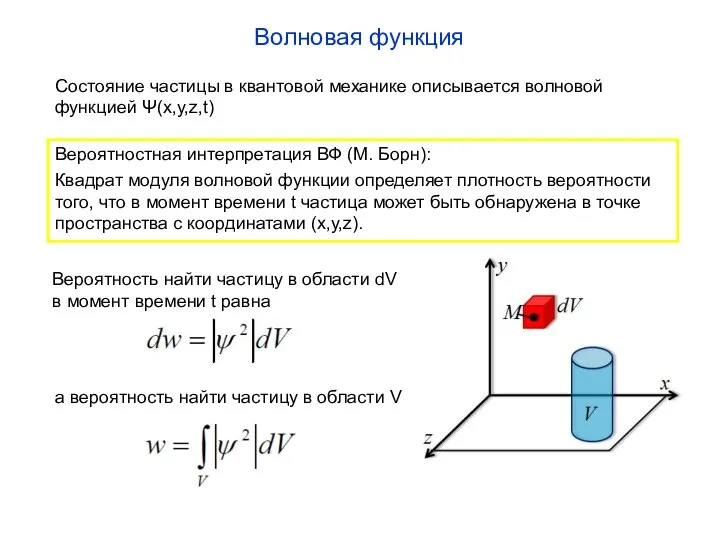
- 11. Волновая функция Состояние частицы в квантовой механике описывается волновой функцией Ψ(x,y,z,t) Вероятностная интерпретация ВФ (М. Борн):
- 12. Свойства волновой функции 1) Волновая функция должна удовлетворять условию нормировки. 2) Волновая функция должна быть: а)
- 14. Скачать презентацию






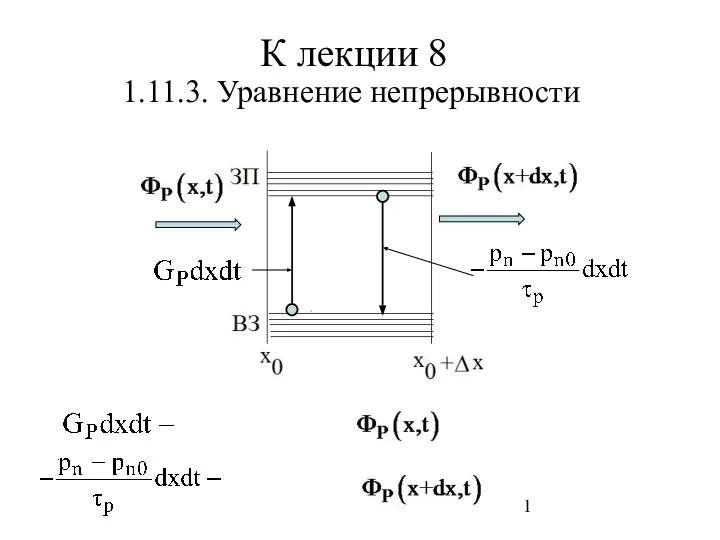 Уравнение непрерывности
Уравнение непрерывности Оценка прочности корпуса компрессора ГТД при ударе оторвавшейся лопатки
Оценка прочности корпуса компрессора ГТД при ударе оторвавшейся лопатки Механическая работа и мощность
Механическая работа и мощность Роль физико-химических методов анализа потребительских товаров при установлении их безопасности и качества
Роль физико-химических методов анализа потребительских товаров при установлении их безопасности и качества Аналогово-цифровой контроллер
Аналогово-цифровой контроллер Численные методы и оптимизация траекторий межпланетных траекторий
Численные методы и оптимизация траекторий межпланетных траекторий Температурные напряжения
Температурные напряжения 4. Основы МКТ
4. Основы МКТ Закон падения
Закон падения Рычаги. Кривошипно-ползунный механизм
Рычаги. Кривошипно-ползунный механизм Периодическое движение. Вращение. Колебание
Периодическое движение. Вращение. Колебание Кроссворд
Кроссворд Работа силы
Работа силы Закон Ома для участка цепи
Закон Ома для участка цепи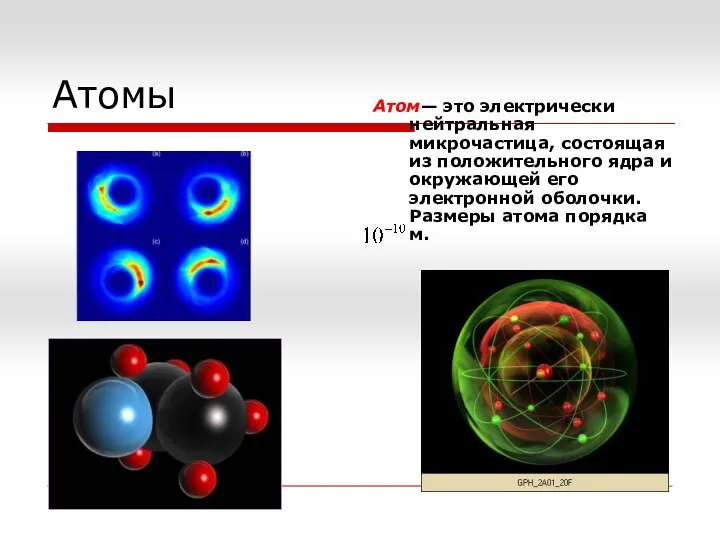 Атомы
Атомы Элементы квантовой механики
Элементы квантовой механики Блок контроля
Блок контроля Флюксметр (Веберметр)
Флюксметр (Веберметр) Радиация вокруг нас
Радиация вокруг нас Марковские процессы. Правило
Марковские процессы. Правило Посадочный размер блока. Диаметр ТЭНа
Посадочный размер блока. Диаметр ТЭНа Курс лекций по теоретической механике. Статика
Курс лекций по теоретической механике. Статика Нетрадиционная энергетика
Нетрадиционная энергетика Обеспечение высокого уровня технического обслуживания и текущего ремонта грузового транспорта в условиях предприятия
Обеспечение высокого уровня технического обслуживания и текущего ремонта грузового транспорта в условиях предприятия Повторение
Повторение Радиоактивность. Виды радиоактивного облучения
Радиоактивность. Виды радиоактивного облучения 10_ ОТС_ Методы анализа ЛИС-цепей 14
10_ ОТС_ Методы анализа ЛИС-цепей 14 Магнитная индукция
Магнитная индукция